同震地表破裂带空间分布形态的自动无损测量

邓德贝尔 刘小利 高天琪 乐子扬

1 中国地震局地震研究所，武汉市洪山侧路40号，430071 2 防灾科技学院，河北省三河市学院街465号，065201

地震地表破裂带包含了重要的几何结构关系，其几何形态、同震变形及其在空间上的分布特征是理解大陆地壳变形模式和地震破裂行为的关键[1-5]，也是构造活动区各种重要基础设施抗震设防的依据[6-8]。已有学者根据历史震例统计规律建立了同震地表位错与震级大小之间的函数映射关系，称之为地震危险性概率模型[6-7,9]，用于活动断层避让带的限定。但目前对同震地表破裂带宽度及其影响因素缺少足够的关注，不仅影响对地震破裂行为的全面认识，还制约了活动断层工程避让带宽度及其边界的准确限定[10]。

活动断层避让带宽度的测定方法主要有2种：跨断层地质探槽剖面分析法和同震地表破裂带宽度统计法[11]。前者需要实地开挖探槽，价格昂贵，一般适用于工地建设的精细探测；后者则是在震后应急调查中通过实地抽样调查和测量，获得主破裂断层沿线若干点位处破裂带宽度测量值，经过空间插值拟合得到整条破裂带的宽度分布。随着亚m级甚至cm级高空间分辨遥感技术在地震地质调查中的应用，快速获得大空间范围、详尽的、精细的同震地表破裂信息成为可能，以往地面调查难以覆盖到的地表破裂或现场肉眼易忽略的微弱地表裂缝可被再现[12]，通过室内精细解译和填图即可获得空间上几乎连续的同震地表破裂的分布形态。

为高效、精细地测量、统计和分析大量同震地表破裂数据，本文设计并实现了同震地表破裂空间分布形态的无损测量方法和基于Python平台的自动测量工具，并以2021年玛多MW7.4地震和1983年Idaho Lost River MW6.9地震数据进行性能测试，验证该方法的可信度和运算效率。

1 同震地表破裂带分布形态的无损测量方法

已有研究认为，地震地表破裂带一般由一系列性质不同的次级斜列断层、鼓包、裂缝、沟槽等组合而成[1,13]。目前，地表破裂带宽度主要指集中在发震断层上的同震地表破裂在断层正交方向上的延展宽度[13]，根据测量对象的空间尺度不同，又可分为单条地表破裂宽度和地表破裂带组合宽度。

准确限定同震地表破裂带的几何学宽度并不容易。在野外现场调查中，一般沿主破裂断层走向每间隔一定距离抽样测量一个破裂宽度值作为该段落地表破裂带的宽度。如图1，该段破裂带总体上沿aa′展布，走向大致为NEE，长约1 km，由多支近平行或小角度斜交的斜列式张剪性破裂组成。在实地调查中，首先根据破裂的延展性、规模大小和总体走向，确定主破裂位置作为基准，测量其正交方向bb′两侧破裂的最远位置，作为测量点处地表破裂带的宽度值。例如，在P1点的测量值为48 m，作为该点两侧一定范围(P1点处阴影区)的破裂带宽度值，但该点东南侧A区仍有地表破裂未被覆盖；P2点的测量值为166 m，但该点东南侧B区较大范围内没有地表破裂。可见，在不同位置上抽样测量所获得的测量值往往会偏大或偏小，具有较大的不确定性。

此外，当地表破裂分布在数百米甚至更宽的范围时，由于现场观测视野的局限性或者距离主破裂较远处次级破裂规模较小、变形微弱而被忽视(P1点南侧的C、D区域)，使得部分破裂未被纳入测量范围，进而导致破裂带宽度被低估[12]。从统计意义上来说，应量取测量点位处包含所有地表破裂的最大垂向距离作为该点位地表破裂带的宽度。以图1为例，A区、C区代表不同规模的破裂迹线，将A区、C区及中间空白区域合并测量，得到该段破裂带的总体宽度。

基于上述分析，为客观、真实地再现同震地表破裂带的空间分布形态，满足不同研究的差异性需要，本文提出一种无损失逐点扫描、变尺度统计的测量方法，即以主破裂断层为基准线，由一端向另一端等间隔移动扫描与主破裂断层正交方向上两侧破裂的最大垂向距离，作为该测量点位破裂带的最远包络形迹点，所有测量点位处的最远包络形迹点即可形成地表破裂带的包络多边形，测量点位到主破裂断层起始端点的长度即为测量点到主断层起始端点的实际距离。因此，地表破裂空间分布形态的测量过程，就是绘制地表破裂包络多边形的过程，也是将空间坐标系统转换到以主破裂断层走向方向及其正交方向为基准坐标轴的投影转换过程。

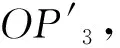
显然，该包络多边形的精度取决于原始数据的分辨精度和测量密度，因此沿主破裂断层扫描时，必须以最高分辨率设置移动窗口尺寸才能实现无损测量。在此基础上，取移动窗口尺寸的任意倍数对数据进行最值、中位数、平均值等统计分析或制图，满足变尺度研究需要。

2 算法设计与实现

基于上述无损测量方法，设计并实现了相应的自动无损测量和变尺度统计算法，详细流程见图2。

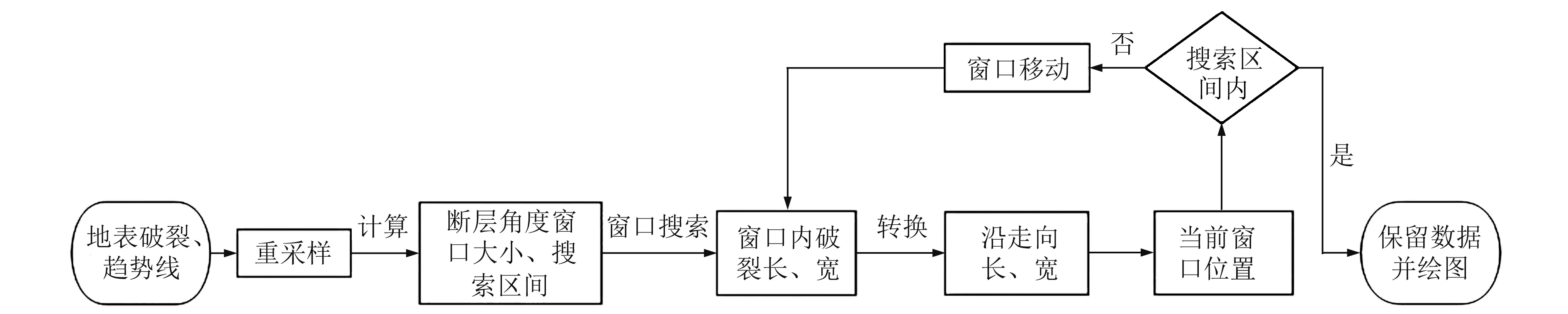
图2 算法流程Fig.2 Algorithm flow chart

1)数据重采样。将地表破裂线、主破裂断层线文件按最高分辨率大小离散为点文件，以实现无损转换与测量。如基于5 cm像素分辨率的航空影像获得同震地表破裂信息，其最小分辨能力即为5 cm，将破裂线离散为间隔5 cm的一组点，可无损地再现原始数据包含的破裂信息。线文件可以是地理投影或平面投影，算法自动检测并转换为平面投影坐标。

2)求包络形迹点。以主破裂断层为基准线，设置搜索窗口(图1中E区)，调节窗口步长(scale)，等间隔扫描主断层正交方向两侧最远的点。此时，需要根据主断层的走向(式(1))确定其正交方向，并进行包络形迹点的判定。假设A、B两点为主断层上测量点位两侧相邻的点，这两点间地理方位角即为该测量点处断层的走向值(α)：

(1)

式中，y为纬度，x为经度。

3)计算宽度。以测量点位主断层走向为依据进行正交方向的限定，主断层两侧包络形迹点到主断层的垂向距离即为该点处主断层两盘地表破裂的宽度，两盘宽度之和即为该点处地表破裂带总体宽度。当地表破裂带存在空区(部分段落没有破裂)时，程序会给定宽度值为0。此外，程序还允许以震中为水平距离零点位置，仅需调整起始端点的距离参数值即可。

4)统计分析与平滑。基于无损测量值，可根据实际需要灵活选择分析窗口尺寸(如原始数据分辨率或其任意倍数)，进行最值、中位数、平均数等统计分析或变尺度平滑处理。

基于上述步骤获得的结果，可进一步展示破裂带的可视化空间分布形态。基于Paython的shapefile、pandas、scipy、matplotlib等工具包实现该算法。

3 算法测试与震例分析

3.1 实验数据

为测试算法的可靠性和运算效率，分别选取1983年Idaho Lost River MW6.9地震[14]和2021年青海玛多MW7.4地震的同震地表破裂数据进行实验。

3.2 可靠性分析

3.2.1 Idaho Lost River地震

如图3所示，基于文献[15]提供的1983年Idaho Lost River MW6.9地震空间最小单元为1 m的地表破裂数据，测量窗口分别设置为1 km、100 m、1 m，获得的地表破裂带宽度变化特征见图4。

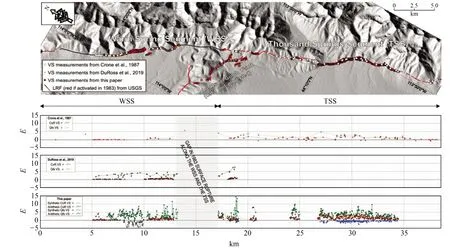
图3 文献[15]选用的断层及宽度(WGS 1984 UTM Zone 12N坐标系)Fig.3 Fault and width used in the literature[15](WGS 1984 UTM Zone 12N coordinates)

图4显示，测量窗口为100 m或1 m时，测量结果几乎一致，但前者耗时更少；当测量窗口大于1 km时，测量结果失真较为严重。图3中，8～12 km区间，地表破裂带宽度达到第1个峰值，约为6～7 km；17～18 km区间，地表破裂带宽度达到第2个峰值，约为5～6 km；27～34 km区间，地表破裂带集中分布于3～5 km范围内；13～17 km区间为一段空区，表示该区间没有地表破裂。图4对应位置测量值的整体趋势与图3结果一致，展现了地表破裂沿主断层走向变化的更多细节和总体宽度变化。值得注意的是，在8～12 km区间出现的最大峰值并不代表在6～7 km范围内广泛分布着同震地表破裂。结合地表破裂的空间分布(图3)，此处存在两支斜交的同震地表破裂带，使破裂带整体宽度较大。

图4 地表破裂空间分布形态Fig.4 Spatial distribution pattern of surface rupture

3.2.2 玛多震例

为进一步考察数据分辨率对测量结果的影响，选择2021年玛多MW7.4地震空间最小单元为3 cm的地表破裂数据，并根据光学遥感影像解译和D-InSAR反演形变场指示的发震断层[12]勾绘主破裂断层趋势线进行测试。如图5所示，该段地表破裂由北(AB)、南(CD)两支破裂带组成。为无损失地保留原始数据的精度，线文件离散为点文件时，以原始数据分辨率(3 cm)作为移动窗口的尺寸。如前文所述，趋势线的选取(大致沿破裂带整体走向)对破裂带整体分布宽度的量取影响较小，但会影响两侧破裂带分布宽度的测量结果。如果将图5中所有地表破裂基于AB或CD任意一条趋势线进行处理，其结果都无法准确表征破裂带的细节特征。因此，当破裂分叉时，需要对破裂分支分别进行趋势线拟合，分支破裂分别拟合时的分布形态结果见图6(a)和6(b)，整条破裂带的分布形态见图6(c)。

图5 分支破裂Fig.5 Branch rupture

图6 破裂分布形态Fig.6 Rupture distribution pattern

图6(a)中，AB段破裂西侧的宽度明显大于东侧；以趋势线为参考，其北侧地表破裂宽度明显小于南侧，很好地展示了图5中AB、CD段破裂的空间分布形态。图5中地表破裂仅基于AB或CD任意一条趋势线处理，会对C～B区间大片空白区域进行计算，造成较大的测量误差。显然，该震例中同震地表破裂空间分布形态的无损测量是基于原始数据的分辨率来完成的，数据分辨率越高，测量结果越精细，可反映的破裂细节特征越多。

3.3 运算效率测试

为测试算法的运算性能，选取玛多地震一段长约1 km的地表破裂进行实验(图1)，其空间分辨率为3 cm，密集分布了约3 900条破裂线，累积长度约为5.95 km，离散后点集数达1.98×105个，按不同测量窗口(3 cm、10 cm、50 cm、1 m、5 m、10 m)进行线转点离散化、宽度计算、平滑及绘图测试，耗时结果见图7。可以看出，算法耗时主要取决于宽度计算。随着数据分辨率的降低，时间消耗大致呈下降趋势，但因数据分辨率不同而引起的宽度耗时差别不明显。在实际应用中，可根据对数据精细程度的要求在不同阶段选择合适的处理尺度。

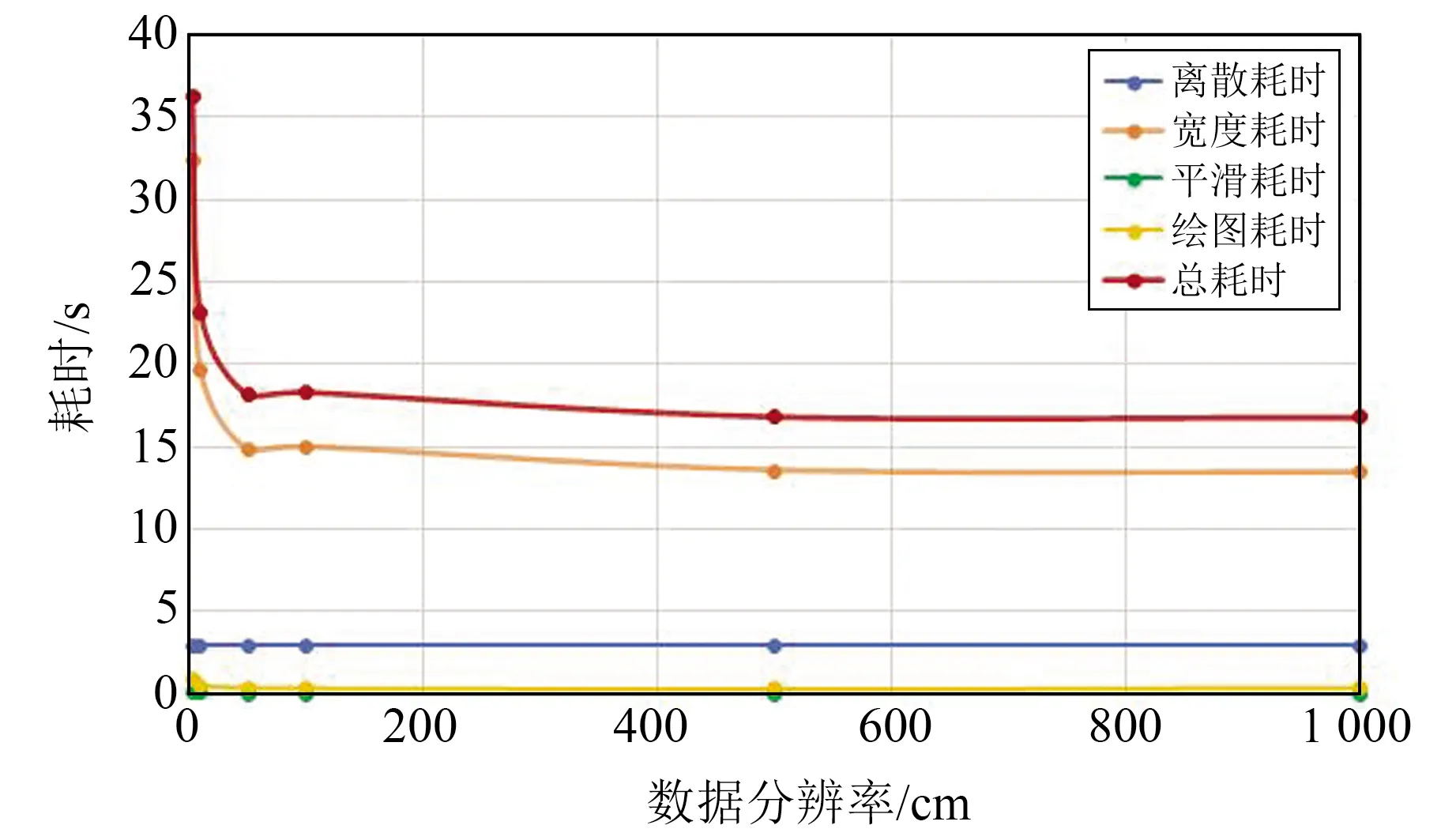
图7 耗时结果Fig.7 Time consuming results

图8为利用不同大小测量窗口得到的地表破裂空间分布形态。可以看出，随着测量窗口尺度的增大，地表破裂空间形态变得愈加平滑，部分细节特征丢失，破裂带宽度的离散程度逐渐减小，尤其是当测量窗口大于5 m时，破裂带离散程度趋于稳定；当测量窗口在5～50 m时，测量宽度变化显著，特征仍有保留；当测量窗口超过150 m时，测量特征大量丢失。

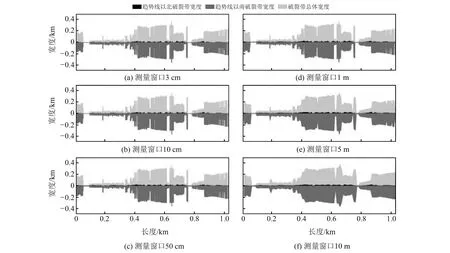
图8 不同大小测量窗口对应的地表破裂空间分布形态Fig.8 Spatial distribution pattern of surface rupture corresponding to different measurement windows

较高的数据分辨率可缓解测量窗口选取对测量结果的干扰，但随着数据分辨率的增加，数据量也越大，处理耗时越高。破裂趋势线是基于地表破裂的整体趋势确定的，实际上其走向变化频率远小于破裂线文件的最高分辨率精度。此外，根据破裂趋势线的方向确定各个测量点位处正交方向的过程耗时最高。因此，基于相同的数据集，可根据实际需要设置不同的测量窗口因子，以窗口内破裂宽度的某一统计数值表示该区域破裂宽度，近似获取整条破裂带宽度的测量结果。总之，对于精细的地表破裂数据，无损数据处理必然导致时间消耗增大，为了在保留地表破裂精细特征的同时降低耗时，可以适当增大计算窗口尺寸或选择并行处理。

4 讨 论

4.1 测量结果的细分

利用本文算法可测量破裂带的整体空间分布、破裂分支的空间分布及破裂空区，但对于规模较小的次级破裂或破裂分布较为弥散的情况，无法自动细分处理，需要人为干预。

4.2 运算性能的优化

在Idaho Lost River地震中，根据破裂带走向分段批处理测量破裂分布形态，同时基于破裂分布密度剔除空白阶区内稀少破裂的误差和粗差干扰，从而可获得分布更集中的破裂迹线。这些手段有效减少了算法单次计算量，提高了大数据量文件的快速处理，但海量地表破裂数据的自动化批处理策略还有待优化。此外，实验发现设置较小的测量窗口因子有利于实现无损或相对更高精度的测量，但耗时过多。实际测量中宜采取“两步法”的操作，即先用较大测量窗口因子粗测并划分破裂密集区域，再用较小测量窗口因子实际测量，可有效兼顾无损测量与效率的平衡。但测量窗口因子的选取严重依赖经验判断，对精度与效率影响较大，测量窗口因子的自适应选取将在后续研究中优化。

玛多地震展示了基于重采样后的破裂数据密度分布跟踪高密度区作为破裂趋势线的形迹，结合密度阈值参数，有助于自动判定规模较大的分支破裂，但密度阈值的确定需要人为干预，因此分支破裂的处理仍需人工二次判读。

4.3 最佳窗口步长的选取

Idaho Lost River地震和玛多地震均显示，随着测量窗口的增大，破裂带宽度的离散程度逐渐减小。因此，对于10 km长的破裂带，测量窗口初始值取50～100 m为宜；对于20 km以上长度的破裂带，测量窗口初始值取100～200 m为宜。原始数据分辨率对测量窗口取值有一定影响，但无直接关系，测量窗口的最佳取值与破裂带变化分布特征关联度更高。

5 结 语

本文基于Python平台，针对高密集度的同震地表破裂数据，设计并实现了一种自动、无损的地表破裂空间形态测量方法和变尺度统计、平滑、制图工具，可实现自动、高效、精细地测量及绘制地表破裂的空间分布形态，提高地震地质调查数据处理与分析效率和精细程度，可为活动断层避让带设定、重点基础设施抗震设防与风险防范提供更加准确的参考。