逆坡倾角对管道水流粗颗粒输送脉动压强影响试验研究

谭伟强，来志强，王仲梅，赵连军，张世宝

（1.华北水利水电大学水利学院，河南 郑州 450045；2.黄河水利委员会黄河水利科学研究院，河南 郑州 450003；3.水利部黄河下游河道与河口治理重点实验室，河南 郑州 450003；4.河南省黄河流域生态环境保护与修复重点实验室，河南 郑州 450003）

0 引 言

近年来，管道输送因价格低廉、操作简单、环境污染较小等优点，在库区清淤排沙、河道疏浚整治、深海石油管道提升、矿石管道长距离输送等领域运用越来越广泛。上述的管道输送工程涉及流体与粗颗粒在管道内共同输送，是典型的管道固液两相流运动问题，往往展示出固体［1，2］和液体［3］的双重特征。

关于管道固液两相流输送机制，国内外学者开展了丰富的研究。曹斌等［4-8］通过一系列清水天然石英砂管道输送物理模型试验研究，研究了管道输送机制和粗颗粒运动机理，研究结果表明管道粗颗粒输送存在滑动推移、跃动推移、滚动推移三种方式。MatouŠek 等［9，10］在进行物理模型试验时，发现在管道输送中粗颗粒会呈现输运层和堆积层的分层现象，颗粒级配会对运动能耗产生影响。夏建新等［11］通过清水管流试验研究了粗颗粒浓度分布规律，构造了颗粒垂线最大浓度点相对位置高度与颗粒粒径、平均流速、管径、重力加速度的函数关系。Vlasák 等［12］以清水为管流载体，通过玄武岩卵石、玻璃球两种材料来模拟不同形状、密度的粗颗粒，试验结果发现两种不同材料粗颗粒的管流水力要素差异不大。但是以上研究主要针对管道流体粗颗粒的输送机制，对管内脉动压强特性研究鲜有涉及。

管道输送时脉动压强特性对管道安全运行具有重要意义。李珊珊等［13］利用小浪底水库现场管道抽沙试验的管道参数，研究其管道阻力随含沙量及流速的变化规律，发现压降均随着含沙量的增大而增大，而当含沙量一定时，压降随流速增长呈指数型增长。Li等［14］研究了高压脉动流体的产生、不同的流体脉动幅值和压力对管件密封特性的影响，结果表明由于流体脉动的作用特性，管件密封特性在脉动周期内呈周期性变化，管件密封接触面积的变化范围与高应力区基本保持一致。李岩等［15］以黄河细沙（d50=107 μm）为研究对象，对有压输沙管道的脉动压强特性进行了物理试验研究，结果表明有压输沙管道脉动压强概率分布符合正态分布。相同流量下，沿程时均压强和峰值压强随含沙浓度增大而增大；相对脉动压强总趋势随含沙量增加而降低。脉动压强波动与湍流能量耗散有密切关系，泥沙与水流相互作用影响着管壁脉动压强的波动。而以上研究主要是对管道清水输送或者含沙水流的脉动压强进行了研究，目前管道流体粗颗粒输送时脉动压强特性变化规律仍处于未知状态。

此外，逆坡管道输送在管道系统布设时经常涉及［16-18］，往往决定了管道整体输送的效率。研究不同管道逆坡倾角条件下流体粗颗粒输送时脉动压强特性变化规律，对于管道安全设计十分重要。因此，本文通过物理模型试验，对倾斜管道流体粗颗粒管道的脉动压强、时均压强、峰值压强、脉动压强概率密度分布以及功率谱等随管道倾角的变化规律开展研究。研究成果将对倾斜管道流体粗颗粒的安全输送设计提供理论基础与技术支撑。

1 试验装置和试验方法

1.1 试验装置

研究团队自行设计了管道流体粗颗粒输送模型试验装置，主要包含3个部分，分别是进口搅拌池与控制系统、有机玻璃管观测测量段、退水系统，示意图见图1。整个循环管道长23 m，管径为0.1 m。进口搅拌池与控制系统包括主输送管道、动力水泵、手动阀门、电磁流量计、粗颗粒投料箱组成；有机玻璃管观测测量段长3 m，沿管壁下部均匀布设压强传感器，测点分别编号为“1～4”，压强传感器间隔为0.5 m，采样频率为50 Hz，采样时间间隔为0.02 s；退水系统包含退水池和粗颗粒过滤装置。

1.2 试验方法

本项目管道水力输送的流体介质为清水。天然卵石形状各异，试验时无法保证每组工况下各卵石形状完全一致。为排除卵石形状影响，本试验采用圆球状35%氧化锆研磨珠作为模拟材料。此模拟材料的密度、恢复系数、刚度等物理力学特性参数与天然卵石的参数值相差不超过3%，且每个颗粒的物理力学参数一致。模拟材料的粒径选为4 mm［模拟材料如图1（b）左上角所示］。试验时管流平均流速为1.5 m∕s，粗颗粒的水沙比0.004 5，为研究管道倾斜角度的影响，管道逆坡倾斜角度分别为10°、20°和30°。

图1 倾斜管道粗颗粒水力输送物理模型试验装置Fig.1 Physical model test device of inclined pipe coarse particle hydraulic transport

首先启动压强传感器采集系统，设置各种参数，等待数据采集。在传感器采集系统设置完成后，启动动力水泵，调节管流流速，当管流流速达到1.5 m∕s 并处于稳定状态后，开始数据采集，从粗颗粒投料口按照试验要求使用投料机将4 mm 粗颗粒均匀投放到管道中，在管流带动作用下，粗颗粒运动至倾斜观测段，粗颗粒投放时间为20 s。采集从粗颗粒投料前至粗颗粒完全离开管道后一段时间管壁的实测压强。

2 实测管壁压强

粗颗粒管道输送与细颗粒管道输送不同，细颗粒在输送过程中，往往与水流会形成新的流体，以悬移输送为主，部分细颗粒会随着输送过程逐渐沉降进行推移输送；粗颗粒水力输送时，颗粒主要以推移为主，极少部分单颗颗粒会悬浮在水中悬浮输送，泥沙和水流会形成明显的分界面。本试验当粗颗粒投料以后，颗粒在倾斜管道中会形成较薄一层粒子团，随倾斜角度增加，粒子团的厚度降低。在输送过程中粒子团占管道的过流面积较少，对过水面无影响。

通过管道脉动压强传感器和DHDAS 压强采集系统采集并记录管壁的瞬时压强随时间的变化值，如图2所示。图2为2号传感器位置在粗颗粒粒径d为4 mm、粗颗粒的水沙比0.004 5、管道流速v为1.5 m∕s、管道倾斜角度θ为10°、20°和30°时的实测瞬时压强分布图。由图2可知，随着管道倾斜角度的增大，瞬时压强整体分布逐渐减小，但波动性增大。图2中t0为粗颗粒开始进入管道时刻，t1为粗颗粒完全离开管道时刻。

图2 不同倾斜角度条件下2号位置实测瞬时压强分布图Fig.2 Measured instantaneous pressure distribution of No.2 pressure sensor under different tilt angles

3 压强脉动特性分析

3.1 时均压强

试验过程中通过压强传感器采集到的实测的瞬时压强p由两部分构成，即时均压强>和脉动压强p′，其表达式为p=+p′。时均压强为实测瞬时压强的平均值；脉动压强为管道的实测瞬时压强减去相应的时均压强，脉动压强反映了管流的波动性。

管道流体粗颗粒输送主要是管道前后的压差提供驱动力，在粗颗粒管道输送过程中，时均压强的变化是固液两相流管道输送的重要参数。图3为倾斜角度为10°、20°和30°条件下沿程时均压强分布图。有机玻璃试验观察段的总长度为L，以第一个压强传感器位置为横坐标的0 基准测点，各测点距第一个压强传感器位置的距离为x。由图3可知，各测点的时均压强值均沿程呈线性降低的趋势，这是由于沿程有能量损耗；随倾斜角度增加，各个压强测点所得的时均压强值均随之减小，这是由于随倾斜角度增加，出口高度增大，沿程能量损耗增加所致。当管道倾斜角度分别为10°、20°和30°时，沿程时均压强拟合函数分别为y=-1.31x+6.07（R2=0.98）、y=-1.96x+5.52（R2=0.99）、y=-2.31x+5.46（R2=0.99），线性拟合相关性显著。管道倾斜角度越大，拟合直线斜率的绝对值增大，表明沿程压强损失加快。

图3 不同倾斜角度条件下沿程时均压强分布Fig.3 Time-average pressures under different tilt angles

3.2 脉动压强

脉动压强的变化是一个随机的过程，是水流质点相互碰撞、混掺作用的结果，在有压管流中，脉动压强会对管道稳定性与安全性产生重要影响。图4为倾斜角度为10°、20°和30°条件下的脉动压强分布图，因时均压强值为常数，脉动压强分布波形图与实测瞬时压强波形图分布一致。由图4可知，随倾斜角度的增加，脉动压强的波动性增加。

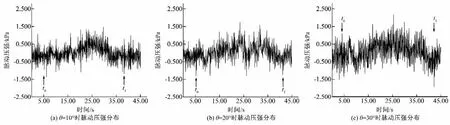
图4 不同倾斜角度条件下2号位置脉动压强分布图Fig.4 Fluctuating pressure distribution of No.2 pressure sensor under different tilt angles

为量化脉动压强波动性，分析不同管道倾斜角度条件下脉动压强分布方差，不同倾斜角度条件下2 号传感器位置的脉动压强（实测瞬时压强）的方差如图5所示，由图5可以看出，随倾斜角度的增大，方差值由0.204 增大至0.351，脉动压强的波动性显著增强，实测瞬时压强的波动性同样显著增强。

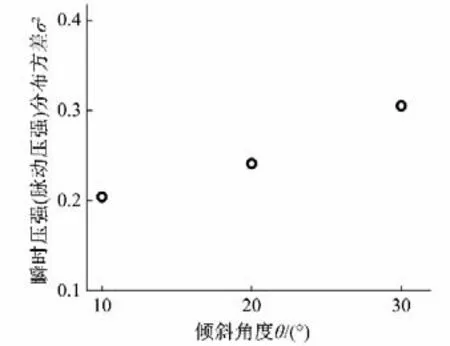
图5 不同倾斜角度条件下2号位置脉动压强（实测瞬时压强）方差值分布图Fig.5 Distribution of variance values of fluctuating pressure（measured instantaneous pressure） at the position of sensor 2 under different tilt angles

3.3 峰值压强

峰值压强是指管道流体粗颗粒运动引起的压强最大值，会在一瞬间对管道的管壁造成强烈的冲击，当峰值过大时，会导致管道发生严重变形甚至爆裂，损坏管道结构。峰值压强包含瞬时峰值压强和脉动峰值压强，对管道的稳定性和安全性具有重要影响。图6给出了不同倾斜角度条件下瞬时峰值压强、脉动峰值压强变化情况。由图6可知，不同倾斜角度对应的瞬时峰值压强、脉动峰值压强变化的规律相反。随管流倾斜角度的增加，瞬时峰值压强呈线性趋势增加。当倾斜角度为10°、20°和30°时，瞬时峰值压强1 至4 号压强传感器拟合函数及相关系数分别为：y=-0.01x+7.96（R2=0.99）、y=-0.04x+6.46（R2=0.95）、y=-0.12x+6.03（R2=0.89）、y=-0.20x+5.29（R2=0.98）。这是由于倾斜角度增加，管道沿程能量耗增加；随倾斜角度增加，脉动压强呈现增加的趋势，1 至4 号压强传感器平均值符合线性分布，其拟合函数表达式为y=0.01x+1.42（R2=0.99）。

3.4 脉动压强的振幅概率分布和振幅正态分布拟合函数图

倾斜管道流体粗颗粒输送管壁脉动压强是一种随机荷载现象，是管道各流层间水流质点相互紊动、碰撞的结果。概率密度函数是脉动压强振幅的一个重要特征［19］。图7为不同倾斜角度条件下2号压强传感器位置处脉动压强振幅概率密度分布规律。由图7可知，随管道倾斜角度的增加，脉动压强的频率分布直方图最大频数的直方图逐渐减小；脉动压强振幅范围逐渐增加；脉动压强振幅频率分布特征均可采用高斯分布函数［20］（Guass分布函数，又称为正态分布函数）描述。拟合函数如下：

图7 不同倾斜角度条件下脉动压强振幅概率分布Fig.7 Probability distribution of fluctuating pressure amplitude under different tilt angles

式中：f(p)为脉动压强的振幅概率密度拟合函数；u为脉动压强的期望；σ为脉动压强方差。u为概率密度拟合函数的位置参数，决定分布函数的位置；σ为概率密度拟合函数的形状参数，决定分布函数的离散程度，σ越大，数据分布越分散，σ越小，数据分布越集中。

由实测瞬时压强=时均压强+脉动压强可得，脉动压强是一种围绕时均压强随机波动过程，其均值为0，故脉动压强的振幅概率分布拟合函数为均值近似为0 的高斯分布。图8为在不同倾斜角度下的脉动压强概率密度曲线，由图8可知，当管道倾斜角度由10°增加到30°时，概率函数分布由“瘦高”型逐渐向“矮胖”型发展。当管道倾斜角度分别为10°、20°和30°时，脉动压强振幅频率拟合函数及相关系数分别为y=2.72+

图8 不同倾斜角度条件下脉动压强振幅概率密度拟合函数图Fig.8 Fitting function diagram of normal distribution of fluctuating pressure amplitude under different tilt angles

粗颗粒脉动压强的最大可能振幅对管道的安全性和稳定性有着重要的意义，振幅过大可能会导致管道爆裂等问题，脉动压强的最大振幅可通过振幅公式=±3σ进行计算，由公式得，当管道倾斜角度分别为10°、20°和30°时，脉动压强的最大振幅分别为，因此脉动压强的振幅随管道倾斜角度的增大逐渐变大，分布形态向远离时均压强变化。

为进一步研究倾斜角度对脉动压强振幅概率概率密度拟合函数的分布规律，可采用峰度系数Ck描述脉动压强振幅的分布形态的陡峭或平缓程度。

峰度为四阶中心距与标准差的四次方的比值，表达式如下：

式中：pi为瞬时压强：为均值压强；σ为脉动压强标准差。

峰度系数Ck越大，说明脉动压强数据中的极端值越多。标准的高斯分布的峰度为0；当峰度小于0 时，称脉动压强分布具有不足的分布，分布函数形态呈现矮胖的现象；当峰度系数大于0 时，脉动压强具有过度的峰度，分布函数形态呈现瘦高的现象。

图9为当管道倾斜角度为10°、20°和30°时脉动压强的峰度系数Ck变化值。由图9可知，脉动压强的峰度系数Ck均大于0，随管道倾斜的增加，峰值系数逐渐趋近于0。这表明倾斜管道的脉动压强分布形态均偏向于瘦高型，随倾斜角度的增加，瘦高现象逐渐减小。总体上倾斜管道的偏度峰度与倾斜角度的相关性较弱，脉动压强振幅分布函数接近标准高斯分布。

图9 不同倾斜角度条件下峰度与管道倾斜角度相关关系Fig.9 Correlation between skewnessand pipeline Inclination under different inclination angles

3.5 脉动压强的频谱特性

水流的脉动现象是由无数大小不一，振幅不同、频率不同、脉动强度和旋转强度不同的涡旋运动引起的，管流底部压强的脉动管流中涡体的不停震荡、分解、组合，不同流层间的质点相互混掺、碰撞，也是这些涡体涡旋运动的反映［21］。对管道流体粗颗粒运动脉动压强的连续波动信号进行快速傅立叶变换（FFT），将脉动压强的时域信号转换为频域信号，可得到脉动压强的振幅谱密度函数、相位谱密度函数和功率谱密度函数［15，22］，即粗颗粒倾斜管道脉动压强的频谱密度函数的分布。

非周期性连续时间信号f(t)的傅立叶变换可以表示为：

倾斜管道流体粗颗粒输送过程中所产生的脉动压强是由具有不同能量的频率分量复杂叠加组合而成，功率均为正值，脉动压强的功率谱曲线与坐标轴围成的面积即为脉动压强的总能量，通过功率谱密度函数曲线分布，可以判定粗颗粒管道内部紊动变化情况。以往含沙管道研究中，湍流的紊动能量主要集中在0～20 Hz 范围内［15，23，24］。将湍流的功率谱分为低频、主频和高频范围，低频范围为0～2 Hz，主频范围为2～20 Hz，高频范围为大于20 Hz，本次研究是管道流体粗颗粒的输送，以往研究成果不能直接应用。

图10为不同倾斜角度条件下脉动压强功率谱分布，由图10可知，随管道倾斜角度的增加，在8～18 Hz主频范围功率谱出现次数显著增大，其功率谱总能量占比也显著增大；各倾斜角度下，脉动压强的优势频率主要在14 Hz左右，随管道倾斜角度增加，优势频率也逐渐增加；不同倾斜角度下的脉动压强的涡旋结构以主频为主，脉动压强的频率分布主要集中在25 Hz以内。

图10 不同倾斜角度条件下脉动压强功率谱Fig.10 Fluctuating pressure power spectrum under different tilt angle conditions

脉动压强的波动与紊流的能量衰减密切相关，倾斜角度的变化，使得管道中压强变化分布不均，水流的紊动结构发生变化。随倾斜角度增加，管道内的小中尺度涡旋相对增加，大尺寸相对减少，主要表现为功率谱函数的频率范围逐渐减小，但优势频率逐渐增加。

4 结 论

通过设计倾斜管道流体粗颗粒输送试验模型，选择管道倾斜角度分别为10°、20°、30°，以粒径为4 mm 的氧化锆颗粒为研究对象，管道流速为1.5 m∕s，粗颗粒的水沙比0.004 5 条件下的分析倾斜管道流体粗颗粒输送的脉动压强，得到以下结论。

（1）随着管道倾斜角度的增大，瞬时压强和脉动压强方差增大，波动性增强，流体内部紊动增强。时均压强随管道倾斜角度增大而整体分布减小，时均压强沿程损失呈线性减小的趋势，拟合直线斜率绝对值随管道倾斜角度增大而减小。瞬时峰值压强随管道倾斜角度增大呈现逐渐减小的趋势，但脉动峰值压强随管道倾斜角度增大而增大。

（2）随管道倾斜角度的增加，脉动压强振幅频率分布特征均可采用高斯分布函数描述，峰度系数与管道倾斜角度的相关性较弱，脉动压强振幅范围变小，函数形态分布满足高斯分布形态，其形态由“瘦高”逐渐向“矮胖”发展。

（3）脉动压强的波动与紊流能量衰减有关，倾斜角度的变化影响管道内部水流的紊乱结果。随倾斜角度的增大，管道内的小中型涡旋增多，大型涡旋减少。功率谱的频率范围减小，但优势频率逐渐向高频率发展。在相同流速情况下，脉动压强能量分量在频率为8～18 Hz 的范围内的数量明显增加，大于25 Hz的能量比较微弱，各倾斜角度下的脉动压强均属于低频和主频脉动。