基于数据融合及残差卷积自编码器的结构损伤识别方法

刘玉驰，蒋玉峰，王树青，马春可

(中国海洋大学 工程学院，山东 青岛 266100)

深海混输立管是深海采矿系统不可或缺的组成部分，其作为海底矿物采集系统及海面采矿船的连接结构，承担着输送矿液混合流体的重要任务[1]。然而，深海混输立管结构作业过程中持续遭受外部风浪流耦合荷载及内部矿液两相流体磨蚀作用，长期作用下结构损伤逐渐积累，恶劣海洋环境作用下极易发生破坏，因此，对深海混输立管结构进行健康监测具有十分重要的意义。深海混输立管结构长达数千米，需要借助于全局损伤检测方法进行结构健康监测，由于方法简单、操作方便及成本低，基于结构振动响应的损伤检测方法得到了研究人员的广泛关注[2]。

传统方法基于结构模态参数进行损伤检测，其基本原理是[3]：从结构动力响应中识别待检测结构模态参数，通过直接与已知健康状态模态参数比较，或构造损伤指标进行结构损伤识别。典型的立管结构损伤识别方法研究详见参考文献[4-6]。然而深海混输立管结构呈高长细比、柔性状态，自然环境荷载激起的模态频率极低，难以通过实测响应识别，同时环境荷载作用下往往存在多阶模态叠加，需要基于大量测点响应确定模态振型，上述模态参数识别中存在的困难进一步限制了该类方法的发展。

为了克服上述不足，研究人员尝试直接基于动力响应进行立管结构损伤检测，从而避免模态参数识别过程中引入的误差。现存的直接基于结构动力响应的损伤识别方法主要包含两大类：基于时间序列模型和基于深度学习模型。就立管结构而言，主要集中在基于时间序列模型方法的研究。Riveros等[7]将自回归(autoregressive，AR)模型与含外生变量的自回归(auto-regressive with extra inputs，ARX)模型相结合进行柔性立管结构损伤识别，研究表明该方法无需有限元模型即可有效识别柔性立管结构损伤。Liu等[8]使用自回归滑动平均(autoregressive moving average，ARMA)模型拟合加速度响应信号，并基于ARMA模型参数变化构造损伤指标进行立管结构损伤识别，通过20 m长立管结构损伤识别数值模拟验证了方法的有效性。然而时间序列模型定阶严重依赖研究人员经验，且模型参数基于最小二乘估计确定，容易使模型陷入局部最优解而非全局最优解。

深度学习模型通过对大量样本数据进行分析处理，基于优化算法自动确定模型参数，摆脱了对研究人员经验的依赖，同时能够更快地寻找到全局最优解，有效克服了时间序列模型存在的不足[9]。一维残差卷积自编码器(one dimension residual convolution autoencoder，1D-RCAE)是深度学习的一种代表性模型，其通过卷积算法自动提取原始输入数据的高级特征，从而基于该特征完成目标任务[10]，由于其数据处理思想与损伤识别思路一致，研究人员提出了多种基于1D-RCAE模型的结构损伤识别方法，详见参考文献[11-14]。目前基于1D-RCAE模型的损伤识别方法多使用单测点响应进行损伤识别，导致提取的特征损伤敏感性有限；部分方法虽然可以基于多测点响应进行损伤识别，但仅仅是将多测点响应简单排列成为三维张量输入1D-RCAE模型，并未实现有效的数据融合，导致输入数据中包含大量冗余信息，严重增加了特征提取复杂性，而且延缓了数据处理的速度。

本文就深海混输立管结构损伤识别问题开展研究，提出了一种基于数据融合及1D-RCAE的结构损伤识别新方法。针对立管结构模态参数识别困难的问题，方法直接以结构损伤敏感的应变动态响应为输入，避免了模态参数识别中存在的误差。针对单测点响应提供损伤信息有限的问题，方法使用主成分分析进行多测点应变响应特征融合，进一步利用1D-RCAE自动提取损伤敏感特征，以结构损伤前后敏感特征间的马氏距离构建结构损伤判定指标，实现混输立管结构健康状态监测。

1 理论方法

1.1 数据融合

深海混输立管结构一般长达数千米，呈高长细比柔性状态，加速度响应损伤敏感性低，而应变响应对结构局部损伤十分敏感，因此本文所提方法基于深海混输立管结构弯曲应变响应进行损伤识别。然而，结构弯曲应变响应仅对局部损伤敏感，因此需要利用多测点响应以提供足够充分的结构损伤信息。但同一结构多测点响应间存在关联，该关联将会在一定程度上掩盖结构损伤引起的动力特性变化，从而增加损伤敏感特征提取复杂性，同时多测点响应中存在大量对样本能量贡献较小的冗余信息，这些信息将会在一定程度上延缓损伤敏感特征提取速度，因此将结构多测点响应简单组合后输入1D-RCAE模型将会增加特征提取的难度及延缓特征提取的速度。

主成分分析(principal component analysis，PCA)可以有效消除多测点响应间相关性，分离并剔除冗余信息[15-16]。因此本文所提方法借助PCA将多测点响应主要信息沿空间方向集中于指定阶主成分上，从而实现多测点响应数据的有效融合，基于PCA的数据融合方法主要流程如下：

(1)取Nm个测点响应组合为响应矩阵X=[x1,x2,…,xNm]，其中测点i响应xi的时刻数为Nt，即响应矩阵X的大小为Nt×Nm。依次对测点i响应xi进行特征值归一化处理，即

(1)

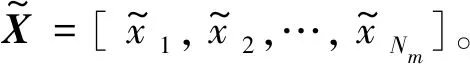
(2)

并对协方差矩阵C进行特征值分析，即

CΦ=ΛΦ

(3)

式中：Λ为特征值矩阵,Λ=diag(λ1,λ2,…,λNm)；Φ为特征向量矩阵，Φ=[φ1,φ2,…,φNm]。

(3)依次计算第Nk阶(Nk=1,2,…,Nm)特征值对应的累积能量占比指标

(4)

(5)

1.2 一维残差卷积自编码器

1D-RCAE的基本组成包括：输入层、卷积层、特征层、解卷积层以及输出层[18]，本文建立的1D-RCAE模型如图1所示，输入层接收输入数据并传递至编码部分，编码部分通过多层卷积层逐步提取输入数据的多类型特征，特征层对编码部分提取到的多类型特征进行整合得到高级特征，解码部分进一步根据高级特征重构输入数据，并通过输出层输出重构结果，1D-RCAE训练过程以最小化响应重构误差为目标，从而保证提取特征的有效性。

图1 1D-RCAE模型Fig.1 Architecture of the 1D-RCAE model

由图1可知，1D-RCAE模型输入数据x为三维张量，张量x包含Nc个通道，每一通道存储长度为1×len的单一向量，即张量大小为1×len×Nc。传统方法将各测点指定时间长度动力响应作为各通道向量，即输入数据通道数目Nc=Nm，其中Nm表示响应测点数；而本文所提方法首先使用PCA方法融合多测点动力响应数据，并将数据融合结果作为1D-RCAE模型的输入，即输入数据通道数目Nc=Nk，其中Nk表示主成分保留阶数。

卷积层通过卷积操作从该层输入数据xconv中提取数据特征，其数据处理方式为

(6)

特征层整合卷积层提取到的多类型特征，输出结果为1×64的向量，所提方法将特征层输出作为损伤敏感特征，并基于此构造损伤指标进行损伤检测。

解卷积层通过转置卷积操作对输入特征xdec进行上采样，从而基于输入特征逐步重构原始输入数据，其数据处理方式为

(7)

1.3 损伤判定

本文所提方法通过计算结构损伤前后敏感特征间的马氏距离构建结构损伤判定指标进行损伤判定，损伤判定流程如下：

(1)依次将阈值确定集(基于已知健康结构响应生成)各样本输入已训练的1D-RCAE模型，提取特征层输出作为基准特征。假定存在Ns个样本，由1.2节1D-RCAE模型架构可知，特征层输出为1×64的向量，因此Ns个样本提取到的基准特征可以组合成为Ns×64的基准特征矩阵F=[f1,f2,…,fNs]T，其中fi表示1D-RCAE模型从阈值确定集样本i中提取到的基准特征，则各基准特征间马氏距离通过式(8)计算

(8)

式中：μf为Ns个基准特征各时刻均值组成的向量，为1×64的向量；Ω为基准特征矩阵F对应的协方差矩阵。使用式(8)根据Ns个基准特征计算得到Ns个马氏距离，并基于3σ准则确定基准阈值，即以Ns个马氏距离的均值加3倍的标准差作为基准阈值。

(2)将待检测结构响应输入已训练的1D-RCAE模型，提取特征层输出作为提取到的特征f′，则f′与上述基准特征间马氏距离通过式(9)计算

(9)

最终通过将D(f′)与上述基准阈值相比较进行损伤判定，即若D(f′)小于基准阈值则判定为健康结构，否则判定结构存在损伤。

1.4 基于数据融合及1D-RCAE的损伤识别方法

本文就深海混输立管结构损伤检测问题开展研究，提出了一种基于数据融合及1D-RCAE的结构损伤识别方法。方法直接基于结构动力响应进行损伤识别，首先使用PCA融合多测点响应信息，然后将融合结果作为1D-RCAE输入，借助于1D-RCAE自动提取损伤敏感特征，最终计算损伤敏感特征与基准特征之间的马氏距离，通过与预设阈值相比较进行损伤判定。

损伤识别方法的流程如图2所示。

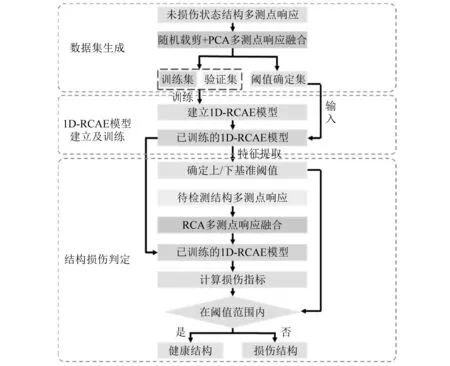
图2 方法实施流程Fig.2 Flowchart of the proposed method

步骤1数据集生成。获取已知未损伤结构Nm个测点响应，使用长度为Nt的时间窗口随机截取Ns组样本，即得到Ns个Nt×Nm的响应矩阵，继而按照1.1节中所述流程借助PCA进行多测点响应融合，假定保留Nk阶主成分，则得到Ns个Nt×Nk的数据融合矩阵，将数据融合矩阵的各阶主成分重组为1×Nt×Nk的三维张量作为最终的样本，将Ns组样本按照指定比例划分为训练/验证/阈值确定数据集。

步骤21D-RCAE模型建立及训练。建立如1.2节所示1D-RCAE模型(Nc=Nk)，使用训练/验证数据集对模型进行训练/预测试，直至响应重构误差满足要求为止，得到已训练的1D-RCAE模型。

步骤3损伤判定阈值确定。将步骤1中阈值确定数据集各样本输入已训练的1D-RCAE模型，使用模型自动提取多样本特征形成基准特征矩阵，基于式(8)计算阈值确定数据集各基准特征间的马氏距离，并基于3σ准则确定损伤判定基准阈值，即以基准特征间马氏距离的均值加3倍标准差作为损伤判定基准阈值。

步骤4待检测结构损伤判定。获取待检测结构Nm个测点响应，按照1.1节中步骤借助PCA融合多测点响应(保留Nk阶主成分)，并将数据融合结果输入已训练的1D-RCAE模型，借助模型自动提取损伤敏感特征，继而基于式(9)计算该特征与步骤3中基准特征之间的马氏距离作为损伤指标，通过与步骤3中基准阈值相比较进行损伤判定，即若小于基准阈值则判定为健康结构，反之判定为损伤结构。

2 数值模拟研究

2.1 有限元模型

利用ANSYS软件建立深海混输立管有限元模型，模型长500 m，顶端与采矿船连接部分简化为固定端约束，底端与软管连接部分简化为自由端。有限元模型划分为57节点56单元，其中：单元1位于水面以上，长度为5 m；单元2～单元56位于水面以下，长度均为9 m。采用PIPE288单元建立有限元模型，单元截面尺寸为Φ 0.18×0.013 m，单元材料属性如下：材料密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3。有限元模型在距离顶部固定端120 m位置(即水面以下115 m位置)设置5 t质量点，用于模拟扬矿泵结构，立管数值模型如图3所示。对深海混输立管有限元模型进行模态分析，模型前6阶固有频率如表1所示，模型前6阶模态振型如图4所示。

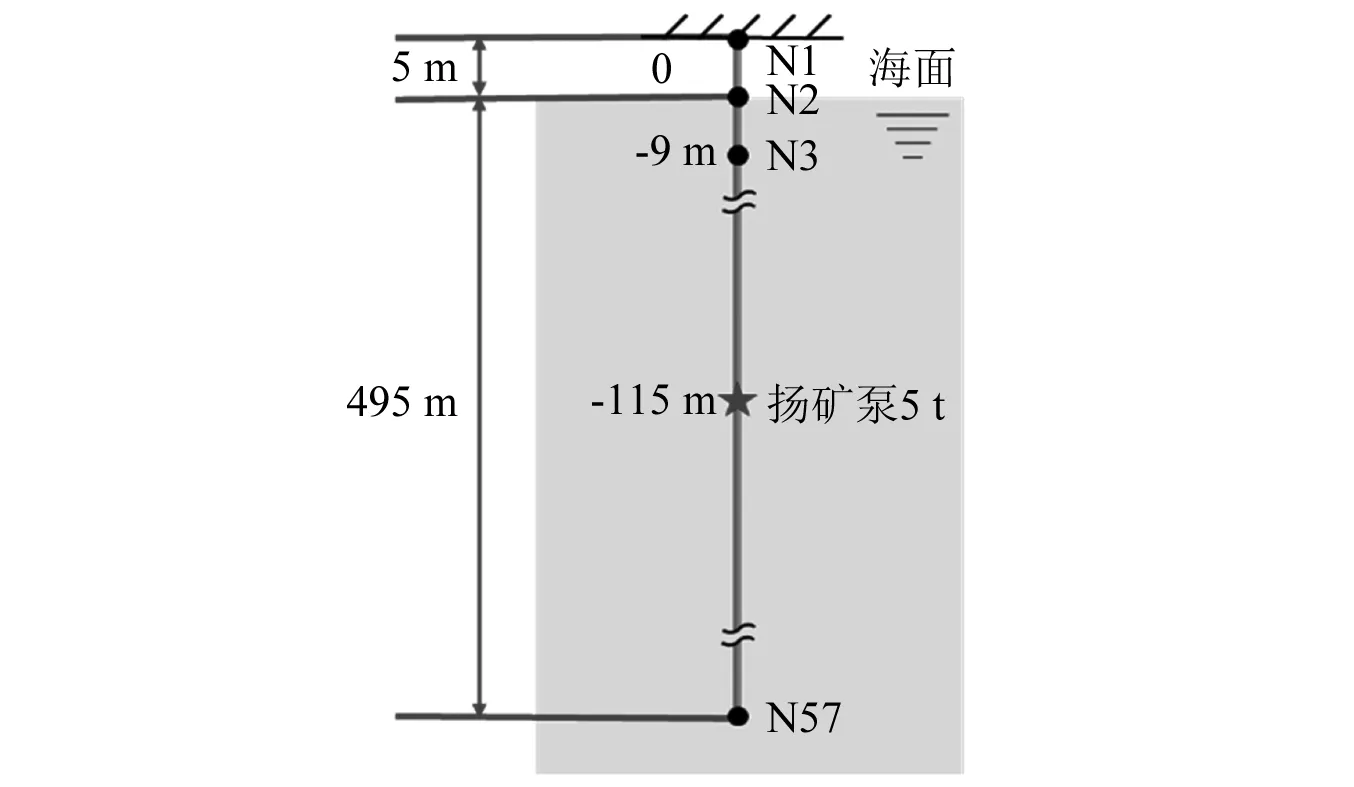
图3 立管数值模型Fig.3 Numerical model of riser

表1 有限元模型前6阶固有频率

深海混输立管作业过程中，海洋环境因素持续变化引起结构动力响应改变，基于结构动力响应的损伤检测方法对该变化敏感，变化海洋环境因素影响下极易发生误判。因此，文章进一步探究变化海洋环境荷载作用条件下方法损伤识别效果，以南海某海域为目标海域，根据目标海域长期观测资料，随机波浪荷载有效波高集中分布于0.8 m附近，有效波周期集中分布于5 s附近，海流荷载相对恒定。因此本文选取目标海域6种典型海况作为拟施加环境荷载，各典型海况随机波及海流参数如表2所示，其中海况1为基准海况，海况1/海况2/海况3及海况1/海况4/海况5/海况6分别用于探究有效波高及有效波周期变化条件下，所提方法损伤识别效果，2.5节将在海洋环境因素变化条件下对方法损伤识别效果进行探究。

图4 有限元模型前6阶模态振型Fig.4 The first six modal shapes of finite element model

表2 随机波及海流荷载参数

2.2 损伤工况及响应提取

深海混输立管结构作业期间，内部固液两相流体流动持续磨蚀内壁面，因此数值模拟中通过单元外径不变、内径扩大的方式模拟壁厚减小损伤。

弯曲应变响应对结构局部损伤敏感，基于弯曲应变响应进行结构状态监测前，需要结合实际情况分析结构易损伤位置，并在易损伤位置附近布置测点，从而实现易损伤位置的重点监测。针对深海混输立管结构的易损伤位置分析如下：①深海混输立管简化为顶端固定、底端自由的悬臂梁结构，顶部固定端应力集中效应明显，易发生损伤；②海面附近结构长期遭受波浪荷载往复作用，极易产生疲劳损伤；③立管结构水面以下115 m位置设置提升泵，提升泵作业期间持续振动带动附近结构振动，长期作用下容易引发疲劳损伤。

根据上述分析，数值模拟中损伤单元及响应测点选取如下：①根据上述易损伤位置分析，设定单元1/单元2/单元14损伤结构状态，并选取单元1/单元2共同相邻节点(节点2)，以及单元14相邻节点(节点14)作为响应测点，用于重点监测易损伤位置状态；②设定单元9损伤状态，探究损伤单元附近无测点情况下的损伤检测效果；设定多种双损伤状态，探究多个单元同时损伤情况下的损伤检测效果；③在节点2与节点14之间均匀布置3个测点，分别为节点5/节点8/节点11，用于监测深海混输立管结构0～120 m内结构状态。最终选取节点2/节点5/节点8/节点11/节点14为响应测点，损伤工况设定如表3所示，损伤单元及响应测点位置如图5所示。

表3 损伤工况

图5 响应测点及损伤单元位置(m)Fig.5 Position of measuring point and damage element (m)

2.3 无噪声单海况条件下损伤识别

以表2中海况1作用为例，探究单海况条件下方法损伤识别性能。数值模拟流程如下：

步骤1动力响应获取。在ANSYS软件中对表3中8种结构状态对应的有限元模型施加海况1波流耦合荷载并进行瞬态分析，提取节点2/节点5/节点8/节点11/节点14弯曲应变响应，响应提取时长为3 000 s，采样频率为10 Hz。

步骤2数据集生成。使用长度为1 024的时间窗口对健康状态下各测点0～1 000 s响应进行随机裁剪，生成2 200组样本，各样本为 1 024×5的响应矩阵，并将响应矩阵转化为1×1 024×5的张量。将上述样本按照5 ∶1 ∶5的比例划分为训练/验证/阈值确定集，样本数目分别为1 000/200/1 000。使用长度为1 024的时间窗口分别对健康状态下各测点1 000～2 000 s响应与表3中7种损伤状态下各测点1 000～2 000 s响应进行随机裁剪，生成各结构状态对应的测试数据集，对应于8种结构状态存在8个测试数据集，各测试数据集样本数目均为1 000，各样本均为1×1 024×5的张量。

步骤31D-RCAE模型训练及阈值确定。按照1.2节中架构建立1D-RCAE模型后，使用训练/验证数据集完成1D-RCAE模型训练，将阈值确定集各样本输入已训练的1D-RCAE模型提取数据特征，并基于特征间马氏距离确定损伤判定基准阈值。

步骤4结构损伤识别。将测试集各样本输入已训练的1D-RCAE模型提取数据特征，计算该特征与基准特征之间的马氏距离，并通过与上述损伤判定基准阈值相比较进行损伤判定，若提取特征小于损伤判定基准阈值则判定为健康结构，反之判定为损伤结构。

2.3.1 单测点响应损伤识别分析

首先探究仅基于单测点弯曲应变响应的损伤识别效果，即分别以上述各样本中节点2/节点5/节点8/节点11/节点14的单一弯曲应变响应(即样本各通道数据)作为1D-RCAE模型输入进行损伤判定，通过计算测试集中准确识别结构状态的样本数目与总样本数目比值确定损伤识别准确率，损伤判定结果，如表4所示。

表4 单测点响应损伤识别结果

由表4可知，仅使用单测点弯曲应变响应进行损伤识别：①当结构未发生损伤时，利用任一测点响应对健康结构状态(工况A)损伤识别准确率均高于99%，即极少发生将健康结构误判为损伤结构的现象；②基于节点2弯曲应变响应可以准确识别单元1/单元2损伤结构状态(工况B/工况C/工况F/工况G)，而无法识别单元9/单元12/单元14损伤的结构状态(工况D/工况E/工况H)，即当结构存在损伤时，损伤附近测点弯曲应变响应对成功识别损伤至关重要，节点8/节点14弯曲应变响应损伤识别结果同样证明了该结论；③双损伤工况(工况F/工况G/工况H)识别准确率较单损伤工况(工况B/工况C/工况D/工况E)有所提升，即随着损伤单元数目的增加，损伤判定准确率随之增加。

2.3.2 多测点响应损伤识别分析

由2.3.1节损伤识别结果可知，单测点弯曲应变响应仅对测点附近的损伤敏感，仅使用单测点弯曲应变响应难以监测深海混输立管结构整体健康状态，需要使用多测点弯曲应变响应以扩大损伤识别范围，因此进一步探究基于多测点响应的损伤识别效果。使用PCA方法融合上述各样本中节点2/节点5/节点8/节点11/节点14弯曲应变响应，数据融合过程中计算得到一阶主成分对应的累积能量占比为0.956，大于1.1节中预设阈值ε=0.95，因此主成分阶数Nk设定为1，即数据融合后各样本大小为1×1 024×1，并将融合结果矩阵作为1D-RCAE模型输入进行损伤判定。同时基于传统方法进行损伤识别数值模拟，即直接将2.3.1节中各样本(大小为1×1 024×5的张量)作为1D-RCAE模型输入进行损伤判定，并将损伤判定结果与所提方法进行比较。需要注意的是，由于所提方法中1D-RCAE模型输入大小为1×1 024×1，传统方法中1D-RCAE模型输入大小为1×1 024×5，即所提方法与传统方法输入数据大小不同，因此需要分别搭建1D-RCAE模型，基于训练/验证数据集进行训练，并基于阈值确定数据集确定基准特征及损伤判定基准阈值。两种方法损伤判定结果如图6所示，图中标注了使用两种方法进行损伤判定时的损伤判定基准阈值，当损伤指标小于损伤判定基准阈值时判定为健康结构，否则判定为损伤结构，同时标注了不同工况下的结构损伤识别准确率，由于损伤指标量级较大，为了方便观察，对损伤指标取以e为底的对数，即以对数马氏距离为纵轴进行绘制。

图6 多测点响应损伤判定结果Fig.6 Damage detection result using multiple response

图6中损伤判定基准阈值确定过程如下：依次将阈值确定数据集各样本输入已训练的1D-RCAE模型进行处理，提取特征层输出作为样本的基准特征，并基于式(8)计算各基准特征对应的马氏距离指标，统计1 000组样本对应的马氏距离指标的均值及标准差，以均值加3倍的标准差作为损伤判定基准阈值，当1D-RCAE模型输入为PCA数据融合结果/数据组合结果时，损伤判定基准阈值分别为134.3/121.5，取以e为底的对数后分别为4.9/4.8。由图6可知：①PCA数据融合及传统数据组合方法对健康结构状态(工况A)损伤识别准确率均高于99%，即能够准确识别健康结构状态；②由于传统数据组合方法输入数据存在大量关联及冗余，难以有效提取到损伤敏感特征，因此无法有效识别单元1及单元9损伤结构状态(工况B/工况D)；而将PCA融合结果作为1D-RCAE模型输入进行损伤判定，由于消除了多测点响应间关联性及剔除了大量冗余信息，能够更加有效地提取到损伤敏感特征，因此可以准确判定多种结构损伤状态(工况B～工况H)；③由于单元1/单元2附近存在响应测点(测点1)，而单元9与响应测点存在一定距离，因此相同损伤程度下(单元壁厚减小10%)，单元9损伤状态(工况D)较单元1/单元2损伤状态(工况B/工况C)的损伤指标显著性低，但依旧可以准确识别出结构损伤；④结构损伤单元数目增加时，损伤识别难度降低，因此对多种双损伤工况(工况F/工况G/工况H)，所提方法与传统方法均可有效识别结构状态。

2.4 含噪声单海况条件下损伤识别

现场实测结构动力响应的过程中，受测量环境及传感器自身稳定性的影响，实测响应信号中存在噪声污染，将会在一定程度上掩盖结构损伤信息，对损伤检测方法效果产生影响。本节进一步探究不同程度噪声污染情况下方法损伤检测稳定性，主要思路如下：引入2.3.1节中提取的海况1作用下节点2/节点5/节点8/节点11/节点14弯曲应变响应，通过向信号中添加高斯白噪声模拟噪声污染信号，并基于噪声污染信号进行损伤检测数值模拟，其中噪声污染程度通过信噪比指标衡量，共模拟了20 db/10 db两种不同程度噪声污染情况。表3中8种工况各存在1 000组测试样本，通过计算1 000组样本中准确识别结构状态的样本数目与总样本数目的比值确定损伤识别准确率，损伤判定结果如图7所示，分别使用三角形、正方形、圆形表示3种不同程度噪声污染情况下的损伤识别准确率，各列分别表示表3中8种结构状态的损伤识别结果。

图7 噪声污染情况下损伤判定结果Fig.7 Damage detection result under noise pollution

由图7可知：①噪声污染对健康结构状态(工况A)识别效果存在轻微影响，但识别准确率始终保持在98%以上；②工况D表示单元9损伤结构状态，由于单元9附近无响应测点，测点响应能够提供的损伤信息有限，因此噪声污染严重(10 db噪声污染)情况下存在一定程度误判，但识别准确率依旧保持在90%以上；③对损伤单元附近存在测点(工况B/工况C/工况E/工况F/工况G)或多个单元损伤(工况F/工况G/工况H)而言，由于测点响应能够提供足够充分的损伤信息，因此多种程度噪声污染情况下均可准确识别结构状态。

2.5 含噪声变化环境因素条件下损伤识别

深海混输立管结构作业期间，海洋环境因素持续变化将会引起结构动力响应改变，而基于结构动力响应的损伤识别方法对该变化敏感，因此变化海洋环境荷载作用下极易发生误判。本节进一步探究变化环境荷载作用条件下方法适用性，同时考虑存在20 db噪声污染情况，主要思路如下：首先引入2.4节中基于海况1作用下健康结构状态响应训练的1D-RCAE模型，同时引入对应的基准特征及损伤判定基准阈值；然后基于海况2～海况7作用下各结构状态响应生成测试数据集，将测试数据集各样本输入已训练的1D-RCAE模型提取数据特征，并计算提取特征与基准特征之间的马氏距离作为损伤判定指标；最后通过比较损伤判定指标与损伤判定基准阈值进行损伤判定，若小于基准阈值则判定为健康结构，反之判定为损伤结构。表3中8种工况各存在1 000组测试样本，通过计算1 000组样本中准确识别结构状态的样本数目与总样本数目比值确定损伤识别准确率，损伤识别结果如图8所示，分别使用6种不同形状的点表示6种不同海况作用条件下损伤识别准确率，各列分别表示表3中8种结构状态的损伤识别结果。

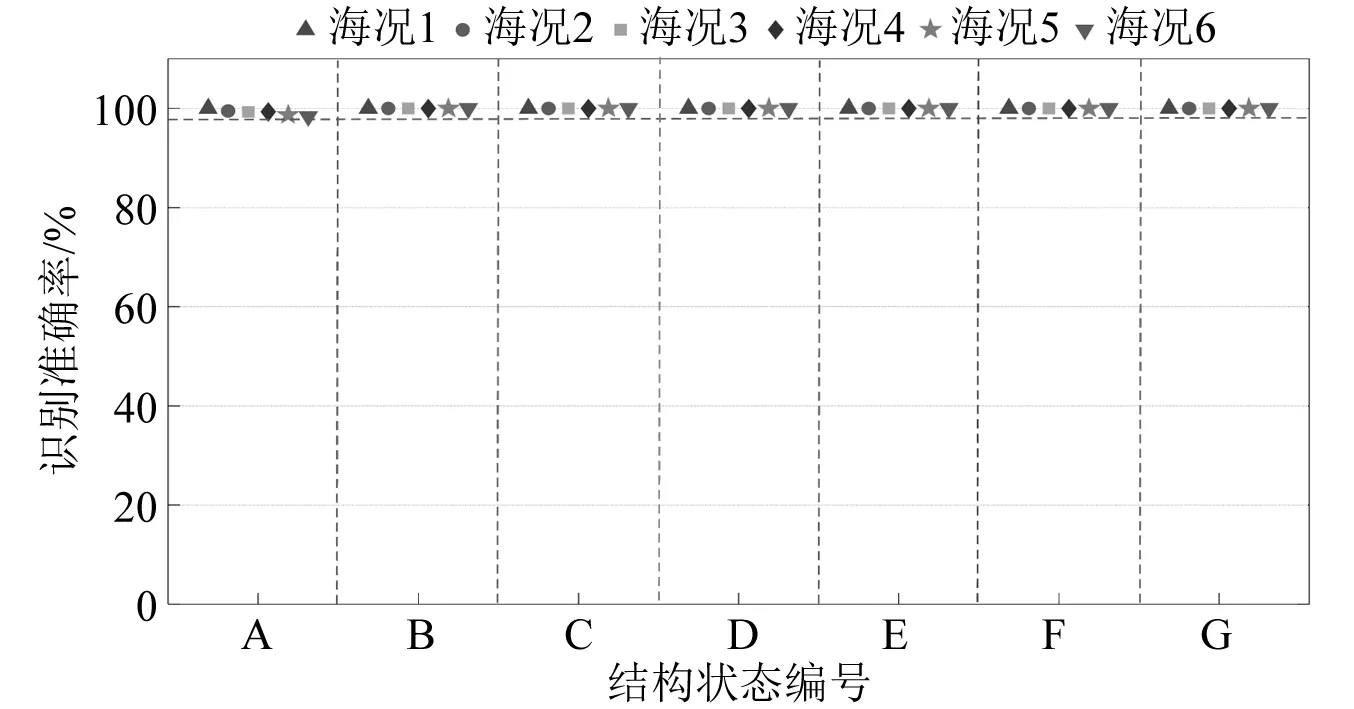
图8 变化环境因素下损伤判定结果Fig.8 Damage detection result under varying environment

由图8可知，考虑20 db噪声污染以及变化海洋环境荷载作用条件下：①健康结构状态(工况A)存在轻微损伤误判现象，有效波高变化(海况1/海况2/海况3)对损伤识别准确率的影响小于有效波周期变化(海况1/海况4/海况5/海况6)情况，且随着有效波周期变化剧烈程度的增加，损伤识别准确率逐渐下降，但变化海洋环境荷载作用条件下识别准确率始终保持在98%以上；②有效波高及有效波周期变化条件下，所提方法均可有效识别多种损伤结构状态(工况B～工况H)。

3 物理模型试验验证

3.1 试验简介

为了进一步验证方法实用性及有效性，在大连理工大学船模拖曳试验水池开展物理模型试验，试验装置主要包括以下三部分：①立管支撑装置。如图9(a)所示，整体尺寸为1 m×1 m×2 m(长×宽×高)，使用高强度卡箍与G型夹固定于桁车上，用于支撑立管物理模型；②立管物理模型，如图9所示，采用玻纤增强聚丙烯管(FRPP管)制成，有效长度为6 m，由12节子管件连接而成，单节子管件长度为0.5 m，管件截面尺寸为Φ 0.02×0.002 5 m，各子管件间通过法兰盘与高强螺栓连接。立管物理模型顶端采用G型夹固定于支撑装置上，底端自由，以实现顶端固定、底端自由的边界条件；③应变数据采集系统，沿深海混输立管物理模型长度方向均匀布置3个测点，测点1/测点2/测点3分别位于单元2/单元5/单元10中点位置(其中测点2用于重点监测水面附近结构状态)，各响应测点位置如图9(b)所示，使用电阻式应变片基于半桥连接方式测量上述测点处模型弯曲应变。对立管物理模型施加波流耦合荷载，其中：①随机波荷载通过造波机施加，有效波高为0.8 m，有效波周期为5 s；②海流荷载施加通过拖车带动立管模型前进实现，海流流速为0.1 m/s。

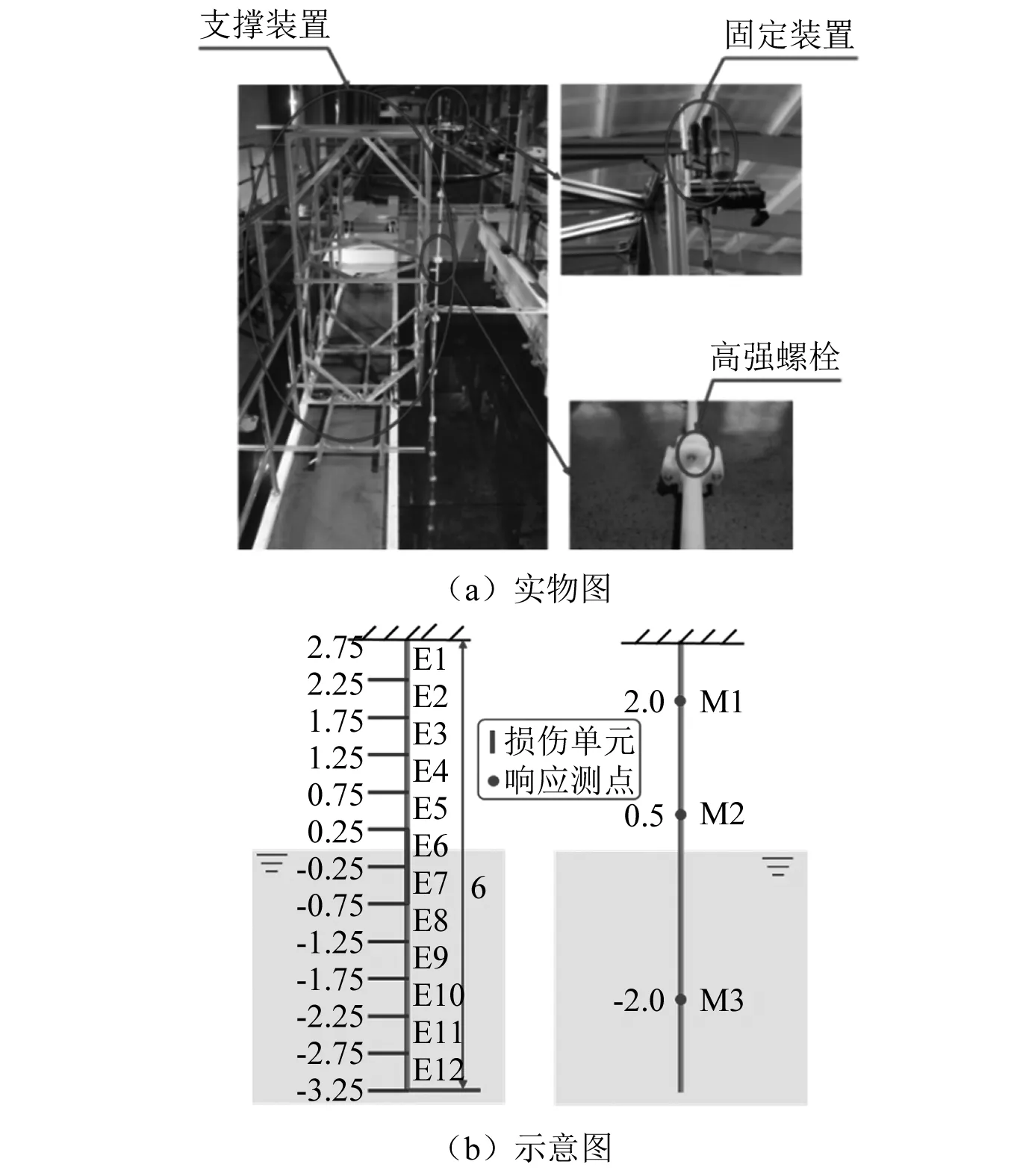
图9 立管物理模型Fig.9 Riser physical model

3.2 损伤工况及响应采集

基于与2.2节中相同原因，通过外径不变、扩大内径的方式模拟壁厚减小损伤，并将指定位置健康子管件替换为损伤子管件引入结构损伤。基于2.2节中易损伤位置分析，水面附近部分结构易发生损伤，因此设定水面附近单元(单元6/单元7)损伤工况，同时考虑多种损伤程度。损伤单元位置见图9(b)，最终设定损伤工况如表5所示。

表5 损伤工况

对立管物理模型施加3.1节中指定环境荷载，通过传感器采集系统获取结构指定测点弯曲应变响应。应变响应采集时长为1 800 s，采样频率为50 Hz。

3.3 损伤识别结果

引入3.2节中提取的健康状态结构测点1/测点2/测点3弯曲应变响应，使用长度为对1 024的时间窗口对健康状态1～600 s响应进行随机裁剪获取1 100组样本，即形成1 100组1 024×3的弯曲应变响应矩阵，将上述样本按照5 ∶1 ∶5的比例划分为训练/验证/阈值确定集，样本数目分别为500/100/500。然后使用长度为对1 024的时间窗口对健康状态及4种损伤状态600～1 800 s响应进行随机裁剪，为各结构状态均生成1 000组样本，各样本大小均为1 024×3。使用PCA融合上述各样本中测点1/测点2/测点3弯曲应变响应，通过计算可知，一阶主成分对应累积能量占比为0.963，大于1.1节中预设阈值ε=0.95，因此主成分保留阶数Nk设定为1，并将数据融合结果重组为大小为1×1 024×1的三维张量。使用训练/验证集完成1D-RCAE模型训练后，将阈值确定集各样本输入已训练的1D-RCAE模型提取数据特征，并基于特征间马氏距离确定基准阈值，继而将测试数据集各样本输入已训练的1D-RCAE模型提取数据特征，计算该特征与基准特征之间的马氏距离，并通过与上述阈值相比较进行损伤判定。损伤判定结果如图10所示，图中标注了使用所提方法进行损伤判定时的损伤判定基准阈值，当损伤指标小于损伤判定基准阈值时判定为健康结构，否则判定为损伤结构，同时标注了不同工况下的结构损伤识别准确率。由于损伤指标量级较大，为了方便观察，对损伤指标取以e为底的对数，即以对数马氏距离为纵轴进行绘制。

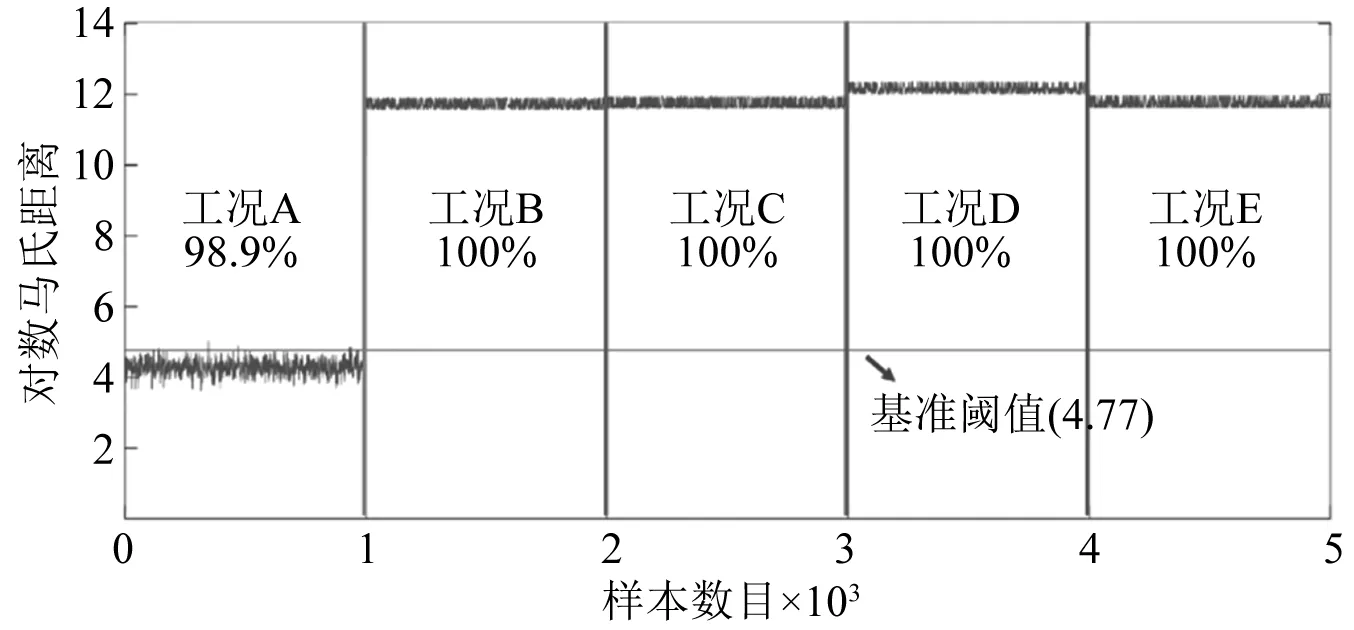
图10 PCA数据融合损伤判定结果Fig.10 Damage detection result using PCA data fusion

图10中损伤判定基准阈值确定过程如下：依次将阈值确定数据集各样本输入已训练的1D-RCAE模型进行处理，提取特征层输出作为样本的基准特征，并基于式(8)计算各基准特征对应的马氏距离指标，统计500组样本对应的马氏距离指标的均值及标准差，以均值加3倍的标准差作为损伤判定基准阈值，最终确定损伤判定基准阈值为118，取以e为底的对数后为4.77。由图10可知：①健康结构损伤识别准确率为98.9%，即极少发生将健康结构误判为损伤结构的现象；②损伤结构状态识别准确率均为100%，即所提方法可以准确识别多种损伤结构状态；③对比单元6不同损伤程度结构状态(工况B/工况C/工况D)的损伤指标可知，单元损伤程度越大，损伤指标显著性更高。

3.4 损伤定位结果

在完成结构损伤判定的基础上，进一步实现结构损伤定位，损伤定位思路如下：由于测点与损伤位置间距离越小，损伤引起该测点结构动力特性变化越明显，因此判定结构存在损伤后，首先基于健康状态结构动力响应训练1D-RCAE模型，并使用已训练的1D-RCAE模型分别处理健康状态结构各测点响应，确定各测点对应的基准特征；然后使用已训练的1D-RCAE模型分别提取损伤结构各测点响应特征，并计算各测点响应提取特征与对应测点基准特征间马氏距离，作为对应测点的损伤定位指标；最终通过比较各测点损伤定位指标进行损伤定位，即判定损伤定位指标显著大的测点附近存在结构损伤。

为了验证方法损伤定位效果，对表5中工况B/工况E进行损伤定位模拟，损伤定位结果如图11所示。

由图11可知，测点2对应损伤定位指标最大，其次为测点3，因此可以判定损伤单元位于测点2与测点3之间，且与测点2间距离最小，损伤定位结果与实际损伤单元位置(见图9)相符合，即所提方法能够有效识别结构损伤位置。

图11 损伤定位结果Fig.11 Results of damage location prediction

4 结 论

本文就深海混输立管结构损伤识别开展研究，针对损伤识别过程中存在的模态参数识别困难、海洋环境因素变化引起损伤误判等问题，提出了一种基于数据融合及1D-RCAE的结构损伤识别方法，方法首先借助PCA沿空间方向将多测点响应信息集中到指定阶主成分上，从而实现多测点响应融合，然后将融合结果作为1D-RCAE输入，使用1D-RCAE自动提取损伤敏感特征，并以损伤敏感特征与基准特征之间的马氏距离作为损伤指标进行结构损伤识别。数值模拟及物理模型试验研究结果均表明，本文提出的方法能够有效实现深海混输立管结构损伤识别，可为深海采矿系统的正常运行提供保障。具体结论如下：

(1)测点距离损伤单元较远时，弯曲应变响应损伤敏感性较低，因此基于弯曲应变响应监测结构状态前，需要结合实际情况分析结构易损伤位置，从而优化传感器布置。

(2)当监测目标为深海混输立管整体结构时，仅使用单测点弯曲应变响应损伤敏感性不足，需要综合利用多测点弯曲应变响应信息以扩大损伤识别范围。

(3)相较于传统数据组合方式，使用PCA融合多测点响应可以消除多测点响应间关联性，同时剔除冗余信息，有助于1D-RCAE模型提取到更加有效的损伤敏感特征，从而提高损伤识别准确率。

(4)噪声污染及变化海洋环境荷载作用条件下，所提方法能够在仅使用有限测点弯曲应变响应的情况下有效识别深海混输立管结构损伤，即所提方法具有良好的噪声鲁棒性，同时对海洋环境荷载变化具有良好的适应性。