汽车电子节气门RBF神经网络控制方法

陈和娟，涂宏庆

（1.无锡商业职业技术学院，江苏 无锡 214153；2.南京工程学院，江苏 南京 2 111167）

1 引言

节气门是汽车发动机的重要部件之一，被称为发动机的“咽喉”，其主要功能是通过传感器信号控制阀片开度，从而调整发动机进气量，进而控制气缸内燃料的燃烧。合理的节气门控制系统和控制方法对提高发动机性能以及减少有害气体排放具有十分重要的作用，是汽车领域的关键技术之一，受到广泛关注［1-3］。

传统机械节气门由油门踏板与阀片机械连接，通过驾驶员操作直接控制，由于其人为主观因素大、可控性不强以及稳定性差等缺点，逐步被电子节气门系统替代，汽车电子节气门控制方法也随之成为汽车、电子以及控制等领域专家学者的研究重点之一。文献［4-6］基于电子节气门构造及工作特性建立了动态数学模型，为其控制方法研究奠定了基础，但上述文献建模过程均进行了问题简化，没有充分考虑摩擦、弹簧等带来的非线性特性；文献［7-9］在上述文献基础上，建立了更为精确的数学模型，并提出了基于自适应控制的电子节气门控制方法，但仍存在未考虑空气阻力影响的缺陷；文献［10］基于此对电子节气门数学模型进行了进一步优化，并充分考虑各种非线性以及外界干扰等不确定性因素，提出一种滑模控制方法，实现了阀门角度的精确跟踪控制；文献［11］在精确建模的基础上，从性能优化的角度，提出了一种模型预测控制方法，进一步提高了系统抗干扰能力；文献［12］针对电子节气门的不确定特性，对传统PID控制方法进行改进，提出一种PI 鲁棒控制方法，降低了超调量，提高了系统的稳定性。但文献［10-12］均需获得精确的节气门模型参数，未考虑模型参数误差带来的建模不精确性。

这里针对上述问题，提出了一种RBF神经网络控制方法，解决传动控制方法需要精确建模的问题。首先，对电子节气门的工作特性进行分析，并充分考虑参数不精确和外界干扰等不确定性，建立其数学模型的状态空间表达形式。而后，基于传统滑模控制理论，提出了抗外部干扰的滑模控制方法。进而，利用RBF 神经网络对控制器不确定部分进行在线逼近，提出一种局部逼近的神经网络控制方法，并通过Lyapunov方法证明了控制系统的稳定性。最后，基于Matlab/Simulink 平台进行对比仿真实验。实验结果表明，所提控制方法能够有效克服外部干扰以及模型参数带来的不确定性，实现电子节气门实际开度对目标开度的精确跟踪。

2 电子节气门工作原理及建模

2.1 电子节气门工作原理

电子节气门基本结构，如图1所示。其工作原理，如图2所示。基本流程为：驾驶员踩下加速踏板形成期望阀门开度信号，与节气门传感器收到的实际阀门开度信号共同作为控制单元的输入信号，控制单元根据给定控制方法计算输出扭矩信号，并传输给PWM模块，经调制后传输给直流电机产生扭矩，控制节气门阀片开度实现对目标阀门开度的实时跟踪。

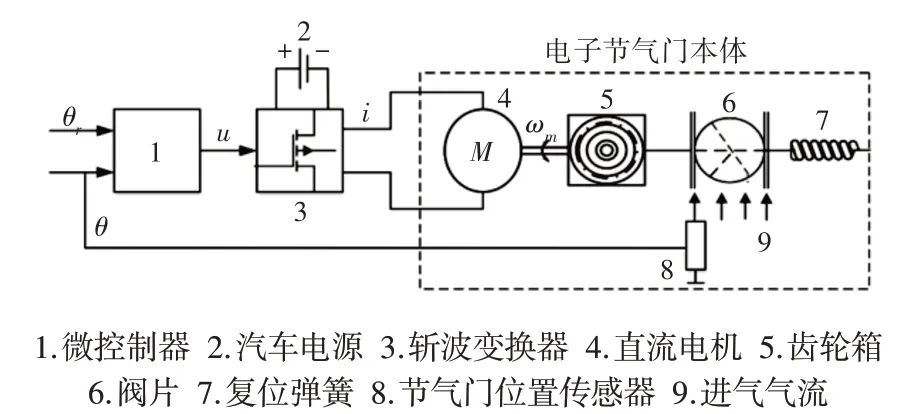
图1 电子节气门结构图Fig.1 Structure Diagram of Electronic Throttle

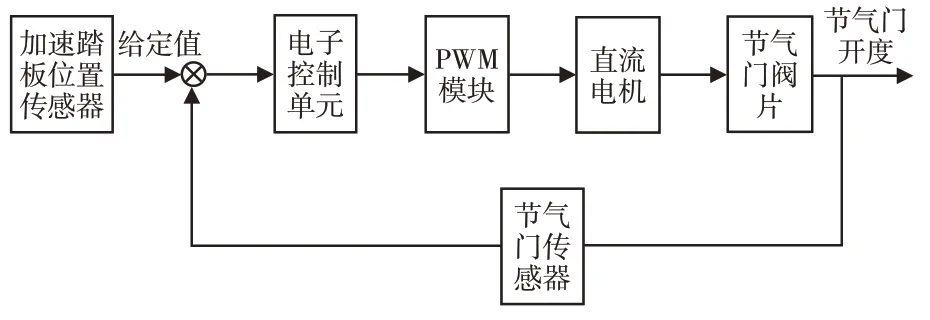
图2 电子节气门工作原理图Fig.2 Schematic Diagram of Electronic Throttle

综上可以看出，电子控制单元是电子节气门的“大脑”，其输入量为阀门期望开度和传感器探测的实时开度，输出为扭矩控制电压信号，控制目标为设计合理、稳定的控制方法以实现目标阀门开度对期望阀门开度的精确跟踪。

2.2 电子节气门数学建模

建立合理、可靠的电子节气门数学模型，是设计其控制方法的前提，大量文献对电子节气门模型建立进行了研究。其中，文献［10］综合考虑电子节气门摩擦、复位弹簧等非线性特性以及空气阻力动态特性，建立了更为精确的数学模型，这里基于此模型，进一步考虑模型参数中的不确定性，建立不确定性电子节气门数学模型。首先，定义状态变量x=[x1x2]，且有：

结合电子节气门运行原理，可得其状态方程为［10］：

令，

则式（2）可写成：

式中：θ—传感器测得的节气门实时角度；JR—系统转动惯量；Ra—电枢回路电阻；Ka—反电动势系数；Kt—力矩常数；Kd—滑动摩擦系数；Ks—弹性系数；Kk表示库伦摩擦系数；Km—力矩补偿系数；j—减速比；u(t)—电机的输入电压；d(t)—外部干扰，其满足：

式中：D—外部干扰上限，为正常数。

进一步考虑模型参数不精确性，则状态方程式（4）更新为：

其中，

其 中，μ0=+Δμ0，μ1=+Δμ1，μ2=+Δμ2，μ3=+Δμ3，μ4=+Δμ4，其中Δμ0、Δμ1、Δμ2、Δμ3、Δμ4分别表示参数不精确带来的误差项。

3 电子节气门的RBF神经网络控制

3.1 RBF神经网络

相关研究表明，RBF神经网络对非线性函数在一定条件下具有逼近特性［13］，且由于其具备较强的泛化能力、结构简单、计算速度快等优点，在非线性系统中得到了很好的运用。如图3所示，RBF神经网络由三层结构组成，分别为输入、隐含和输出层，其中隐含层输出以及网络的输出形式如下［14］：

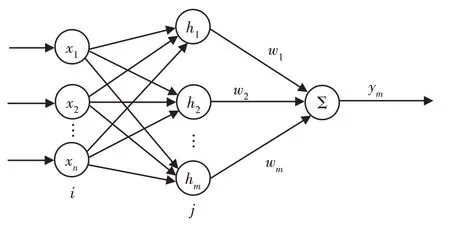
图3 RBF网络结构Fig.3 Network Structure of RBF

式中：φi—第i条神经元的隐含层输出；

ci—第i条神经元的中心矢量；

x—系统输入；

σi—第i条神经元的隐含层的高斯基函数宽度；

f(x)—神经网络输出；

W*—网络理想权值；

ς—逼近误差，且满足 |ς|≤ςN。

3.2 控制器设计

根据跟踪控制目标，定义误差函数为：

式中：θ、θd—传感器测得的节气门阀门实时开度以及期望开度。

当不考虑模型参数的不精确性，即函数和均精确已知时，将式（4）和式（10）代入式（11）中，可得：

则根据滑模控制理论，可设计控制律为：

将控制律式（13）代入到方程式（12）中，可得：

选取参数η使得其满足D≤η，则有：

上式证明当模型参数精确时，控制律式（13）能够使得系统满足渐进稳定性。

实际工程中，电子节气门的模型参数往往存在一定范围误差，为此采用RBF 神经网络对状态方程式（6）中的函数g(x)和f(x)进行在线逼近，定义输入为x=[x1x2]，则神经网络的理想输出和实际输出分别为：

根据式（16）、式（17），得出神经网络输出误差为：

式中：φg(x)和φf(x)—神经网络的高斯基函数；W、W*和V、V*—网络在线估计参数和理想权值参数；ςf、ςg—逼近误差，且满足|ςf|≤ςN、|ςg|≤ςM。

将神经网络的实际输出代入滑模控制律式（13）中，可获得神经网络控制律表达式为：

将式（19）代入式（12）中，可得：

由此，设计参数的自适应调节律为：

3.3 稳定性分析

定义控制系统的Lyapunov函数为：

对Lyapunov函数求导，则有：

将自适应调节律式（21）代入上式，则有：

由于参数d(t)、ςf和ςg均有界，且满足|d(t) |≤D、|ςf|≤ςN、|ςg|≤ςM。则可取η≥η0+ςN+ςMu+D，其中η0≥0，使得：

综上，由于L≥0且≤0，系统满足李雅普诺夫稳定性判据，即有

4 仿真实验

基于Matlab/Simulink平台进行仿真实验，其中将电子节气门初始阀门开度设置为θ0(t)=20rad，外部高频噪声设置为d(t)=5 sin(0.2t)，电动机铭牌参数以及节气门相关参数参考文献［10］中所提供的数据，如表1所示。

表1 电子节气门参考模型参数Tab.1 Reference Model Parameters of Electronic Throttle

实际工程中，上述给出的参数往往存在一定程度误差，设定电子节气门实际参数，如表2所示。

表2 电子节气门实际模型参数Tab.2 Actual Model Parameters of Electronic Throttle

考虑上述外部噪声以及模型误差，分别使用这里所提控制方法以及传统滑模控制方法进行对比实验，以验证所提控制方法的有效性，实验目标为对电子节气门阀门开度的（10～60)°的阶跃信号进行跟踪，仿真时长1000ms，Simulink仿真框图，如图4所示。仿真实验结果，如图5～图9所示。

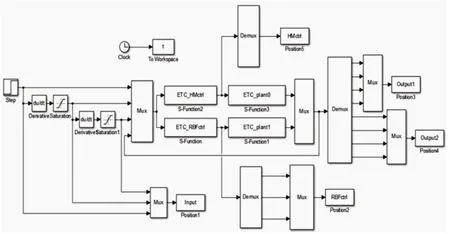
图4 Simulink仿真框图Fig.4 Simulink Simulation Block Diagram

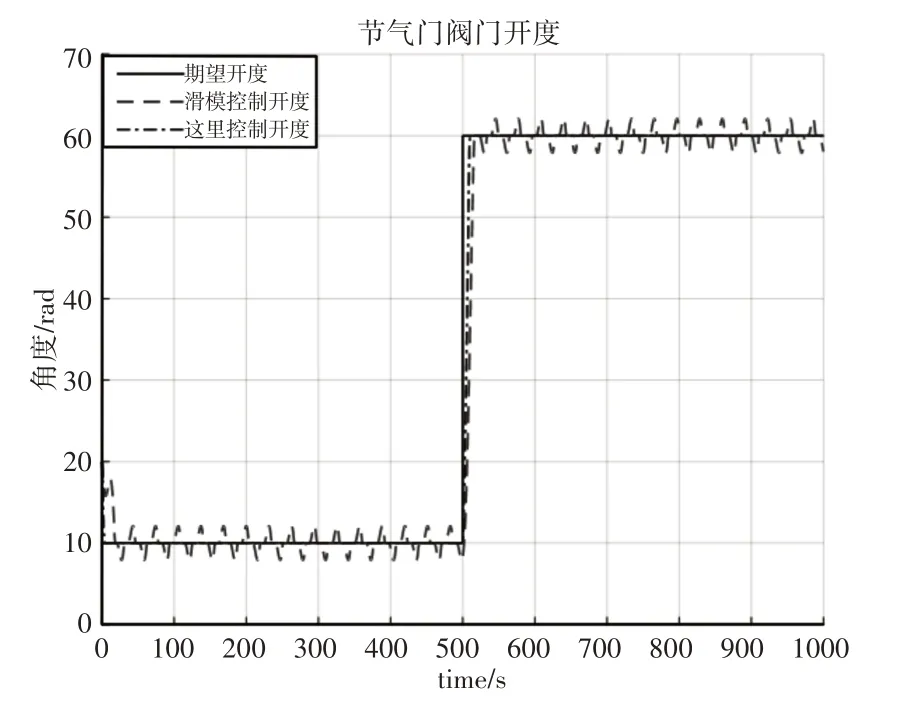
图5 节气门阀门开度跟踪Fig.5 Tracking of Throttle Valve Opening

从图5可以看出，这里所提控制方法能够控制节气门阀门开度从初始开度20rad迅速运动至目标阀门开度10rad，在t=500ms时，目标阀门开度阶跃至60rad，控制器同样能够控制节气门阀门开度迅速进行跟踪。同时从图6的跟踪误差图可以看出，除初始误差和阶跃短时间的跳动误差较大外，其他时间的跟踪误差均很小，而传统滑模控制方法则始终存在范围为（-3～3)rad的波动误差。该组实验对比结果证明了，这里所提控制方法能够克服传统方法无法解决的参数不精确带来的影响，实现高精度的角度跟踪控制。

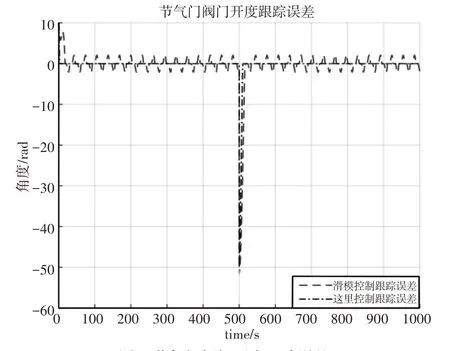
图6 节气门阀门开度跟踪误差Fig.6 Tracking Error of Throttle Valve Opening

从图7中可以看出，由于初始阀门开度大于期望阀门开度，这里所提控制方法能够控制节气门阀门以-4rad/s的初速度迅速运动使其达到目标开度，而后速度保持为0rad/s。当跟踪信号发生阶跃，即阀门速度发生跳变时，控制器能够控制节气门阀门开度从0rad/s提升至7rad/s并迅速恢复至0rad/s，并从图8的角速度跟踪误差图可以看出，除初始误差和阶跃短时间的跳动误差较大外，其他时间的跟踪误差均很小，而传统滑模控制方法则始终存在范围为(-2～2)rad/s的波动误差。该组实验对比结果证明了，这里所提控制方法能够克服传统方法无法解决的参数不精确带来的影响，实现高精度的角速度跟踪控制。

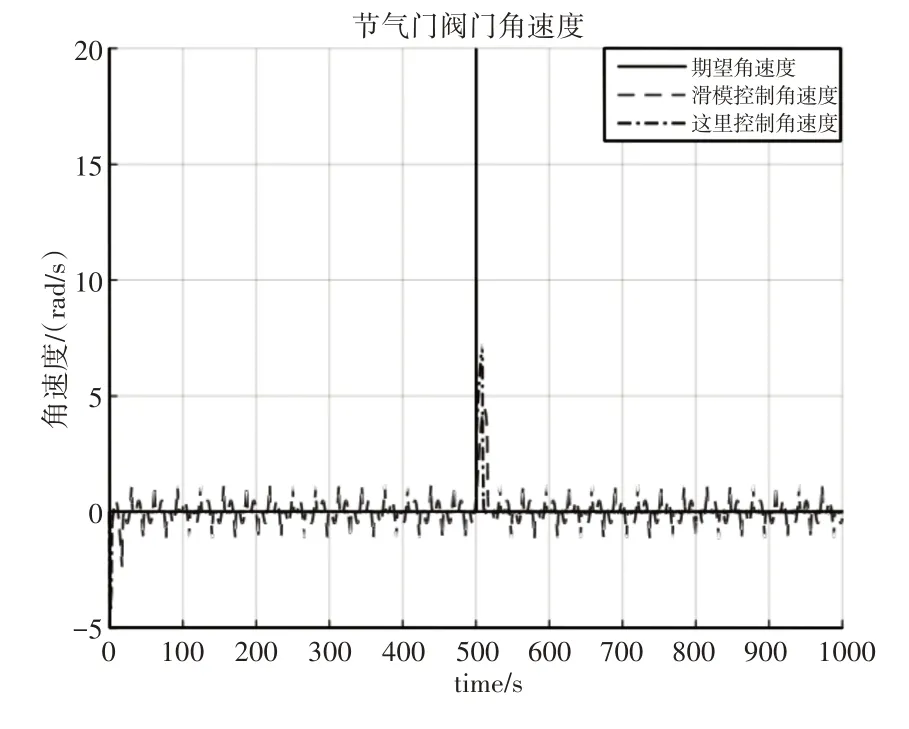
图7 节气门阀门角速度跟踪Fig.7 Tracking of Throttle Valve Angular Velocity

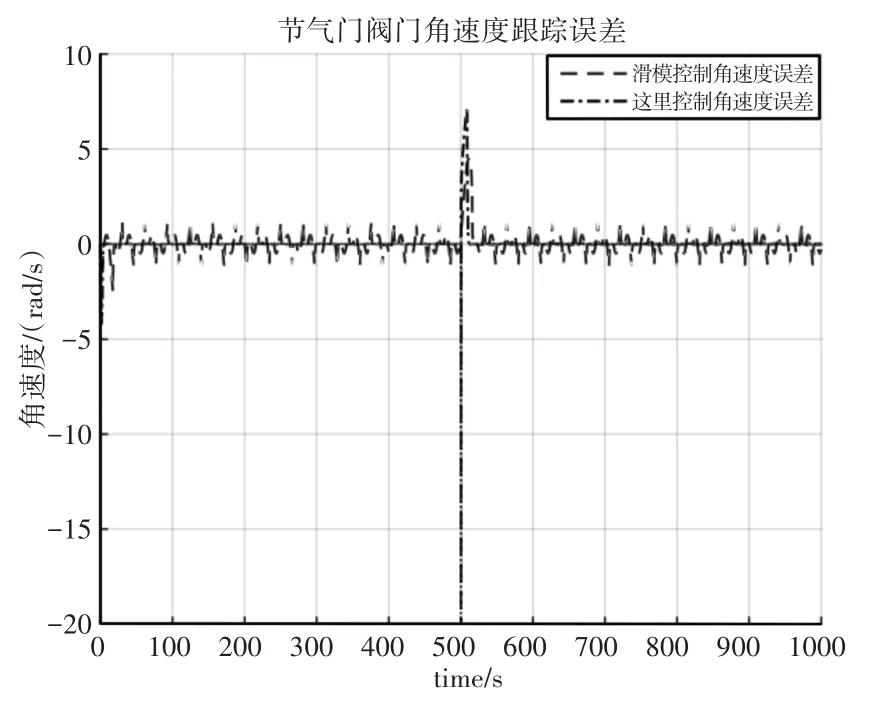
图8 节气门阀门角速度跟踪误差Fig.8 Tracking Error of Throttle Valve Angular Velocity

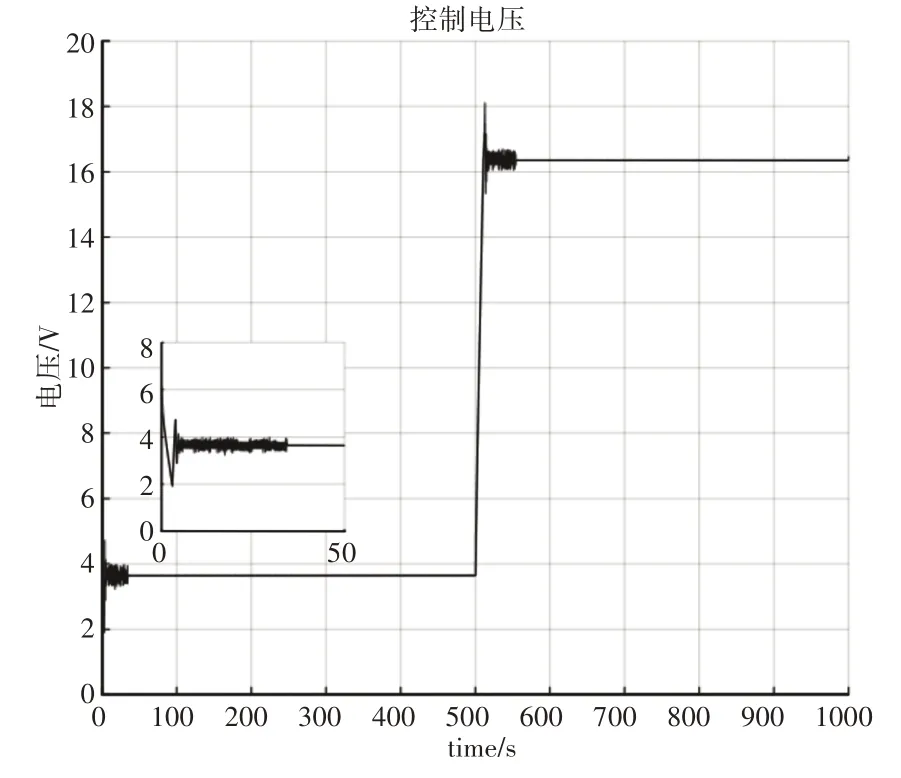
图9 节气门控制电压Fig.9 Throttle Control Voltage

从图9中可以看出，在t=10s左右时间内，节气门阀门开度从初始开度降低至目标开度，控制电压从u=6V 迅速下降u=2V，随后阀门目标开度稳定，控制电压经短时间震荡后随之稳定在u=3.7V；当时间运行至t=500s时，期望阀门开度迅速阶跃提升至θ=60rad，此时控制电压也随之提升至u=18V，随后阀门目标开度稳定，控制电压经短时间震荡后随之稳定在u=17V。该实验结果证明了所提控制方法的输出变量与实际阀门工作状态相符，同时能够满足实际工程需要。

综上，这里所提的神经网络控制方法，能够在存在外部扰动以及模型参数不精确的不确定条件下，实现电子节气门角度以及角速度的高精度跟踪控制，同时保持控制电压满足实际工程需求。

5 结论

当前大量对电子节气门控制问题研究中，均未考虑模型误差带来的不确定性，针对这一问题，这里基于传统滑模控制理论，利用RBF神经网络对建模不精确部分进行在线逼近，进而，提出一种自适应神经网络控制方法，并采用电子节气门典型阶跃开度信号进行了对比仿真实验，表明这里所提控制方法能够有效的对模型不精确部分进行在线逼近，从而补偿传统滑模控制器无法解决的跟踪误差，实现阀门实时开度对目标开度的精准跟踪。