改进人工鱼群算法在冷连轧负荷分配优化中的应用

张瑞成，孙玉辉，梁卫征，周亚罗

（华北理工大学电气工程学院，河北 唐山 063210）

1 引言

在冷连轧生产过程中，制定合理的轧制规程是一个重要环节。负荷分配作为轧制规程的核心，它的优化直接关系着冷连轧带钢的生产过程和质量。因此，如何快速优化冷连轧负荷分配具有重要的意义。

轧制负荷分配从早期的经验法、能耗曲线法等传统分配方法，渐渐发展到近年来的遗传算法、群智能算法（如蚁群、粒子群和鱼群等）、神经网络等人工智能优化算法。与传统分配方法相比，人工智能算法在优化轧制负荷分配方面对数学模型的精确性要求不高，易得到最佳负荷分配。文献［1］以轧制力成比例为目标，采用改进交叉算子和变异算子的自适应遗传算法，收敛更好、精度更高。文献［2］提出了基于高度因子的粒子群算法来对三个冷连轧负荷分配目标函数进行寻优，提高了算法跳出局部最优的能力。文献［3］以最优板形和凸性为目标，采用顺序无约束极小化技术将边界条件转化为无约束条件，然后应用粒子群优化算法对冷连轧机各机架轧制负荷进行智能分配，达到理想板形的要求。文献［4］将遗传算法和变尺度相结合，构成变尺度遗传算法来优化负荷分配，优化后的总轧制力比经验法的总轧制力小。

由上可知，智能优化算法在冷连轧负荷分配优化中起着重要作用。通过对智能算法的深入研究比较［5］，针对遗传算法容易陷入早熟，粒子群算法陷入局值难以跳出，蚁群算法初期搜索盲目性大的问题，选取了人工鱼群算法来优化轧制负荷分配。同时，针对人工鱼群算法后期收敛速度慢、结果精度低等问题，深入研究了他人对人工鱼群算法的改进［6-8］。文献［6］提出一种自适应视野和步长的混沌人工鱼群算法，解决基本人工鱼群算法易陷入局部最优的同时大大增加了算法的复杂性。文献［7］在基本人工鱼群算法中引入自适应视野和自适应拥挤度因子，提高了收敛精度，然而收敛速度并未提及。文献［8］采用加权质心人工鱼群算法以及自适应步长，具有较高的收敛精度和收敛速度，然而有时会陷入局部最优。鉴于以上研究，优化轧制负荷分配时，在引入基本人工鱼群算法的基础上，对其觅食行为的视野和步长先给定一个较大的值，然后引入衰减因子、截止因子和视步联合系数，使视野随着算法迭代逐渐减小，同时使步长依赖视野并随视野的减小而同比例减小，最后通过仿真实验验证了这一方法的可行性。

2 轧制目标函数及约束条件

轧制负荷分配优化即确定一组出口厚度使冷连轧机获得最优。条件不同，最优的目标也不同，所以最优是有一定的相对性的。根据冷连轧生产特性，常用的目标函数有等功率裕量目标函数、等压力目标函数、等主负荷目标函数［9］93－95和轧制力成比例目标函数［10］等，以及混合的多目标函数。以五机架冷连轧机为对象，综合考虑，为使设备能力得到充分发挥，采用轧制力成比例分配方式，即：

式中：Pi—第i机架的轧制力；ai—第i机架的轧制力比值。

2.1 轧制目标函数

为了确保带钢板型良好，对末机架（第5机架）的压下率进行了限定，使其压下率保持固定值。以第1到第4机架轧制力成比例分配的目标函数为：

式中：Qmin—轧制力成比例分配的目标函数；

Pi—第i机架的实际轧制力；

ai—第i机架的轧制力比值。

其中，轧制力模型为：

式中：B—带钢宽度—接触弧长度；QP—应力状态系数；KT—张力影响系数；K—材料强度；μ—摩擦系数；ε—相对变形程度；R—轧辊半径；R′—轧制压扁半径；h—轧出厚度；Δh—绝对压下量；σ—变形抗力。

轧制负荷分配优化的目标是：在已知第5机架的压下率和前4个机架轧制力比值的前提下，计算前4个机架的轧制力，使其比值尽可能接近设定好的比值。

为了满足大规模生产的需要，往往根据经验和以往轧制情况，记录下轧制质量较好时的各机架轧制力比值，并制成表格存储下来，以便轧制相关带钢时使用。

2.2 约束条件

在实际工程中，各个参数的取值都限制在一定的范围内，这种限制就是约束条件。根据轧机设备的不同或者轧制品种的不同，约束条件也不相同，而且，约束条件也并非必要条件，但是它对优化负荷分配的合理性起着重要作用。因此，可根据工程需要，选择合适的约束条件。

以压下率为考虑对象，选择了压下率约束条件，即：

式中：εi—第i机架实际的压下率；

εimin、εimax—第i机架允许的最小、最大压下率。

第一机架的来料厚度会产生波动，优化轧制负荷分配时要考虑到消除此波动，而且末机架要考虑到板型的良好，因此每个机架的压下率要限制在一定的范围内。

3 改进人工鱼群算法

人工鱼群算法是一种新型智能优化算法。基本人工鱼群算法是一种较好的寻优算法，但多次仿真会发现算法收敛速度慢，且易陷入局部极值难以跳出。通过分析各种参数对收敛性的影响可知，对于固定的视野和步长，无论过大还是过小，都会导致算法收敛速度减缓。因为觅食行为作为算法收敛的基础，对算法寻优发挥着重要作用，所以改进人工鱼群算法的基本思想是：聚群行为和追尾行为的视野和步长保持不变，只改进觅食行为的视野和步长。即在算法的初始阶段，给觅食行为一个较大的视野和步长，这样可增加全局的寻优能力，随着算法的迭代，视野和步长也在逐步减小，到达某一值后不再变化。改进人工鱼群的具体算法如下。

3.1 觅食行为

为加快收敛速度，在觅食行为中引入视野衰减因子α，α是一个（0～1）之间且随迭代次数增加而减小的数。然而视野不能一直衰减下去，故又引入截止因子β，当α≤β时，视野不再衰减，此时视野为初始视野的β倍。

具体的算法表达式为：

式中：α0—衰减基数；

α—衰减因子；

k—迭代次数；

Visual0—初始视野；

β—截止因子。

取α0=0.84、β=0.3进行仿真实验。

同时每次迭代时，觅食行为中的步长也随视野变化而变化，故可设定一个由Visual和Step相关的视步联合系数φ。具体的算法表达式为：

式中：k—迭代次数；

Step0—初始步长；

Visual0—初始视野；

φ—视步联合系数，且φ在（0～1）之间。

取φ=0.8进行仿真实验。

人工鱼Xi在其视野内随机选择一个状态Xj，即：

式中：Visual—视野范围，Rand()函数产生（0～1）的随机数。

分别计算Xi与Xj的目标函数值Yi与Yj。如果食物浓度（极小值问题）Yi>Yj，则Xi向Xj方向移动一步，即：

式中：Step—移动步长。

否则，Xi在其视野内选择一个新状态Xj，判断是否满足前进条件，若尝试尝试Tray-number次后仍不满足前进条件，则执行随机行为。

3.2 聚群行为

人工鱼Xi搜索视野内伙伴数目nf和中心位置Xc，若<δ（其中n为种群数目，δ为拥挤度，0 <δ<1），则中心位置Xc周围不拥挤，Xi向Xc方向移动一步，即：

否则执行觅食行为。

3.3 追尾行为

人工鱼Xi搜索视野内伙伴函数Yj最优伙伴Xj，如果食物浓度（极小值问题）Yi>Yj，且<δ（0 <δ<1），则最优伙伴周围不拥挤，Xi向Xj方向移动一步，即：

否则执行觅食行为。

3.4 觅食行为

人工鱼在视野内随机移动，到达一个新状态，它是觅食行为的一个缺省行为。

即：

改进人工鱼群算法优化负荷分配的基本流程示意图，如图1所示。

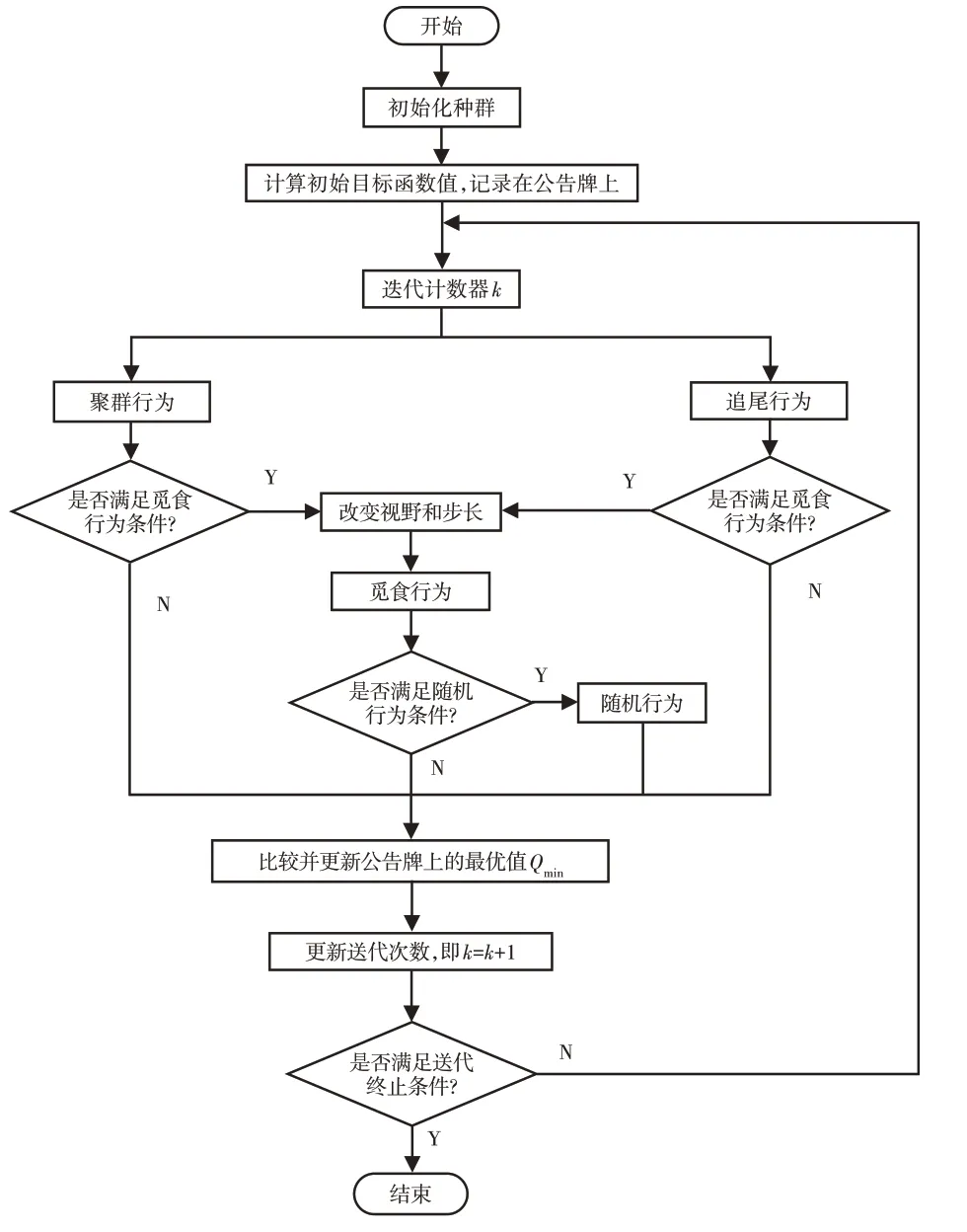
图1 改进人工鱼群算法的轧制负荷分配流程图Fig.1 Rolling Load Distribution Flow Chart of Improved Artificial Fish Swarm Algorithm

4 仿真分析

为了验证改进人工鱼群算法在优化轧制负荷分配上的合理性，以某钢厂五机架冷连轧机为例，在MATLAB仿真环境上进行验证。

4.1 参数设置

4.1.1 轧机参数设置

轧机各机架轧辊半径相同。选择钢种为Q235的带材来进行实验。其中第五机架采用固定压下率为5%，前四机架的轧制力比值分配比为［0.8906：1.019：1.000：0.990］［10］。相关轧制参数，如表1所示。

表1 轧制参数Tab.1 Rolling Parameters

4.1.2 改进人工鱼群参数设置

每个人工鱼为X=[h1h2h3]T，其中，h1、h2与h3分别为前3个机架的出口厚度。食物浓度为Y=Q，其中，Q为目标函数值。经过多次仿真实验，改进人工鱼群算法各参数的选取结果，如表2所示。

表2 人工鱼群算法参数Tab.2 Parameters of Artificial Fish Swarm Algorithm

4.2 仿真结果

在仿真过程中，记录每次迭代后的目标函数最小值，直至收敛，并记录下此时的最优解，并将改进人工鱼群算法与基本人工鱼群算法相比较。目标函数值随迭代次数增加而改变的情况，如图2所示。

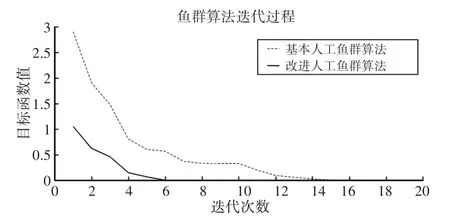
图2 基本人工鱼群算法与改进人工鱼群算法对比Fig.2 Comparison between Basic Artificial Fish Swarm Algorithm and Improved Artificial Fish Swarm Algorithm

由图2可以看出在用基本人工鱼群算法求解轧制负荷分配时，会陷入局部极小值，使程序运行时间增加。而改进人工鱼群算法求解轧制负荷分配时，则无此问题，可以很快收敛至全局最优，由图2可以看出，算法迭代（6～7）次时基本达到全局最优，此时目标函数值为6 × 10-5，用时1.47s。使用基本人工鱼群算法和改进人工鱼群算法优化轧制负荷分配时，最后求解出的最优解一样。典型轧制规程设定计算［9］106与基于改进人工鱼群算法求解的轧制负荷分配的对比，如表3所示。

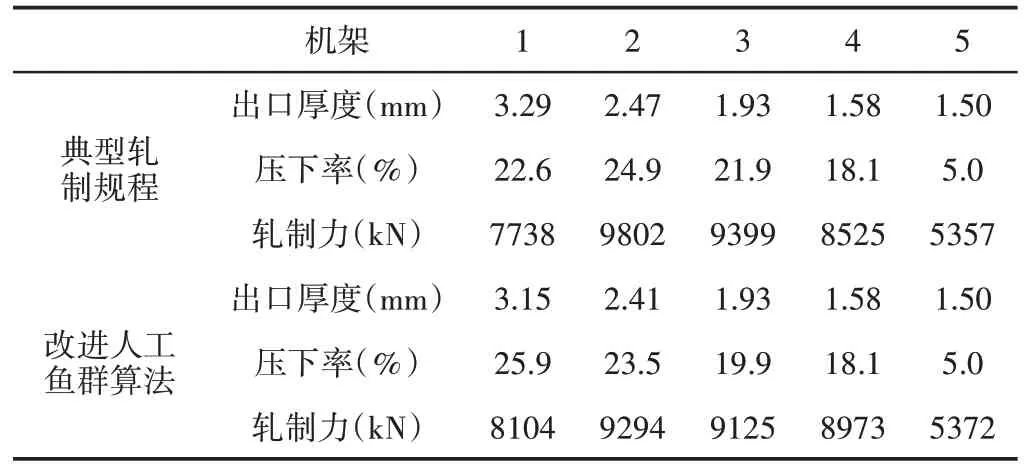
表3 典型轧制规程与改进人工鱼群算法优化的轧制负荷分配Tab.3 Typical Rolling Schedule and Rolling Load Distribution Optimized by Improved Artificial Fish Swarm Algorithm

由表3可以看出，基于改进人工鱼群算法优化的轧制负荷分配与典型轧制规程的各机架出口厚度相差不大，且经过计算可得各机架的两种规程得到的出口厚度误差最大为4.26%，且前4机架的轧制力比值为，与设定比值有细微差别，这是因为各机架轧制力只取整数部分以及目标函数值取不到0。第4和第5机架两种方法的入口厚度、出口厚度一样，而计算的轧制力不一样，这是因为两种方法的轧制力模型有细微差别，两种方法对应的轧制力误差最大为5.26%。以上实验结果，验证了改进人工鱼群算法优化轧制负荷分配的可行性。

5 结论

基于仿真分析，可以得到如下结论：

（1）使用基本人工鱼群算法对轧制负荷分配的优化是可行的，其结果与使用改进人工鱼群算法求得的结果一致，与典型轧制规程相差不大，相差在5%以内。

（2）使用基本人工鱼群算法收敛速度慢，且易陷入局部极值。而改进人工鱼群算法在优化轧制负荷分配时，不但很好地解决了上述问题，具有收敛速度快、不陷入局部极值的效果，基本2s左右即可收敛到最优值，而且算法简便，易于实现。

（3）人工鱼群算法对目标函数的要求不高，所以无论是基本人工鱼群算法还是改进人工鱼群算法，对于其它轧制目标函数或轧制规程都可以适用，扩展性强。