基于深度学习和贝叶斯优化的压缩机故障诊断

董丽娟，方 召，陈会涛

（1.许昌电气职业学院机电工程系，河南 许昌 461000；2.河南理工大学机械与动力工程学院，河南 焦作 454003）

1 引言

压缩机是工业中使用比较广泛的机器之一，然而，压缩空气的成本很高，因为只有19%的功率可用，而早期诊断故障对于防止压缩机工作效率降低，保证系统安全正常工作至关重要［1］。对各国往复式压缩机的消费者和制造商进行的一项调查显示，其机械系统的故障导致约76.5%的压缩机意外故障，其中阀门是往复压缩机中经常故障的部件之一［2］。

为了解决上述问题，开发了数据驱动方法来检测和诊断压缩机及其阀门的状态。这些方法使用传统的机器学习方法，包括特征提取、特征选择以及模式识别。针对振动信号特征提取问题，采用主成分分析和统计分析相结合的方法对往复式压缩机进行诊断［3］。文献［4］将Hermite 局部均值分解和多尺度模糊熵作为SVM分类器的输入特征，构建轴承间隙故障检测系统。文献［5］介绍了一种基于统计特征和决策树分类器的空气压缩机故障诊断方法。文献［6］基于时频特征和logistic回归的方法也被应用于压缩机阀门在低变工况下的裂纹检测。虽然上述方法表现出一定的诊断效果，但仍然存在两个显著的问题：（1）它们基于复杂的信号处理技术，用于转换不相关特征中的原始振动信号，这可能会丢失非平稳和脉冲信号的时间相关信息。（2）特征选择、分类阶段不能直接提取时间序列的特征，依赖于先验知识。

基于数据驱动技术的预测和健康管理任务中另一个重要问题是超参数优化。网格搜索和随机搜索、遗传算法（Genetic Algo‐rithms，GA）和贝叶斯优化（Bayesian Optimization，BO）等技术已经被提出来解决这个问题，例如，文献［7］提出了通过BO的支持向量机模型应用于工业测量数据分类。文献［8］提出了将BO与粒子滤波相结合的轴承故障特征提取方法。文献［9］提出了动态贝叶斯小波变换用于估算剩余使用寿命中的维护参数。通常，该类优化问题可以通过手动试验解决，但是由于高度依赖设计人员的先验知识，因此无法推广其应用。另一种方法是使用超参数配置来避免优化问题的解决，该超参数配置已经足够完成其他诊断任务。但是，它假定共享建模的过程属性，并且不能保证此假设的泛化能力。

针对上述问题，提出了一种基于深度学习和贝叶斯优化的压缩机故障诊断方法，通过时域计算短窗口的预处理方法降低模型复杂性，并且不损失时间相关信息。然后从压缩机振动信号的时间序列表示中迭代训练长短期记忆模型，在每次迭代中限定搜索空间，并利用贝叶斯优化方法对超参数进行优化。实验结果证明提出的方法能够显著提升故障诊断的性能。

2 基本理论

2.1 循环神经网络和长短期记忆网络

循环神经网络（RNN）是一种生物启发的计算模型，该模型由以下动力学系统表示：

向量h(t)保留由W矩阵加权的先前状态向量h(t-1) 的信息，并对Win进行了慎重考虑从而在当前输入x(t)中添加新信息。另一方面，向量(t)使用向量y(t)表示的Nout个互斥随机变量对多变量过程进行建模。因此，等式（2）表示具有Wout参数的soft‐max回归情况。特别地，f(⋅)通常是双曲正切函数，平滑地限定状态向量的值。

在RNN的训练阶段，通过一种优化算法对权值Win，W和Wout进行调整。LSTM神经网络是RNN衍生的计算模型，可以学习长期依赖关系。为此，状态向量是通过一个更新机制进行计算，该机制由式（3）～式（8）形式化：

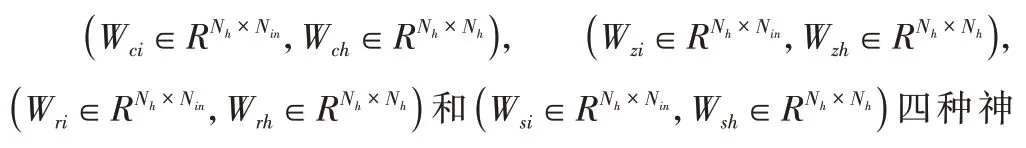
利用前面的术语可以构建深度学习模型，其中一组隐藏层{h1，h2，…，hnl}可逐步堆叠以增加生成模型的容量。

2.2 贝叶斯优化

BO方法是优化不可微、不连续和高成本功能的工具。它在模型选择中的使用在基于序列模型的优化（SMBO）算法中被形式化，作为其应用的一般框架。

ϕ和p(error|ϕ)分别是模型ℳϕ的一组超参数和给定一组超参数的模型错误的概率分布。为了运行SMBO来优化ϕ，必须定义两个函数：目标函数f(μϕ)和采集函数S(ϕ，p(error|ϕ))。f(ℳϕ)函数评估ϕ参数化的模型误差，从而给出ϕ的性能度量。通常，此功能的评估成本很高；因此不可能对其直接最小化进行详尽的搜索。为了解决先前的问题，定义了S(ϕ，p(error|ϕ))函数，以便在搜索空间中找到更有利的探索区域。SMBO流程概述如下。

（1）初始化p(error|ϕ)模型。

（2）通过解决以下问题获得新的超参数集：

（3）通过f)计算。

（5）基于证据D，估计一个新的p(error|ϕ，D)模型。

（6）从2开始重复，直到达到最大迭代次数

函数f(⋅)依赖于应用超参数的特定模型，通常是要解决任务中的某些模型性能度量。对于p(error|ϕ)模型估计，生成模型p(error|ϕ)通过贝叶斯规则估计。

生成模型p(ϕ|error)由两个密度函数组成，即：l(ϕ)和g(ϕ)。从D中的实例获得l(ϕ)函数，并在误差阈值内评估f(⋅)，并从D的其余实例计算g(ϕ)：

其目标是将D中的实例最大化来计算函数l(⋅)，将实例最小化来计算g(⋅)。然而，最后一种算法在迭代优化的每一步都提高了搜索空间的多样性。负期望改进（NEI）通常用于函数S(⋅)，该函数与等式（11）相结合得出等式（12）：

式中：γ—由D得到的f的下分位数。

3 提出的方法

3.1 基于时间指示的信号预处理

在给定信号的训练，验证和测试集的情况下，属于这些集之一的原始信号通常由大量样本组成。例如，对于采样频率为fs=50000samples s，10s采集时间内，将获得500000个样本的信号。直接将这些长信号用作输入来生成深度学习模型（例如LSTM）会产生过多的计算负担。为了解决上述问题，对数据集中的每个信号提出了下一步的预处理过程。

令x为长度为T的信号。令sw和Δ为选择窗口的长度和sw的步长增量。计算L，即信号x中的迭代次数，为：

对于l，从0到（L -1）：提取要处理的选定信号z，如下所示：

对于z，计算J条件指示器并将其保存为向量CI。将低速率信号的第l个元素赋值为=CI。

上面的过程适用于序列，验证测试集中的信号。这一阶段的核心是在子信号z上提取一组J状态指示器CI。比较了用于旋转机械故障诊断的不同统计特征。CI通过选择具有以下特征的条件指标来限制计算时间：（1）O(1)：常数的计算复杂度；（2）O(n)：线性计算复杂度；（3）计算的CI。因此，得到下11个CI：

式中：CI0，CI1，…CI10—平均值，均方根值，标准偏差，峰度，峰值，波峰因数，校正平均值，形状因数，脉冲因数，方差和最小值。

然后使用均值归一化将每个低速率信号的数据缩放到一个正态标准分布假设，为了避免基于神经的模型的单位饱和。扩展的步骤如下：

计算训练集中j=[0，J-1] 的经验均值和标准差。在训练，验证和测试集中的x低速率信号中按比例缩放每个维度，如下所示：

数据集中每个信号的缩放会导致标准化和集。

最后，训练集的大小在建立深度学习模型中起着至关重要的作用，但是这个大小对于获取阶段的实验负担是有限的。然而，在研究中，压缩周期时间通常比信号长度小得多。为了增加每个标准化数据集中的信号数量，进行了如下改进：

（1）设cw为得到的信号的长度

（2）对于i，从0到L-cw-1：

3.2 基于超参数贝叶斯搜索的LSTM模型

预处理过程，如图1所示。在经过时间阶段的状态指标提取之后，原始振动信号由11维时间序列表示，其长度比原始时间短得多。然后再进行缩放，最后通过信号切割来增加数据集。根据图2所示的架构，通过预处理获得的信号集中的每个信号都会通过LSTM模型。用于训练该体系结构的超参数将被优化，以获得用于诊断任务的最佳模型。

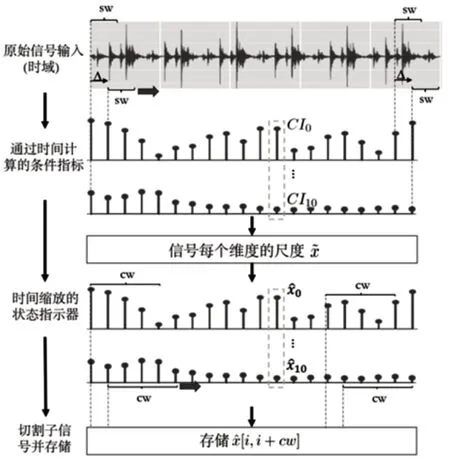
图1 预处理过程Fig.1 Pretreatment Process

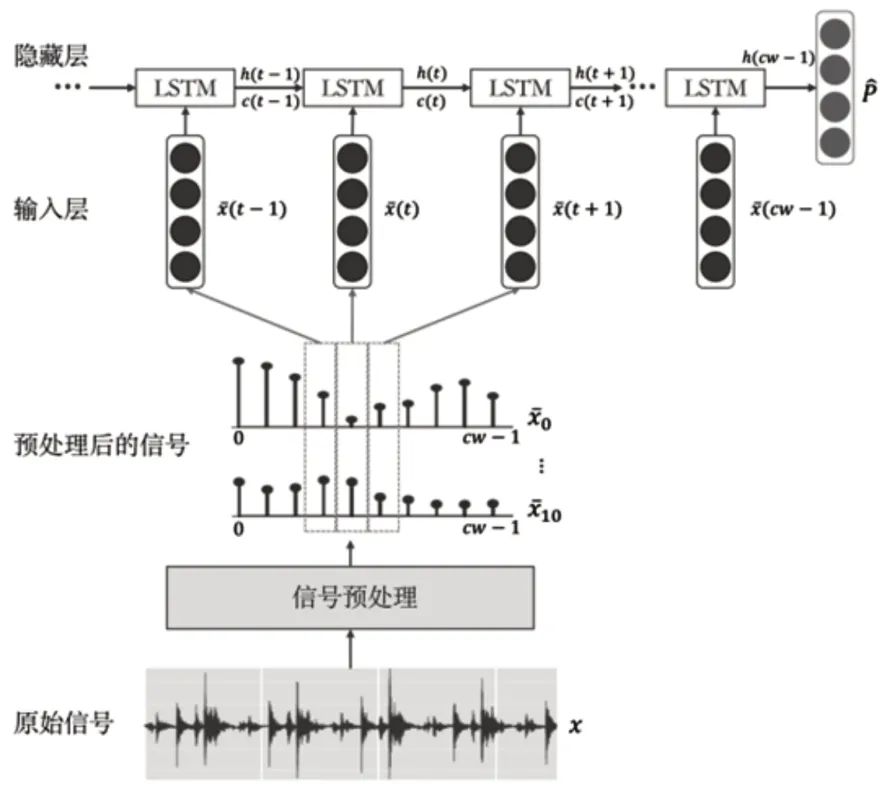
图2 故障诊断架构Fig.2 Fault Diagnosis Architecture

设X和V分别为预处理得到的训练集和验证集。并且设ℳh为通过使用X和一组超参数h∈ℋ建立的基于LSTM的模型。

集合h具有以下超参数：学习率(lr)，层数(ln)，单位数或隐藏神经元的数量(nu)，学习率(lr)和批大小(b)。它们是从ℋ搜索空间中绘制的。令f(μh)为目标函数，其能够评估集合V中模型的诊断误差。

超参数优化任务描述为如下优化问题：

这里提出在基于LSTM 的诊断模型的训练循环中使用BO来解决等式（30）中引入的问题，即每次迭代提供的信息会降低计算复杂度。要优化的函数f(⋅)是模型的误差分数，可以通过计算得出：

式中：Pi和—正确的故障模式和估计的故障模式，并且1(⋅)是指标函数，如果参数为true，则值为1，否则为0。每个超参数都有一个与超参数空间的先验知识相关的先验分布。为指定的间隔和增量定义了离散的均匀分布，该分布并不优先考虑某些值，但对数均匀分布是连续的，它优先考虑在学习率超参数中通常出现的最小值附近的值［10］。

3.3 故障诊断模型

前面通过超参数优化过程构建的详细故障诊断模型，如图3所示。可以归纳如下：

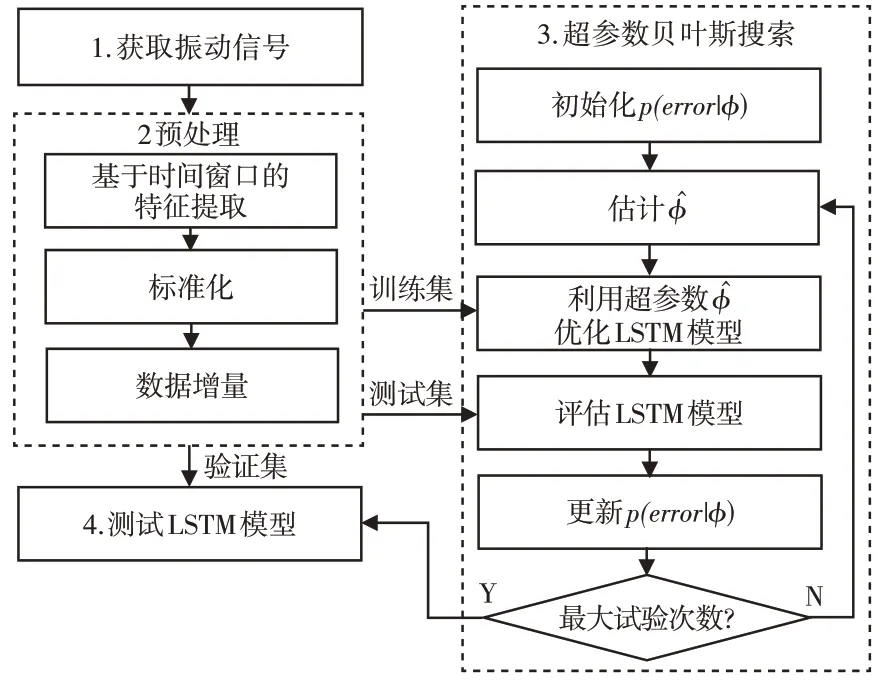
图3 故障诊断算法Fig.3 Fault Diagnosis Algorithm

（1）通过第3.1小节中详细介绍的过程在时域中提取条件指标。从这个阶段的结果来看，X和V数据集被用于构建模型。

（2）根据3.2 小节中详细说明的过程，迭代地执行超参数优化。在此阶段，使用集合X和Adam算法训练LSTM模型。

（3）使用带有V集的f(⋅)函数对训练好的LSTM进行评估，每次迭代的结果都是一个新的得分值，用于获得下一组超参数。

（4）从第（2）步开始，重复进行20次实验确定的迭代，以使优化过程收敛。

（5）选择使式（30）最小的。

true positivesk(tpk) ：被模型正确地识别为故障模式k的故障模式k的样本百分比。

false negativesk(fnk) ：模型错误地将故障模式k的样本百分比标识为另一种故障模式。

false positivesk(fpk) ：被模型错误地标识为非故障模式k的非k故障模式的样本百分比。

true negativesk(tnk) ：模型正确地将非k故障模式的样本百分比标识为非k故障模式。

precisionk：模型避免将非k个故障模式样本错误分类为故障模式k的能力：

recallk：该模型避免将错误模式k个样本错误分类为非k个错误模式的能力：

fscore，k：精度和召回率之间的权衡：

accuracy：模型成功和错误的比率。衡量模型在K个故障模式下的总体性能的指标是：

4 实验装置

4.1 试验台

实验在压缩机试验台上进行。250 EGB 的两级压缩机由5.5hp 感应电动机驱动，提供57.7Hz的旋转运动，该运动通过两条V型皮带传输至压缩相机，垂直放置的加速度计型号为PCB 603C01 的压缩相机。模拟信号通过电线传输到NI 型号为NI9234 的紧凑型数据采集卡（cDAQ），该卡专门用于振动测量。该卡负责按所需的采样频率进行模数转换。cDAQ 连接到NI9188 机箱上，通过100mbps 的以太网链路将数字信号传输到笔记本电脑上。在LabView 软件中实现了一个采集系统来控制整个数据采集过程，每个捕获的信号都存储在硬盘上进行预处理。

往复式压缩机有两个压缩阶段，选取各压缩阶段的进、排气阀作为研究单元。这些组件被人为地操纵以配置每个阀门的五种状态：（1）健康状态；（2）阀座磨损；（3）阀板腐蚀；（4）阀板裂纹；（5）春假。模拟故障，如图4所示。总共生成了17种机械条件，详细信息，如表1所示。

表1 健康状况和模拟故障模式Tab.1 Health Status and Simulated Failure Modes

图4 故障模式Fig.4 Fault Mode

在恒定的57.7Hz电动机旋转频率下进行测量，得出曲轴旋转频率为12.8Hz。因此，总压缩周期消耗大约0.156s（每个压缩周期2个曲轴周期）。储罐压力保持恒定在3bar。每台机器工况采集15个振动信号，采集时间为10s，随机采集间隔为（10～60）s。共获得255个测量信号（17种故障模式，15次重复）。每个信号都以50 kHz的采样频率进行数字化，根据采样定理［11］，它可以获得高达25kHz的频率信息。

产生的信号集被分为三个子集，分别称为训练集，验证集和测试集，分别包含70%，15%和15%的信号。前两组用于训练阶段，以建立计算模型，最后一组用于测试模型。为避免模型建立或试验时的偏差，采用随机抽样和机械条件分层的方法进行分离。

不同阀瓣阀座磨损对应的振动信号样本，如图5所示。快速傅里叶变换计算出的振动信号频谱，如图6所示。正常情况的频谱在其较低的频带（0～7500）Hz提供信息。由于机器上的零件的运动是较慢零件的运动的倍数，因此它会在较高的频带中复制。同样，某些频率成分归因于谐波。在图5（b）中可以看到幅度略有减小，但其形状得以保持。尽管这些信号来自机器的不同条件，但在图6（a）、图6（c）所示的信号之间可以观察到形状和幅度的显著相似性。另外，不可能在时域或频域中为每种条件在信号中找到可识别的模式。这一事实导致在简单地观察原始信号或其光谱的基础上辨别机械状态的复杂性。

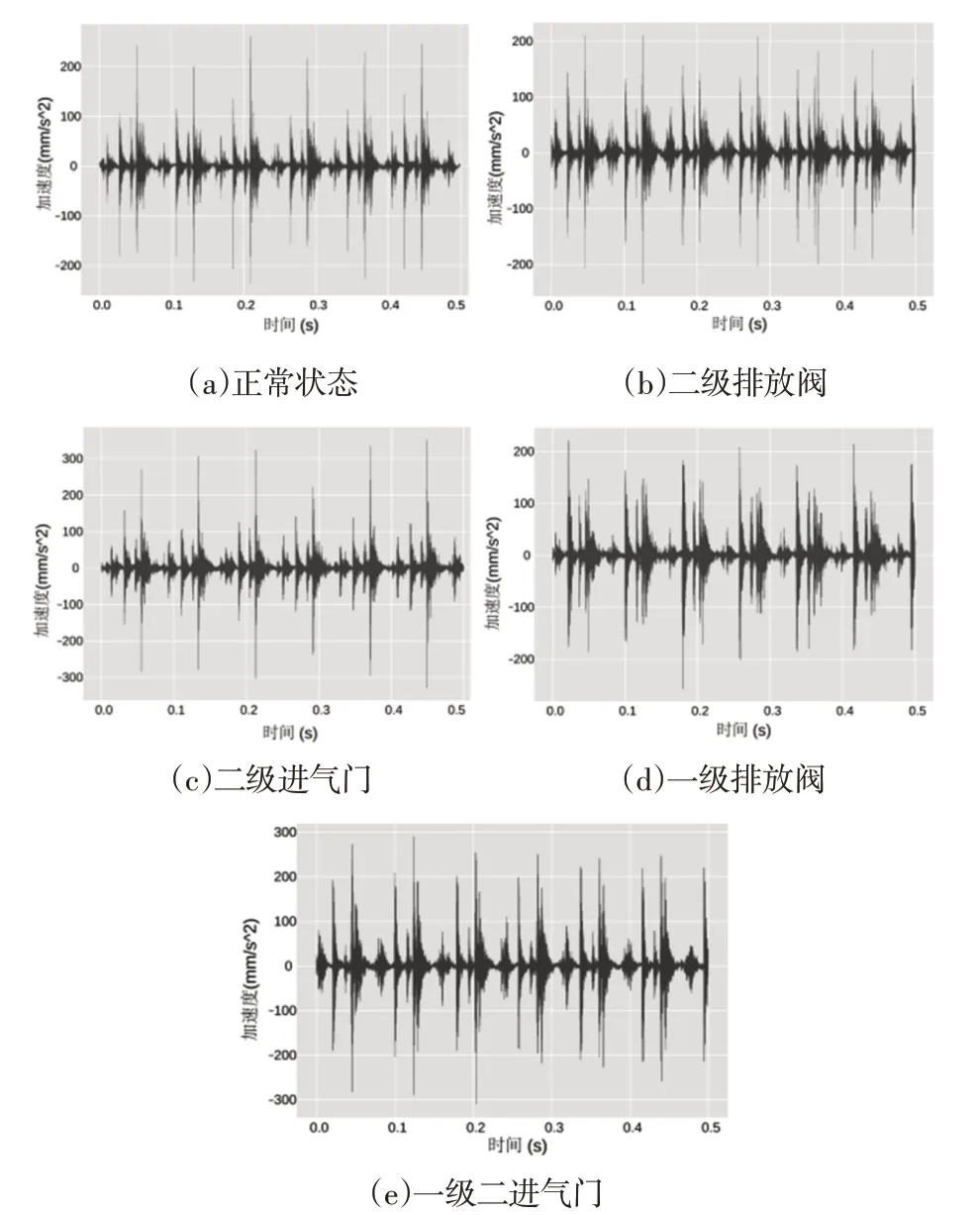
图5 不同部件阀座磨损阀故障的振动信号Fig.5 Spectrum of Vibration Signals of Seat Wear Valve Fault in Different Components

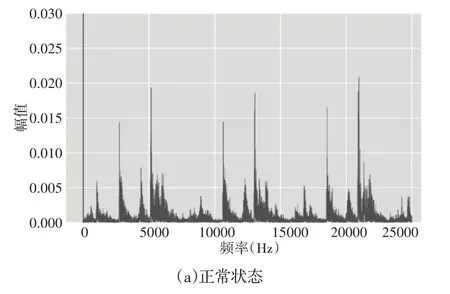
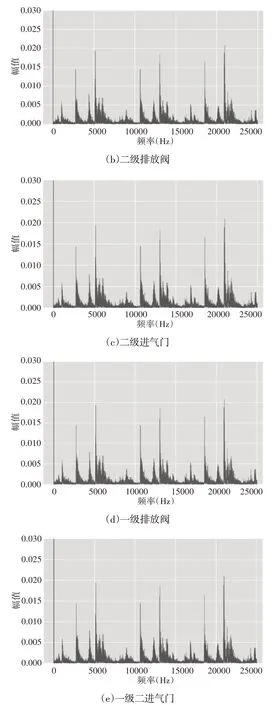
图6 不同部件阀座磨损阀故障振动信号的频谱分析Fig.6 Spectrum of Vibration Signals of Seat Wear Valve Fault in Different Components

4.2 实验比较方案

采用该方法进行了60组实验，以评估不同预处理参数配置下LSTM模型选择过程的性能。每个参数使用的值，如表2所示。在所有的实验中，对于预处理参数的每一个构造，基于Adams的LSTM训练阶段都设置为200次迭代，并获得在该区间内误差最小的迭代模型。为了进一步评估这里的方法，这里将对经典方法和基于下一个模型的深度学习方法进行了比较，并进行了详细的配置和/或优化。

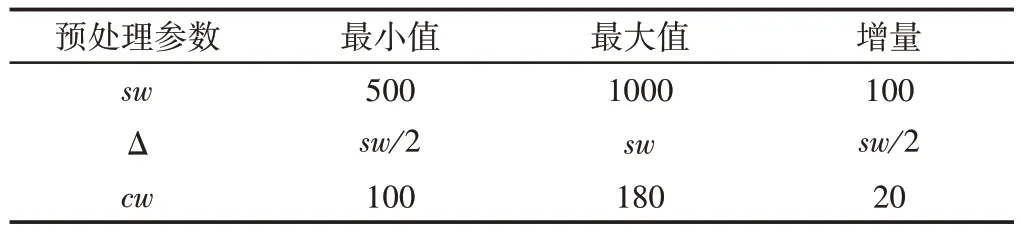
表2 预处理参数的间隔时间Tab.2 Interval Time of Pretreatment Parameters

随机森林（RF）［12］：拟议分割的候选特征数量为log2(F)，其中F是数据集中特征的总数。每棵树的深度都增长到在最后一个节点中只有一个实例。树的数量在（2～1000）之间，其中，50是最优值。

分类树（CART）［13］：使用CART算法来分割节点。分割候选特征的数量设置为F。树的深度是最大的。未执行任何修剪。

k-近邻（KNN）［14］：将输入特征的数量设置为F。相邻节点的数量在1到100之间进行评估。只有一个邻位时，性能最好。

长短期记忆（LSTM）［15］：这里在研究案例中采用了中提出的方法。将500000 个采样长度的振动信号分为50 个信号，每个10000个采样。将每个信号都转换为（100×100）矩阵，其中的列代表时间步长，而行是要在每个时间步长中输入LSTM 的要素。这里将学习率设为0.007，隐层数为2，每层单位为50，训练算法为自适应梯度。G-LSTM：此模型是通过应用这里提出的方法来优化LSTM超参数而创建的。搜索空间的离散分区如表1所示，不同之处在于学习率的离散化为0.02。生成的超参数为b=8000，lr=0.081，nl=2和nu=16。

去噪自动编码器（DAE）：遵循从原始数据提取深度特征的相同思路，将DAE方法与这里的方法进行了比较。该模型通过对编码器网络的学习，建立了一组深度特征。此外，还利用解码器网络将特征转换为原始输入。将两个网络一起优化，以最小化模型输入和输出之间的差异。

输入是根据第3.1 节预处理的信号。该模型的超参数优化是通过Grid Search 执行的，获得了一个编码器网络，该网络具有4 个隐藏层，每层［500，350，270，100］个单元，每层破坏因子为0.3，学习率为0.0015，批处理大小为100和1500个单次训练迭代。

稀疏自动编码器（SAE）：这种方法遵循DAE的基本原则。然而，它的主要区别是包含了一个正则化因子来保证网络权值的稀疏性。其输入与DAE相同。通过网格搜索获得的超参数为3个隐藏层，每层［500，750，930］个单位，稀疏系数为0.2，学习率0.002，批量大小为100和1500个单次训练迭代。

5 结果与分析

5.1 预处理和贝叶斯优化

总结了sw和cw参数对性能的影响，如图7所示。通过确定待分析的预处理参数，改变其他参数，得到相应的误差向量，计算每个箱线图；例如，通过将sw固定在500，改变cw和Δ在各自的间隔内，可以得到一个10维误差向量。首先，sw的增加会导致误差变异性的降低，即在1000 个误差样本下，误差变异性会收敛到0.16 左右的均值。sw和Δ 最显著的发生率出现在较小的值，即500和600处，误差较低，分别为0.09和0.088。再看cw，其发展趋势尚不清楚。同样，在具有较高变异性（160）的参数值处观察到较低的误差（0.085）。

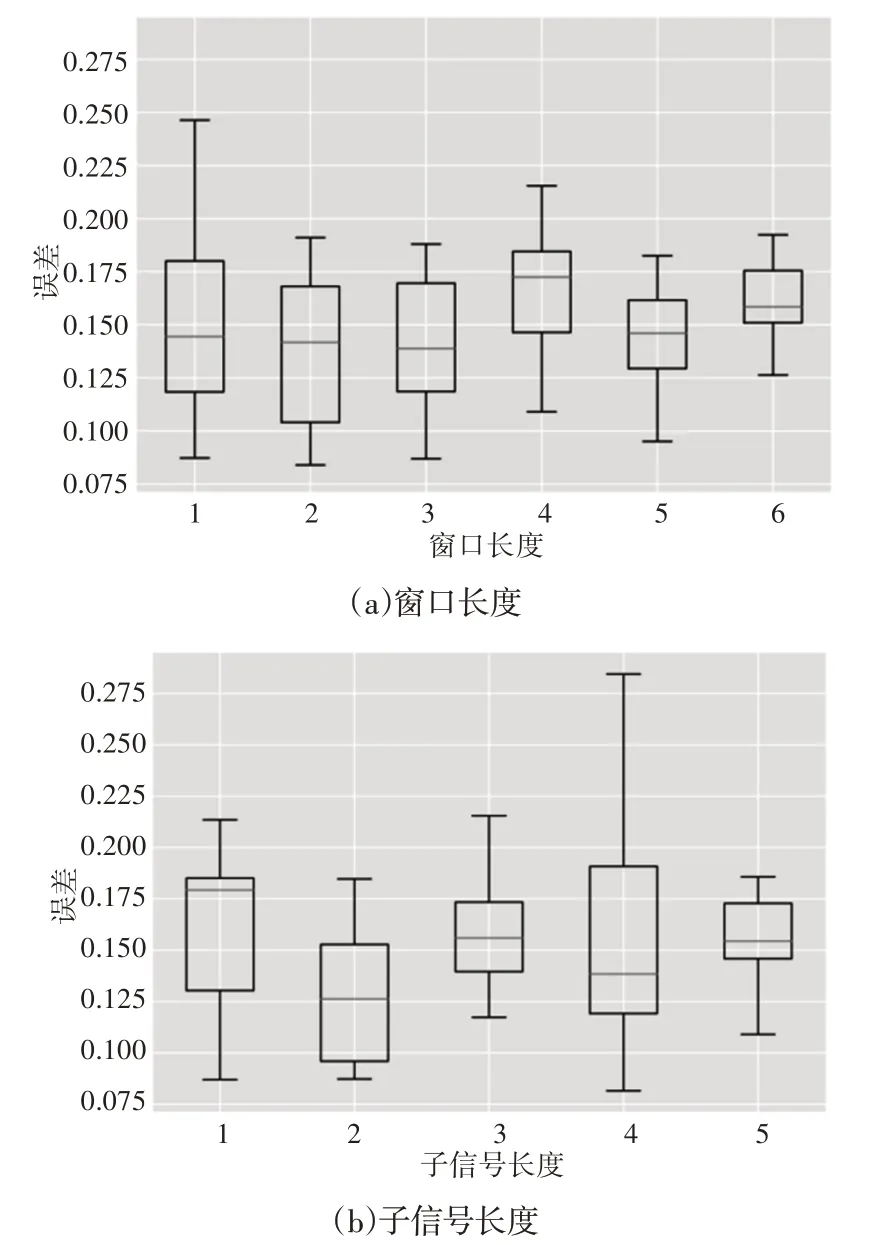
图7 参数对性能的影响Fig.7 The Influence of Parameters on Performance

为了进行更详尽的模型比较，从先前的结果中选择了表3中所示的五个最佳超参数集。五个最佳组合中的四个是从500或600的组合中获得的。此外，注意到三个超参数集（HP-1，HP-3和HP-5）共享b，lr，nl和nu的相同配置，证明了这些值的偏好，与预处理参数无关。

5.2 用于模型验证的统计测试和性能度量

对表3中的超参数构建的精细模型进行了比较。考虑到基于神经网络的模型对其初始重量配置的敏感性，为每个HP-i生成了十个模型，并评估了其在测试集中的准确性。

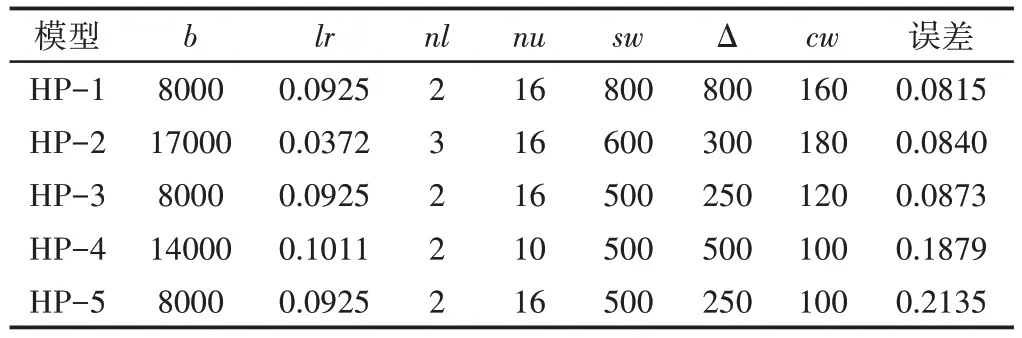
表3 选定的最佳超参数组进行比较Tab.3 The Best Super Parameter Group Selected for Comparison

Kolmogorov-Smirnov 检验的p值在0.05的显著性，其中所有模型的假设（>>0.05）都是显而易见的。高斯行为可以根据平均精度（avg 精度）和标准偏差（std）来描述结果。在所有情况下，LSTM模型的平均精度都超过了0.901，最大变异性为0.027。最佳模型为LSTM-5，其精度最高，为0.930，变异性最小，为0.017。

表4和图8显示了平均值的差异。但是，仍旧不足以保证模型结果之间的统计差异。为了解决这个问题，通过获取表5中所示的p值，对每对模型的结果进行了t检验。根据这些结果，模型对（LSTM-1，LSTM-2），（LSTM-1，LSTM-3），（LSTM-1，LSTM-4），（LSTM-2，LSTM-4）和（LSTM-3，LSTM-5）在统计上具有相同的性能。最后一对模型显示出最佳性能，它们具有相同的超参数，但参数cw有所不同，LSTM-3为120，LSTM-5为100。但是，在表4所示的优化过程中，这些模型的误差之间存在很大差异，而LSTM-3模型仅具有200次迭代的优势。结果表明，200次迭代之间的快速收敛并不能作为选择最佳模型的依据。最后，对于最佳模型（LSTM-5），每种故障模式的精度precision、召回率recall和fscore，如表6所示。P5，P6，P7和P9的精度较低。这意味着在这些故障模式下，信号没有被正确地分类。P1的精度为0.94，在分离故障条件和健康条件方面表现出良好的性能。P1，P3，P7，P8和P9的召回率较低。这意味着来自这些故障模式的信号在其他机械条件下没有被正确地分类。

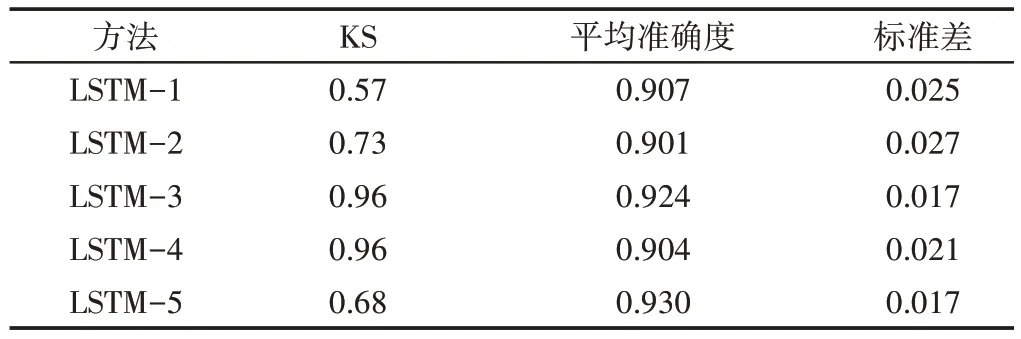
表4 每个LSTM-i模型的Kolmogorov-Smirnov（KS）检验和统计精度指标Tab.4 Kolmogorov Smirnov（KS）Test and Statistical Precision Index of Each LSTM-i Model

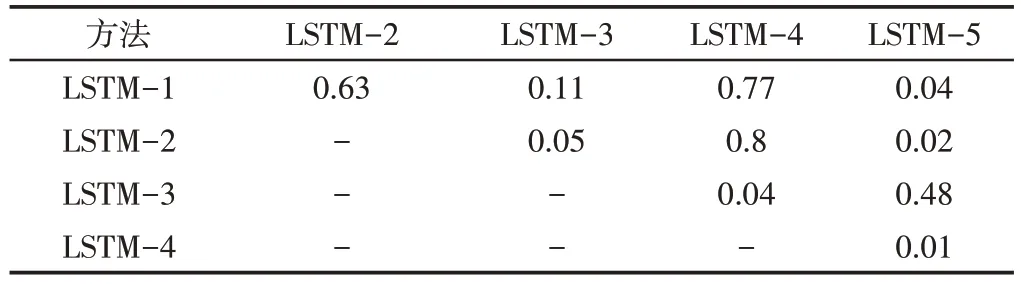
表5 模型对t检验的p值Tab.5 p Value of t Test

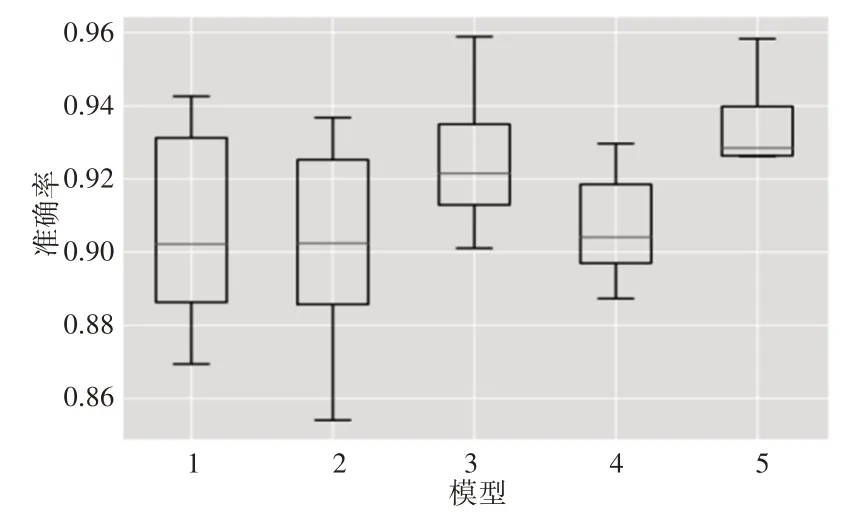
图8 最佳LSTM模型的比较Fig.8 Comparison of the Best LSTM Models

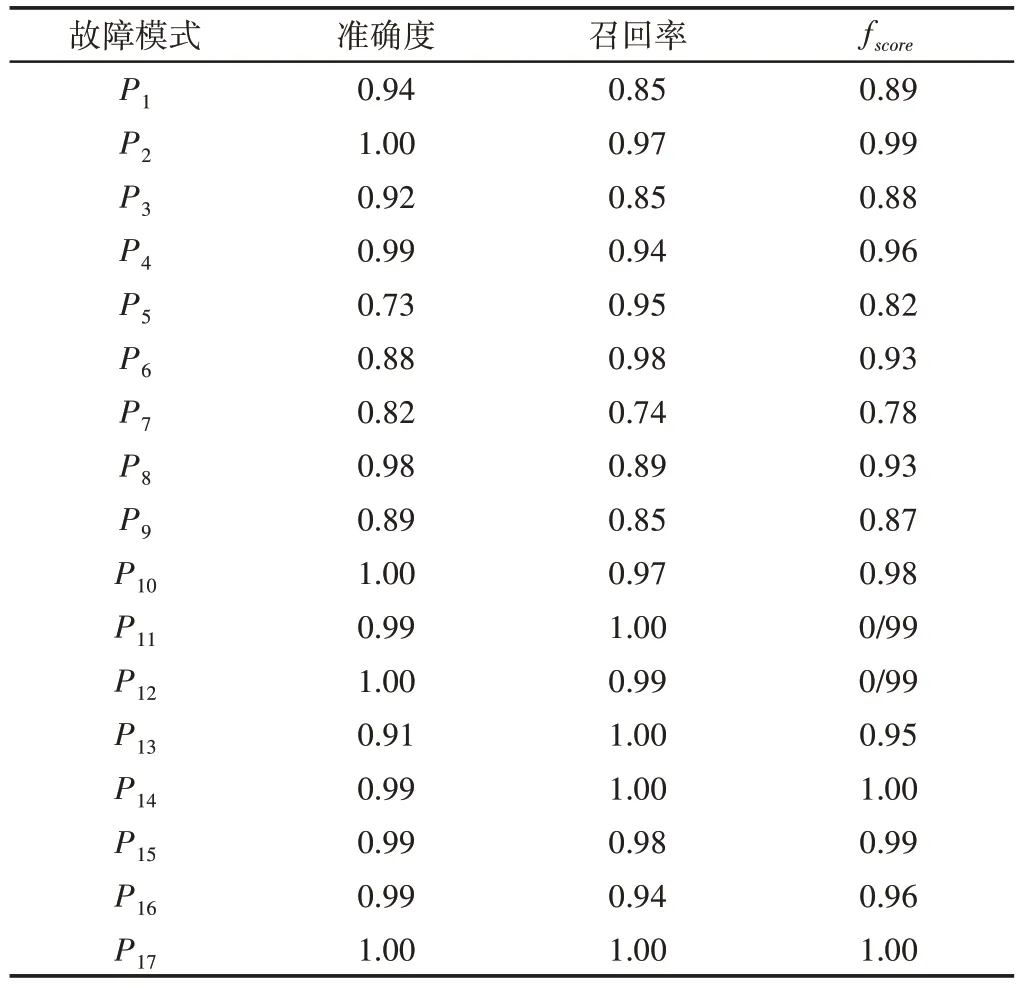
表6 最佳模型的评估结果Tab.6 Evaluation Results of the Best Model

5.3 方法对比

从表7所示的往复式压缩机诊断来看，与RF、CART和KNN相比，B-LSTM模型具有最好的分类率（93%）。当使用可以捕获时间相关信息的B-LSTM模型从时间序列表示中提取高级特征时，可以有效提高分类性能。LSTM模型的不良性能可能是由两个因素造成的：（1）缺乏计算能力，而在诊断压缩机中的17种故障情况时，每层需要更多层和单位；（2）高度依赖基于LSTM的模型的超参数调整。显然，所提出的预处理阶段在改进模型中起着至关重要的作用。但是，由于基于LSTM的模型可以自然地处理时间序列，因此DAE和SAE的性能比B-LSTM和G-LSTM差一些。B-LSTM相对于G-LSTM的精度优势是因为用网格搜索方法时假设的粗糙学习速率增量（0.02）。但是，较小的增量会增加计算复杂度。

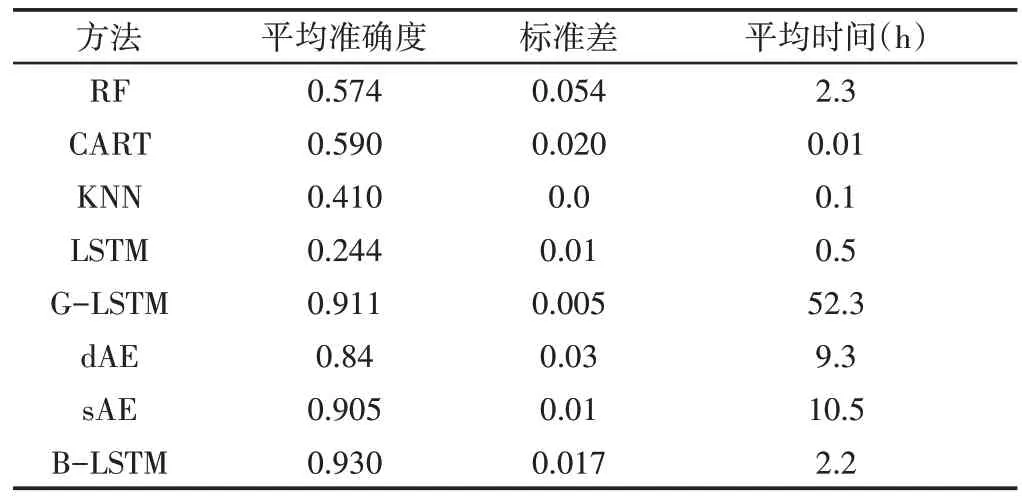
表7 提出的方法与其他方法的比较Tab.7 Comparison of the Proposed Method with Other Methods

最后一列显示了使用每种方法获得优化模型所需的平均训练时间，如表7所示。由于在这里的假设下，该模型不需要超参数优化，因此CART的时间成本较低。其次，KNN只需要优化一个超参数。实际上，前面的方法比我们的方法计算开销小，但代价是性能下降。虽然传统LSTM的体系结构可以减少LSTM的训练时间，但是没有对压缩机的故障诊断进行超参数优化。如果将此结果与类似条件下的B-LSTM迭代时间（在B-LSTM方法中训练LSTM的时间为2.2/20=0.11h）进行比较，则表明模型复杂性是由B-LSTM引起的。LSTM（1000个输入神经元）中的输入配置可延长训练时间至0.5h。提出的预处理阶段旨在减少所需的计算能力，而不损失性能。相对于网格搜索（用于G-LSTM、DAE和SAE），由于使用了贝叶斯优化，这里提出的方法具有更好的准确性和更少的训练时间。

6 结论

由于往复式压缩机的故障诊断需要复杂而耗时的特征提取过程，并且对超参数优化存在局限性，提出了一种基于深度学习和贝叶斯优化的压缩机故障诊断方法。实验结果表明：（1）在诊断任务中使用LSTM 模型和振动信号的低分辨率表示能够有效捕捉时间相关信息。（2）一些超参数空间在其接近最优区域时具有相似的性能，与预处理参数无关。在贝叶斯优化阶段，LSTM模型在有限数量的迭代中的快速收敛不是评判测试集中最佳模型的依据。（3）提出的方法在故障诊断任务中具有更好的准确性以及更少的训练时间。