压电陶瓷驱动器的复合控制方法研究
李自成,熊 轩,王后能,熊 涛
(武汉工程大学电气信息学院,湖北 武汉 430205)
1 引言
由于具有响应快、定位精度高、分辨率高等优势,压电陶瓷驱动器[1]被广泛应用在微型机械制造、超精密加工、半导体技术、显微镜技术等领域。然而由于其输入电压同输出位移之间存在严重的迟滞非线性,影响了运动控制精度和系统的稳定性。
为了减少迟滞非线性对高精度定位[2]系统的影响,实现对系统的精确控制,需要建立迟滞非线性的数学模型并加以控制。目前迟滞模型主要分为两大类:一类是基于物理机制的模型,通过对迟滞材料的微观机理深入理解的基础上给出相应的表达式来描述迟滞特性,存在着很大局限性,所建立迟滞模型往往只适用于某种迟滞材料,不利于推广;另一类是基于现象的模型,不需要考虑复杂的物理成因,模型结构简单,易于实现,以Preisach 模型、Krasnoselskii-Pokrovskii(KP)模型、Prandtl-Ishilinskii(PI)模型[3-4]等为代表,因此成为迟滞非线性建模研究的重点。针对压电陶瓷驱动器迟滞非线性的控制方案,主要分为两种:逆模型补偿[5]和闭环控制[6]。逆模型补偿方法属于开环控制,通过对迟滞特性建立逆模型,串联在系统前进行补偿,具有系统简单,响应快的特点,然而,该方法容易受到扰动影响,控制精度取决于模型精度,无法进行实时补偿。第二种是闭环控制方法,主要包括PID 控制、滑模控制、鲁棒控制[7]和自适应控制[8]等方法。此类方法将迟滞看作扰动,直接通过系统的输入、输出及误差进行补偿控制,不需要建立迟滞模型,控制精度高,系统稳定。文献[9]采用前馈结合鲁棒控制,对智能微定位系统进行补偿,有效提高了跟踪精度。文献[10]针对压电驱动定位系统的精密运动控制,设计一种数字积分终端滑模预测控制方案,实验证明具有良好的鲁棒性。然而此类方法控制器设计较复杂,加大控制器的负担,不易实现。
这里选用PI逆模型作为前馈控制器,并与滑模控制相结合构成复合控制器对压电陶瓷进行迟滞补偿控制。首先采用非等间隔阈值法建立压电陶瓷平台PI迟滞模型,利用差分进化算法对其系统辨识,求出逆模型进行前馈控制。由于前馈控制没有反馈项,不能进行实时反馈,故设计滑模控制器结合逆模型前馈控制器构成闭环控制,最后与逆模型结合PID 控制的复合控制相比,这里提出的复合控制方法精度更高。
2 PI迟滞模型
PI模型主要是用来描述弹塑性变性的一类模型。它主要是利用若干个不同阈值的Play算子或者Stop算子进行加权叠加来表达迟滞性,其表达式为:
式中:T—采样周期,t∈[t0,tN],t0≤⋅⋅⋅≤ti≤t≤⋅⋅⋅≤tN,y0—系统初始状态;y(t)—算子输出;r—算子阈值。
式(1)的初始条件为:
式中:x(t0)、y(t0)—算子初值,一般取为0。
多个阈值不同的Play 算子进行加权叠加后即可得到PI 模型,其表达式为:
对于式(3),确定ωi、ri值后就可得到PI模型。
3 参数辨识与逆模型前馈控制器
3.1 优化差分进化算法
通常情况下PI模型参数采用最小二乘法或者梯度下降法辨识,这里采取一种自适应差分进化算法进行参数识别。差分进化算法主要分为四大步骤:种群初始化、变异、交叉和选择。
3.1.1 种群初始化
首先给定个体的维数D,个体数NP,种群的迭代代数G以及个体的上下限[Xmax,Xmin]。
3.1.2 变异
进行变异操作开始迭代:对于第G代的第i个个体,即目标个体Xi,G,通过随机选取第G代种群中除第i个个体外的三个不同个体,生成新的变异个体。
通常的变异策略为:
式中:F—缩放因子,F∈[0,2];ri—当前时刻随机挑选的彼此不同的个体,r1,r2,r3∈[0,⋅⋅⋅i-1,i,i+1 ⋅⋅⋅NP]。
3.1.3 交叉
对于目标个体Xi,G和变异个体Vi,G+1进行交叉得到交叉个体Ui,G+1。给定交叉概率CR∈[0,1]。
这里随机取一个固定的Irand∈[0,...,D],是为了使至少有一堆数据与目标个体Xi,G不同。
3.1.4 选择
生成第G+1代的总群个体。根据贪婪策略,在目标个体Xi,G和上一步得到的Ui,G+1中根据评估函数选择效果更好的一个作为第G+1代种群的个体Xi,G+1。
3.1.5 变异算子优化策略
变异因子和交叉因子的策略选择是影响差分进化算法性能高低的关键因素,经典差分进化算法在搜索过程中变异算子取实常数,容易造成结果局部最优或者搜索时间过长导致的效率低下。这里采用一种具有自适应变异算子的差分进化算法,变异算子策略如下:
式中:F0—变异算子;
Gm—最大进化代数;
G—当前进化代数。
在算法初期变异率为F=2·F0,较大的变异率保证了总群的多样性;随着算法不断迭代选择最优解,变异算子逐渐接近于F0,保证全局搜索能力的同时也提高了后期局部搜索的能力。
3.2 逆模型前馈控制器
建立逆模型是前馈控制的关键因素,逆模型的准确性决定前馈控制性能的好坏,理论上逆模型可以较好补偿迟滞对系统输入信号跟踪的影响。逆模型前馈控制,如图1所示。
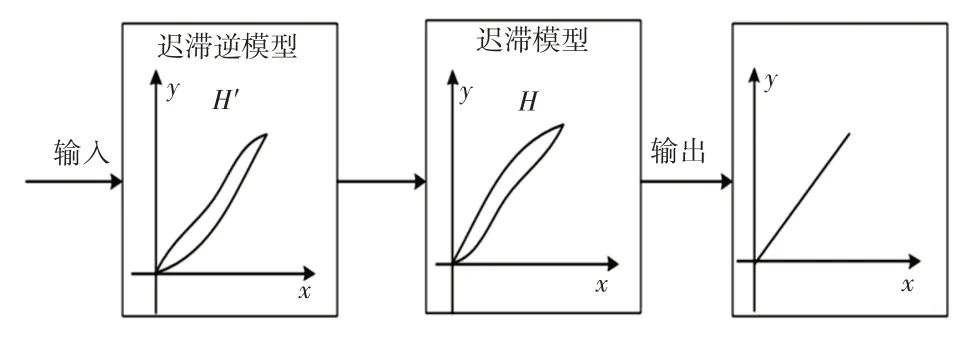
图1 逆模型前馈控制Fig.1 Inverse Model Feedforward Control
PI模型具有解析逆的特点,因此PI逆模型表示为:
其中:
目前关于PI模型阈值取值方式大多采用等间隔法,在保证模型精度的情况下,会使算子数目过多。根据文献[2],采用非等间隔阈值法,即后半段算子数目比前半段多,保证模型精度的同时也提高模型的运算速度。
这里的阈值选择如下:
通过前面的辨识方法得出来的参数带入式(8)、式(9)可得到逆模型参数,则逆模型控制器也可建立。
以频率为4Hz、幅值逐渐衰减的正弦波作为期望位移进行控制实验,PI模型采用9个Play算子叠加而成,阈值采用非等间隔法。辨识出来的PI模型参数,如表1所示。逆模型前馈输出和驱动器期望位移,如图2所示。
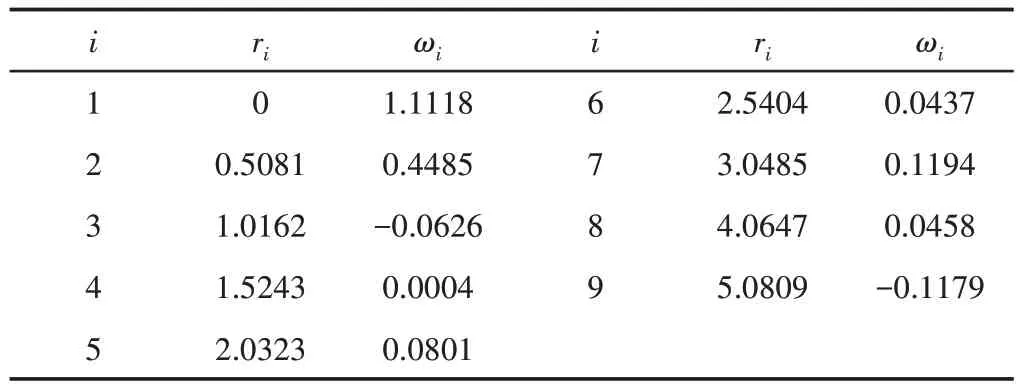
表1 PI模型参数Tab.1 PI Model Parameters
由图2可知,逆模型前馈控制平均误差为0.1574μm,均方根误差为0.1910μm,前馈控制有较好的跟踪目标位移能力。
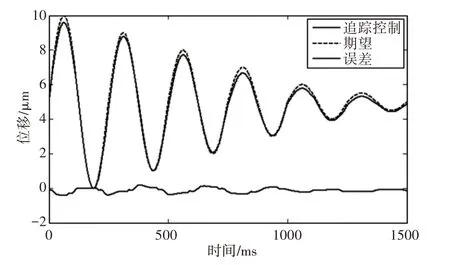
图2 逆模型前馈控制位移及误差波形图Fig.2 Inverse Model Feedforward Control Displacement and Error Waveform
4 压电陶瓷复合控制器设计
针对逆模型补偿控制没有反馈环节,无法根据输入信号的变化和外界扰动做出补偿,这里提出一种基于逆模型补偿控制与滑模变结构控制相结合的复合控制方法。其中,系统的误差e由期望信号与实际输出信号做差得到,作为滑模控制器的输入,前馈控制器的输出电压uf与滑模控制器的输出电压usmc共同组成被控对象的控制电压u,逆模型结合滑模控制系统框图,如图3所示。
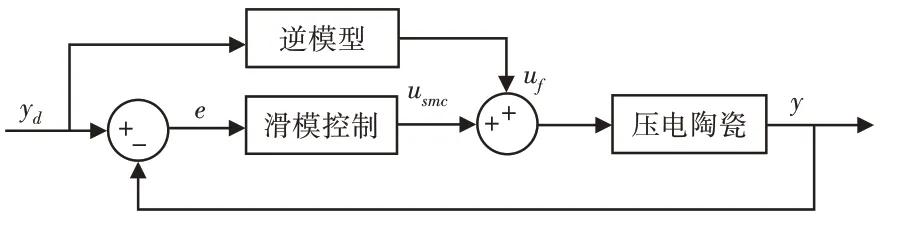
图3 逆模型结合滑模控制系统框图Fig.3 Block Diagram of Inverse Model Combined with Sliding Mode Control System
4.1 滑模控制器设计
多数情况下,压电陶瓷驱动器输入信号的频率在100Hz内,所以压电陶瓷驱动器在低频段工作区间的传递函数可以简化为一阶惯性系统,也能很好的表征压电微动平台的实际响应。
式中:m、b—系统参数;
d—控制增益;
Δ—外界扰动,假设Δ有界,|Δ| ≤D,D>0为扰动上界。
定义系统误差为:
定义滑模函数为:
其中,C>0,满足Hurwitz条件。
则有:
将式(11)带入式(14)得:
采用指数趋近律有:
结合式(15)和式(16)得滑模控制率为:
4.2 稳定性分析
定义Lyapunov函数为;
从而有:
将式(17)带入式(18)则有:
综上所述,系统达到全局稳定。
5 实验结果及分析
实验设备,如图4所示。利用德国PI公司生产的P563.3CD型压电陶瓷驱动器PEA在压电放大器E-725上进行实验。压电放大器由DSP、电压放大器及18位A/D和24位D/A转换器组成,PEA内置电容式位移传感器,采样频率为20kHz,用来测量输出位移。

图4 实验设备Fig.4 Experimental Equipment
系统参数为m=1,b=0.2,d=20。为验证控制器的有效性,采用前馈结合PID控制的复合控制方法与这里提出的前馈结合滑模控制方法进行对比。两种符合控制方法均以频率为4Hz、幅值递减三角波作为输入,所得到的跟踪波形对比图和误差对比图,如图5、图6所示。
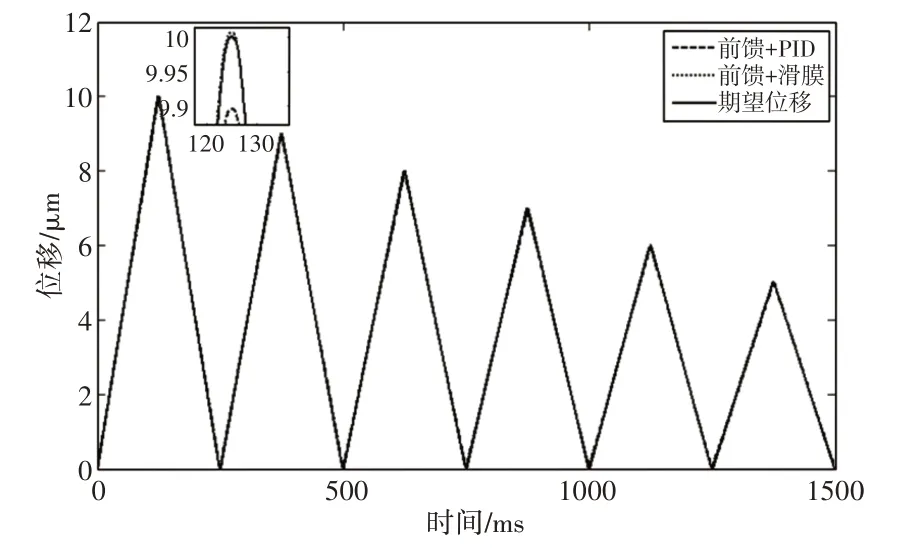
图5 两种复合控制方法跟踪波形对比图Fig.5 Comparison of Tracking Waveforms of Two Composite Control Methods
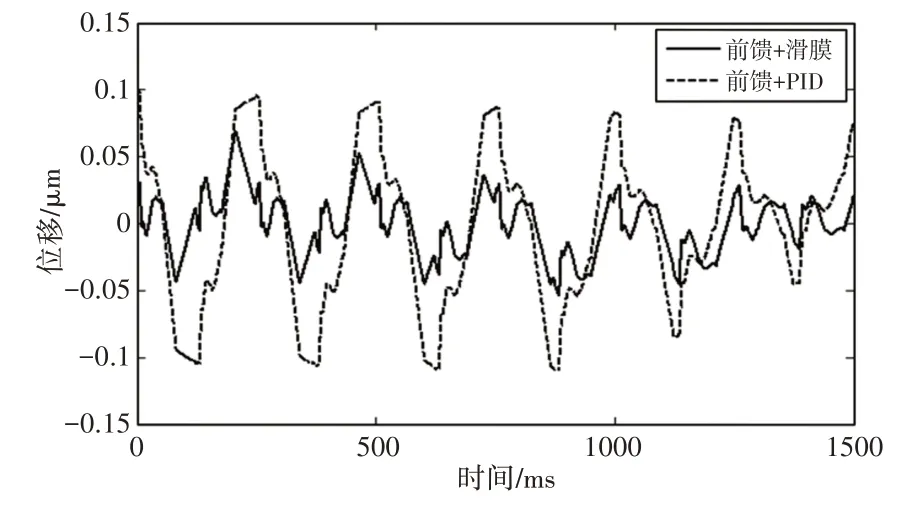
图6 两种复合控制方法跟踪误差对比图Fig.6 Comparison of Tracking Errors Between Two Composite Control Methods
由图5、图6可知,在正弦波输入下,采用这里提出的前馈结合滑模的复合控制方法的平均误差和均方根误差分别为0.018μm 和0.0226μm,而前馈结合PID 的复合控制方法的平均误差和均方根误差分别为0.0480μm 和0.0572μm,两者方法相比较,这里提出的方法比前馈结合PID 的复合控制方法的平均误差减小了0.0300μm,均方根误差减小了0.0346μm。实验结果表明,前馈结合滑模的复合控制方法精度更高,定位效果更好。
6 结束语
这里采用非等间隔阈值法,建立PI迟滞模型,利用自适应差分进化算法进行模型参数辨识并且求出逆模型,在此基础上设计了逆模型前馈控制结合滑模控制的复合控制控制器。实验结果表明,与前馈结合PID的复合控制相比,前馈结合滑模的复合控制平均误差下降了62.5%,均方根误差下降了60.4%。由此可见这里所提出的控制方法有效,具有更好的系统跟踪性能。

