基于生成对抗网络的图像超分辨率重建

王宥翔

(郑州中粮科研设计院 电气所,河南 郑州 450000)

0 引言

超分辨率(Super Resolution)通过硬件或软件提高原有图像的分辨率。图像超分辨率研究大体分为3类:基于插值、基于重建、基于学习;在技术层面则分为超分辨率复原和超分辨率重建。超分辨率重建是通过一系列低分辨率的图像生成一幅高分辨率的图像过程。

超分辨率重建是用时间带宽换取空间分辨率,实现时间分辨率转换为空间分辨率。超分辨率重建各种算法的区别主要在于网络构建的思路不同,而相同思路建构的网络也存在细微的差别。超分辨率重建大部分使用单纯的卷积神经网络(Convolutional Neural Networks,CNN)完成任务,但是CNN网络在池化层和平移不变性方面容易出现问题,文献[1]揭示并分析了卷积神经网络在变换两种空间表征(笛卡尔空间坐标和像素空间坐标)时的常见缺陷。本文基于深度学习的方案,选择更为优秀的生成对抗网络(Generative Adversarial Networks,GAN)进行超分辨率重建。

1 算法构架分析

生成模型泛指在给定一些隐含参数的条件下随机生成观测数据的模型,主要分为两类:一是建立有确切数据的分布函数模型;二是在无需完全明确数据分布函数模型的条件下直接生成一个新样本[2],如GAN(图1)。GAN通过对抗的方式,同时训练生成器(generator)和判别器(discriminator),生成器用于生成假样本,让这个假样本无限逼近真实样本,判别器则需要尽量准确地判断输入的是真实样本还是由生成器自己生成的假样本。

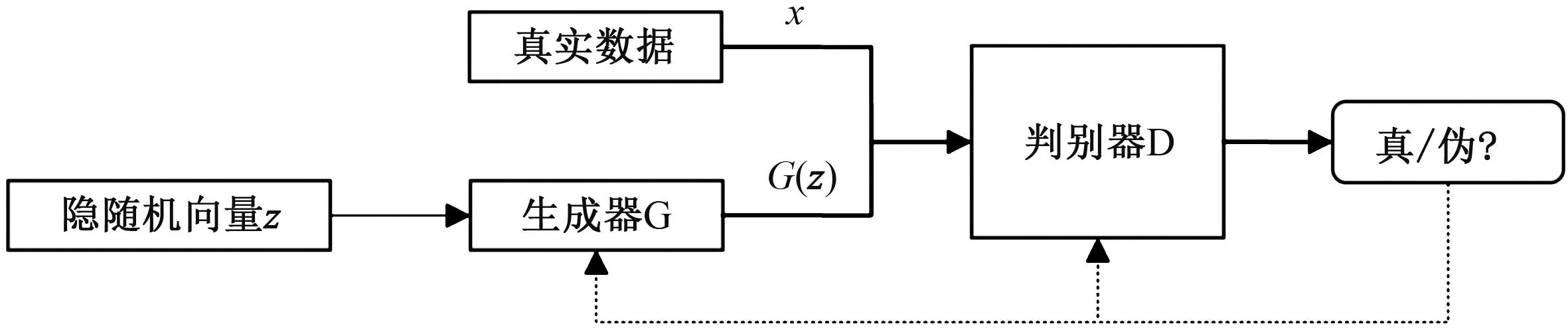
图1 GAN结构

2 具体设计

2.1 设计目标

GAN的主要结构由一个生成模型G(generator)和一个判别模型D(discriminator)组成。输入图片之后,程序提取输入的图片,并采样转化成数据tensor,数据输入到网络中开始计算,然后生成器G和判别器D开始它们的零和最大最小博弈。简单来说,通过生成器,低分辨率的图像可以重建一张高分辨率的图像,然后由判别器网络判断。当生成器网络的生成图能够很好地“骗”过判别器网络,使判别器认为这个生成图是原数据集中的图像,这里超分辨率重构的网络的目标就达成了。生成器与判别器的工作原理如图2所示,数据传递如图3所示。

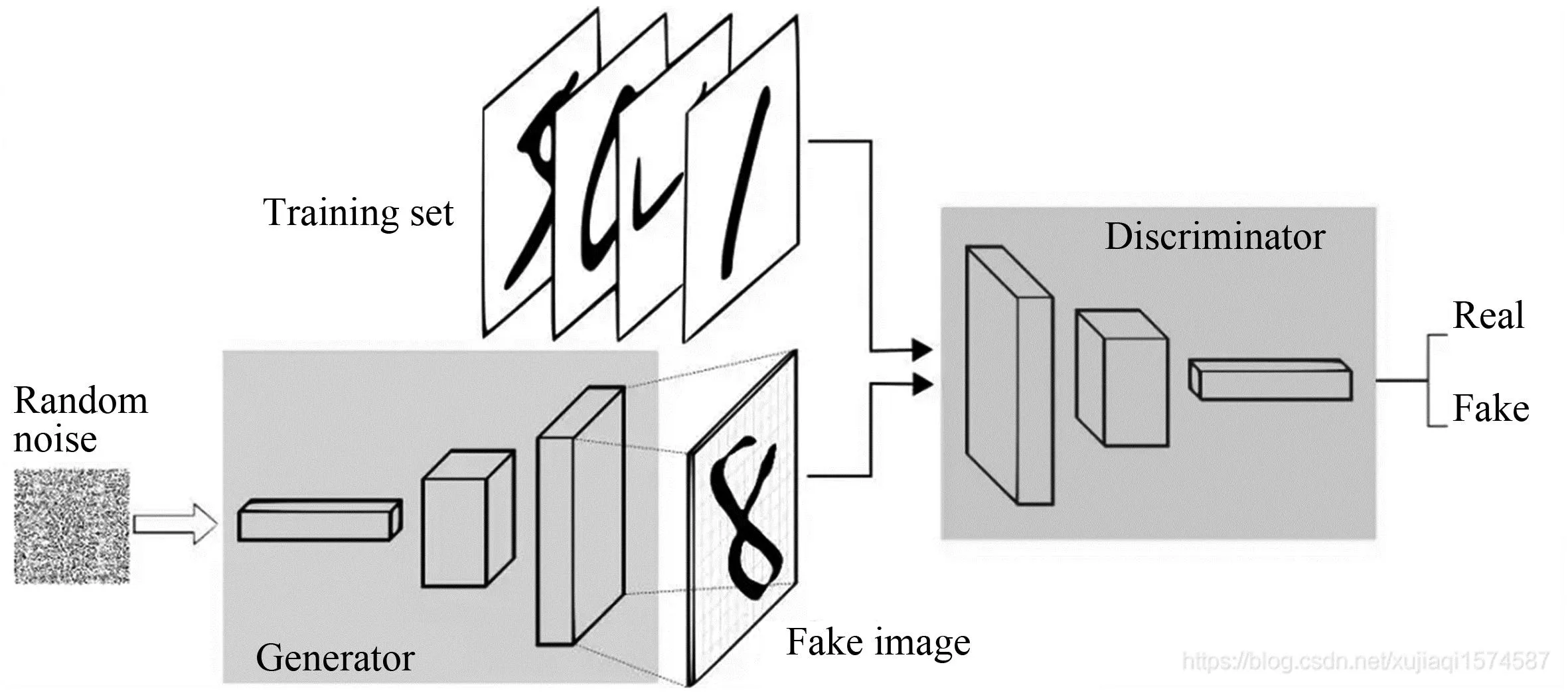
图2 生成器与判别器的工作原理

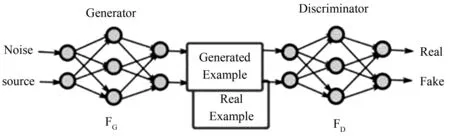
图3 生成器与判别器的数据传递

总体来说,在GAN中二者互相博弈,生成器不断生成并输出假的数据,并与训练集一同输入判别器中进行判断,继续优化学习。在这个过程中,生成器和判别器反复博弈,共同进化,最终达到超进化,经过有限次迭代之后输出数据并转化为新的图像输出[3]。图4是SRGAN的网络结构,比较直观的描述了GAN在解决图像超分辨率的网络运行思路。

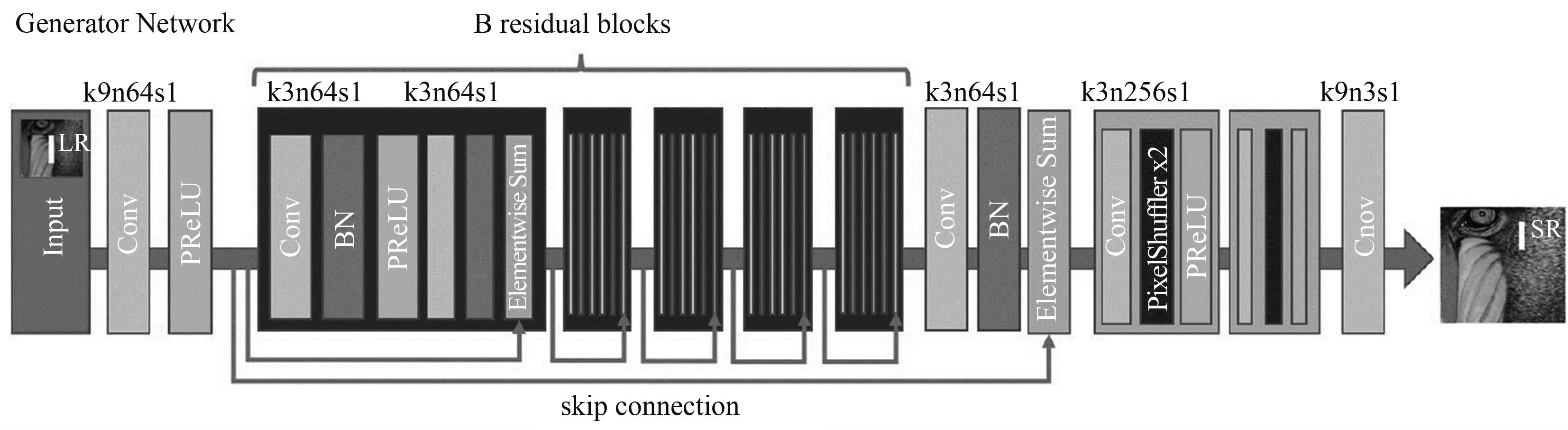
图4 SRGAN的网络结构

2.2 GAN模型

GAN模型本质上是一个最大最小博弈。目标函数为

minGmaxDV(G,D)=Ex～pr(x)[logD(x)]+Ez～pr(z)[log(1-D(G(z)))],

(1)

其中,E代表期望,x～pr(x)代表x服从pr(x)分布,z是随机噪声,服从z～pr(z)的分布。而如何得出这个结论,就要关系到生成器和判别器的网络原理。

2.2.1 判别器

判别器是程序需要优先训练的模型,使它能够判别一个输入数据是否真的来自真实数据集,如果返回值大于0.5就为真,小于0.5则为假。可以看出,使用最简单的二分类就可实现,这里使用交叉熵的方法[4]。

给定一个样本(x,y),y∈{1,0},表示其来自生成器还是真实数据。对于输入的x,判别器会返回一个y,y表示x属于真实数据的概率,

P(y=1|x)=D(x),

(2)

反之,x属于生成的图像数据概率

P(y=0|x)=1-D(x)。

(3)

判别器的目的是最小化交叉熵,交叉熵的表达式是[5]

minD(-Ex～p(x)(ylogP(y=1|x))+(1-y)logP(y=0|x)),

(4)

带入式(2)和式(3),得到

minD(-Ex～p(x)(yD(x)+(1-y)(1-D(x))))。

(5)

假设整个样本数据里面真实图像数据和生成器生成的图像数据是等比例的,

(6)

得到

(7)

然后最小化最大化互换,同时把负号变为正号,

maxDEx～pr(x)(D(x))+Ex～pg(x)(1-D(x))。

(8)

如果x～pg(x),代表x是生成器生成的,而生成器又是满足z～p(z)分布而生成的,再次替换可得

maxDEx～pr(x)(D(x))+Ez～p(z)(1-D(G(z))),

(9)

即所需求的目标函数。

2.2.2 生成器

生成器是判别器训练完成后才开始训练的模型,作用是在给定输入的情况下得到一定的输出,然后继续送给判别器判断,之后返回给自身一个误差值,从而继续学习。

生成器的目标刚好和判别器相反,即让判别器把自己生成的样本判别为真实样本。因为GAN网络的本质数学模型是一个最大最小博弈,通过判别器得到了目标函数,从而得到最大值max,所以生成器的目的就是得到最小值min[6]。目标函数

maxDEx～pr(x)(D(x))+Ez～p(z)(1-D(G(z)))

(10)

由两部分构成,由后一部分可得生成器目标

minGEz～p(z)(1-D(G(z)))。

(11)

将生成器与判别器的函数结合,即得到生成对抗网络的模型,

minGmaxDV(G,D)=Ex～pr(x)(logD(x))+Ez～p(z)(log(1-D(G(z))))。

(12)

2.3 GAN的原始损失函数

训练时的优化需要引入生成对抗网络的损失函数,

LossG=log(1-D(G(z)))or-log(D(G(z))),LossD=-log(D(x))or-log(1-D(G(z))),

(13)

LossG=log(1-D(G(z)))or-log(D(G(z)))。

(14)

由生成器的目标式得

minGEz～p(z)(1-D(G(z)))。

(15)

后面一部分是原作者Ian Goodfellow提出的,效果等同于优化前面那个而且梯度性质更好。

LossD=-log(D(x))-log(1-D(G(z))),

(16)

maxDEx～pr(x)(D(x))+Ez～p(z)(1-D(G(z)))。

(17)

2.4 GAN网络的问题

2.4.1 判别器越好,生成器梯度消失越严重

在最优判别器的条件下,最小化生成器的损失函数和最小化P1与P2之间的JS散度是等价的[7],

(18)

对于P1与P2来说是完全对称的,JS是两个KL散度的叠加(KL散度又称相对熵),一定是大于等于0的,所以JS散度一定大于等于0。在这里可能会出现严重的问题:如果两个分布没有重叠的话,JS散度就为0,而在训练初期,两个分布必然是基本不会重叠,所以假如在这里判别器被训练得过于好,损失函数就会经常收敛到固定的-2 log 2,从而产生没有梯度的情况。然后网络就没法继续训练下去了,对抗网络中的生成器和判别器是要一起进化变强的,一个过于强将会导致另一个无法继续训练[8]。

2.4.2 可能出现梯度不稳定和模式崩溃

GAN采用的是对抗训练的方式,判别器的梯度更新来自判别器,生成一个样本,交给判别器去评判,判别器会输出生成的假样本是真样本的概率。生成器会根据这个反馈不断改善。但假如有一次生成器生成的并不真实,判别器却出了问题,给了正确评价,或者在一次生成器生成的结果中存在某一些特征被判别器所认可了,这时候生成器就会认为这里的输出反而是正确的,接下来继续输出相同的数据判别器就还会给出高的评分,最终就会导致生成结果中的一些重要信息或特征残缺[9]。

3 网络构建

3.1 整体搭建网络思路

首先需要生成器(G)生成图片模型,判别器(D)判断图片是否为真,如图5所示。

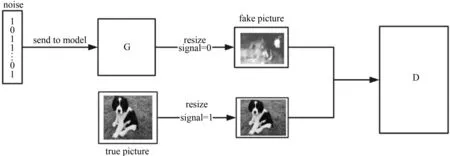
图5 GAN网络架构

首先需要向生成器输入一个噪声,生成随机数组,继续输出一个数据转换为一张图片,输入图片之后,经过判别器来输出是一个数1或者0,代表图片是否是狗。

然后通过训练网络,把真图与假图拼接,打上不同的标签,真图为1,假图为0,送到网络中训练。

3.2 训练网络构造

3.2.1 数据输入

声明集合dataloader,将训练和测试数据都放入其中。

3.2.2 训练网络

先重写构造函数,构造一个父类的函数 “super”,然后定义网络结构block,运用nn.sequential将多个函数,如卷积函数Conv2d和激活函数PReLU,并列放置,经过多个ResidualBlock残差网络模块处理。采样之后,进入前向传播forward函数,最后经过tanh函数映射到-1到1,最后得到一个0到1的数据输出[10]。

判别器是一个二分类的模型,先重写构造函数构造父类函数,然后进入多层的网络,在进入一层池化层之后,取平均值下采样,得到1×1的数据,最后只得到batchsize的数据,然后通过sigmoid函数将实数域映射到0～1,即batchsize的概率,符合判别器二分类概率的原理[11]。

4 优化整体训练

通过优化器进行判别器的训练。首先为了优化判别器,将其梯度归零,然后规定判断真实图片和虚假图片的概率,接着规定判别器的损失函数,计算出d_loss,然后执行上面的步骤。

训练生成器时,将生成器的梯度置零后,生成一个假的图片,输入判别器,得出判别器判断为假的概率,输入给生成器的损失函数,计算得出g_loss,再反向传播backward,最终运行开始训练。

完整的网络架构中日志记录以及数据输入输出可视化不再赘述,可将生成模型记录保存在字典文件pth之中,以供之后的测试或者训练使用。

5 训练结果与测试结果

完成了GAN构造并经过训练之后,进行网络性能测试。笔者下载了超分辨率重构的数据集,包含×4和×8的每个大约3 000张图片的测试用数据集,数据集文件列表如图6所示。

图6 超分辨率重构数据集

因为神经网络训练运算量巨大,且需要占用大量内存,所以这里将其放到训练试验机上,运用4块RTX 3090显卡进行训练。训练整体大概1 000个迭代epoch,最终得到两个记录模型权重的pth文件,这两个权重文件可以直接输入测试网络,以下通过几个测试图片检测训练的结果。

测试所用的一组原图Ground truth,如图7所示。×4超分的测试结果如图8所示。×8超分的测试结果如图9所示。可以看出,在×8的超分上,如果细节比较小的话,得出的超分图会比较边缘性的模糊,×4的超分结果已经比较理想。

图7 原图

图8 ×4测试结果

图9 ×8测试结果

整体来说,网络训练结果比较理想,成功收敛且没有出现梯度消失以及模式崩溃的情况。说明利用深度学习的神经网络中的GAN生成对抗网络,能够实现图像超分辨率的目标。