融合注意力机制的时间卷积知识追踪模型

邵小萌，张 猛

（华中师范大学 计算机学院，武汉 430079）

0 引言

在线教学平台提供了高质量的课程资源和便捷的学习方式，吸引了大量用户使用。如何利用人工智能技术对这些平台上的海量学习数据进行分析，为用户提供个性化教学，成为教育数据挖掘领域的重要研究课题。知识追踪可以从在线平台上的交互数据中自动挖掘学生随时间变化的知识状态，预测学生未来的学习表现，从而为学生提供精准的个性化教育。

知识追踪根据学生的交互记录预测学生未来的表现，是一种时间序列建模任务。深度知识追踪（Deep Knowledge Tracing，DKT）［1］是目前最流行的模型之一，该模型利用循环神经网络（Recurrent Neural Network，RNN）对学生的交互记录建模。虽然DKT 的预测效果相比传统模型有很大提升，但是将RNN 的隐藏状态解释为学生的知识状态过于抽象，导致DKT 的可解释性不足［2］；并且在许多实际应用中，RNN对于较长序列容易出现梯度消失问题，无法利用很久以前的输入信息，这使得DKT 在处理学生的长时间学习记录时也会存在类似缺点［3］。

近年来，一些研究表明特定结构的卷积神经网络可以很好地应用于时间序列建模问题，并在预测精度和计算复杂性方面优于RNN，如时间卷积网络（Temporal Convolutional Network，TCN）。Li 等［4］利用TCN 能够建立更深层的神经网络的优点，挖掘更抽象的语义特征，对视频各帧的目标进行分割定位和动作识别；You 等［5］利用TCN 运算效率高的特点，建立了能够处理大规模数据的广告推荐系统。本文尝试使用时间卷积网络对学生的历史交互记录建模，并融入注意力机制，构建了一种新的知识追踪模型。

本文提出一种融合注意力机制的时间卷积知识追踪（Temporal Convolutional Knowledge Tracing with Attention mechanism，ATCKT）模型。

本文的主要工作如下：

1）使用时间卷积网络提取学生动态变化的知识状态，时间卷积使用扩张卷积和深层网络结构，可以学习到长时间的交互信息，减少信息遗漏。

2）考虑到学生对于相似的题目容易做出相同的答题结果，使用基于题目的注意力机制学习特定权重矩阵，计算学生的历史相关表现，提升了模型的可解释性。

3）在ASSISTments2009、ASSISTments2015、Statics2011 和Synthetic-5 这4 个公开数据集上将新提出的ATCKT 模型与四种具有代表性的知识追踪模型进行对比实验，实验结果验证了本文模型在预测准确率和运算效率方面的提升效果。

1 相关工作

知识追踪可以根据已有的交互记录预测学生未来的表现，图1 描述了一个基础的知识追踪任务。已知3 个学生S1、S2、S3分别回答了与2 个不同知识点k1、k2相关的6 道题目e1～e6，知识追踪可以根据前6 道题目的答题结果，预测学生下一个时刻正确回答题目e7的概率。

图1 知识追踪示例Fig.1 Example of knowledge tracing

知识追踪方法主要分为三种：第一种是基于概率图模型的知识追踪，如贝叶斯知识追踪（Bayesian Knowledge Tracing，BKT）［6］，将学生的知识状态建模为一组二元变量，使用隐马尔可夫模型更新这组变量；但是BKT 无法捕捉不同概念间的关系，并且使用二元组来表示学生的知识状态是不合理的［7］。第二种是基于矩阵分解的知识追踪，如使用因子分解机来处理知识追踪［8］。第三种是基于神经网络的知识追踪。

Piech 等［1］在2015 年提出深度知识追踪（DKT），首次将神经网络应用于知识追踪。DKT 采用RNN 对学生的交互记录建模，将学生的交互记录转化成独热编码作为输入，使用RNN 的隐藏状态ht表示学生的知识状态。与BKT 相比，DKT能够挖掘题目间的隐藏关系，准确率得到大幅提升，但仍存在可解释性不足和长序列依赖等问题，且DKT 将交互记录以独热编码的形式作为输入，缺乏学习特征，不利于模型提取学生的知识状态。

许多研究人员在DKT 的基础上进行改进，如Yeung 等［3］提出DKT+（Deep Knowledge Tracing plus），在损失函数中加入正则化项来平滑预测中的过渡，减轻DKT 对学生状态预测波动较大的问题。Minn 等［9］提 出DKT-DSC（Deep Knowledge Tracing and Dynamic Student Classification for knowledge tracing），通过对学生阶段性学习状态的聚类进行预测，但是这些变体模型依然无法摆脱RNN自身结构的缺陷。

许多学者尝试使用其他方法处理知识追踪问题。Zhang等［10］提出一种动态键值对记忆网络知识追踪模型（Dynamic Key-Value Memory Network，DKVMN），使用一个动态矩阵来存储每个知识点对应的知识状态，当学生完成练习后，更新与该题目有关的知识点的知识状态，提升了模型的可解释性；Pandey 等［11］提出SAKT（Self Attentive Knowledge Tracing）模型，完全使用Transformer 模型［12］处理知识追踪，Transformer 模型基于自注意力机制，脱离了RNN 的结构限制，不存在长序列依赖问题；Nakagawa 等［13］提出GKT（Graphbased Knowledge Tracing）模型，将知识点之间的关系表示为有向图，将知识追踪任务转化成图神经网络中的时间序列节点级分类问题；此外，一些工作［14-15］通过挖掘知识点和习题之间的关联，为模型赋予更多的学生和题目特征来提高模型的可解释性。

2 融合注意力机制的时间卷积知识追踪

本文提出融合注意力机制的时间卷积知识追踪ATCKT模型。如图2 所示，该模型由4 个部分组成，分别是嵌入模块、注意力模块、知识状态提取模块和预测模块。首先，通过嵌入层学习题目的嵌入向量，将题目嵌入与答题结果拼接作为学生的交互记录；然后，使用注意力机制根据题目之间的相似度，为不同题目的交互记录分配不同的权重，得到学生的历史相关表现；最后，使用时间卷积网络提取学生的知识状态特征，与题目的嵌入向量做点积运算，经过sigmoid 激活函数得到学生正确回答下一道题目的概率。

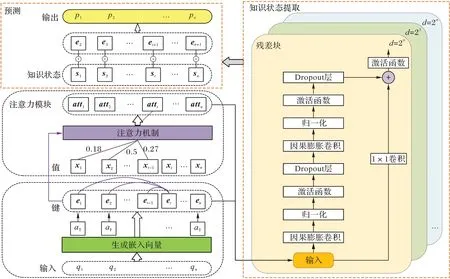
图2 ATCKT模型结构Fig.2 Structure of ATCKT model

2.1 交互序列嵌入

学生的历史交互记录被表示为题目的嵌入向量与答题结果的拼接。给定一个学生i的N条交互序列Xi={xi1，xi2，…，xin}，其中xit=(qit，ait)，t∈(1，N)，qit表示该学生在t时刻回答的题目，ait为1 或0，表示该题答对或答错。假设数据集包含M道不同的题目，随机初始化嵌入矩阵E∈RM×K，矩阵的每一行et∈RK为题目qt的嵌入向量，K表示题目的嵌入向量维度，在模型训练过程中et可以自动学习到题目有意义的表示，隐式地包含了题目涉及的知识点、题目难度等信息。规定aT=(1，1，…，1)和aF=(0，0，…，0)是两个与et维度相同的全1 和全0 向量。将xt表示为et和aT或aF的连接，得到学生的历史交互记录xt∈R1×2K，如式（1）所示，⊕表示连接两个向量：

2.2 注意力模块

在实际场景中，如果一些题目涉及相同的知识点，或难易度相似，则学生对这些题目可能会做出相同的答题结果；并且，学生的历史答题表现在一定程度上反映了学生对不同知识的掌握情况。基于此，本文使用基于题目的注意力机制，根据题目间的相似程度，量化不同题目的历史交互记录对学生知识状态的贡献度，具体反映学生对不同知识点的掌握情况。本文将当前时刻回答的题目et作为注意力机制的查询query，学生前t个时刻作答的题目e1～et-1及对应的交互记录x1～xt-1作为键-值对，如式（2）～（4）：

其中：Wquery∈RK×K、Wkey∈RK×K，用来对et和ei行线性变换，K为题目的嵌入向量维度。然后对query 和key 进行点积运算，使用softmax 激活函数进行归一化得到注意力权重αi，如式（5）和（6）：

2.3 知识状态提取

本文将嵌入层得到的学生交互记录和注意力模块得到的学生历史综合表现拼接输入时间卷积网络（TCN），提取学生每个时刻的知识状态。

TCN 在一维卷积的基础上，增加了因果扩张卷积。因果卷积保证模型在t时刻的输出只依赖前t时刻的输入，防止未来的信息泄露，扩张卷积［16］通过间隔一些输入来增大视野范围。图3展示了一个因果扩张卷积，其中d表示扩张系数。

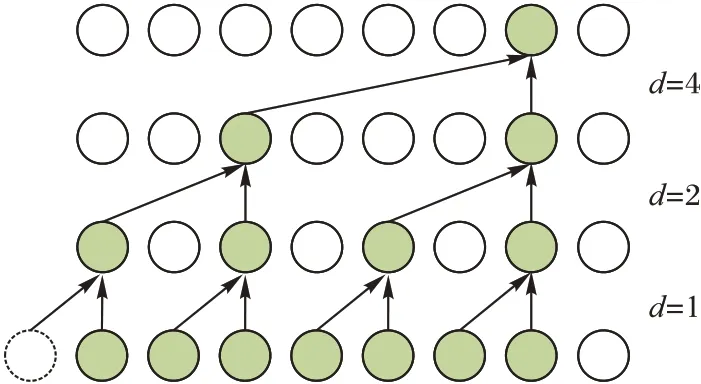
图3 因果扩张卷积Fig.3 Causal expansion convolution

由图3 可知，当神经网络层数足够多时，TCN 可以学习到所有输入数据，产生高精度的预测结果；同时为了避免深层模型中出现网络退化，TCN 在卷积层之间增加了残差连接［17］。本文模型的残差块内包含：因果扩张卷积、层归一化将该层的所有神经元归一化、ReLU（Rectified Linear Unit）激活函数和Dropout 层防止过拟合。

TCN 提取学生每个时刻的知识状态矩阵S∈RN×K，N表示学生交互记录的全部数量，st∈RK的维度等于题目的嵌入维度K，表示学生在该时刻对于知识的掌握情况。

2.4 预测与训练

将学生的知识状态st与下一时刻要回答的题目et+1进行点积操作得到yt+1，然后对yt+1使用sigmoid激活函数得到pt+1表示预测的学生正确回答下一道题目的概率，计算公式如下：

本文采用交叉熵损失函数作为真实值at与预测值pt之间的损失函数L，采用最小化L的方式优化题目的嵌入向量、网络参数和学生正确回答下一道题目的概率pt。损失函数L如式（10）所示：

3 实验与分析

为了评估本文模型的效果，在4 个常用公开数据集上进行了对比实验，并与四种具有代表性的模型进行比较，验证本文模型的准确性和高效性。

3.1 数据集

各个数据集所包含的学生数、题目数和交互记录数如表1 所示，其中Synthetic-5 是人工数据集，其余均为真实数据集。ASSISTments2009 与2015［18］分别来自在线教育平 台ASSISTments 上2009 年和2015 年的数据；Statics2011 来自《工程静力学》课程；Synthetic-5 是DKT 模型使用的数据集，它模拟了4 000 名虚拟的学生回答50 个题目。

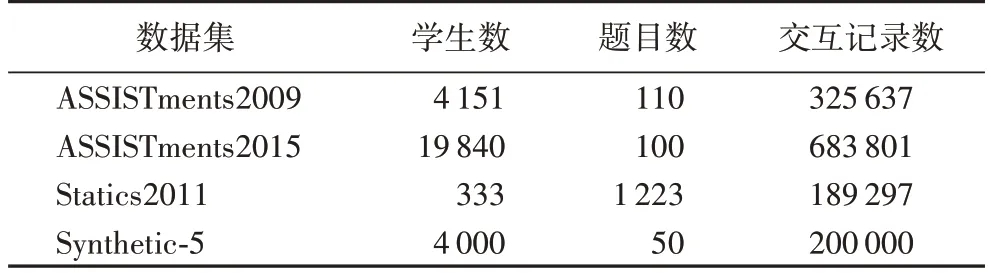
表1 数据集介绍Tab.1 Dataset introduction

3.2 对比模型

本文选取了4 个具有代表性的知识追踪模型进行了对比实验，分别是：DKT、DKVMN、卷积知识追踪（Convolutional Knowledge Tracing，CKT）［19］和SAKT，如下：

DKT：首次使用循环神经网络处理知识追踪任务，是知识追踪领域广泛使用的经典模型。

DKVMN：使用动态键值对记忆网络存储并更新学生关于每个知识概念的知识状态，增强了模型的可解释性。

CKT：在建模学生状态时考虑了学生的先验知识和学习率，丰富了学生特征。

SAKT：使用Transformer 结构处理知识追踪，脱离了RNN的结构限制，不存在长序列依赖问题。

3.3 实验设置

在数据预处理中，删除了少于3 条答题记录的学生数据，并对拥有超过380 条答题记录的学生数据做截断处理，将超过380 条的部分作为一位新的学生数据。

本文模型的参数设置为：模型训练的学习率为2E-3，epoch 为32；式（1）中题目嵌入的维度为10；TCN 中卷积核大小为6，共12 个残差块，扩张卷积的扩张系数d=2n，每隔一个残差块增大一倍，n初始值为0。残差模块中Dropout 比率初始值设置为0.05。

3.4 结果分析

本文使用曲线下面积（Area Under the Curve，AUC）和准确率（Accuracy，Acc）指标来衡量ATCKT 模型与对比模型的预测效果，不同模型在各个数据集上的实验结果如表2所示。

表2 不同知识追踪模型的实验结果对比 单位：%Tab.2 Comparison of experimental results of different knowledge tracing models unit：%

本文提出新颖的时间卷积方式处理知识追踪问题，使用嵌入向量的形式表示题目，增强模型的特征提取能力，使用时间卷积网络提取学生的知识状态，并融合基于题目的注意力机制判断历史交互对未来答题的影响。表2 的实验结果显示，与其他模型相比，ATCKT 模型的AUC 和Acc 值在4 个数据集上是最高的，特别在ASSISTments2015 数据集上提升最多，AUC 值相比DKT 提升了接近20 个百分点，达到92.22%。ACC 值相比DKT 提升了接近11 个百分点，达到86.11%。

3.5 时间卷积的有效性验证

为了验证时间卷积对长序列特征提取的有效性，本文使用TCKT-One-Hot 与DKT 进行了单一变量对比实验，TCKTOne-Hot 与DKT 采用相同的独热编码形式作为输入，使用时间卷积网络对学生的历史交互进行建模，没有融入注意力机制。两种模型的预测结果如表3 所示。

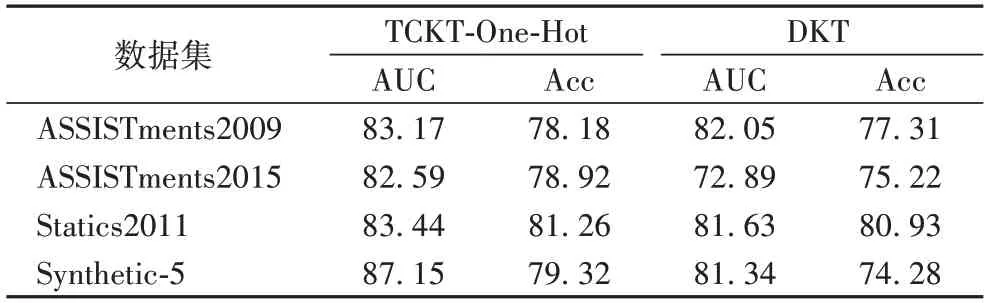
表3 TCKT-One-Hot与DKT模型的预测结果 单位：%Tab.3 Prediction results of TCKT-One-Hot and DKT models unit：%

由表3 可得，在4 个数据集上，TCKT-One-Hot 的AUC 值和Acc 值比DKT 均有明显提升，特别在ASSISTments2015 数据集上提升最多，AUC 值相比DKT 提升了接近10 个百分点。这表明时间卷积TCN 中的扩张卷积和深层神经网络能够有效考虑到学生更长时间的学习记录，在一定程度上减轻了RNN 的长序列依赖问题。

3.6 题目嵌入向量相似度可视化

训练完成的题目嵌入向量隐式地包含了题目难度、题目涉及的知识概念等丰富的题目特征信息，有助于神经网络进行特征提取。为了验证该结论，本文在ASSISTments2009 数据集上随机选择了7 个题目，分别是86 号、75 号、85 号、89号、99 号、77 号和22 号题目，计算它们的嵌入向量之间的余弦相似度，表4 介绍了每个题目主要涉及的知识概念，计算结果如图4 所示。方块内部的数值表示对应题目的相似度，相似度越大方块颜色越深。

表4 题目编号与其对应的知识概念Tab.4 Exercise problem numbers and corresponding knowledge concepts

由图4 可以看出，与知识点“体积”相关的86 号和75 号题目相似度较高，相似度为0.7，与知识点“线性方程”相关的89 号和99 号题目相似度较高，相似度为0.63，而其他题目之间相似度很低。实验结果表明经过训练后的题目的嵌入向量包含不同题目之间的相关性信息，提高了模型的可解释性。

图4 题目嵌入向量的余弦相似度Fig.4 Cosine similarity of embeddings of exercise problems

3.7 预测结果可视化

为了具体说明ATCKT 模型预测的准确性，本文在ASSISTments2015 数据集中随机选择了一个学生，截取其分别使用ATCKT 和DKT 模型的部分输出结果，进行可视化对比。如图5 和图6 所示，图片左侧数字59、90、16、21 和15 表示题目编号，每一列下方两个数字表示一次交互记录，表中0 到1 之间的数字表示模型预测学生下一次能够正确回答相关题目的概率。在实际情况中，若学生连续答错一道题目，表示学生对该题的掌握程度较差，未来答对该题目的概率很小。但在图中红框内，当学生连续答错90 号题目后，ATCKT模型预测的学生下一次正确回答90 号题目的概率值在0.2～0.4，而DKT 的预测值在0.5～0.6，而这明显不符合实际情况。该结果表明，ATCKT 模型中的Attention 机制能有效识别历史相关答题记录对未来知识状态的贡献度，提升了模型的可解释性和准确性。

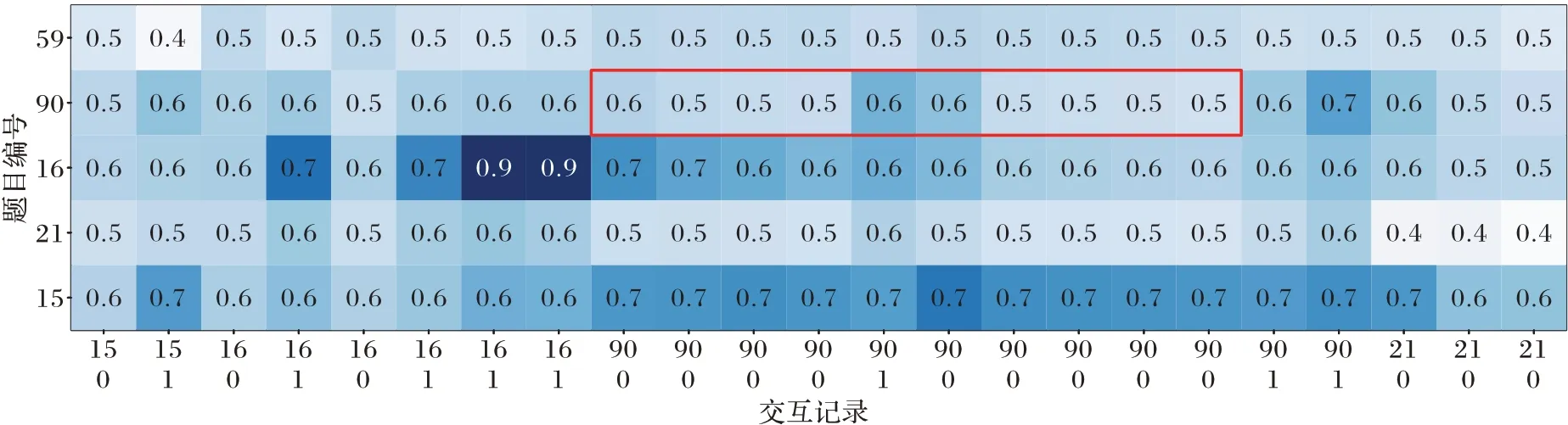
图5 DKT模型的预测结果可视化Fig.5 Visualization of prediction results of DKT model

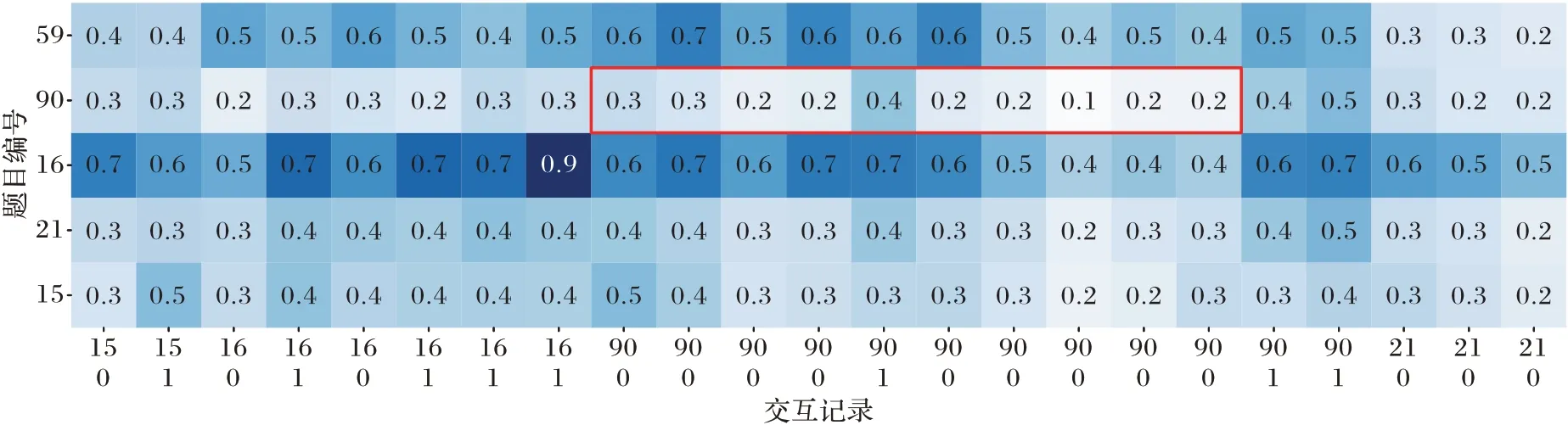
图6 ATCKT模型的预测结果可视化Fig.6 Visualization of prediction results of ATCKT model

3.8 训练时长分析

RNN 中每一时刻的输出依赖上一时刻的隐藏层状态，无法并行计算，而卷积神经网络中同一层次的计算均使用同一卷积核，不存在前后关系，可以同时进行计算，因此训练速度更快。为验证ATCKT 模型的运算效率，本文与DKT 模型进行了对比实验。本文的实验环境为Windows 10 64 位，i9 处理器，32 GB 内存，采用为Python3.6，Tensorflow 1.15 版本。ATCKT 与DKT 模型的训练时间如表5 所示，可得ATCKT 模型的训练速度明显快于DKT。

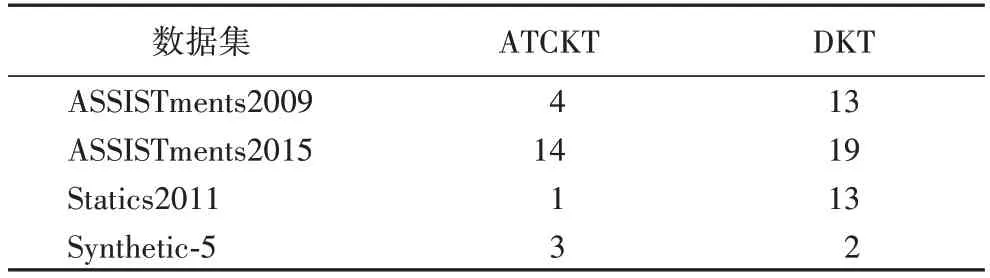
表5 ATCKT与DKT模型的训练时间对比 单位：minTab.5 Comparison of training time between ATCKT and DKT models unit：min

4 结语

针对DKT 模型的可解释性较弱和长序列依赖两个问题，本文提出一种融合注意力机制的时间卷积知识追踪ATCKT 模型，该模型根据题目之间的相似度，使用基于题目的注意力机制，识别并强化历史不同题目的交互记录对学生知识状态的贡献度，丰富学生的个性化特征，使用时间卷积提取学生的知识状态，对学生未来的答题结果进行预测，通过扩张卷积和深层神经网络，缓解DKT 的长序列依赖问题。实验结果表明本文模型在多个数据集上的准确率均优于对比模型，且运算性能小幅提升。在后续的研究工作中可以挖掘实验数据中更多的学生的个性化特征，以及题目和知识点之间的深层次的关联，进一步加强模型对学生知识状态的表征能力。