基于有限元分析的气动力射流泵数值模拟研究
郭邦瑞,胡莉莉,王 彤
(西安石油大学 机械工程学院,西安 710065)
0 引言
在对气井进行开发的过程中,井底会出现产水现象,当地层水或烃类解析液进入井筒,井中水的含量较小而天然气的速度相对较大时,水便会以液滴的形式被携带到地面,导致天然气的产出量降低,随着天然气的储量不断降低,井底压力下降,井筒中的水便无法被携带到地面,就会在井底形成积液,导致气井无法产出天然气,此时,便需要对气井采取排水采气的相关措施[1-3]。本文主要讨论射流泵排水采气工艺,传统的射流泵排水采气采用水做为动力介质,而采用天然气做为动力介质时,与液体介质所采取的管柱排列有所区别,若气体介质与液体介质采用相同的管柱排列,则气动力射流泵无法达到所设计的效率,因此需根据气体介质的管柱排列来确定气动力射流泵的相关参数[4-5]。
白雅婷等[6]通过Fluent对射流泵进行了数值模拟研究,得出了喷嘴距为d~2.0d时射流泵的效率较高,以及射流泵的性能与面积比有着很大的关系,当面积比为6.76时,射流泵的性能最佳。张天礼等[7]对酸性气田的射流泵排水采气进行了模拟研究,得出了采用二级射流泵性能可达50%,且采用二级射流泵时比一级射流泵有着更好的排水采气效果。邢晓光等[8]研究了智能分层射流泵排液技术,并进行了现场应用,发现了排液成本降低而排液效率提高了的成果。
本文针对气动力射流泵进行数值模拟研究,研究其在不同的工况参数以及不同的结构尺寸下的排水采气性能的变化规律。
1 气动力射流泵排水采气系统节点分析
节点分析主要用于分析气动力射流泵排水采气系统中的气体介质流动管柱尺寸气井产量、气体介质注入量、油管尺寸、混合气液排出管尺寸、压缩机压力等参数对整个排水采气系统的影响,优化排水采气系统参数,确定气动力射流泵气体介质入口速度及排出管速度。
在确定各个节点的参数时,需先假设气井有多个不同的产量,针对每一个产量,可根据地层气液流动状态确定井底压力,以此绘制流入曲线,再假设气井有一系列的注气量,针对每一个注气量,确定其注气点及注气深度,以此确定气井的井底流压,绘制流出曲线,将流出曲线与流入曲线互相迭加,确定两曲线交点处的压力及产量,最后可根据数值模拟所确定的工况分别获得气动力射流泵的流入压力及流出压力。通过这种方法获得的设定工况条件下的参数更加准确,可以建立出更加准确的气动力射流泵物理模型,数值模拟时所设定的边界条件也更加准确,使得模拟出的结果也更加具有可信度。图1为系统节点分析图。

图1 系统节点分析
2 计算模型分析
气动力射流泵物理模型主要包括:进气管、吸液管、喷嘴、喉管、扩散管及混合气液排出管,其总体结构如图2所示。根据研究的气井工况确定管柱的相关参数,抽取气动力射流泵所在管柱的动力介质及混合气液流动区域在Solidworks中进行建模,本文中模拟管柱的相关参数为入口管柱:外径48.3 mm、内径40.9 mm、横截面积131 3.15 mm;出口管柱:外径88.9 mm、内径76 mm、横截面积270 2.84 mm;当量出口管柱内径58.68 mm、横截面积270 3.02 mm。

图2 气动力射流泵结构图
气动力射流泵的结构参数为:喷嘴直径3 mm、喷嘴距6 mm、喉管直径3.8 mm、喉管长度48 mm、扩散管角度6.05度、扩散管长度51 mm。
压缩机将天然气压缩到一定压力后将天然气打入进气管,高压气体进入射流泵,而后经喷嘴形成高速射流,此时因高速气体射流地形成使得吸液管的压力远低于井底压力,产生抽吸的效应,使得井底积液进入吸液管,而后与告诉天然气一同进入喉管,进入喉管后两者进行混合以及能量交换,此时混合气液的速度降低压能逐步升高,随后进入扩散管进行进一步的混合以及能量交换,当压能升高到一定程度时,混合气液经排出管到达地面[9-11]。
2.1 网格划分
气液两相在气动力射流泵内部的流动状态为有限空间射流,这种流动状态比较复杂,因此在对气动力射流泵进行仿真模拟时,需对气动力射流泵的物理模型进行网格划分,通过网格划分,能够得到在设定的工况条件下的更加准确合理的流场分布。
抽取射流泵内部流场所在区域制成模型。使用Workbench Meshing对模型进行网格划分,网格结构采用三面体,为确保网格的质量需对网格的尺寸进行调整,在进行流场仿真之前对网格进行检验,检验完成之后在进行网格无关性验证,对不同尺寸的网格进行仿真模拟,当结果几乎不发生改变时,便可采用当前的网格尺寸进行仿真模拟,此时所得到的仿真结果相对准确,划分结果图如图3所示。

图3 气动力射流泵网格划分
将划分的网格模型导入Fluent中进行数值模拟,动力介质选择空气,根据工况条件计算天然气的密度,对动力介质进行相应的密度修改,吸入液选择水。为了确保射流模拟的准确性,选用Realizable k-ε湍流模型,也可以更清楚地表现出流场的细节,算法采用Simplec,根据所要研究的工况确定各边界条件[12,13]。
2.2 湍流模型
湍流是不规则、多尺度、有结构的流动,其流动状态一般是三维的、非定常的,在流动的过程中具有很强的扩散性和耗散性。从物理结构上看,湍流是带有旋转结构的涡叠合而成的流动,这些涡有着各种不同的尺度,且尺度的大小及旋转轴的方向分布是随机的。大尺度的涡会不断的从主流获得能量,小尺度的涡通过与大尺度的涡进行涡间作用来获得能量。但由于流体具有粘性,因此在流动的过程中,小尺度的涡会不断消失,这样流体的机械能就会慢慢转化为热能。在能量转化的同时,由于边界、扰动及速度梯度的作用,流体中又会不断产生新的涡,使得湍流运动得以继续存在并得到发展和延续。标准的k-ε模型作为流场计算中的主要工具,有着适用范围广、经济、合理的精度等优点。湍动能输运方程是经过精确的方程推导得到的,耗散率方程是通过物理推导,数学上模拟相似原型方程得到的[14,15]。
湍动能k方程:
湍流动量耗散ε方程:
式中:k、ε分别为湍动能、湍流耗散率;μi、μj分别为沿i、j方向的速度分量;xk为沿k方向的坐标分量;μ、μt、v分别为动力黏度系数、紊流黏度系数、运动黏度系数;G为湍流动能;r为流场半径;Γ为广义扩散系数。
3 条件参数设置
3.1 边界条件
射流泵模型有两个进口,即一个动力气介质入口和一个引射液的吸入口。进口边界条件为动力气入口和吸入液入口的轴向进口速度u,纵向速度v,取动力液入口断面和吸入口断面的平均流速。射流泵有一个出口,射流泵的出口边界条件取出口压力边界。中心边界条件应满足对称性,即在中心边界线处:
壁面采用无滑移边界条件,壁面附近采用边界层理论。
3.2求解器设置与求解
采用三维双精度求解器,采用耦合求解法,算法采用隐式算法,三维,定常流动,采用绝对速度。设置湍流模型(Define-Modles-Viscous Model)模型采用二阶方程的k-epsilon,且使用标准k-ε模型参数。设置求解控制器(solve-controls-solution),选择连续性方程,湍流方程,并采用软件系统默认的计算系数。
3.3 数值模拟结果及分析
根据射流泵排水采气系统实际工况条件,在地面动力泵确定后,气体介质压力基本保持不变,因此对气动力射流泵排水采气效果有显著影响的变量条件只有吸入液流量以及气动力射流泵下入深度,对此分别取吸入液流量为50 m3/d及25 m3/d、出口压力45 MPa及35 MPa,在气体介质7 500不变的条件下进行仿真研究,研究在这两个变量条件下对气动力射流泵排水采气效率的影响规律。
(1)喷嘴3喉管3.8动力气7 500 m3/d吸入流量50 m3/d出口压力45 MPa条件下,动力气速度场分布图如图4所示,静压力场分布图如图5所示。
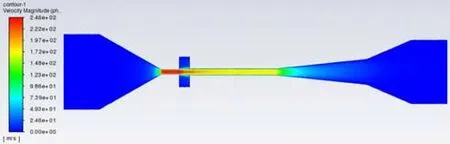
图4 动力气速度场分布图

图5 静压力场分布图
(2)喷嘴3喉管3.8动力气7 500 m3/d吸入流量50 m3/d出口压力35 MPa条件下,动力气速度场分布图如图6所示,静压力场分布图如图7所示。

图6 动力气速度场分布图
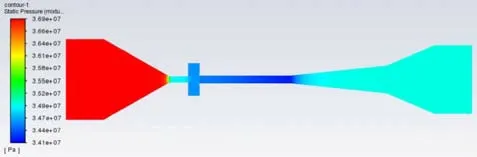
图7 静压力场分布图
(3)喷嘴3喉管3.8动力气7 500 m3/d吸入流量25 m3/d出口压力35 MPa条件下,动力气速度场分布图如图8所示,静压力场分布图如图9所示。

图8 动力气速度场分布图

图9 静压力场分布图
3.4 结果分析
数值模拟结果表明:在动力气流量7 500 m3/d、出口压力35 MPa不变的情况下,吸入流量从50 m3/d降至25 m3/d过程中,动力气压力从36.91 MPa降至36.75 MPa,下降了0.16 MPa;在动力气流量7 500 m3/d、吸入流量从50 m3/d不变的情况下,改变出口压力,动力气压力从46.91 MPa降至36.91 MPa,下降了10 MPa。
4 结束语
(1)在动力气流量,吸入液流量不变的条件下,反排压力降低时,动力气压力也会随之降低,压力下降幅度在10 MPa左右。
(2)在相同动力气流量,出口压力不变的条件下,吸入液流量降低时,动力气压力也会随之降低,压力下降幅度在0.16 MPa左右。
(3)在相同的动力气流量下,改变吸入液流量与返排压力这两个变量参数时,返排压力对动力气压力的影响最大,吸入液流量对动力气压力的影响较小。

