一种基于组合模型的地心运动预测方法

柯 能，朱新慧，王 刃，肖 凯

一种基于组合模型的地心运动预测方法

柯 能1，朱新慧1，王 刃2，肖 凯1

（1. 信息工程大学，郑州 450001；2. 五征集团有限公司，山东 日照 262300）

为了提高地心运动时间序列预测的精度，提出一种基于组合模型的地心运动预测方法：结合灰狼优化（GWO）算法获取最优参数的能力与长短时记忆（LSTM）神经网络处理长时间跨度时间序列的优势，给出调和分析和GWO-LSTM神经网络的组合预测模型；采用调和分析方法分离地心运动时间序列中的模型化成分（长期项和周期项）和未模型化成分，并分别利用调和分析模型和GWO-LSTM模型对2种成分进行预测；然后将2个预测结果进行叠加得到最终的地心运动预测结果。实验结果显示，在预测步长为20 d时，该组合模型预测结果的平均绝对误差在1 mm左右；相比GWO-LSTM模型和调和分析模型，该组合模型的预测精度至少提高了24%和52%；表明提出的方法可以用于地心运动参数预报中。

地心运动；调和分析；长短时记忆（LSTM）神经网络；灰狼优化（GWO）算法；时间序列预测

0 引言

根据国际地球自转服务组织（International Earth Rotation Service, IERS）的IERS2010协议，国际地球参考系（international terrestrial reference system，ITRS）的原点定义为包含固体地球、海洋和大气在内的整个地球系统的质量中心（center of mass，CM）[1]。ITRS的实现，即国际地球参考框架（international terrestrial reference frame，ITRF）的原点在长期尺度上是CM，但在短期尺度上近似为固体地球的形心（center of figure，CF）[2]。由于包含固体地球、海洋和大气在内的整个地球是一个封闭系统，由动量守恒定理可知，大气、地表水、海平面变化等因素会导致CM和CF的相对运动，称CF相对于CM的运动为地心运动[3]。地心运动是实现和维持ITRF参考框架的基础，对于空间大地测量和地球物理学研究具有重大意义[4]。

地心运动的监测和建模是毫米级瞬时地球参考框架的关键问题，然而由于空间大地测量技术观测数据的获取和处理十分复杂，无法得到实时或者准实时的地心运动参数[5]；因此，我们需要利用现有数据建立模型来预测地心运动参数。目前建立地心运动模型的方法主要有调和分析[6]、差分整合移动平均自回归[7]（autoregressive integrated moving average，ARIMA）模型、奇异谱分析[8]（singular spectrum analysis，SSA）、多通道奇异谱分析[9]（multi-channel singular spectrum analysis，MSSA）。调和分析建模简单且稳定，可以在长时间尺度上预测地心运动参数；但是由于其只能对地心运动中的周期项和长期项进行建模并预测，对于难以模型化的部分则无法预测，因此预测精度不高。ARIMA模型本质上是一种线性模型，主要针对平稳的线性时间序列，无法描述地心运动中的非线性关系，经常与其他算法组合使用。SSA方法是一种广义功率谱分析方法，它根据原一维时间序列构造轨迹矩阵，对其进行分解和重构，从而将原时间序列分解为周期项、趋势项和残差项等。MSSA是SSA的一种扩展形式，它顾及通道之间的相关性，同时对多维时间序列进行分析。MSSA和SSA预测的本质是对趋势信号和周期信号进行外推预测，对于残差项则无法预测。近年来，深度学习的发展使其在时间序列预测领域得到了广泛应用。尤其是循环神经网络（recurrent neural network，RNN），因其特殊的网络结构而具有强大的非线性拟合能力，在时间序列预测方面有更强的适应性和更高的预测精度[10]。长短时记忆（long short term memory，LSTM）神经网络作为RNN的改进，有效地缓解了RNN梯度爆炸和梯度消失的问题，同时可以克服RNN的长期依赖问题，善于处理和预测时间序列中间隔和延迟比较长的事件[11]。

地球系统内部的长期性和周期性的质量迁移是引起地心运动的主要原因，分别造成地心的长期性和周期性运动[12]。地心的长期性运动为线性趋势项，可以用线性模型表示。周期性运动分为季节周期性和非季节周期性运动。季节周期性运动主要由陆地水储量变化引起，其中周期项和半年项较为明显，周年项的振幅约为1～4 mm，半年项的振幅在1 mm以内[13]。非季节性周期运动主要由地球潮汐作用以及大气、海洋和陆地水的非潮汐日间活动引起，周期从几小时到18.6 a不等且振幅较小[14]。地心的周期性运动可以用三角函数模型表示。通常的做法是采用调和分析方法拟合地心运动的模型化成分，并建立调和分析模型对地心运动参数进行预测，但是其对于剩余的未模型化成分难以准确建模，这也导致了调和分析模型预测精度不高。为此，本文提出一种基于调和分析和灰狼优化（grey wolf optimization algorithm，GWO）算法-LSTM神经网络的组合预测模型，并利用国际全球卫星导航系统（global navigation satellite system，GNSS）服务组织（International GNSS Service，IGS）第三次重处理（third reprocessing campaign，repro3）提供的地心运动数据进行实验验证。

1 组合预测模型

1.1 组合预测模型的构建

针对地心运动时间序列包含复杂成分，难以准确预测的问题，本文提出一种基于调和分析和GWO-LSTM神经网络的组合预测模型。首先，采用调和分析方法获得地心运动时间序列的模型化成分，并构建时间函数模型，输入待预测历元得到模型化成分预测结果。其次，将原始地心运动时间序列减去模型化成分得到未模型化成分。然后，构建LSTM网络，采用GWO算法求解最优参数，经过训练得到GWO-LSTM预测模型，并输出未模型化成分预测结果。最后，将模型化成分预测结果叠加未模型化成分预测结果，即可得到最终的地心运动时间序列预测结果。

1.2 调和分析

地心运动包含长期项和周期项，可利用时间函数模型表示，残差部分为未模型化成分。地心运动时间序列可表示为[15]

1.3 GWO-LSTM方法

LSTM是一种特殊的RNN神经网络，它引入了“门”结构的概念，通过遗忘门、输入门和输出门可以记住需要的信息和遗忘不需要的信息。这使得LSTM解决了标准RNN存在的梯度消失和梯度爆炸问题，具有长时间的记忆功能，对于长时间时序信息具有良好的处理和预测能力[16]。但是在建立LSTM模型时需要设置复杂参数，通常依靠经验确定，不仅费时而且具有较大的随机性[17]。

GWO算法是一种新型的元启发式群智能优化算法，模拟了大自然中灰狼群体的领导层级和狩猎机制。该算法具有能够自适应调整的收敛因子以及信息反馈机制，能够在局部最优与全局搜索之间实现平衡，相比遗传优化算法、布谷鸟优化算法等经典智能优化算法有更强的搜索能力和更快的收敛速度[18]。本文使用GWO算法搜索确定LSTM网络的最优参数，具体做法是将LSTM网络中学习率、迭代次数和隐藏层单元数模型参数作为GWO算法中狼群的位置坐标，每次预测时通过计算适应度值更新狼群位置以获取模型参数的最优解，最后利用最优参数搭建LSTM模型，对地心运动参数进行预测。GWO算法适应度函数为均方根误差（root mean squared error，RMSE），表达式为[19]

根据预测步长可以将GWO-LSTM神经网络分为单步预测模型和多步预测模型。单步预测模型每次输出一个历元的预测值，然后用此历元的真实值更新GWO-LSTM网络状态，继续进行下一步预测。多步预测模型有递归多步策略和直接多步策略2种训练模型的方法，本文中选用直接多步策略。该策略即每次预测时使用一定数量的样本值作为输入矩阵，往后预测多个历元的值。然后用这些历元的真实值更新GWO-LSTM网络状态，继续往后预测，直到获得所有历元的预测值。

1.4 评价指标

为了验证本文提出的基于调和分析和GWO-LSTM组合模型的预测性能，使用决定系数（coefficient of determination，R2）和平均绝对误差（mean absolute error，MAE）作为预测精度评价指标。其中，决定系数数值越大，模型预测值与真实值的拟合优度越大。平均绝对误差数值越小，模型预测结果越接近真实值[20]。其表达式为：

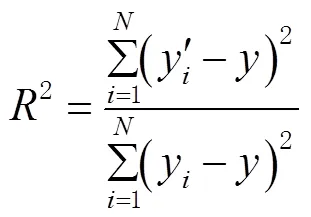
2 实验与结果分析

2.1 实验数据

本文采用的实验数据来自于IGSrepro3提供的地心运动数据（https://cddis.gsfc.nasa.gov/）。IGS利用最新的误差改正模型和数据处理策略，重新分析了1994年以来的全球IGS观测站数据，并运用网平移法得到了地心运动时间序列。由于早期的IGS观测站数据质量较差，导致在此基础上解算的地心运动时间序列误差过大，不利于进行预测研究。因此本文选取了2000—2020年的IGSrepro3提供的地心运动数据，采样间隔为7 d，每个方向共有1096条数据，前70%作为训练集，后30%作为测试集。并采用四分位距法（inter quartile range，IQR）对原始时间序列进行粗差探测与剔除，然后用三次样条插值法补全缺失值。

2.2 参数设置与预测结果

GWO-LSTM模型由输入层、1层隐藏层和输出层组成。输入层神经元个数即输入时间序列长度为80，输出层神经元个数即预测步长为20 d，激活函数设为tanh函数。学习率、迭代次数和隐藏层单元个数利用GWO优化算法搜索确定，其中学习率的取值范围为[0.0001，0.01]，迭代次数的取值范围为[30，300]，隐藏层单元个数的取值范围为[2，100]。GWO优化算法的狼群数量为20，最大迭代次数为50。

依据上文所述参数设置构建组合预测模型，对地心运动时间序列进行预测，结果如图1～图3所示。

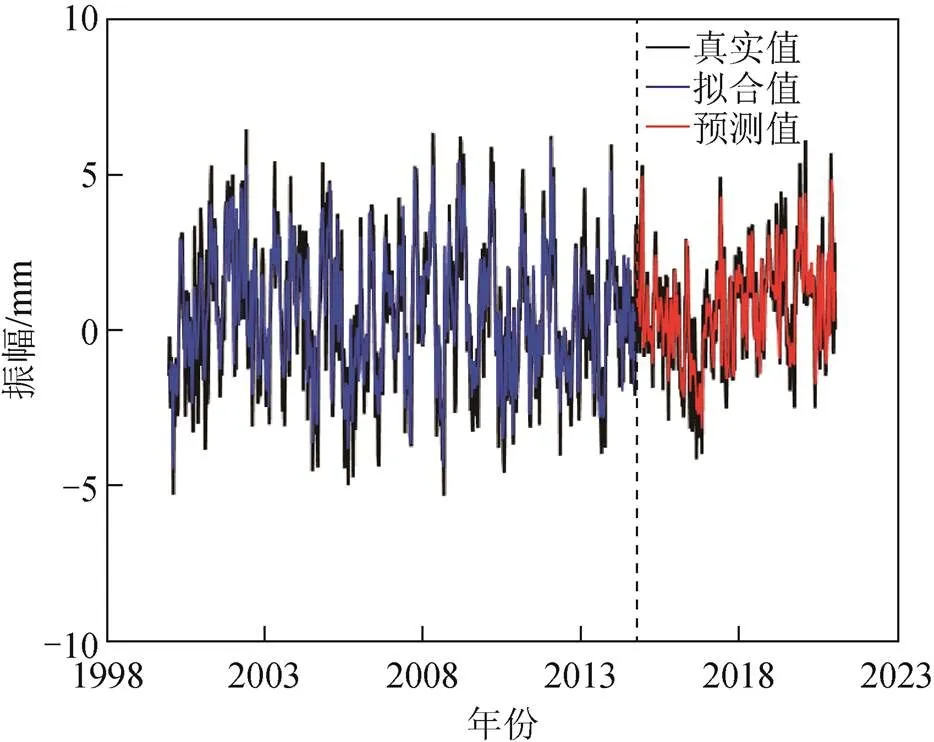
图1 X方向地心运动时间序列预测结果

图2 Y方向地心运动时间序列预测结果

图3 Z方向地心运动时间序列预测结果

图1～图3中，虚线处为2014年8月份，虚线左边是地心运动时间序列训练样本和组合模型拟合值，虚线右边是地心运动时间序列测试样本和组合模型预测值。总体上看预测值与真实值十分接近，预测效果较好。而方向上预测值和真实值有一定偏差，可能是因为方向上噪声含量较高，时间变化规律不明显；方向上训练样本和测试样本一致性较好，波峰和波谷处的预测精度优于和方向，整体预测效果也好于另外2个方向；方向上训练样本噪声含量高，且振幅较大，对最终预测结果产生了一定影响。

2.3 对比分析

为了进一步验证本文提出的组合模型的预测性能，选择GWO-LSTM模型和调和分析模型作对照实验，对地心运动时间序列进行预测。为了更加真实地反映各方法的性能，GWO-LSTM模型采用与本文组合模型相同的输入数据，即调和分析方法分离得到的未模型化成分。并利用式（2）～式（4）分别计算预测值与真实值之间的RMSE、MAE和2，定量分析3种方法的预测精度。如图4～图6所示为组合模型、GWO-LSTM模型和调和分析模型的预测值与地心运动时间序列真实值的对比，如表1所示为3种评价指标的统计结果。

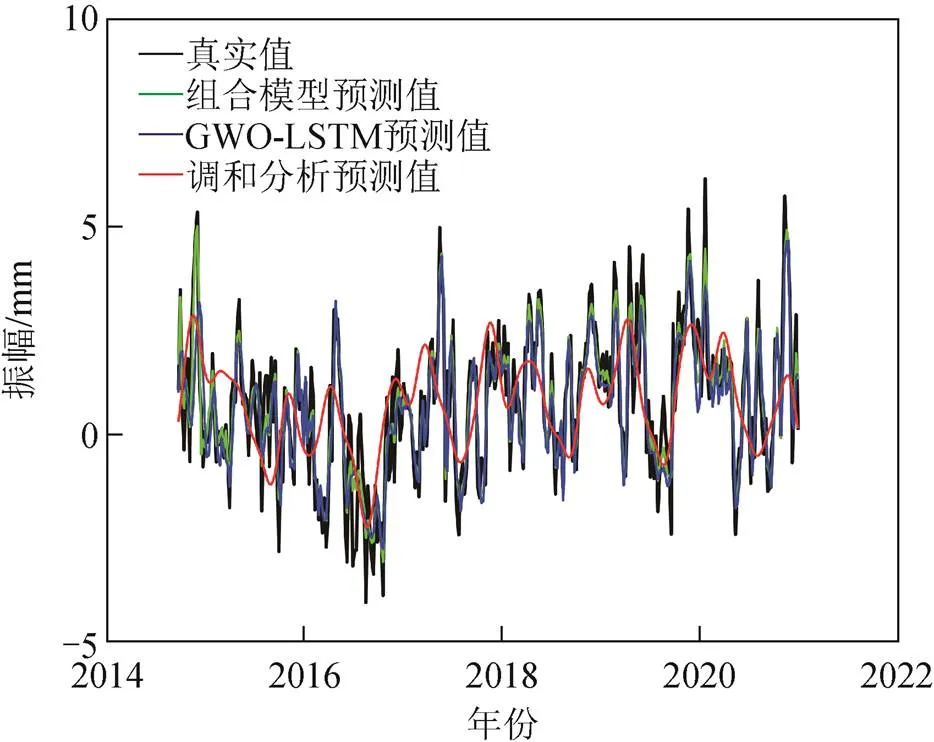
图4 X方向组合模型、GWO-LSTM和调和分析的预测结果

图5 Y方向组合模型、GWO-LSTM和调和分析的预测结果

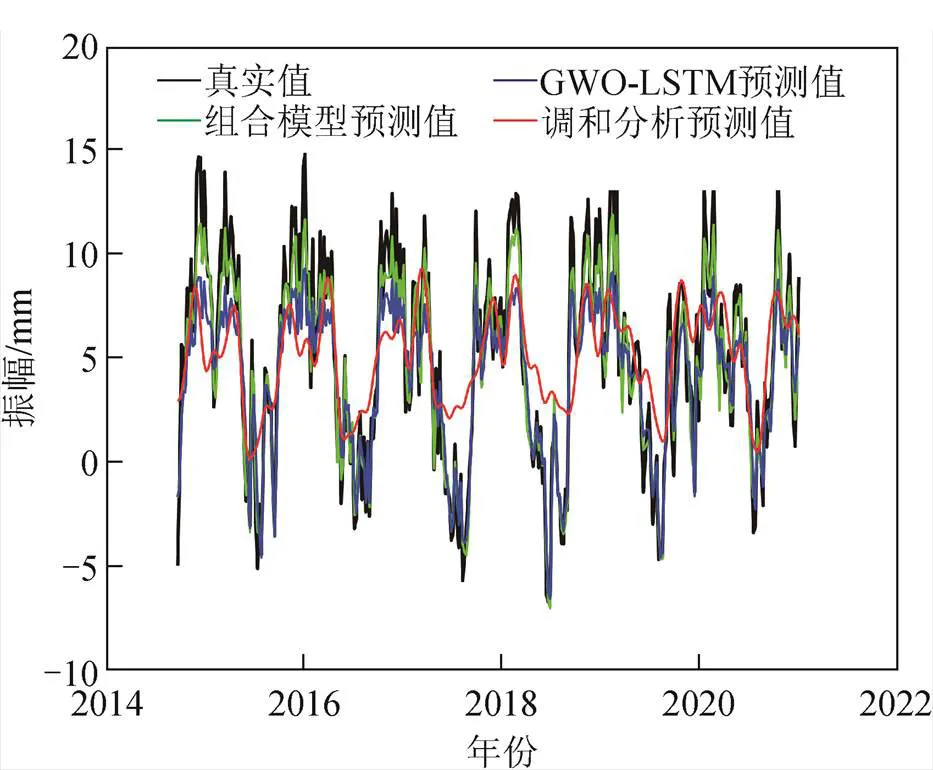
图6 Z方向组合模型、GWO-LSTM和调和分析的预测结果

从图4～图6可以看出，当预测步长为20 d时，本文组合模型和GWO-LSTM模型的预测精度要远高于传统调和分析方模型。调和分析模型在和方向上只能反映出地心运动时间序列的整体趋势，在方向更是出现了较大偏差，预测值的振幅远小于真实值的振幅。GWO-LSTM模型在预测时没有出现较大的偏差，但是与组合模型相比，在波峰和波谷处误差较大。总体来看，组合模型的整体预测效果最好，相较于GWO-LSTM模型和调和分析模型有一定提升。

表1 不同模型预测精度指标

比较表1中数据可知：组合模型和GWO-LSTM模型的RMSE和MAE基本在1 mm左右，而调和分析模型的RMSE和MAE最大可达到3 mm；组合模型的2在0.7～0.9之间，方向可达到0.89，说明方向上拟合优度大，与真实值较为接近；GWO-LSTM模型的2在0.5～0.85之间，上下浮动大，说明GWO-LSTM模型预测稳定性较低；而调和分析模型的2在0.63以下，预测结果与真实值有较大偏差。

相对于GWO-LSTM模型和调和分析模型，组合模型的MAE在方向上分别减小了0.27和0.67 mm，预测精度提高了27%和52%；在方向上分别减小了0.21和0.86 mm，预测精度提高了24%和57%；在方向上分别减小了0.53和1.85 mm，预测精度提高了31%和62%。

3 结束语

本文针对地心运动时间序列包含复杂成分，部分非线性变化难以有效建模、传统预测方法精度不高的问题，提出了一种基于调和分析和GWO-LSTM的组合预测模型，对IGSrepro3提供的地心运动时间序列进行了预测，并采用RMSE和MAE等指标对预测效果进行评估，结果表明：

1）本文提出的组合预测模型避免了传统调和分析模型仅对地心运动模型化成分进行建模及预测的缺点，结合GWO搜索最优模型参数的能力与LSTM处理长时间跨度时间序列的优势，实现了地心运动参数的准确预报。

2）调和分析模型在和方向上只能捕捉到地心运动时间序列的整体趋势，在方向更是出现了较大偏差。GWO-LSTM模型在预测时没有出现较大的偏差，但是在波峰和波谷处误差较大。组合模型在3个方向上均有较高的预测精度，稳定性更好。相对于GWO-LSTM模型和调和分析模型，组合模型的预测精度在方向上提高了27%和52%，在方向上提高了24%和57%，在方向上提高了31%和62%。

综上所述，本文提出的基于调和分析及GWO-LSTM的组合模型无论在预测精度还是稳定性上都优于GWO-LSTM模型和调和分析模型，能够应用于地心运动参数的预报中。

[1] PETIT G, LUZUM B. IERS conventions (2010), IERS technical note 36[M/OL]. (2019-04-01)[2022-07-21]. https://iers-conventions.obspm.fr/conventions_material.php.

[2] 姜卫平, 李昭, 魏娜, 等. 大地测量坐标框架建立的进展与思考[J]. 测绘学报, 2022, 51(7): 1259-1270.

[3] ALTAMIMI Z, REBISCHUNG P, MÉTIVIER L, et al. ITRF2014: A new release of the international terrestrial reference frame modeling nonlinear station motions[J]. Journal of Geophysical Research: Solid Earth, 2016, 121(8): 6109-6131.

[4] 程鹏飞, 成英燕. 我国毫米级框架实现与维持发展现状和趋势[J]. 测绘学报, 2017, 46(10): 1327-1335.

[5] ALTAMIMI Z, COLLILIEUX X, MÉTIVIER L. ITRF2008:An improved solution of the international terrestrial reference frame[J]. Journal of Geodesy, 2011, 85(8): 457-473.

[6] RIES J C. Reconciling estimates of annual geocenter motion from space geodesy[C]// Proceedings of the 20th International Workshop on Laser Ranging. Potsdam, Germany, 2016: 10-14.

[7] SHUMWAY R H, STOFFER D S. ARIMA models[J]. Springer Texts in Statistics, 2011, 90(11): 3886-3896.

[8] 乔灵娜. 基于GPS技术的地心运动时序分析及预测[D]. 山东科技大学, 2019.

[9] JIN X, LIU X, GUO J Y, et al. Multi-channel singular spectrum analysis on geocenter motion and its precise prediction[J]. Sensors, 2021, 21(4): 1403.

[10] 曾国治, 魏子清, 岳宝, 等. 基于CNN-RNN组合模型的办公建筑能耗预测[J]. 上海交通大学学报, 2022, 56(9): 1256-1261.

[11] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780.

[12] WU X, RAY J, VAN DAM T. Geocenter motion and its geodetic and geophysical implications[J]. Journal of Geodynamics, 2012, 58: 44-61.

[13] CRÉTAUX J, SOUDARIN L, DAVIDSON M J F, et al. Seasonal and interannual geocenter motion from SLR and DORIS measurements:Comparison with surface loading data[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B12): ETG 16-1-ETG 16-9.

[14] 谢苏锐, 李斐, 鄢建国. 基于空间大地测量与地球物理方法的地心运动研究与监测进展[J]. 地球物理学进展, 2014, 29(1): 15-24.

[15] 赵德军, 李潭欣, 李婧, 等. DORIS, GPS 和 SLR 空间大地测量技术导出的地心运动规律[J]. 测绘工程, 2015 (12): 21-24.

[16] 刘新, 赵宁, 郭金运, 等. 基于LSTM神经网络的青藏高原月降水量预测[J]. 地球信息科学学报, 2020, 22(8): 1617-1629.

[17] 毛晓娟, 鲍彤, 荀广连, 等. 基于GWO-LSTM的设施蔬菜温室温度预测[J]. 中国农机化学报, 2023, 44(1): 116-123.

[18] MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.

[19] 曲宗希, 沙勇忠, 李雨桐. 基于灰狼优化与多机器学习的重大传染病集合预测研究——以COVID-19疫情为例[J]. 数据分析与知识发现, 2022, 6(8): 122-133.

[20] 石彪, 王海燕, 焦品博. 基于改进GWO-LSTM的船舶主机性能预测模型[J]. 上海海事大学学报, 2022, 43(2): 96-102.

Method for predicting geocentric motion based on a combination model

KE Neng1, ZHU Xinhui1, WANG Ren2, XIAO Kai1

（1. Information Engineering University, Zhengzhou 450001, China; 2. Wuzheng Group Co., Ltd., Rizhao, Shandong 262300, China）

In order to improve the accuracy of geocentric motion time series prediction, the paper proposed a method for predicting geocentric motion based on a combination model: the ability of gray wolf optimization (GWO) algorithm to obtain the optimal parameters was combined with the advantages of long short term memory (LSTM) neural network in dealing with long time span time series to give a combined prediction model based on the harmonic analysis and GWO-LSTM neural network; and then, the modeled components (long-term and periodic terms) and unmodeled component of the geocentric motion time series were separated using harmonic analysis, and the two components were predicted using the harmonic analysis model and the GWO-LSTM model, respectively; finally, the two prediction results were superimposed to obtain the final geocentric motion prediction results. Experimental result showed that the average absolute error of the prediction results of the combined model would be around 1 mm at a prediction step of 20 d, and compared with the GWO-LSTM model and the harmonic analysis model, the prediction accuracy of the combined model would be improved by at least 24% and 52%, indicating that the proposed method could be used in the geocentric motion parameter prediction.

geocentric motion; harmonic analysis; long short term memory (LSTM) neural network; gray wolf optimization (GWO) algorithm; time series prediction

柯能, 朱新慧, 王刃, 等. 一种基于组合模型的地心运动预测方法[J]. 导航定位学报, 2023, 11(6): 22-27.（KE Neng, ZHU Xinhui, WANG Ren, et al. Method for predicting geocentric motion based on a combination model[J]. Journal of Navigation and Positioning, 2023, 11(6): 22-27.）DOI:10.16547/j.cnki.10-1096.20230603.

P228

A

2095-4999(2023)06-0022-06

2023-03-13

国家自然科学基金项目（41804018，42104034）。

柯能（1998—），男，湖北黄冈人，硕士研究生，研究方向为地球参考框架维持。

朱新慧（1979—），女，河南民权人，博士，副教授，研究方向为导航时空基准。