经典测量平差中基本模型和通用模型的参数估计及相互转换
马下平 杨 梅 景 慧 贺小星 林超才
(1. 西安科技大学 测绘科学与技术学院, 陕西 西安 710054;2. 西咸新区自然资源和规划局, 陕西 西安 712000;3. 江西理工大学 土木与测绘学院, 江西 赣州 341000;4. 湖南省有色地质勘查局二四七队, 湖南 长沙 410129)
0 引言
根据含有误差的观测向量,依一定的数学模型,按一定的准则求出未知参数,在数理统计中称为参数估计,在测量中称为平差[1-2]。测量平差中所建立的模型包括函数模型和随机模型。函数模型是描述观测量和待求未知参数之间数学关系的函数模型,而随机模型是描述平差问题中随机量具有先验统计信息的参数及其相互间统计相关性质(先验的方差与协方差)的模型[3-5]。函数模型又分为经典平差和广义平差函数模型。经典平差函数模型有条件平差模型、间接平差模型、带参数的条件平差模型和附有约束条件的间接平差模型[6-7]。
目前,已有很多学者进行了测量平差中基本模型和概括模型之间转换关系的研究。谢波[8]等区分了控制网中的两类不同性质的数据,通过控制网中的观测数据和基准数据分别建立了误差方程和基准方程,建立了概括平差模型。张书毕等[9]用实例指出概括平差模型在解决一些特殊情况时存在不完善地方,并给出改进的解决方法;刘根友等[10]将附有参数先验精度信息的平差问题扩展为参数约束平差,给出了参数约束平差法在数值计算上可以统一自由网平差的新概念;赵超英等[11]在研究两种概括模型的基础上进一步指出附有未知参数的条件平差在某种条件下也是一种概括模型,揭示了各种经典平差模型的内在联系;王新洲[12]通过对条件平差、间接平差、附有条件的间接平差、附有未知数的条件平差和附有限制条件的条件平差5种经典平差模型研究揭示它们之间的区别和内在联系。除了最小二乘算法外,Teunissen[13]等在随机模型中引入了一种递推形式精度的广义卡尔曼滤波器,可以应用于随机模型被错误指定的情况;Felus[14]提出了总体最小二乘法,解释了如何使用广义最小二乘法将误差包含在所有变量中,介绍了总体最小二乘问题及其公式和求解步骤。康壮[15]在以后的参数平差模型中引入线性泛函,构建其统一的几何模型。
目前基于最小二乘算法的经典平差仍然很受欢迎,但以往对经典平差模型中参数的估计,往往是一种模型进行一次公式推导,为了克服这种推导方法所产生的不必要的麻烦,本文以经典测量平差中的条件平差和间接平差这两个基本平差方法的函数模型为基础,详细推导带参数的条件平差、附有约束条件的间接平差函数模型中的参数估计公式,总结出了经典测量平差的通用函数模型,推导出该模型的参数估计公式,并证实了通用平差模型和经典测量平差模型之间的关系。
1 经典测量平差模型
函数模型分为线性模型和非线性模型两类。当函数模型为非线性函数时,总是将其用泰勒公式展开,并取其一次项化为线性形式。高斯—马尔柯夫模型(G-M模型)是测量平差中最基本、最典型、应用也是最广的一种线性模型。根据G-M函数模型,可以得出以下几种经典测量平差中常用的函数模型。
1.1 间接平差模型
间接平差是通过选定t个独立的未知向量,并将m个观测值分别表示成这个参数的函数,其函数模型为
(1)
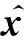
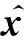
将式(2)代入式(1),得
(4)
可知JA为一幂等阵,I-JA也是幂等阵,有
(5)
1.2 条件平差模型
条件平差主要是利用观测值之间的几何条件建立的方程为函数模型的平差方法。设观测值之间的几何条件的个数为r个。则函数模型可表示为
(6)
式中,B为r×m阶系数矩阵,rank(B)=r;wB为r维闭合差向量。

1.3 带参数的条件平差模型
在条件平差中,加入u个独立的未知参数,并建立未知参数与观测值之间的几何关系为函数模型的平差方法称为带参数的条件平差法。函数模型为
(9)
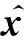
式(9)可以分两步解算,得出f的改正数向量Vf、f的协因数矩阵Qf和权阵Pf分别为
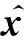
(13)
由式(10)写出Vf的计算式为
(14)
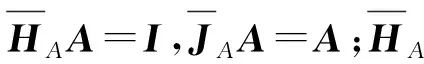
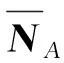
当需要获取观测量改正数向量V而不是Vf时,需要将式(14)代入式(9),得
(15)

由式(7)得
(16)
1.4 附有约束条件的间接平差模型
在间接平差中,如果未知参数之间满足以下s个约束条件
(17)
则组成附有约束条件的间接平差的函数模型为
(18)
式中,C为s×t阶系数矩阵,rank(C)=s;wc为s维约束方程常数项。
分两步解上两式,先解第一式,这是间接平差模型,由式(2)得
(19)
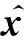
(20)
将式(20)代入式(18),得
(21)
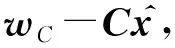
(22)

设JC=HCC,则式(22)写为
(23)
将式(23)代入式(20)并顾及式(19),得
(24)
将式(24)代入式(22),化简得
(25)
2 通用平差模型
2.1 模型概述
(26)
式中,B为g×m阶系数矩阵,rank(B)=g;A为g×t阶系数矩阵,rank(A)=t;C为s×t阶系数矩阵,rank(C)=s。
不难看出,间接平差、条件平差、带参数的条件平差和附有约束条件的间接平差模型是通用平差模型的特殊情况。
当B=-I,C=0,f=l时,通用平差的函数模型变成间接平差的函数模型,式(26)变为式(1);当A=0,C=0,f=wB时,通用平差的函数模型变成条件平差的函数模型,式(26)变为式(6);当C=0时,通用平差的函数模型变成带参数的条件平差的函数模型,式(26)变为式(9);当B=-I,f=l时,通用平差的函数模型变成附有约束条件的间接平差的函数模型,式(26)变为式(18)。因此,称式(26)为通用平差模型。
分两步解式(26),设
(27)
其权阵为式(12)。将上式代入式(26),得
(28)
这是附有约束条件的间接平差模型。
(29)
由式(7)写出Vf的计算式为
(30)
由式(14)直接写出V的计算式为
(31)
将Vf代入上式,得
(32)

式(28)也可以按照求解式(18)的第二中推导方法,其估计出的未知参数计算公式与式(29)完全相同。
从以上可知:间接平差模型和条件平差模型是测量平差的基本模型,由基本模型的计算公式,可以导出带参数的条件平差、附有约束条件的间接平差和通用平差模型的计算公式。本文从基本模型出发,导出了其余3种模型的计算公式,可以从通用平差模型出发,导出其余4种模型的计算公式。
2.2 通用平差模型可行性验证
2.2.1 实验数据
现结合实际的实验数据,通过比较分析不同模型计算的各待定点的高程平差值对模型进行可行性和性能分析。如图1为一水准网,已知点高程HA=105.016 m,HB=106.016 m,高差观测值h1=+1.359 m,h2=+2.009 m,h3=+0.657 m,h4=+1.012 m,h5=+0.363 m,h6=+0.238 m,h7=-0.595 m。 路线长度S1=1.1 km,S2=1.7 km,S3=2.4 km,S4=2.7 km,S5=2.3 km,S6=1.4 km,S7=2.6 km。现采用条件平差和间接分别进行解算。

图1 水准网示意图
(1)条件平差:列出条件方程式、定权、组成法方程并解算,计算高差观测值的改正数进而求得各待定点的高程的平差值。
(2)间接平差:选参数并计算参数近似值、定权、列平差值方程和误差方程,组成法方程并解算,计算未知参数的平差值进而求得各待定点的高程平差值。
2.2.2 结果的分析与比较
表1列出了条件平差和间接平差两种模型的计算结果。
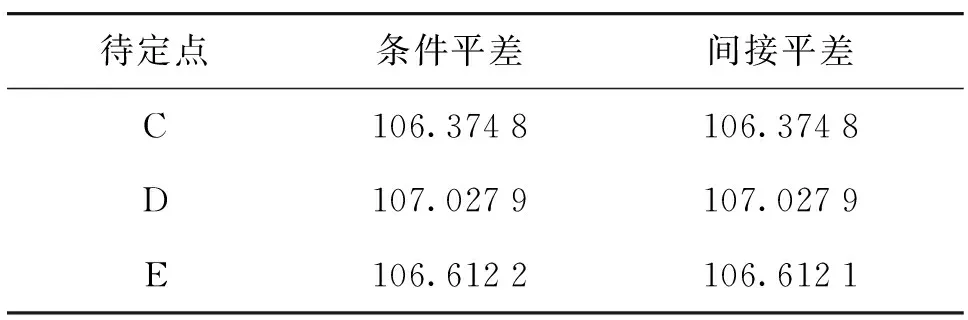
表1 高程平差值计算结果 单位:m
由表1可得条件平差和间接平差所求得的结果完全相同,E点高程平差值有差值是因为进位误差引起的,可忽略不计,即证明条件平差和间接平差都是通用平差模型的特殊情况。
3 结束语
本文通过对经典测量平差的函数模型及通用函数模型计算公式的推导,得出以下结论:
(1)间接平差和条件平差是最基本的经典测量平差模型,由这两个平差函数模型的计算公式可以推导出带参数的条件平差模型、附有约束条件的间接平差模型和通用平差模型的计算公式。
(2)通用平差模型是其余四种平差模型的一般形式,其他四种平差模型是通用平差模型的特殊形式;由通用平差模型的计算公式可以推导出其余4种模型的参数估计公式。
(3)本文虽然由基本模型推导了通用平差模型,也给出了他们之间的转换关系。但本文推导是基于最小二乘原理,对于其他参数估计方法平差模型之间的等价性证明将是未来研究的重点。

