超低品位磁铁矿矿岩破碎能耗优化研究
杜广盛 武海龙 高云峰 陈世江
(1.内蒙古科技大学矿业与煤炭学院,内蒙古 包头 014010;2.内蒙古自治区矿业工程重点实验室,内蒙古 包头 014010;3.乌拉特前旗元大商贸有限责任公司,内蒙古 巴彦淖尔 014400)
矿岩破碎是露天矿开采及加工过程中的主要能耗之一。采下的矿石须经粗碎、细碎等环节进行选矿作业,剥离的废石若能进行充分利用既可减少堆弃场地,又有一定的经济效益。在矿岩破碎过程中,其能耗指标是影响经济效益和绿色生产的主要因素之一。不少学者在研究破碎能耗的过程中,通过对现场实际破碎效果及能耗情况的分析得出了三大破碎功耗理论[1-4],分别从面积、体积、裂缝的角度,对岩石破碎过程中的功耗进行了统计并得出相应的经验计算公式,明确了破碎能耗与破矿粒度及矿石强度性质的关系。基于此,本研究重点分析岩石物理力学属性参数与破碎能耗的关系,以及矿山实际设备不同破碎比的能耗规律,进而优化破碎粒度,降低矿岩破碎能耗。
对于岩石物理力学属性与破矿能量问题,谢和平、鞠杨等学者[5-7]对岩石破碎能量耗散体系进行了分析,提出了基于能量耗散原理的岩石强度理论与破坏准则,强调了岩石破碎是由于外部能量输入使得岩石内部产生了损伤所致,认为岩石本身物理力学属性与其破坏时耗散的能量存在很大关系。然而岩石破碎过程中具体的能耗情况影响因素极为复杂,且试验检测手段受限。鉴于此,部分学者通过声发射等能量监测手段对岩石破碎过程中的能量进行监测和分析[8-10],有效确定了外部输入能量的转移传递情况,明确了岩石质量与声发射能量的关系,为能耗分析提供了依据。近年来,一些学者研究了岩石破坏过程中的能耗情况[11-18],着重分析了不同加载情况下岩石内部能量的耗散利用情况和不同岩石力学属性对能耗的影响,研究结果表明:岩石质量参数能够有效表征岩石破碎能耗指标。针对破矿方式和矿石粒度能耗关系的问题,文献[19-23]分别研究了破矿颗粒分布及破矿方式和能耗情况,结果表明:不同破矿方式和颗粒特征都会对破矿能耗有所影响,但整体上单次破碎比与能耗呈正相关,且单次破碎比越大,能耗越高。
基于上述成果,结合某露天矿山实际情况,本研究针对不同矿岩进行力学试验从而构建矿岩质量参数,并引入破碎能耗公式求解能耗指标,进而对矿山能耗进行优化分析。同时以矿山实际设备为基础,分析多级破碎中的能耗规律,并对能耗指标进行求解,较为准确地优化矿山破碎能耗。
1 岩石力学试验
不同力学性质岩石破坏时的能量消耗有较大差异,为此,本研究对该矿山采场采出的矿石和上下盘岩石分别进行了力学性质试验。由于破矿形式有所不同,对岩石进行了单轴抗压、巴西劈裂抗拉、双轴抗剪等较为全面的测试。
1.1 岩石试件制备
(1)针对矿山不同区域的岩石性质差异,选择从采场矿体中部平台上选取部分岩体,在地质图上对应其岩性,并对上下围岩和矿石进行分类。对取回的岩石进行加工,以制成符合实验室单轴抗压试验要求的试件。
(2)岩样加工过程中将切割机刀片相对位置调整为100 mm,切割后获得上下端面较为平整的岩块;然后利用立式取芯机在规整的岩块表面进行钻取切割。为保证制备的试件完整且尺寸和表面条件达标,在取芯的过程中钻头给进速度选取4 mm/min;最后采用端面磨平机对试件两端面进行平整度校准。试件高径比保持为2∶1,直径误差不超过0.3 mm,两端面平整度误差保持在0.05 mm以内。试件制备过程及结果见图1。

图1 试件制备过程Fig.1 Preparation process of specimens
1.2 岩石力学性质测试试验流程
(1)单轴抗压试验。岩石单轴抗压强度采用wance106微机控制电液伺服万能测试机进行测定,最大垂直加载力为1 000 kN,试验采用压力控制方式,初始加载给入压力设置为100 N,压力速度为500 N/s,破坏力识别为15%,在到达极限载荷强度时自动卸载5 s,以保证试件破坏后及时撤去加载力。
(2)岩石单轴压缩变形试验。采用应变数值采集仪、应变片、位移采集器等记录试件在加载过程中的形变状态。分别将应变片贴在岩石试件表面,垂直和水平方向均进行了监测。
(3)岩石巴西劈裂抗拉强度试验。采用巴西劈裂测定岩石抗拉强度,根据要求的劈裂方向,通过试件直径的两端,沿轴线方向画两条相互平行的加载基线,将试件放置在加载板上,调整中心位置,使试件不产生应力集中,以0.3~0.5 MPa/s的速度加载直至破坏。
(4)岩石双轴抗剪强度试验。将制备好的试件放置在剪切模具中,模具由硬质合金钢制成,具有较高的强度,变形量很小。本次试验保持一致的法向力,设置为2 kN;当法向力稳定后再加载切向载荷,不断对切向载荷进行监测,以0.05 mm/s位移进行加载直至破坏。

图2 岩石力学试验Fig.2 Rock mechanics test
1.3 试验结果分析
根据测试结果,分别进行单轴抗压强度、抗拉强度、抗剪强度、弹性模量等指标计算。
单轴抗压强度计算公式为

式中,σc为岩石单轴抗压强度,MPa;P为最大破坏载荷,N;A受载试件的横截面积,mm2。
弹性模量计算公式为

式中,E为弹性模量,GPa;σ为应力,MPa;ε为应变,可进行如下计算:
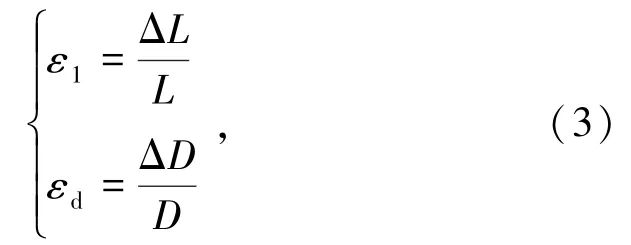
式中,ε1为各级应力的轴向应变值;εd为与ε1同应力的径向应变值;ΔL为轴向变形平均值,mm;ΔD为径向变形平均值,mm;L为试件高度,mm;D为试件直径,mm。
抗拉强度计算公式为

式中,σt为岩石抗拉强度,MPa;P为试件破坏载荷,N;D为试件直径,mm;h为试件厚度,mm。
抗剪强度可进行如下计算:

式中,τ为作用于剪切面上的剪应力,MPa;P剪为剪切载荷,N;A剪有效剪切面面积,mm2。
根据式(1)至式(5),相关参数计算结果见表1。
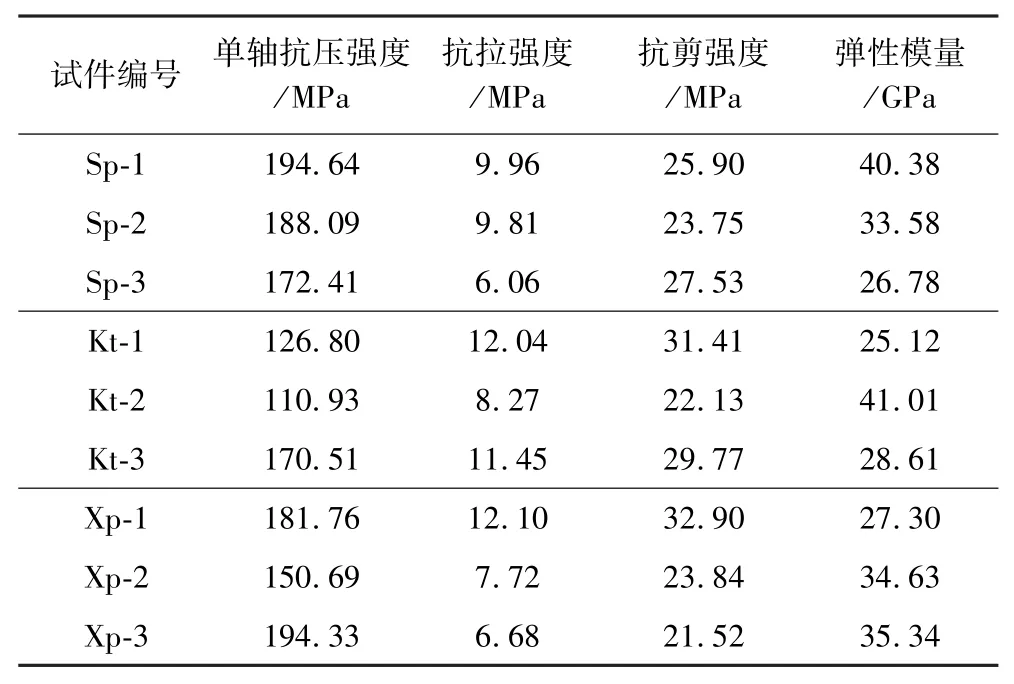
表1 岩石力学性质试验结果Table 1 Test results of rock mechanical properties
对计算结果进行了统计,3组试验取平均值如图3所示。其中,试件组1、2分别为上下盘围岩分组,试件组3为矿石分组,上下盘围岩单轴抗压强度明显大于矿石强度,且矿石强度约为围岩的75%;弹性模量变化趋势与单轴抗压强度相同,也呈现围岩弹性模量大于矿石的特征。
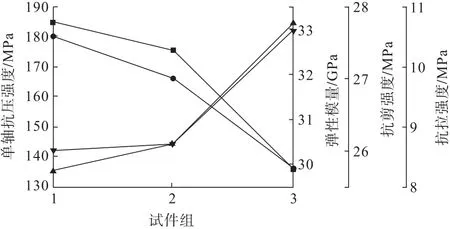
图3 不同矿岩力学参数对比Fig.3 Comparison of the mechanical parameters of different minerals and rocks
由图3可知:相对于上下盘围岩,矿石单轴抗压强度较低但抗拉强度和抗剪强度较高,说明矿石相对围岩显延性;而围岩单轴抗压强度较高,抗拉和抗剪强度较低,说明其显脆性。
2 矿石破碎能量分析
岩石在破碎过程中需要受到外部的能量输入才能进行相应的失稳开裂,不同的挤压破碎方式所输入的能量也有所不同,不同的开裂形式所吸收的能量也有较大区别,并且岩石的物理力学性质对能量输入和保存也有一定的影响。近年来,部分学者从能耗角度对岩石破碎能量理论进行了分析。
2.1 破岩能耗理论
2.1.1 吉尔皮切夫和F.基克学说——体积学说
矿石破碎过程中具有形变储能等作用,在矿石破坏后其整体体积没有发生改变而形态有所变化。设A为矿石破碎所需能量与其体积或质量的比值,对于单位体积岩块,其计算公式为[2]

式中,k1为比体积功,产生一个单位体积形变所做的功;Δv为微元破碎体积变化量。
将破碎过程视为多次破碎的叠加,可以推导出:
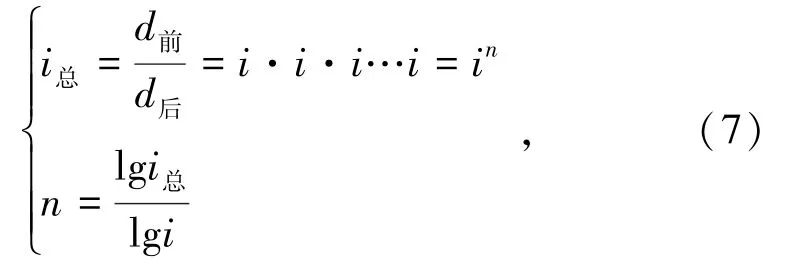
式中,i总为总破碎比;i为微分每级破碎比;d前、d后为破碎前后粒径,mm;n为微分的破碎级数。
当破碎一定体积矿石时,矿石总体的体积变化量可表示为

将式(8)代入式(6)中可得总破碎功耗情况:
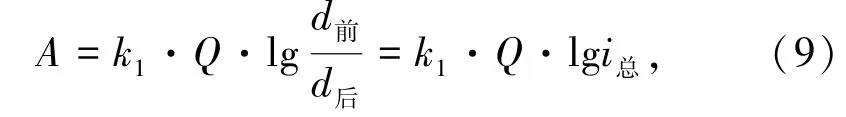
式中,Q为进料体积,m3。
破碎物料通常为混合物料,可通过下式求出单一矿石能耗W对k1进行优化:

式中,k为破碎功参数;wx为每级能耗,J;W为总能耗,J;c为岩块强度属性参数。
在岩石破碎过程中k矿、k岩受岩石本身物理力学属性影响,将式(11)参数按顺序代入式(12)中可以求得k1关于σ和E的表达式。对k1进行分析求解可以得出式(13):

式中,F1、F2分别为不同岩块载荷,N;x1、x2为作用力下的位移,mm;σ1、σ2分别为岩块强度;S为试件受力面积,mm2;L为试件位移方向的尺寸,mm;E1、E2为试件弹性模量;m为比例系数。
可以看出k1受岩石单轴抗压强度σ和弹性模量E的影响,因此在岩块强度属性存在差异时会对整体破碎能效产生影响。
2.1.2 F.C邦德及王文东裂缝学说
根据碎矿、磨矿设备试验得到的资料[2],整理成如下经验公式:

式中,Wi为邦德功指数,是当物料尺寸为0.1 mm时的功耗;F为进料尺寸,mm;P出为出料尺寸,mm。
通过球磨机试验进一步确定Wi值:
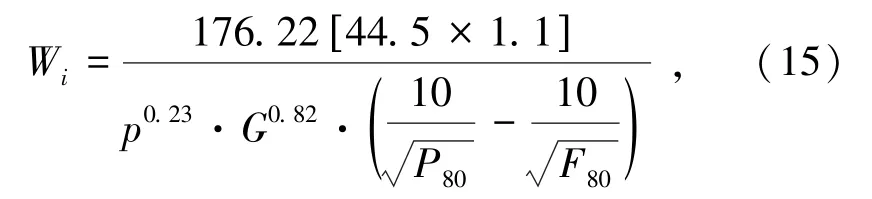
式中,p为筛孔尺寸,mm;G为新生筛下物料质量,g;P80、F80为出料和进料80%过筛尺寸,mm。
通过对矿石的试验可以得出p为0.15 mm;G约为4 g;P80、F80分别为0.125、3.3 mm;最终计算得Wi约为20。
2.2 岩石力学性质评价
经过本研究试验得出,矿石和围岩的力学性质分别表现为延性和脆性。选取岩石力学性质中抗压强度σc与抗拉强度σt的比值作为评价岩石脆性和延性的指标b,即b=σc/σt。代入试验数据计算可得,b值分别为21.54、12.89、20.34。由式(13)可以看出σ为岩块强度,当采用混合经验公式时可以将岩石脆性指标b作为平均指标代入公式中。即σ1/σ2=b1/b2。此时利用岩石物理力学性质参数选取单位强度1进行对比,可以进一步求出3种不同岩性的k1值分别为14.12、5.54、12.97。由k1值的变化可以看出,当其他参数不变时,破碎围岩的能耗远大于破碎矿石的能耗。
2.3 矿岩初破不同粒径能耗分析
根据矿山破碎设备的实际情况,可知在初破工序时,进料岩石块度平均尺寸为400 mm,出料口为95~165 mm。
通过破碎机理可知,在破矿形式不变的条件下,破碎料强度也保持一致时,k1、Q值取1。破矿能量受矿物颗粒变化影响。由粗料破碎理论式(9)可知,出料粒径为95 mm时A为66.62;当出料粒径为165 mm时A为29.55。此时可以看出破矿粒度对能耗影响非常大。
对不同出矿粒度进行分析,结果如图4所示。由图4可知:随着出矿颗粒增大,能量消耗比逐渐减小,出矿颗粒为165 mm和95 mm时能耗比为29.55和66.62,并且减小速度降低,即出矿颗粒从95 mm变化为100 mm时能耗比降低了4.37,而出矿颗粒从160 mm变化为165 mm时能耗比降低了1.57。
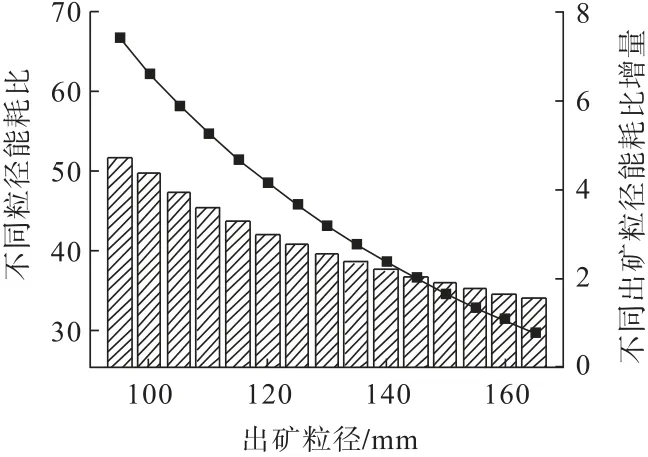
图4 出矿粒度与能量耗散比的关系Fig.4 Relationship between ore size and energy dissipation ratio
2.4 矿岩多级破碎不同粒径能耗分析
根据矿山实际破矿工艺及设备参数可知,主要产出为一定粒径的石子,因此本研究采用F.C邦德(Bond)及王文东裂缝学说(1952)[2]分析式(14)发现,显然该公式受到岩石力学性质和岩石破碎块度影响,当Wi取20且保持不变时,能耗受块度比变化的影响。分别将不同的粒径代入式(14)进行计算可以得到如图5所示的变化曲线。由图5可知:粒径差值越小能耗越低,随着粒径差值逐渐增大消耗过多的能量无法将颗粒进一步破碎,造成一定的能量损失,因此选取逐级破碎效果更好。
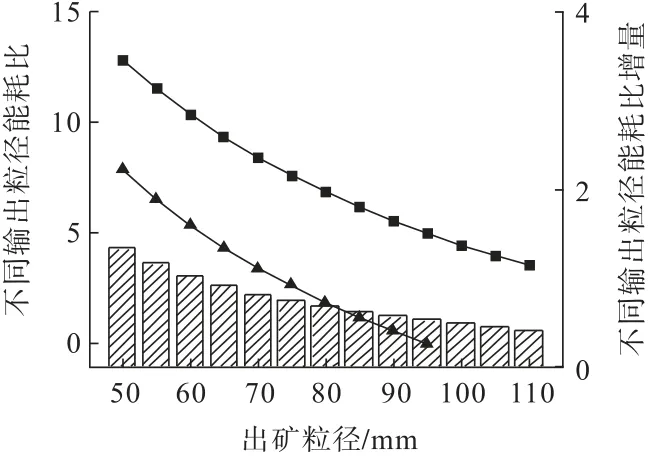
图5 出矿粒度与粒度差值能耗比关系Fig.5 Relationship between ore size and energy consumption ratio of particle size difference
2.5 矿岩破碎总能耗优化
针对矿山实际工程需求,该矿山后续破碎共分为4级,且随着不同破碎工艺产出不同粒径的石料。破碎后最终产出物料为3 mm石子,因此后4级总破碎比i总=3/d1,其中,d1为初破后的颗粒尺寸。通过对图4、图5分析可知:当单极破碎过多时会大量消耗能量。当进行初破之后,将后续4次破碎粒径平均分布在整个工艺中,即破碎比i总=(i单)4。而初破后不同的粒径对后续破碎有着较大影响,当d1为95~165 mm可以求得i总为1.82%~3.16%,此时i单为36.7%~42.2%。通过式(14)求得后续4级能耗。由于初级破碎与后4级破碎设备的差异,通过矿山数据调查得出初破与后续破碎能量利用率分别为0.8和1.5。因此对初级破碎能耗进行加权求和可得出整体工艺能耗比情况,如图6所示。由图6可知:当初破粒度为125 mm时,后续破碎保持40%左右的破碎比时能耗比最低。
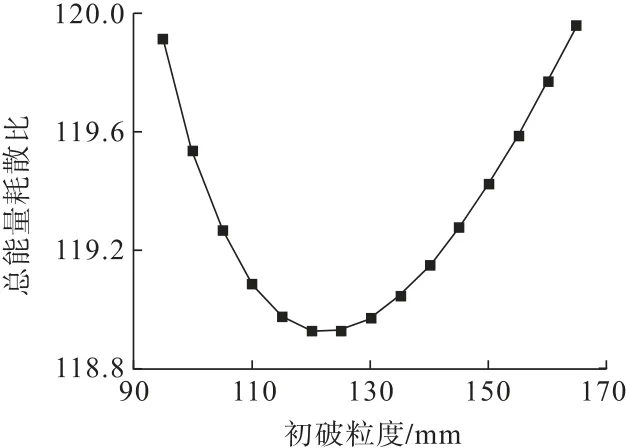
图6 不同初破粒度下总能耗比Fig.6 Total energy consumption ratio under different initial breaking particle sizes
3 结 论
针对矿山矿岩破碎的能耗问题,以内蒙古中部地区某露天矿为例,采用室内试验对矿岩质量进行了测定并结合矿岩破碎理论,进一步分析了矿岩质量与多级能耗间的关系。所得结论如下:
(1)通过对经典能耗公式中引入结合了岩石强度与脆性参数的岩石质量参数b,有效地计算出不同质量参数矿岩在破碎过程中的能耗指数,为能耗优化提供了更为合理的依据。
(2)通过对不同矿岩进行试验可以计算出岩石质量参数b,结合矿山实际破碎工艺采用经典能耗公式进行计算,可以得出破碎围岩能耗高于破碎矿石,应分时段破碎;在多级破碎能耗优化中,矿岩初破应破至125 mm,后续多级破碎时应破碎至当前粒径的40%左右时能耗较低。
(3)结合实际生产情况,不同的破矿形式被用于不同的破碎阶段,这与矿岩质量共同构成了破碎能耗指标,而常用的能耗公式中对此研究不足,因此结合破碎形式和矿岩质量的修正系数对能耗指标的表征更为精确。

