角柱形掏槽孔布置及毫秒延时爆破效果分析与应用
段宝福 柴明星 张正欣 孙宗军
(1.山东科技大学土木工程与建筑学院,山东 青岛 266590;2.山东省土木工程防灾减灾重点实验室,山东 青岛 266590;3.青岛瑞翰科技集团,山东 青岛 266061)
钻爆法作为岩巷掘进中的主要技术,对巷道掘进效率的提升有重要影响。特别是在中深孔爆破掘进中,直眼掏槽的爆破进尺和效率高于斜眼掏槽,而在多数工作面受限的巷道中,直眼掏槽更是主要的掏槽方式[1]。
为了提高巷道掘进效率,不少学者对含空孔直眼掏槽爆破进行了深入研究。LANGEFORS等[2]总体分析了直眼掏槽的碎岩机理,构建了空孔直径影响爆破作用的半理论半经验公式。STEPANOV等[3]通过理论和模型试验,探究了同时起爆平行炮孔的爆破效果,得到了该种爆破方式下的最大碎岩范围。SHAPIRO等[4]对不同形状的掏槽爆破技术进行了分析,得出了最佳形状的掏槽孔布置方案。李洪伟等[5]通过电子雷管的模型试验,研究了直眼掏槽爆破掏槽孔与辅助孔间延期时间对掏槽爆破效果的影响,给出了孔间最佳延期时间范围,并通过对直眼掏槽爆破过程进行数值模拟,验证了最佳延期时间。王远来等[6]针对直眼掏槽孔打孔数量过多的问题,通过理论分析确定了炮孔和空孔间距的取值范围,通过数值分析和工程实例得出空孔处应力集中的变化规律,并给出适用的炮孔直径和孔间距。汪平[7]开展了单空孔直眼掏槽爆破、三空孔直眼掏槽爆破和三空孔直眼掏槽爆破改进共3种方案的现场爆破效果对比试验,试验结果表明:适当提高空孔的数量,增大掏槽爆破的补偿空间,可显著提高巷道爆破掘进效率。范兴俊[8]对直眼掏槽爆破的各种形式进行了总结,依据爆轰波理论和爆轰波衰减规律设计了九孔菱形中部间隔装药的掏槽方式,并结合LS-DYNA数值模拟方法进一步确定了该方式的粉碎圈和裂隙圈范围,从而验证了掏槽方式的可行性。
现有研究大多倾向于掏槽孔爆破半径和破碎机理,在角柱形掏槽孔间距、布孔方式和起爆方式分析方面有待进一步深入。本研究通过理论推导,得出了理论最适宜孔间距,据此建立不同孔间距、不同布孔方式和不同起爆方式的数值模型,并结合工程实例进行了综合分析,分析结果有助于提高岩巷掘进效率和经济效益。
1 最适宜爆破孔和空孔间距理论计算
现阶段,常用计算裂隙的经验公式为
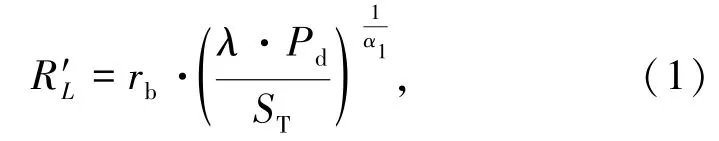
式中,R′L为裂隙圈半径,mm;rb为爆破孔半径,mm;Pd为不耦合装药爆腔压力,Pa;ST为岩石抗拉强度,Pa;α1为应力波衰减系数;λ为侧向应力系数,可进行如下计算
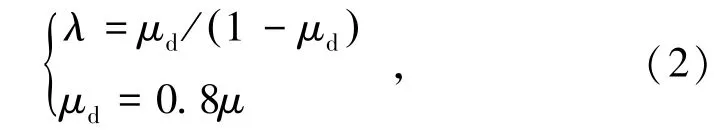
式中,μd为动态泊松比;μ为静态泊松比。
式(1)、式(2)中相关参数取值见表1。
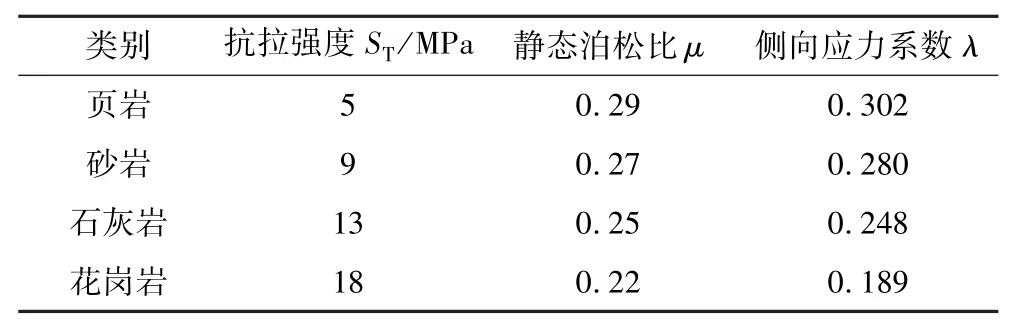
表1 岩石材料相关参数Table 1 Parameters related to rock materials
式(1)中,Pd可进行如下计算:
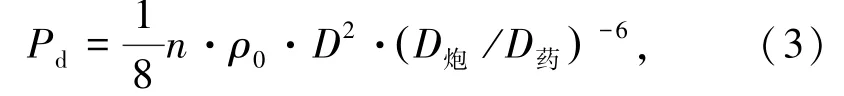
式中,ρ0为炸药密度,kg/m3;D为炸药的爆轰速度,km/s;D炮为炮孔直径,mm;D药为药卷直径,mm;n为压力增加系数。
确定爆破孔和空孔间距还需要考虑空孔处的裂隙区,即[9]:
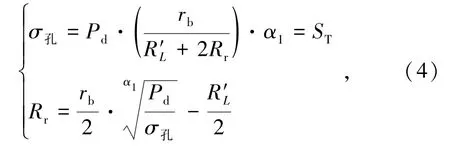
式中,σ孔为孔壁切向应力,N;Rr为反射拉伸波形成的裂隙半径,mm。
在工程实践中,掏槽孔的最优参数需要满足多种因素和限制条件,方可适应复杂的工程环境。为有效防止碎石填满空孔,导致能量浪费,并满足补偿空间理论[10]的要求,本研究考虑到爆破孔和空孔的最小间距,计算公式为[11]

式中,R1为考虑岩石碎胀的爆破孔和空孔间距,mm;rd为空孔半径,mm;h为装药系数,即装药长度与炮眼长度之比,一般取0.7[12];K为岩石膨胀系数。
通过式(5)计算,能够得出符合补偿空间理论的爆破孔和空孔间距,依据该式得出的限制间距,有助于进一步获得最适宜间距取值。
2 直眼掏槽爆破数值模型
2.1 工程背景
本研究以山西天地王坡煤业有限公司3206高抽巷为例进行分析。该巷道设计长度为2 162.5 m,是3206工作面瓦斯抽放专用巷。3206高抽巷断面形状为矩形,巷道掘进断面宽3.5 m、高3.4 m,掘进断面面积11.9 m2。工作面岩石以石英砂岩和砂质泥岩为主,坚固性系数为4~8,属中硬岩石。
结合巷道基本情况以及表1,得出R′L=264 mm,Rr=68 mm,R1=111 mm。进一步计算得,Rmax=R′L+Rr=332 mm,Rmin=111 mm。本研究选择R=Rr+R1=179 mm作为最适宜间距,是因为该值处于最大和最小值范围内,满足补偿空间理论等因素的限制条件,作为最适宜间距最为合适。
对于理论得出的最适宜间距还需要多种方式进一步验证其适用性。因此假定最适宜间距为179 mm,运用数值模拟软件建立多种数值模型进行分析,在此基础上,结合工程实际爆破效果予以评价。
2.2 数值模型参数和尺寸选择
数值模型为边长1 000 mm、高10 mm的立方体,采用solid164单元类型,岩石和空气部分占据整个模型,爆破孔和空孔直径均为42 mm,模型网格按照10 mm划分,四周设置无反射边界,约束上下面的竖向位移。
爆破孔和空孔的最小间距采取140、170、200、230 mm 4种间隔,根据不同的延时次数,又分为同时起爆、两段毫秒延时起爆和三段毫秒延时起爆3种情况,并且每种延时情况又分为多种布孔方式,如图1~图3所示。理论上说,虽然空孔直径越大越好,但是为了施工方便,本研究使空孔和爆破孔的直径相同。对于同时起爆,图1中,模型1横向爆破孔间距是纵向爆破孔间距的2倍,模型2横向和纵向爆破孔间距均相同。对于两段毫秒延时起爆,模型1、模型2与图1中模型相同,起爆方式不同;模型3炮孔间距相同,炮孔间距为炮孔和空孔间距的2倍;模型4爆破孔与模型3相同,空孔的横纵距离均为爆破孔间距的1/2。对于三段毫秒延时起爆,模型1、模型2与图2中模型3、模型4相同,起爆方式不同。
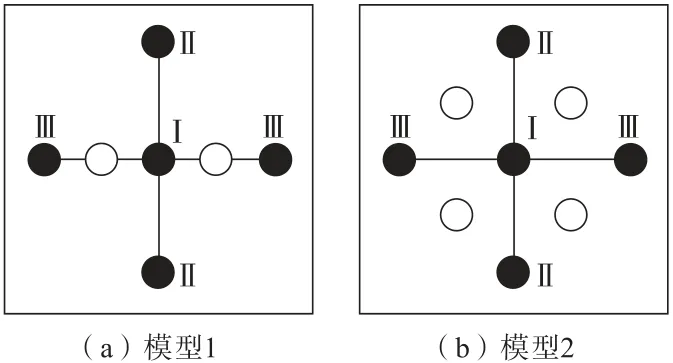
图1 同时起爆模型Fig.1 Simultaneous detonation models
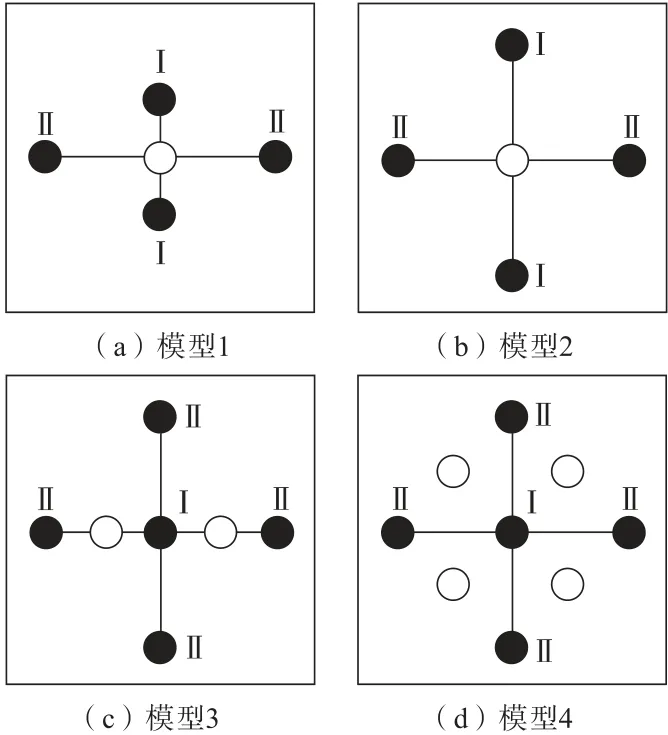
图2 两段毫秒延时起爆模型Fig.2 Two-segment millisecond delay initiation models
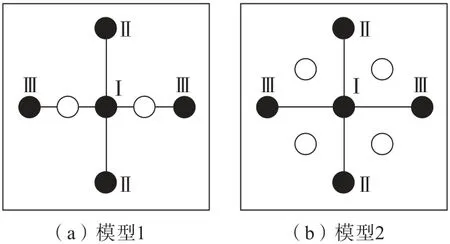
图3 三段毫秒延时起爆模型Fig.3 Three-segment millisecond delay initiation models
2.3 材料参数及本构方程
模型采用多物质流固耦合(ALE)算法,其中将炸药和空气部分作为流体处理,岩石部分作为固体处理。相互作用采用*constrained_lagrange_in_solid[13]关键字来设定。岩石本构方程选择*MAT_PLASTIC_KINEMATIC模型,该模型可描述各向同性硬化和随动硬化塑性模型,还可以考虑应变率的影响,适用于梁、壳和实体单元,计算效率很高。岩石材料的具体参数取值见表2。炸药计算模型采用*MAT_HIGH_EXPLOSIVE_BURN,为了保证炸药顺利起爆设定炸药的状态方程为*EOS_JWL,炸药材料和状态方程的具体参数取值见表3。空气材料选择*MAT_NULL,其状态方程*EOS_LINEAR_POLYNOMIAL[14-15],空气材料的具体参数取值见表4。

表2 砂岩基本物理力学参数Table 2 Basic physical and mechanical parameters of sandstone
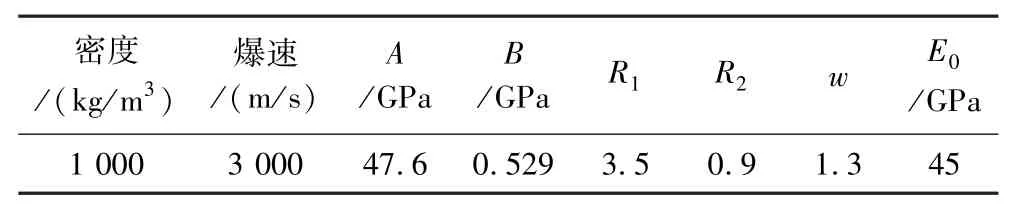
表3 JWL状态方程参数Table 3 Parameters of JWL state equation

表4 空气材料和状态方程参数Table 4 Air material and equation of state parameters
2.4 数值计算模型可靠性验证
数值模型建立后需验证其可靠性,确保模拟结果能够有效反映基本爆破机理[16]。在爆破孔和空孔连接方向均匀地选择7个测点,得出的振动速度与萨道夫斯基公式理论解对比如图4所示。
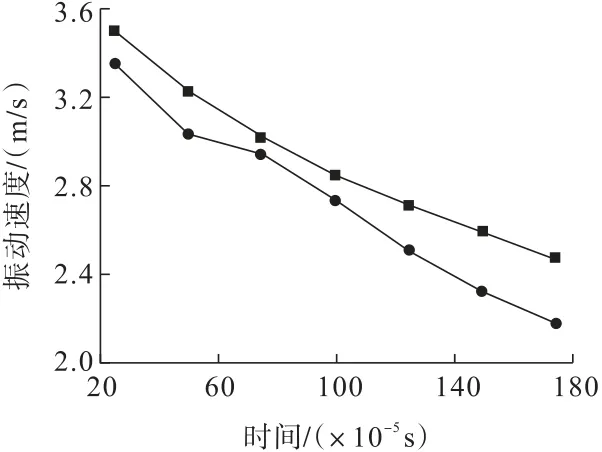
图4 振动速度数据对比曲线Fig.4 Comparison curves of vibration velocity data
由图4可知:数值计算解和理论公式得出的结果变化趋势基本一致,后者总体上小于前者,原因在于实际工程中岩层中存在多种裂隙和不同岩层等多种因素的影响,这些因素能够有效降低振动效应,起到了类似减震沟[17-18]的减振效果,但总体变化趋势一致,且结果相差不大,因此使用该模型模拟爆破具有一定的可靠性。
3 数值模拟计算结果分析
3.1 不同间距对比
依据含空孔掏槽爆破岩石的开裂机理,结合数值模拟计算,从中能够得出同类型布孔方式条件下,不同间距的对比方式。本研究主要分析空孔被填满情况、爆破孔和空孔连接处测点的有效应力和最终裂隙扩展情况。由于篇幅有限,故以同时起爆模型1(图1(a))为例,分析间距判别方法。
3.1.1 空孔被挤压程度
同时起爆模型1各间距空孔处的应力分布特征如图5所示。
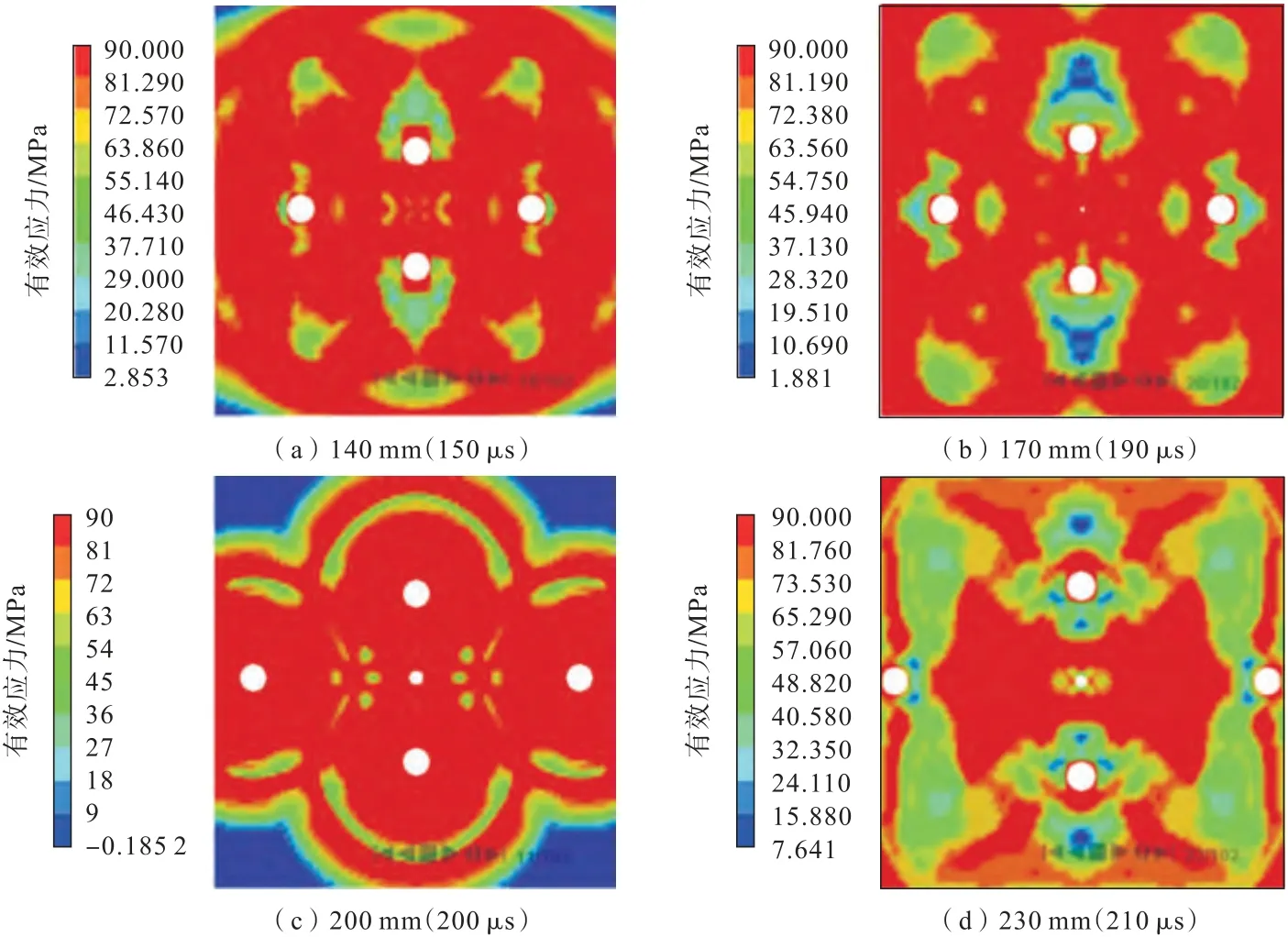
图5 同时起爆模型1各间距空孔处应力分布Fig.5 Stress distribution at each spacing empty hole in No.1 simultaneously detonate model
由图5可知:在140 mm间距中,空孔在150 μs时被碎石填满,空孔被完全挤压;对比170 mm间距的空孔,虽然所剩空孔的体积很小,但是满足了补偿空间理论,且所用时间也较长,说明相比于140 mm间距,170 mm间距优势更为明显,但是为了防止后续爆生气体的二次气楔作用所产生的碎岩将剩余的空间填满,因此有必要对此间距做进一步分析;200 mm间距的空孔剩余体积较大,约占原来的1/4,剩余的体积较多,且对比170 mm间距情况所用时间仅仅推迟了10 μs,虽然保证了空间被完全占据,但是所剩空间过大;由于230 mm间距所示的空间甚至小于200 mm间距的空间,故直接排除。由此可以推出较为优势的间距为170~200 mm,并排除140 mm间距的情况,这与理论公式所得数据相近。
3.1.2 爆破孔和空孔连接处测点的有效应力
在模型爆破孔和空孔连接方向均匀布置7个测点,得到有效应力的时程曲线。将各个曲线的稳定有效应力进行统计,而后筛除小于砂岩抗拉强度的应力值,取7个应力值的平均值作为该间距的有效应力,再对比4种间距的有效应力,从中取最小值即可作为较优应力,具体数据曲线如图6所示。
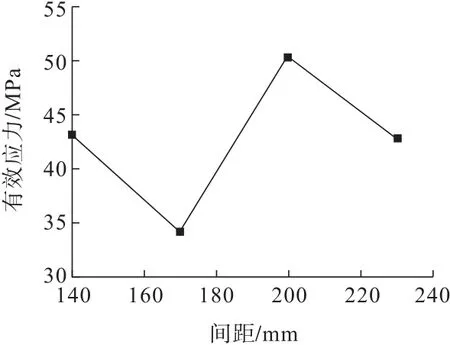
图6 同时起爆模型1有效应力随间距变化曲线Fig.6 Variation curve of effective stress with distance for No.1 simultaneous detonation model
由图6可知:有效应力随着间距的变化先下降后增长再下降,变化起伏较大;在170 mm处达到最低值,该处有效应力大于砂岩的抗拉强度且又处于曲线的最低值,因此符合最适宜条件。
3.1.3 裂隙扩展情况
1 000 μs时,同时起爆模型1的最终裂隙分布特征如图7所示。
由图7可知:所有情形下的裂隙均延伸出了边界,最终所有孔均贯通。其中200 mm间距的裂隙范围明显少于其他情况,230 mm间距的裂隙在空孔周围没有很好地粉碎,裂隙较少。而140 mm间距和170 mm间距两种情况均在空孔处具有较好的粉碎效果,但由于排除了140 mm间距的情况,所以170 mm间距的情况较好。
3.1.4 最适间距
综合3种判断方法,只有170 mm间距的情况最为突出,因此在此种布孔方式下,170 mm为最适宜间距。
最终通过32组应力波分析和32组裂隙扩展情况分析,得出各模型的最适宜间距取值见表5。
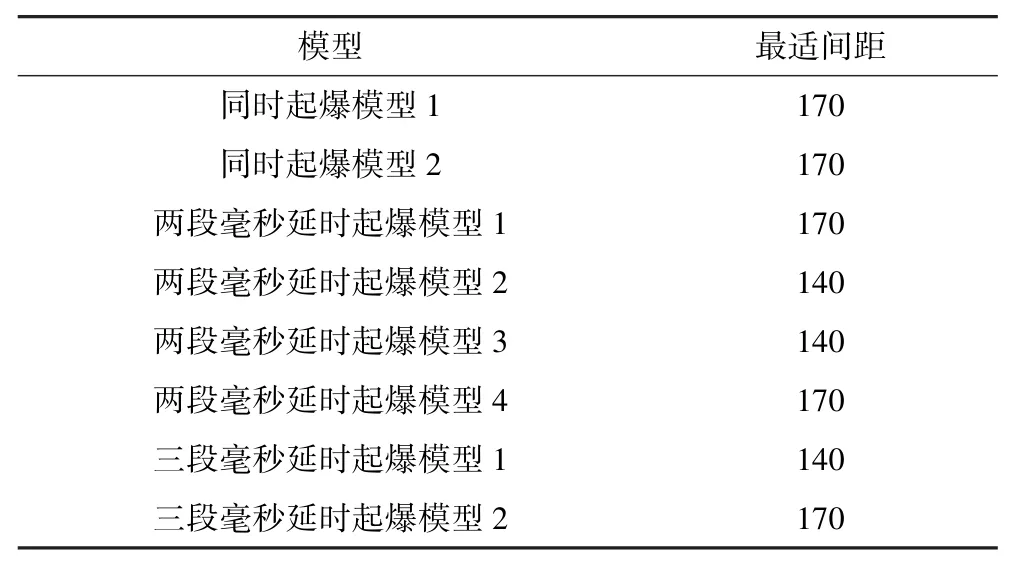
表5 各模型最适宜间距Table 5 Optimal spacing of each model mm
3.2 不同布孔方式对比
由3.1节得出各种布孔方式的最适宜间距后,通过对比相同起爆段数的模型,能够得出最优布孔方式,本研究以两段毫秒延时起爆模型(图2)为例进行分析。
3.2.1 爆破孔和空孔连接处测点的有效应力
两段毫秒延时模型间距的有效应力随间距的变化曲线如图8所示。
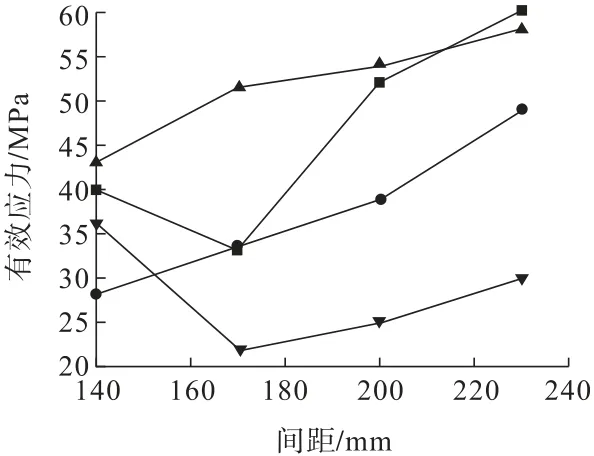
图8 两段毫秒延时起爆各模型有效应力随间距变化曲线Fig.8 Variation curves of effective stress with spacing of each model of two-segment millisecond delay initiation
由图8可知:各模型的最适宜孔间距均选择为曲线中的最小值(表5),并且均符合在大于砂岩抗拉强度的基础上取最小值的条件。因此,本研究在此基础上直接对比各模型最适宜孔间距的有效应力最小值,发现模型4中170 mm间距为最适宜孔间距,并且该模型的有效应力整体较小。
3.2.2 裂隙扩展情况
1 000 μs时,两段毫秒延时爆破模型中的最适宜间距裂隙扩展情况如图9所示。
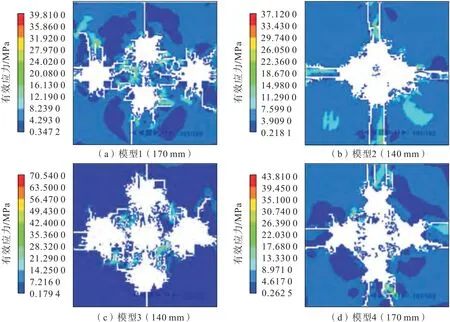
图9 两段毫秒延时起爆各最适宜间距最终裂隙分布Fig.9 Distribution of the final cracks at each optimal distance between two-segment millisecond delay initiations
由图9可知:模型2的裂隙开裂范围最小,模型3最大,模型1开裂范围呈长方形分布,模型2开裂范围集中在空孔处,模型3和模型4开裂范围呈菱形分布。岩石碎裂程度方面,模型3和模型4岩石已经粉碎,而模型1中存在较大的岩层,模型2岩石粉碎程度太高,范围过小,说明用于粉碎空孔附近处岩石的能量过剩,能量分布不均匀。因此综合分析,模型3和模型4较优,再结合有效应力分析,模型4最优。
3.2.3 最优布孔方式
依据上述分析方法得出各模型的最优布孔方式为同时起爆模型1(图1(a))、两段毫秒延时起爆模型4(图2(d))和三段毫秒延时起爆模型2(图3(b))。
3.3 不同起爆顺序对比
按照3.2节得出各种起爆方式的最优布孔方式后,通过对比不同起爆时间的模型,能够得出最优起爆方式。
3.3.1 爆破孔和空孔连接处测点的有效应力
3种最优布孔方式的有效应力随间距的变化曲线如图10所示。
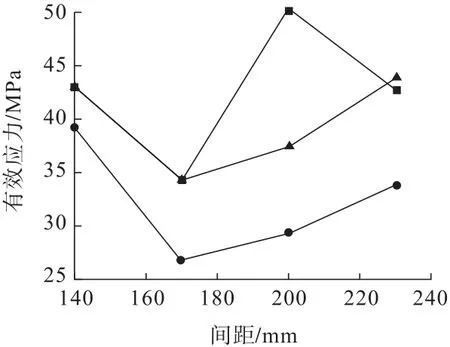
图10 不同起爆顺序下各模型有效应力随间距变化曲线Fig.10 Effective stress variation curves of each model with spacing under different initiation sequences
由图10可知:模型4和模型2的变化趋势均为先下降后上升,模型1的变化较为波动,呈先下降后上升再下降的变化规律。模型1有效应力整体较大,因此直接排除;模型4的有效应力均小于模型2,因此两段毫秒延时起爆模型4较优。
3.3.2 裂隙扩展情况
1 000 μs时,170 mm孔间距下同时起爆模型1、两段毫秒延时起爆模型4和三段毫秒延时起爆模型2的裂隙扩展情况如图11所示。

图11 最优模型间距裂隙分布Fig.11 Distribution of cracks with optimal model spacing
由图11可知:模型4和模型2在空孔附近处裂隙较为密集,开裂情况较好,模型1空孔附近裂隙相对较少且不够密集。在外部相邻爆破孔开裂情况中,模型1开裂较差,甚至部分没有开裂,而模型4和模型2虽然裂隙不多也并未向外扩展,但是在该处形成了一定的破碎,裂隙呈菱形分布,通过分析可以排除同时起爆模型1。模型4和模型2的内部裂隙开裂都较为均匀,对于两者需进一步开展适宜性分析,但两者均采用相同的布孔方式,故可以认为该布孔方式最优。
3.3.3 最优模型
由上述分析可知:两段毫秒延时起爆模型4和三段毫秒延时起爆模型2为较优解,两者为同种布孔方式、不同起爆方式,再结合3.3.1节分析可知,模型4的有效应力较优,因此得出最优起爆顺序为两段毫秒延时起爆,最优布孔方式为两段毫秒延时起爆模型4,最适间距为170 mm。该结论与第1节理论公式推导出的结果相差不大,在工程实践中可以适当调整孔间距。
4 工程实例分析
4.1 爆破参数设计
依据2.1节的工程背景,新方案以两段毫秒延时起爆为最优起爆顺序,两段毫秒延时起爆模型4(图2(d))为最优布孔方式,170 mm为最适宜间距,(其他爆破参数与旧方案相同);旧方案的掏槽方式为两段毫秒延时起爆模型2(图2(b))。新方案炮孔布置如图12所示,工作面各类炮孔参数取值见表6。
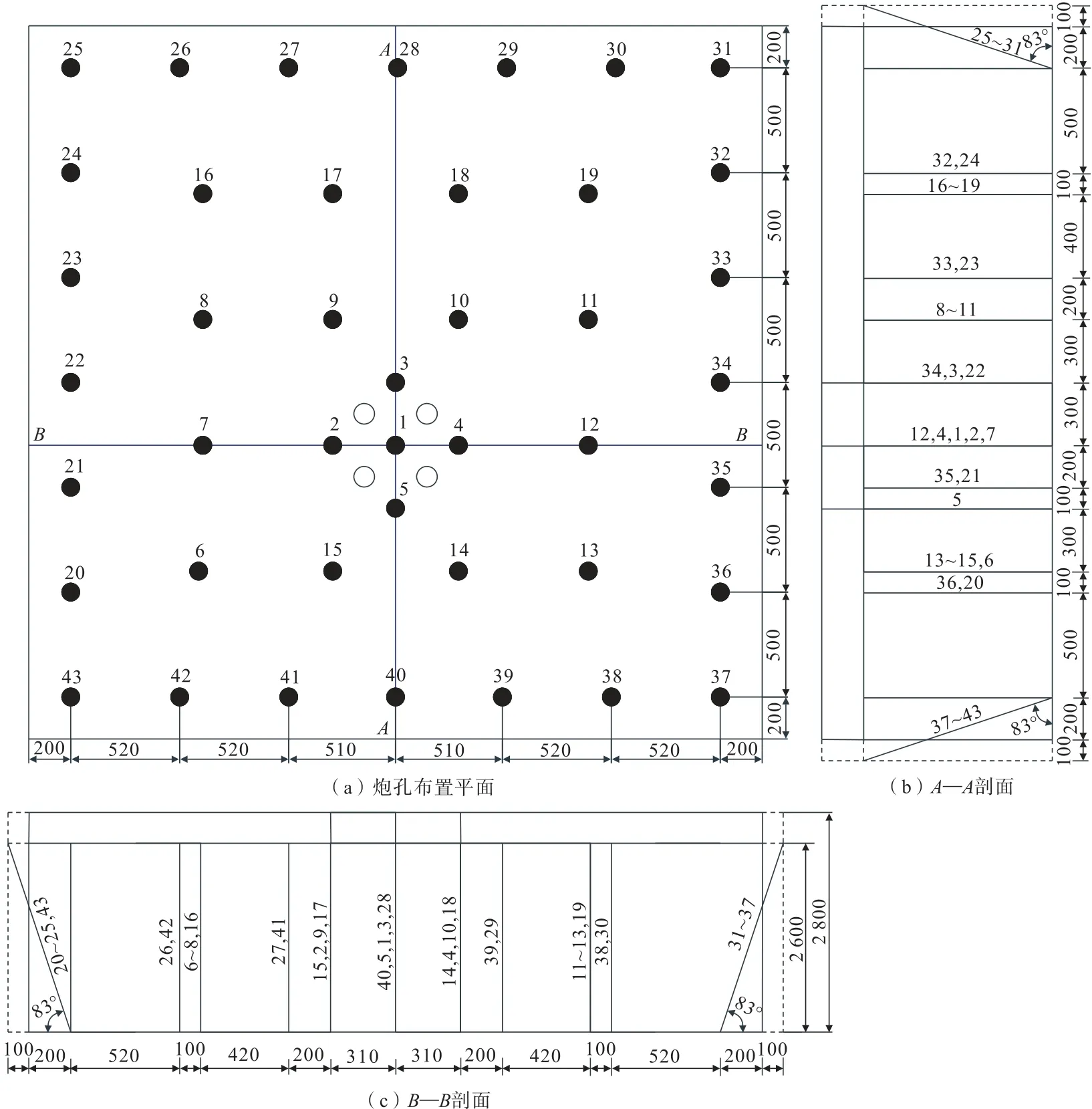
图12 炮孔布置示意(单位:mm)Fig.12 Schematic of the layout of blasting holes

表6 巷道爆破参数Table 6 Blasting parameters of roadway
4.2 爆破效果分析
通过对比新旧方案的爆破效果,进一步探讨新方案能否提高岩巷掘进效率,现场实践效果如图13至图15所示。

图13 现场炮孔布置Fig.13 On-site blasting holes layout

图14 巷道掘进效果Fig.14 Excavation effect of roadway

图15 新旧方案爆破效果对比Fig.15 Comparison of the blasting effects of the new and original schemes
由图13和图14可知:现场根据理论模型和数值模型设置了相同的布孔方式和间距,掘进深度也符合预期,巷道成型完整,没有出现超欠挖现象。由图15可知:新方案的矸石更小,破碎更完全,旧方案矸石较大,但两者的碎石大小均在可接受范围内。
新旧方案的巷道主要爆破条件和技术经济指标对比见表7。

表7 新旧方案主要爆破条件和技术经济指标Table 7 Main blasting conditions and technical and economic indicators of the new and original schemes
结合表7分析可知:在施工措施和岩层相同的条件下,通过5次爆破掘进试验,新方案与旧方案相比,平均爆破进尺增加了0.17 m,炮孔利用率提高了5%,槽腔体积增大了1.35 m3,单循环出岩量增加0.5 m3,可见新方案能够有效提高岩巷掘进效率。在爆破耗材方面,掏槽药量降低0.7 kg,每循环消耗炸药量降低2.66 kg,炸药单耗降低0.11 kg/m3,每米巷道消耗雷管降低1.7个,反映出新方案不仅提高了掘进效率,还大大降低了爆破耗材,提高了经济效益。两种方案中岩石爆破均比较充分,工作面岩石碎块均匀,大块率较低。多次爆破中除了个别出现少量大块外,岩石均比较集中,大小处于较易抛掷的范围,大幅降低了人工清矸的工作量。
4.3 峰值振动速度对比
在距离工作面300 m处设立振速测试仪,并将其安置在顶部锚网处,主要监测巷道顶部的合速度峰值振动速度,具体数据见表8。
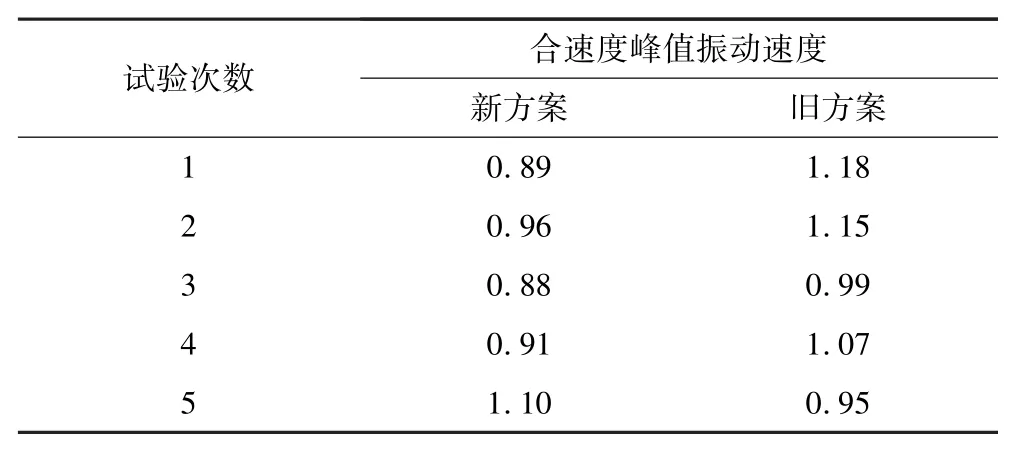
表8 合速度峰值振动速度监测结果Table 8 Monitoring results of combined speed peak vibration speed cm/s
由表8可知:新方案的合速度峰值振动速度普遍小于旧方案,综合5次试验结果,取其平均值发现新方案的振动速度更小,对巷道的整体稳定影响更小。新方案的合速度峰值振速比旧方案平均减少了0.12 cm/s,可见新方案不仅能够提高掘进效率和经济效益,而且能够减少振动带来的影响,保障了巷道掘进安全施工。
5 结 论
(1)结合补偿空间理论和应力集中效应,对裂隙半径经验公式进行改进,限制了半径的最小值,并得出理论最适宜孔间距为179 mm;数值计算发现最适宜孔间距出现在有效应力最低处,结合数值计算和现场数据,验证了最适宜孔间距取值的可行性和可靠性。
(2)理论分析结果、数值模拟结论和现场爆破效果在最适宜孔间距方面表现出一致性,综合分析发现,最优起爆顺序为两段毫秒延时起爆,最优布孔方式为两段毫秒延时模型4,最适孔间距为170 mm,数值计算结果、实际工程结论与理论结果差别较小,在实际工程中可适当小范围调整孔间距。
(3)结合山西天地王坡煤业有限公司3206高抽巷现场爆破数据,发现新方案相比于旧方案爆破进尺增加0.17 m,炮孔利用率提高5%,每循环消耗炸药量降低2.66 kg,每米巷道消耗雷管降低1.7个,振动速度平均降低0.12 cm/s,提高了经济效益和巷道掘进效率,减少了振动带来的潜在危害。
(4)本研究仅在数值模拟软件中模拟了多种参数的变化,未在实际工程中进行详细的参数变化分析,下一步可在工程施工中改变相关参数,进一步研究参数变化对爆破效果的影响。

