基于支持向量机的瓦斯隧道揭煤施工突出危险性预测
*苗德华 刘锟林
(1.湖南科技大学 资源环境与安全工程学院 湖南 411201 2.浙江交工集团股份有限公司西南分公司 贵州 550001)
随着我国经济的快速发展,对交通运输的能力提出了更高的需求,其中陆路运输承担着主要运输职能,而隧道工程是陆路运输中必不可少的环节,是我国实现交通强国的重要组成[1]。鉴于作业环境的受限性与地质条件的复杂性,隧道施工事故频繁发生,给隧道施工安全带来了巨大挑战[2]。为了能够预测瓦斯隧道揭煤施工的突出危险性、降低施工风险和提高施工效率,有必要开展瓦斯隧道事故统计分析以及建立揭煤突出危险性预测模型。
现已有大量学者对于隧道施工风险评价预测展开了研究。隧道瓦斯事故影响因素评价分析的主要研究方法有模糊-熵权理论、模糊综合评价法、属性数学理论法、支持向量机和径向基神经网络等。但支持向量机应用于瓦斯隧道揭煤施工突出危险性预测的研究较少,且没有考虑到隧道施工与煤矿施工影响因子的差异。
本文通过统计瓦斯隧道揭煤施工事故来归纳分析影响揭煤施工突出危险性的因素,进而研究瓦斯隧道揭煤施工突出危险性的支持向量机预测模型。
1.事故统计及影响因素选取
本文通过查阅国家安全生产监督管理总局、新闻来搜集2001—2021年间发生的瓦斯隧道揭煤施工事故。
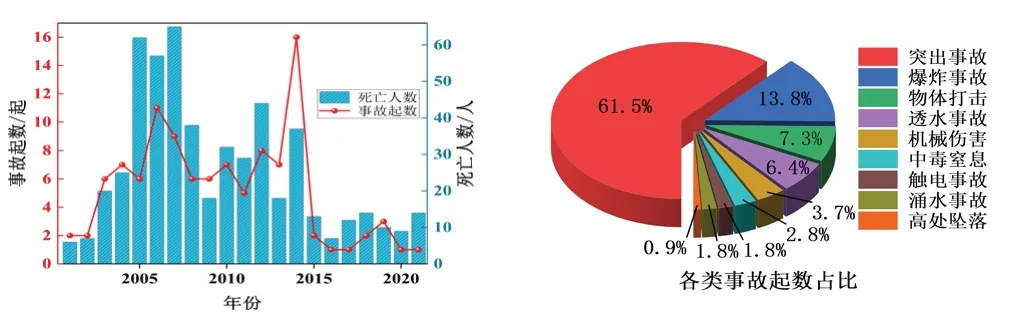
图1 事故统计及类型占比
如图1所示,共统计到事故109起,死亡537人,其中2001年死亡6人,2007年死亡人数达65人,分别是死亡人数最少和最多的年份。2006年和2014年是事故发生数量较高的年份,分别为11次和16次。2016年、2017年、2020年及2021年事故发生数量最低,均为1次;其中死亡人数与事故次数总体上呈现相关性,其趋势虽然有上下起伏,但总体上呈下降趋势;在隧道揭煤事故中隧道穿越瓦斯煤层的坍塌、冒顶、倾出及压出等事故可以统称为突出事故。因此本文将隧道揭煤事故按照相关资料及隧道事故特征分为九类,具体见图1。其中突出事故在众多事故类型中是发生次数及致死人数最多的,共发生67次,占总体的61.5%,累计死亡308人,占总体的57.4%。因为突出事故是由多种因素综合影响的,其中地质因素和施工因素是导致突出事故的众多因素中的重点。揭煤施工突出危险是地应力、瓦斯和煤层物理力学特性等多因素综合作用下的气固耦合介质的力学过程[3],所以本文根据《防治煤与瓦斯突出细则》选取影响因素X1~X7,经查阅文献考虑瓦斯隧道与煤矿差异提出影响因素X8和X9,共9个影响因素用来作为预测指标,如表1所示。
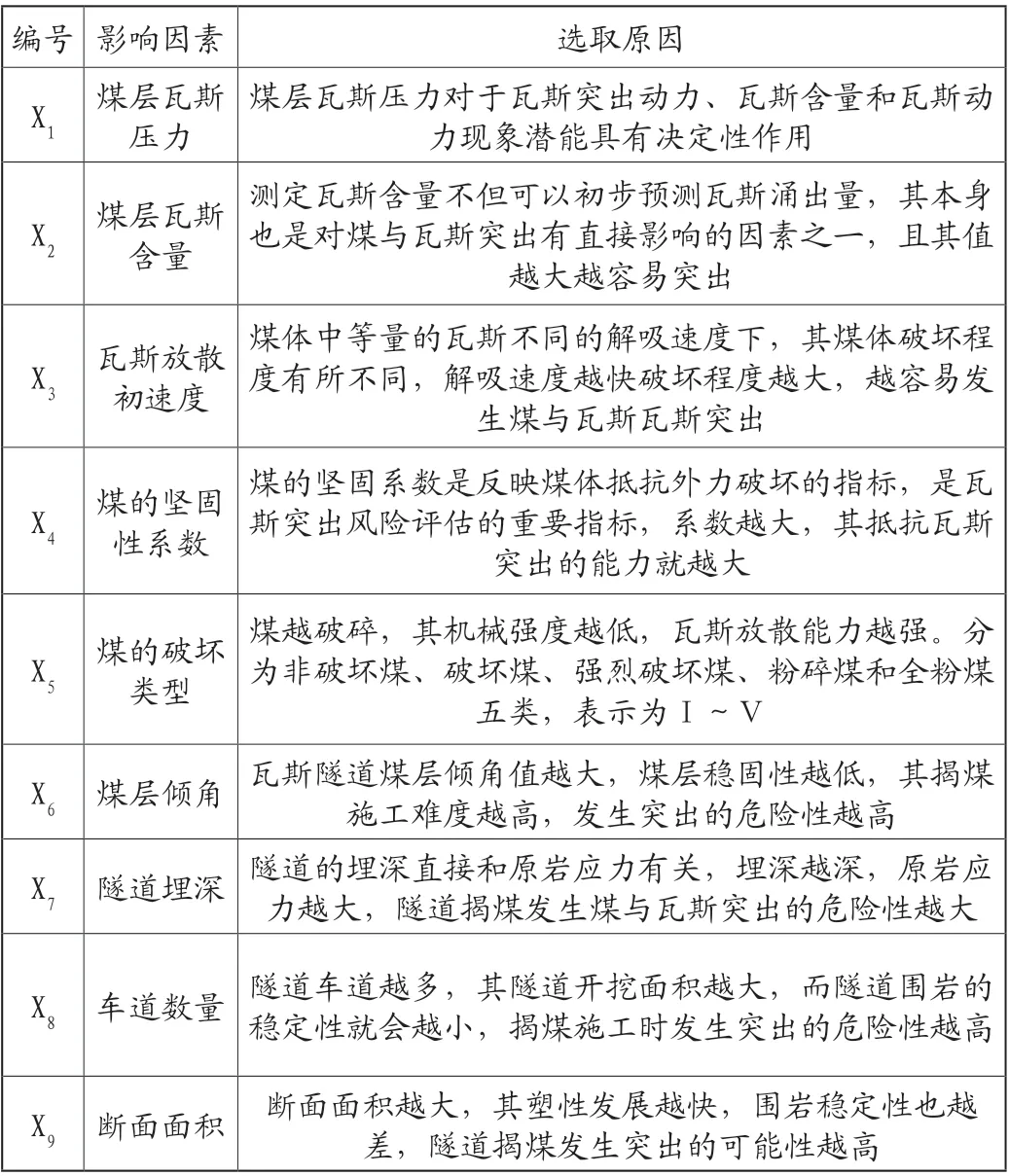
表1 揭煤施工突出危险影响因素及选取原因
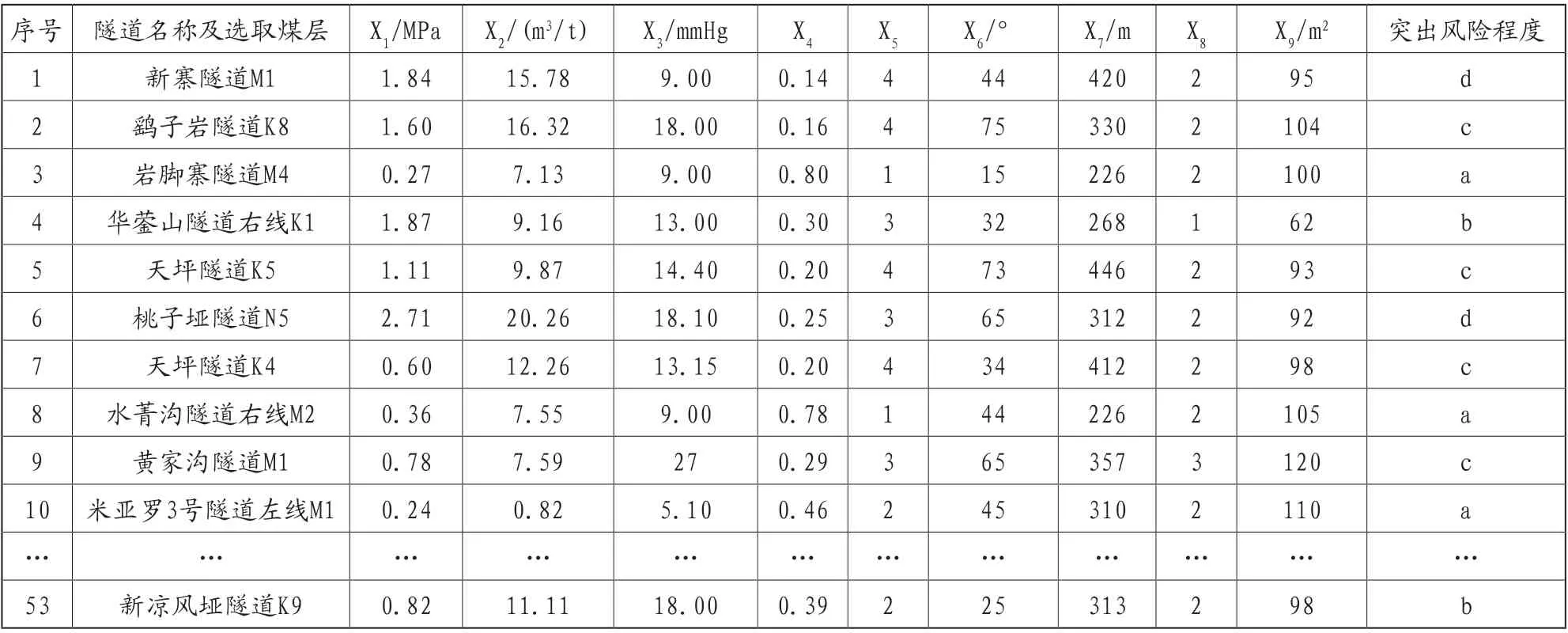
表2 支持向量机训练及验证样本
2.支持向量机的训练及预测
(1)样本选择
以瓦斯隧道揭煤施工突出危险性为研究对象,通过查阅瓦斯隧道文献共获得53个已知突出风险程度的样本,来对预测模型进行训练及验证,如表2所示。
在表2中,煤的破坏类型Ⅰ~Ⅴ用数值1~5来代表;隧道揭煤突出风险程度分为4类,即无突出风险(a,突出量达到0)、轻度突出风险(b,突出量达到0~50t)、中度突出风险(c,突出量达到50~100t)和严重突出风险(d,突出量大于100t)。
(2)训练及验证
将表2中样本数据导入MATLAB中,采用10折交叉验证法进行处理,其中65%作为训练集、35%作为验证集,其中X1~X9作为输入,突出危险程度作为输出,运用支持向量机来进行训练、验证及预测。
将训练样本分别在线性核函数和高斯核函数下进行训练,可以得到以下混淆矩阵及其AUC值,AUC值为积分求得ROC曲线面积,其值一般在0.5~1之间,越靠近1表示越接近理想分类模型。
图2、图3为两种核函数训练集和验证集的混淆矩阵;图中TPR为真正率,FNR为假负率,PPV为正预测值,FDR为假发现率。
其中线性核函数AUC值为:训练集a类为1.00,b类为0.93,c类为0.96,d类为1.00;验证集a类为1.00,b类为0.97,c类为0.99,d类为1.00。高斯核函数AUC值为:训练集a类为0.98,b类为0.91,c类为0.97,d类为1.00;验证集a类为1.00,b类为1.00,c类为1.00,d类为1.00。
最终得出两种核函数的综合准确率,线性核函数为88.2%,高斯核函数为94.1%。
从AUC值方面可以看出:①训练中,线性核函数在a类和b类的AUC值比高斯核函数高,c类的AUC值不如高斯核函数。②验证中线性核函数在b类和c类中AUC值低于高斯核函数。
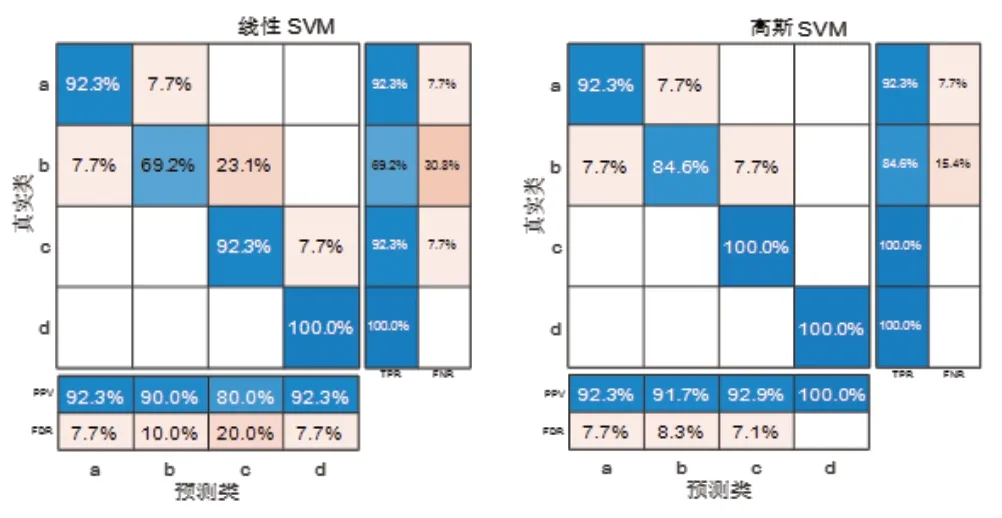
图2 线性混淆矩阵
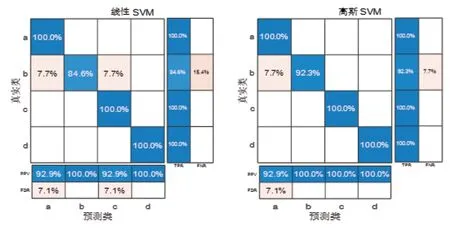
图3 验证混淆矩阵
从图2~图3可以看出:①在训练过程中,线性核函数错误识别的情况有:a类识别为b类;b类识别为a类和c类;c类识别为d类。高斯核函数识别错误的情况有:a类识别为b类;b类识别为a类和c类;②在验证时,线性核函数预测错误的情况有:b类预测为a类和c类。高斯核函数预测错误的情况有:b类预测为a类。③高斯核函数在指标TPR、FNR、PPV和FDR均比线性核函数的表现要好。
综上所述,在训练过程中线性核函数准确度不如高斯核函数,但在AUC值方面综合好于高斯核函数;在验证过程中高斯核函数均好于线性核函数。通过验证集混淆矩阵可以看出两种核函数均在b类预测中有所误差,而验证集AUC值可以看出线性核函数在b类、c类的AUC值比高斯核函数低,所以后续实际应用预测时可能会在b类的突出风险预测出现误差,且线性核函数出现误差的可能性比高斯核函数要高。
(3)工程验证
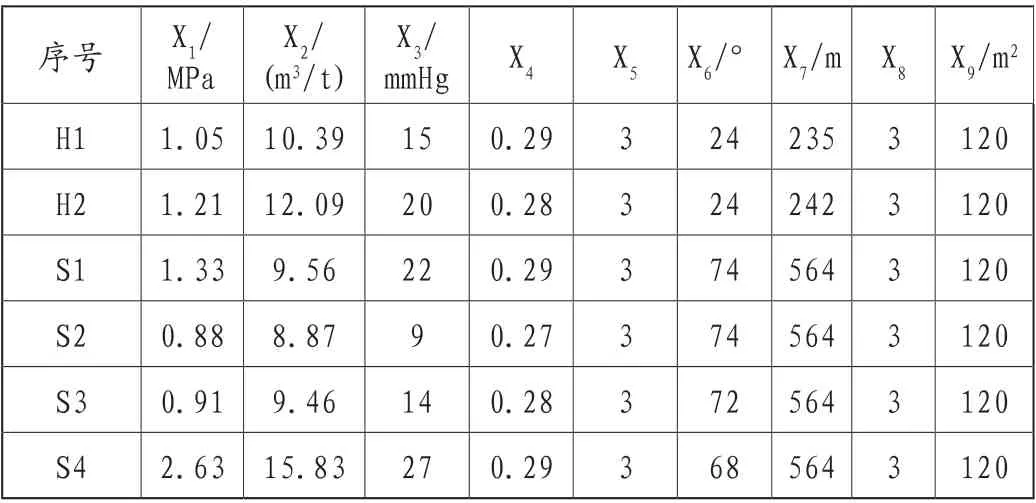
表3 预测样本
将已成功贯通的黄家沟隧道、松坎隧道的煤层揭煤施工前数据代入模型进行验证。样本来自于黄家沟隧道ZK16+016埋深230~250m处所经过的两个煤层中,分别取样并命名为H1、H2;以及松坎隧道左线ZK6+540里程掌子面前方80m范围的四层煤层中,分别取样并命名为S1、S2、S3、S4。因此从工程项目中共选取6个样本来进行预测验证,见表3。
支持向量机对样本进行预测的突出危险程度及施工前安全评价公司评审突出危险程度见表4。
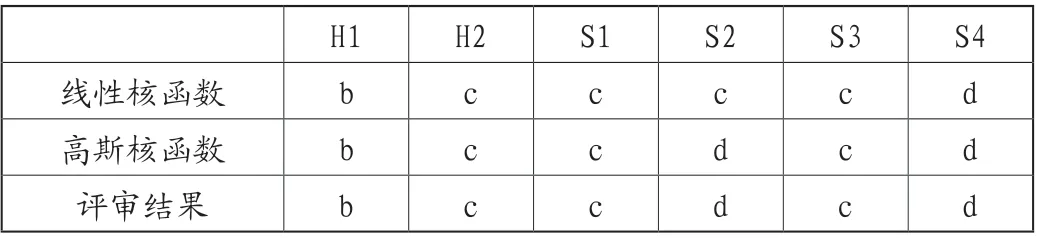
表4 预测结果及评审结果
由表4可以看出线性核函数支持向量机错误预测了S2的危险程度,综合可知H1为轻度突出危险性,H2、S1、S3为中度突出危险性,S2、S4为严重突出危险性,因此应着重预防H2、S1、S2、S3和S4揭煤施工时发生事故,但实际施工过程中虽然进行了预防防范,却仍有煤层揭煤施工时发生相关事故。
综上所述,线性核函数支持向量机错误预测了S2,高斯核函数支持向量机准确率较高,说明在此次工程项目预测中高斯核函数支持向量机模型更适用。而在可能出现预测错误的方面可以从AUC值和混淆矩阵上得知。
3.结论
(1)本文统计了2001—2021年我国瓦斯隧道揭煤施工事故,将事故分为9类,而主要类型为突出事故,并总结归纳了影响揭煤施工突出危险性的9个因素。
(2)通过支持向量机的训练及验证,得出线性核函数综合准确度为88.2%,高斯核函数的综合准确率为94.1%,并对工程项目中选取的样本进行预测验证。
(3)通过高斯核函数支持向量机预测结果可知,工程案例揭煤施工段若不做合理的揭煤防突措施,将会发生不同程度突出事故的危险,这与实际施工过程相符,可为同类型的瓦斯隧道揭煤施工突出危险性预测提供依据。

