提升风电调频性能的源储协同控制策略

姚路锦， 王 玮， 蔡 玮， 刘吉臻

(华北电力大学 新能源电力系统国家重点实验室，北京 102206)

在全球碳中和及能源转型的背景下，我国持续出台相关战略及政策来支持清洁能源发展，截至2022年3月底，我国风电累计装机3.37亿kW[1]。清洁能源装机容量和发电量不断增加，其出力不确定性加重了电网“源荷”两侧的功率不平衡问题，严重威胁电网频率安全[2-4]。因此，对于高风电渗透率下逐渐形成的低惯量电力系统[5]，其频率稳定性仅靠传统同步发电机组支撑调频明显不足，有必要引入其他能源的辅助调频[6-8]。

在传统机组存在发展局限性的情况下，电池储能系统(Battery Energy Storage System，BESS)凭借其可提前备用、响应快速、跟踪精确和双向调节等优点成为辅助调频的优质能源[9]。Arrigo等[10]通过可变下垂控制策略来保持电池状态，同时研究了BESS对一次调频电网暂态响应的影响。邓霞等[11]考虑不同频率区间内电网对调频的需求，提出了包括虚拟下垂、虚拟惯性及负惯性综合控制的电池自适应控制方法，提高了电网频率稳定性。Marzebali等[12]通过加入燃料电池来缓解电池储能的调频压力，实现快速补偿功率。面临电网复杂庞大的调频压力，单一地依靠储能进行辅助调频，需要配备足够容量的电池储能设备，但BESS的前期投入以及维护成本较高，难以保障调频收益。

近年来，相关专家学者对如何将风电纳入电网调频体系进行了研究[13]，风电机组和储能系统协同参与辅助调频成为较优选择。Bao 等[14]提出一种分层惯量控制策略来协同控制风电机组和BESS，以成本最低为目标来确定风储的出力参考；彭勃等[15]根据风机特性将风速分区，并针对各区域的特点设计了相应的风储运行策略，有效提升了系统惯性和短期频率响应能力；杨伟峰等[16]提出一种风储双层频率响应控制策略，满足调频需求的同时降低了调频成本和风机的疲劳载荷[17-18]；曲彤等[19]通过设计分频系统确定风火储的有功出力，提高了系统调频速度和调频质量。然而，同时考虑传统机组、风电场和储能场站的场级协同优化来提升各场站的灵活性及调频性能的相关报道还较少。

针对上述问题，笔者从场级调度出发提出一种基于自适应模型预测控制(Adaptive Model Predictive Control，AMPC)的源储协同调频策略，通过考虑储能调频系数的自适应变化和目标函数的优化求解，灵活调整各场站的调频出力，同时提升风电调频性能。

1 风储一次调频模型

储能和风电场可以通过虚拟下垂和虚拟惯性控制[11]来参与调频。下垂控制能大幅缩减频率偏差，惯性控制则对频率偏差变化率具有较好的抑制作用[20]。结合二者的优势构成风储协同系统辅助火电机组调频，可以充分发挥风电场及储能的调频优势，在保证快速性的同时优化调频效果。当系统频率下跌时，风电机组通过增发功率协同储能辅助火电机组提供功率支撑；当系统频率上升时，风电机组通过减载或同火电机组一起给储能装置充能，抑制频率波动的同时恢复储能的荷电状态(SOC)。

1.1 频率变化率

频率变化率[21](ROCOF)是电力系统调频过程中的重要参数，与调频系统中各机组出力和频率变化情况密切相关。利用它来辨别当前时刻的调频状态，加入合适的下垂及惯性控制量，可以实现对风、储系统调频出力的控制。对于同时存在风、火、储的一次调频系统，其动态响应等效状态方程为：

(1)

式中：M*为系统等效惯性时间常数，M*=M(1-p)[22]，其中M为电网等效惯性时间常数，p为风电渗透率；D为等效负荷阻尼系数；f为电网频率;Δf为频率变化量；TJ、Kf分别为风电场的等效惯性时间常数和有功一次调频系数；KE,I、KE,D分别为储能系统的虚拟惯性和下垂控制系数，其中I、D分别表示惯性及下垂变量；ΔPG、ΔPWF、ΔPE分别为火电机组、风电场和储能系统的功率变化量；PL为扰动负荷功率；ΔPUnb为功率不平衡量。

对式(1)进行线性化，并由初值定理可得系统在tn时刻的初始ROCOF，即F(tn)为：

(2)

式中：t为时间。

1.2 风电场调频模型

根据国标[23]规定，风电场应该具有快速控制自身有功功率，提供惯量响应和一次调频的功能，并可以根据电力系统运行的实际需要启用与停用惯量响应和一次调频功能。则风电场基于ROCOF提供的调频出力为：

ΔPWF(s)=ΔPWF,I(s)+ΔPWF,D(s)

(3)

其中，风电场提供的惯量响应为:

(4)

一次调频响应为：

(5)

式中：PWF为风电场实时有功功率；PWF,N为风电场额定功率；fN为电力系统额定频率;s为拉普拉斯算子。

1.3 储能系统调频模型

考虑BESS的调频特性，储能系统基于ROCOF提供的调频出力为：

ΔPE(s)=ΔPE,I(s)+ΔPE,D(s)

(6)

其中，电池储能系统提供的虚拟惯性控制量为：

(7)

虚拟下垂控制量为：

ΔPE,D(s)=-KE,DGE(s)Δf/fN

(8)

式中：GE(s)为电池储能系统等效传递函数。

2 基于AMPC的源储协同控制策略

2.1 储能系统自适应调频控制

BESS参与调频时需要持续出力，为保证储能的SOC在规定的范围内，避免出现过充或过放，应对电池的SOC变化进行实时监测与控制。此外，调频动作结束后，在不越过电网一次调频死区的情况下，可对SOC进行自恢复调节，尽量将电池SOC调整到最佳水平，为后续调频动作做好准备。

2.1.1 基于SOC反馈的储能调频系数

由于通过BESS统一实现的虚拟下垂和惯性控制，本文设置为相同的调频系数KE，其在充放电过程中分别对应放电系数Kd和充电系数Kch。通过引入Logistic回归函数[24]，以SOC的值S为自变量,储能功率调节系数Kd和Kch为因变量,功率因子K0和系数n为参变量建立KE-S曲线模型，在满足系统调频需求的前提下自适应地根据调频工况对储能充放电功率进行调节。

(9)

(10)

式中：KE,max为储能系统调频系数最大值。

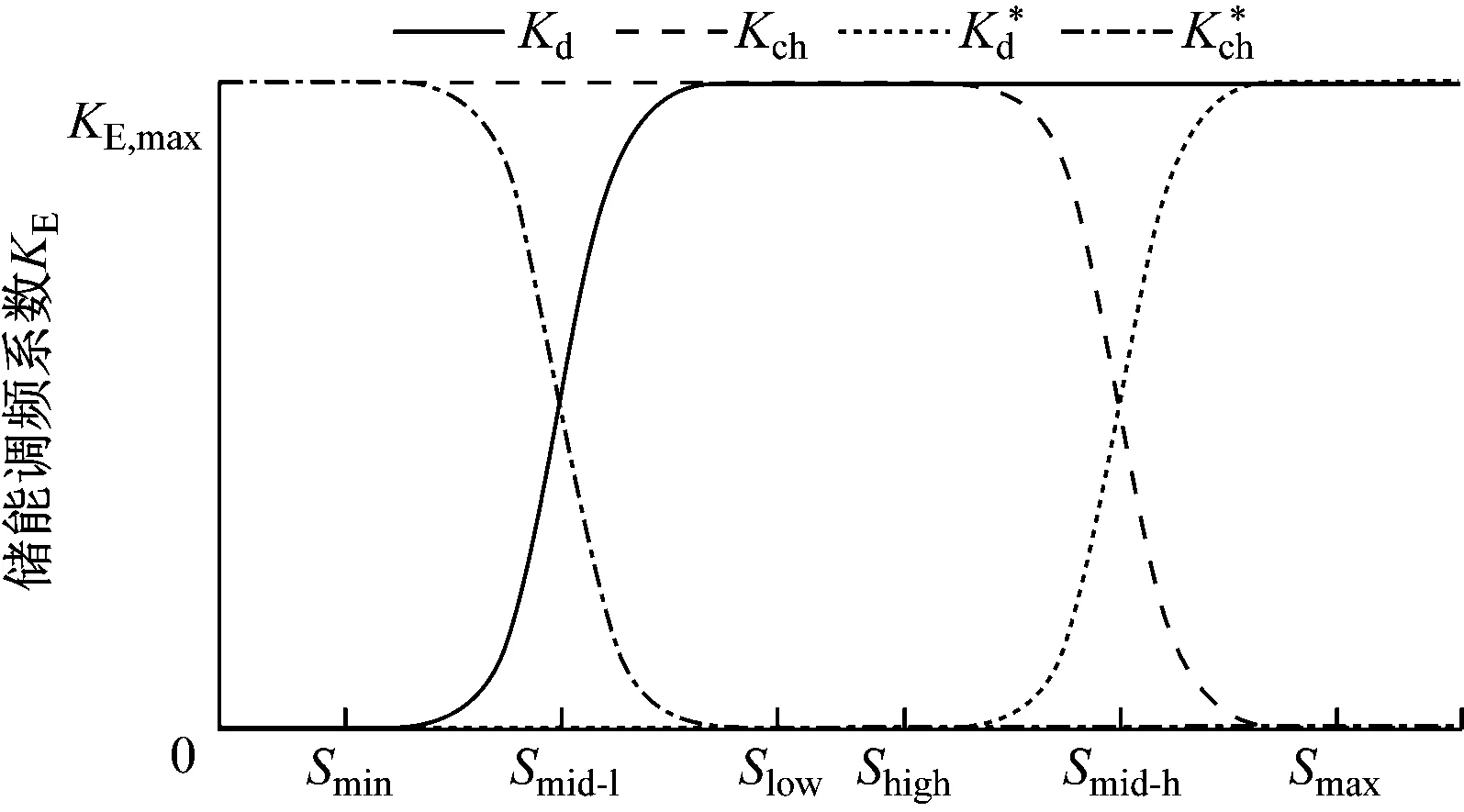
图1 储能系统调频系数及自恢复调节系数

2.1.2 SOC自恢复调节系数

(11)

(12)

由此计算储能SOC恢复出力ΔPE,Rec(s)为：

(13)

则储能SOC的自恢复量ΔS*(s)为：

(14)

式中：T为采样周期；η为储能系统充放电效率；EN为储能系统额定容量。

基于SOC状态反馈的储能自适应调频控制框图如图2所示。

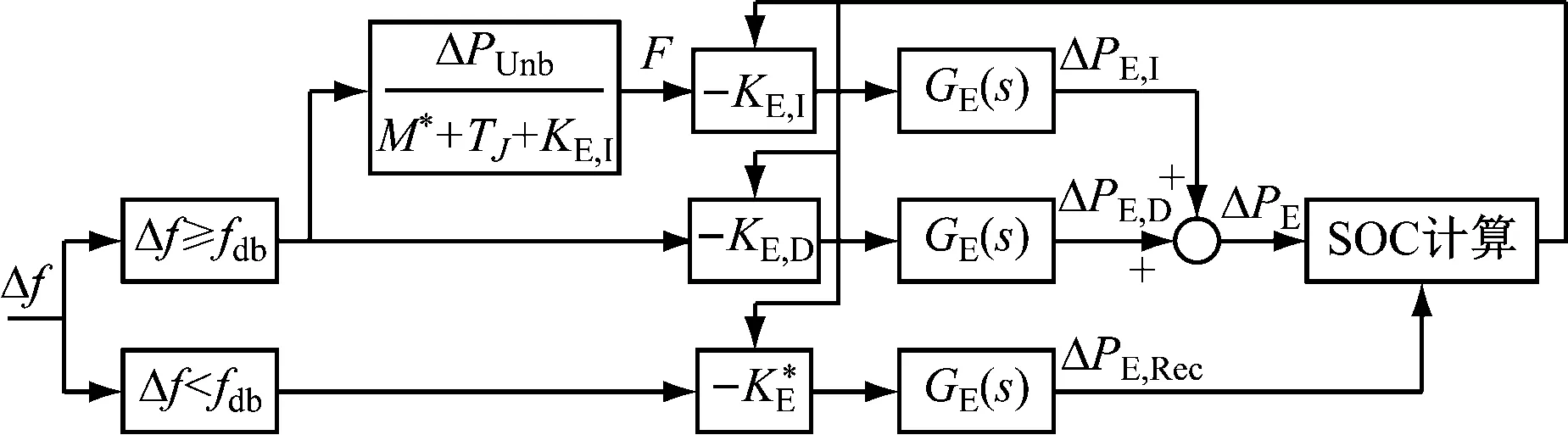
图2 储能系统自适应控制框图

2.2 源储协同一次调频控制策略

2.2.1 预测模型

当负荷发生随机波动时，交流电网具有一定的一次调频能力[25]，可简单等效为传统同步发电机组。则基于AMPC的电力系统调频控制框图如图3所示，其包括火电机组调频模型、BESS调频模型、风电场调频模型及AMPC。其中火电机组包括调速器模型Ggov(s)及再热锅炉和汽轮机模型Ggen(s)，KG为机组单位调节功率,TG为调速器时间常数，TE为储能出力时间常数，TRH为再热器时间常数，TCH为汽轮机时间常数，FHP为汽轮机再热器增益。

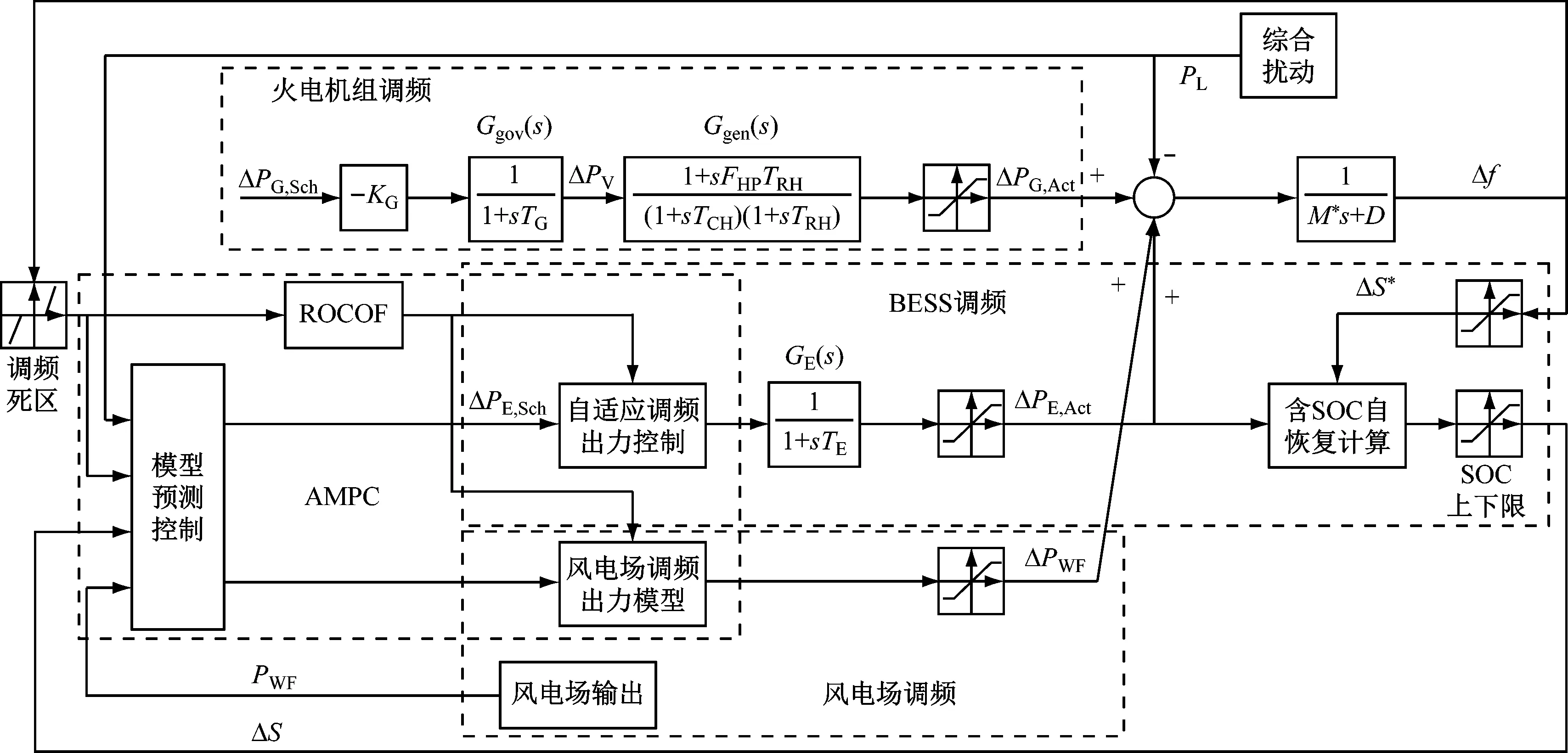
图3 AMPC电力系统调频控制框图

综合上述模型建立系统一次调频状态方程组：

(15)

式中：ΔPV为调速器出力变化量；ΔPG,Sch为火电机组计划出力变化量；ΔPG,Act为火电机组实际出力变化量；ΔPE,Sch为储能系统计划出力变化量；ΔPE,Act为储能系统实际出力变化量；ΔS为储能SOC的变化量。

基于模型预测控制的标准状态空间方程如下：

(16)

式中：xi为状态变量；ui为输入变量；ri为扰动变量；yi为输出变量；A、B、D、C均为相应变量的状态矩阵。

对式(15)进行离散化后每一步的预测状态为：

(17)

则其标准状态空间方程可转化为：

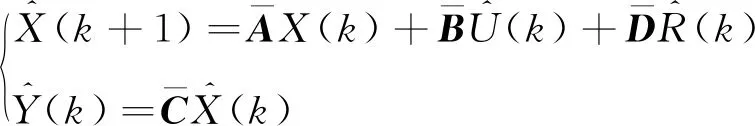
(18)

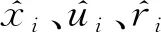
结合式(15)～式(18)和图2中的调频模型，可得系统状态变量X(k)、输入变量U(k)、输出变量Y(k)和扰动变量R(k)分别为：

(19)

2.2.2 目标函数及约束

上述源储协同调频模型的优化目标是分配各调频场站的出力，改善调频效果的同时提升风电的调频性能。因此，在目标函数中通过设置频率偏差ωf,k项来最小化系统频率在未来控制窗口内的频率偏移量，优化调频效果；设置储能计划功率偏差和火电机组计划功率偏差系数ωE,k项和ωG,k项来评估电池储能系统和火电机组实际输出功率相比计划功率所减少的能耗量，通过这2项可以在保证调频效果的同时提升风电的调频出力；设置SOC偏差ωSOC,k项来调节储能系统的SOC，使其保持在相对良好的水平以满足长时间连续调频的运行需求。

基于上述分析，预测控制的目标函数设定为：

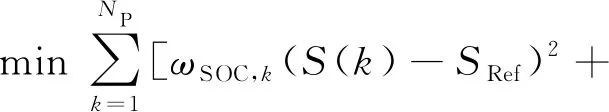
ωf,kΔf(k)2+ωE,k(PE,Act(k)-PE,Sch(k))2+

ωG,k(PG,Act(k)-PG,Sch(k))2]

(20)

s.t.

-10%PG,N≤ΔPG,Act(k+j|k)≤10%PG,N

-PE,N≤ΔPE,Act(k+j|k)≤PE,N

Smin≤ΔS(k+j|k)≤Smax

-10%PWF(k)≤ΔPWF(k+j|k)≤6%PWF(k)

式中：SRef为SOC参考值，设为0.5;PG,N、PE,N分别为火电机组和储能系统的额定功率；ΔPG,Act(k+j|k)、ΔPE,Act(k+j|k)、ΔS(k+j|k)和ΔPWF(k+j|k)分别为基于当前采样时刻k对k+j时刻火电机组实际出力、储能系统实际出力、储能SOC和风电场出力的预测值变化量。

4组权重系数均可以根据不同控制时刻设置不同的权重，考虑到系统运行的不确定性，为偏离当前时刻控制量较远的控制项设置较低权重系数，为较近的控制项设置较高权重系数[9]。

综上，AMPC调频控制策略构建完成，主要包括调频单元预测模型控制、风电场调频出力模型及储能系统自适应调频出力控制。风电场输出作为扰动变量的一部分，能够灵活参与调频，而整个控制策略可以根据当前风电场出力进行实时优化求解。

3 调频评价指标

电网中常见的扰动分为阶跃型负荷扰动和连续型负荷扰动。阶跃型负荷扰动通常对应于大容量电机的启停和故障甩负荷，发生速度较快且持续时间较短；连续型负荷扰动通常指没有跃变的连续性负荷变化，持续时间长但幅值趋于平缓[26]。根据标准GB/T 40595—2021[27]规定，分别提出对应的2类调频评价指标。

(1) 阶跃型负荷扰动评价指标

最大频率偏差Δfm、稳态频率偏差Δfs、一次调频响应滞后时间tp、一次调频上升时间tr、一次调频调节时间ts和超调量σ均如图4所示[27]，其中±Δ为一次调频稳态判定阈值，取±5%。

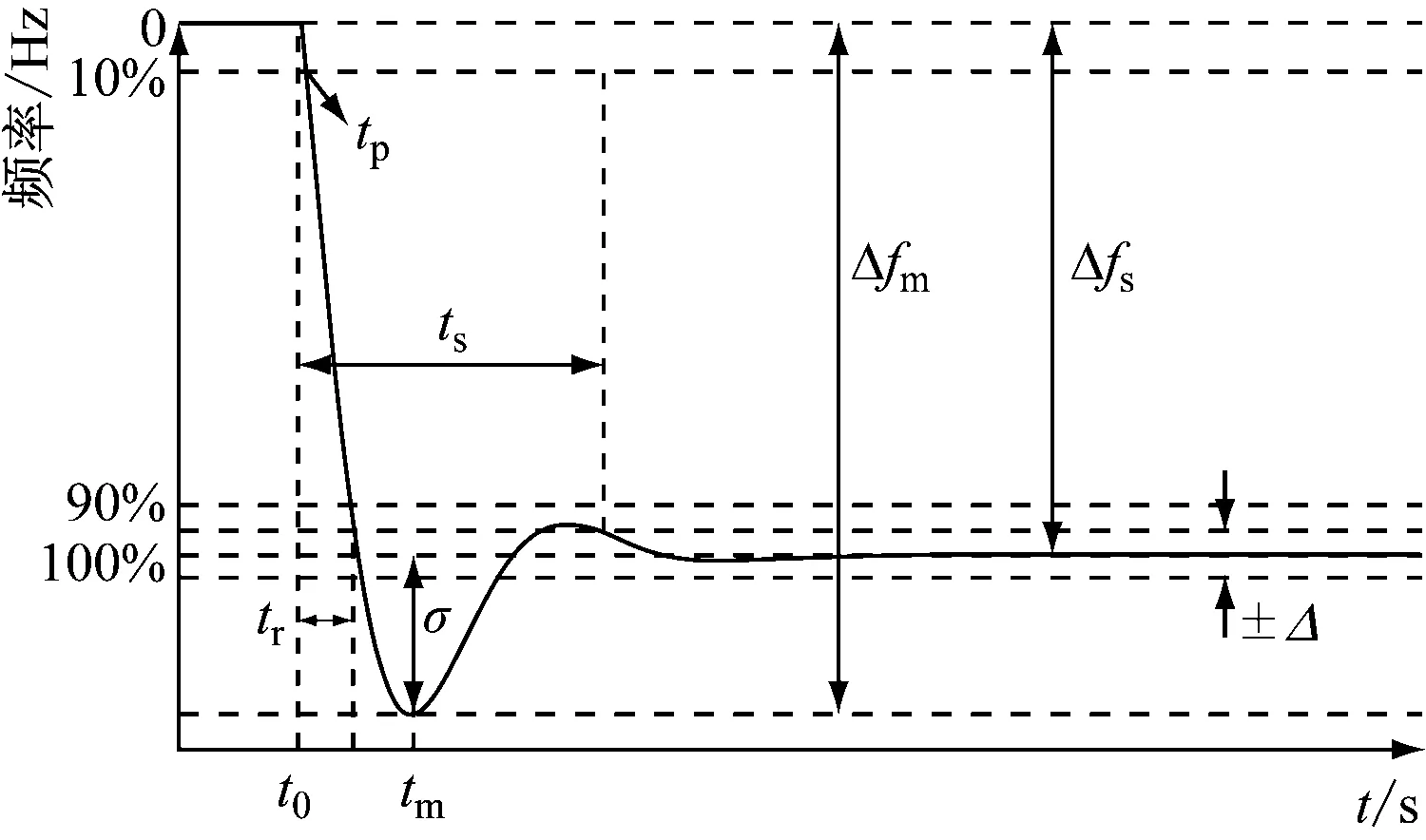
图4 阶跃型负荷扰动评价指标

频率平均跌落速度α和频率平均恢复速度β为：

(21)

式中：tm为达到最大频率偏差的时间；t0为阶跃扰动的起始时间。

频率平均跌落速度越小，给电网造成的调频压力就会越小，而频率平均恢复速度越快，则电网频率处于异常状态时间就越短。

(2) 连续型负荷扰动评价指标

选用频率偏差Δf的波动量和储能荷电状态SOC变化量的均方根作为连续型负荷扰动的评价指标。其中Qf反映了控制策略的综合调频效果，QS反映了控制策略的储能SOC保持效果。

(22)

式中：Δfi为采样点i的系统频率偏差；Si为采样点i的SOC值；N为采样点个数。

电量贡献指数Q%,X可以反映调频持续时间内，机组一次调频的实际贡献电量占比。

(23)

式中：QX为机组一次调频实际补偿电量，分别对应火电机组补偿电量QG、储能系统补偿电量QE以及风电场补偿电量QWF；QT为机组一次调频理论贡献电量；ΔPX,Act为机组调频实际出力，分别对应ΔPG,Act、ΔPE,Act和ΔPWF；ΔPT为机组调频理论出力对应的调整量；tb、te分别为调频开始和结束时刻；PN为机组额定功率；δ为转速不等率，取为5%。

4 仿真验证及结果分析

为验证所提源储协同一次调频策略的有效性，另外提出3组不同条件的组合作为对比，共同完成仿真试验：(1)火电机组独立一次调频；(2)加入储能系统并对其进行变K自适应控制[11]；(3)加入基于自适应控制的储能系统，同时增加风电场进行辅助调频；(4)对火电机组、储能系统及风电场同时进行自适应模型预测控制。

设置火电机组额定功率为1 000 MW，设为1，其余功率参数均是以该机组的额定功率为基准转化的标幺值；储能系统额定功率为10 MW(标幺值为0.01)，额定容量为1 MW·h(标幺值为0.001)；风电场额定功率为300 MW(标幺值为0.3)；电网额定频率为50 Hz，调频死区为±0.033 Hz；采样时间为0.1 s，详细参数见表1。根据风电场运行状况，风机输出超过额定功率80%的概率一般不超过10%[28]，且风机变桨控制响应速度较慢，因此在中低风速下主要考虑风机通过超速减载运行提供有功备用。

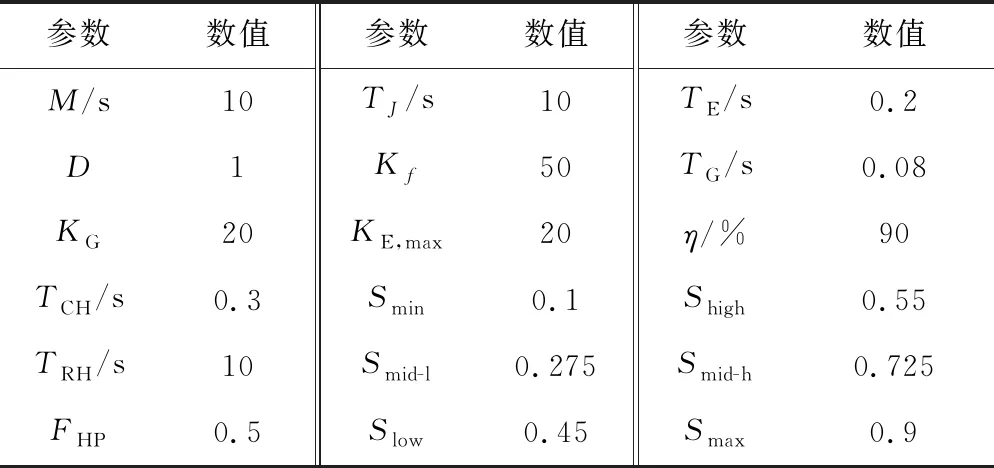
表1 仿真模型参数

4.1 阶跃扰动工况

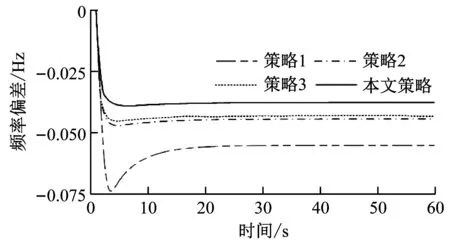
在t=1 s加入标幺值为0.01的阶跃扰动进行仿真试验，选取60 s的扰动工况。阶跃扰动一次调频指标见表2,各个机组的运行状态如图5所示，仿真时段风电场功率输出及ROCOF曲线如图6所示。

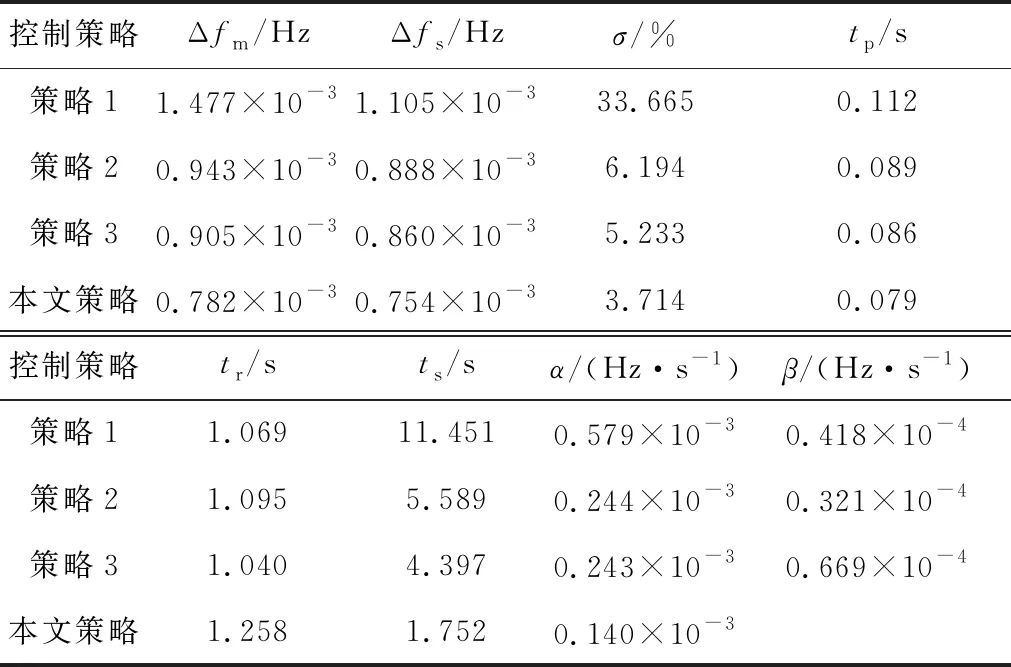
表2 阶跃扰动一次调频指标比较

从图5(a)可以看出，加入阶跃扰动的瞬间，4种策略下系统频率均快速下降。其中，本文策略频率下降幅度最小，结合表2可知，最大频率偏差仅为0.782×10-3Hz，相比其他3种策略分别减少47.05%、17.07%和13.59%，稳态频率偏差和超调量也都有相应幅度的减小。此外，储能系统的加入大幅提升了一次调频效果，缩短了一次调频时间； 风电场的加入则进一步优化了调频表现，但提升效果有限。对比策略3和本文策略，AMPC的加入再次大幅提升了系统的整体调频效果，调节时间减少60.15%，频率平均跌落速度下降42.39%，较大程度上减缓了系统的调频压力。对于频率平均恢复速度，本文策略工况下，由于超调量小于允许偏差±Δ，其一次调频调节时间ts小于最大偏差时间tm，即在达到最大频率偏差之前就已完成调频动作，所以不存在频率恢复速度β。

从图5(b)和图5(c)可以看出，AMPC控制的加入使得火电机组和储能系统均提前开始动作参与调频，且火电机组的功率提升速度明显放缓，相比其他策略一定程度上减轻了火电机组的增发压力。图6(b)给出了仿真时段风电场输出情况。该时段风电场输出远远偏离额定功率(标幺值为0.3)，调频资源不足；结合式(1)～式(5)以及图6(c)，AMPC使扰动加入瞬间系统的计划功率不平衡量得到削减，同时惯性系数变化导致ROCOF出现明显减幅，风电场惯性出力减少，最终通过控制储能和风电的输出功率来达到约束条件下的最优调频效果。

(a) 频率偏差

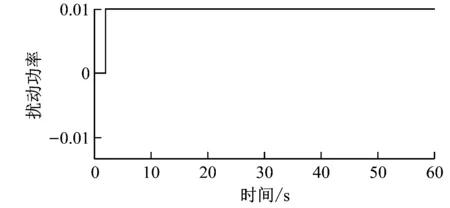
(a) 阶跃扰动功率

由于60 s的时间相对于储能的额定容量来说耗能太少，SOC变化不明显，将阶跃扰动的仿真时长延长至300 s来观察调频系数和SOC的变化情况，结果如图7所示。从图7可以看出本文策略中储能的变K自适应控制效果，随着SOC减小，调频系数也相应减小，呈现“S”形变化。1～<36 s内BESS电量充足，处于最大处理时段；36 s时SOC下降至Slow，随后功率调节系数按照式(9)减小，减少储能的调频出力，至168 s时SOC降至Smid-l；之后调频系数继续下降，SOC的衰减速度明显下降，大幅延长了储能放电时长，并防止储能系统过度放电。

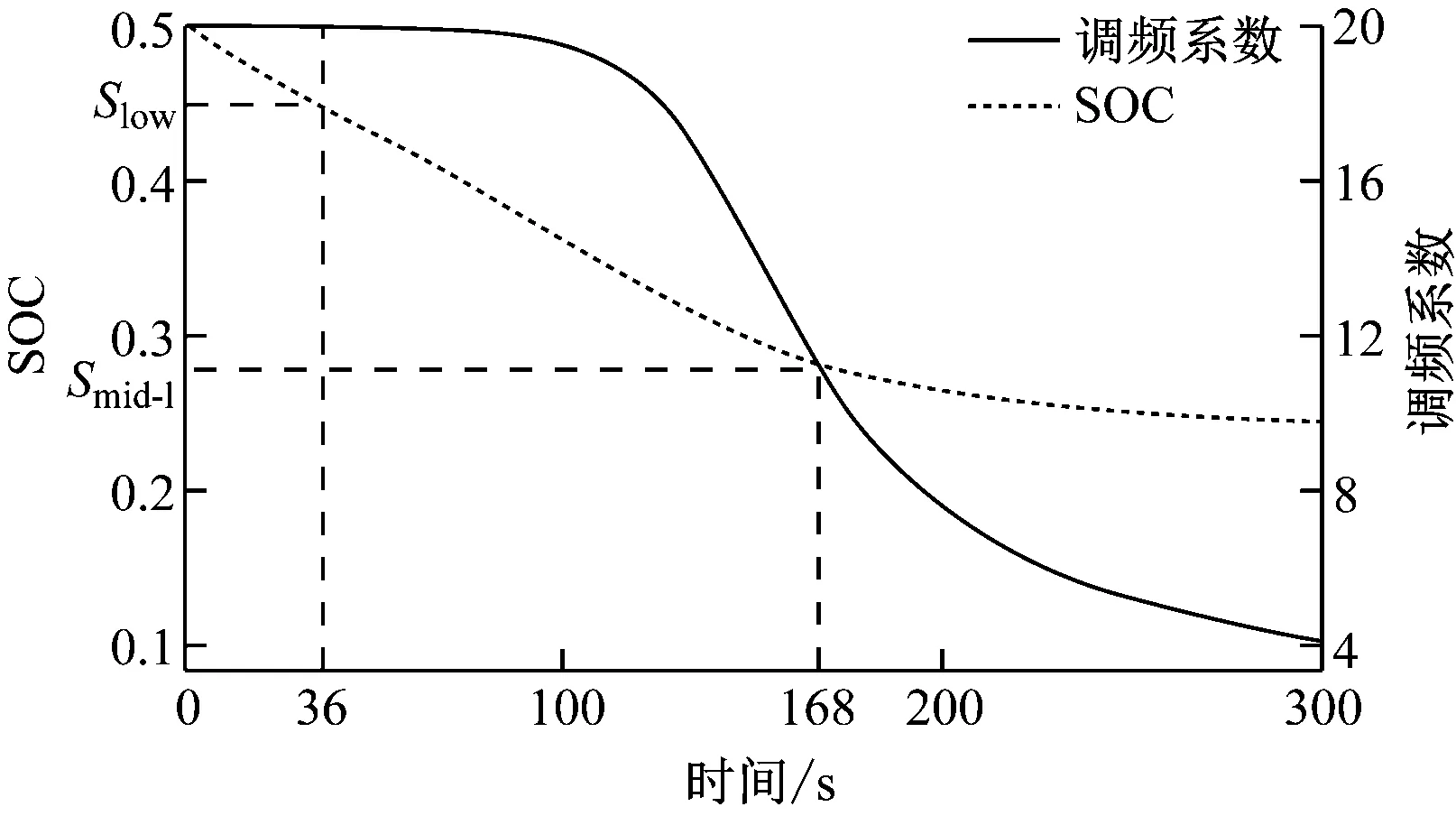
图7 阶跃型负荷扰动下储能SOC和调频系数

4.2 连续扰动工况

加入连续扰动进行仿真试验，选取300 s的扰动工况。火电机组和储能系统的出力情况及SOC变化曲线如图8所示。扰动负荷、风电场功率及ROCOF如图9所示。

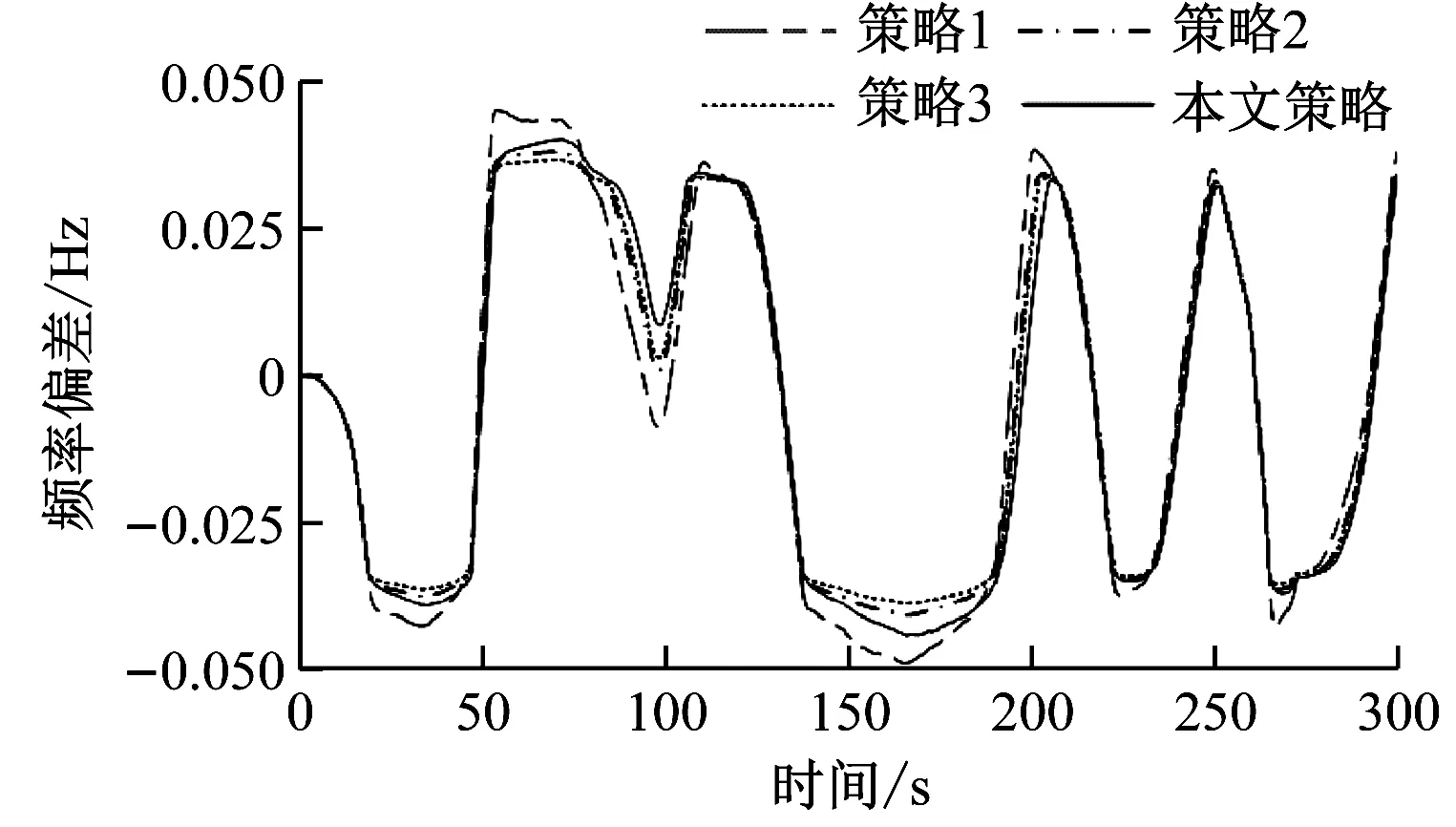
(a) 频率偏差

从图8(a)可以看出，连续扰动工况下策略2、策略3和本文策略的调频效果接近，均明显优于策略1。从图8(b)～图8(d)可以看出，类似于阶跃扰动工况，储能系统及风电场的加入大幅优化了系统调频效果，减少火电机组和储能的出力。而本文策略中AMPC的加入再次大幅降低火电机组的调频出力，机组动作次数减少、损耗降低；减少了储能出力，SOC状态更为健康，使用寿命延长，同时为后续调频提供备用资源；风电场的调频出力明显提升。

同时，从图9(b)可以看出，仿真时段风电场功率接近额定功率，风电调频资源充足；图9(c)中，AMPC的加入使得计划功率不平衡量在扰动量变化较快的时刻有所增加，对应时刻的ROCOF也相应增加，风电场惯性出力提升。

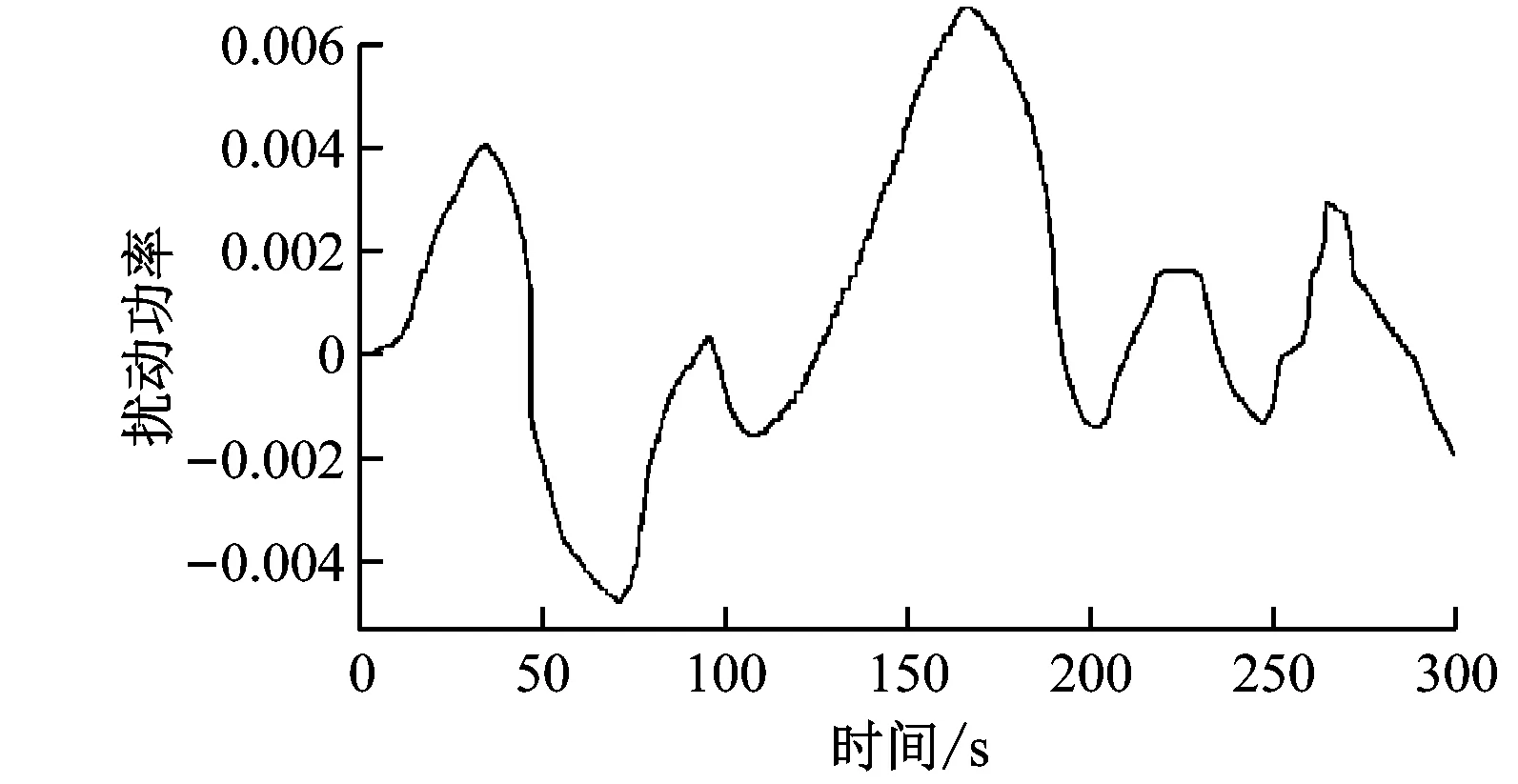
(a) 连续扰动功率

结合表3的调频指标可知，相比策略3，本文策略的综合调频效果再次得到优化，频率偏差波动量下降1.64%，SOC的状态提升18.13%；机组调频贡献电量方面，火电机组出力减少58.87%，储能出力减少29.39%，风电场出力增加69.67%。此外，储能通过自恢复控制的恢复电量情况见表4，结合图10可见，BESS在一次调频过程中随着时间尺度的增加恢复电量相对可观，一定程度上优化了SOC状态，提高了其后续调频能力。

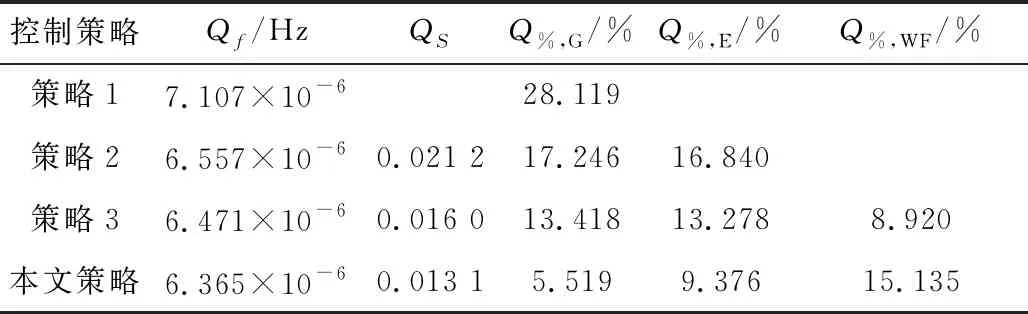
表3 连续扰动一次调频指标比较

表4 储能自恢复电量

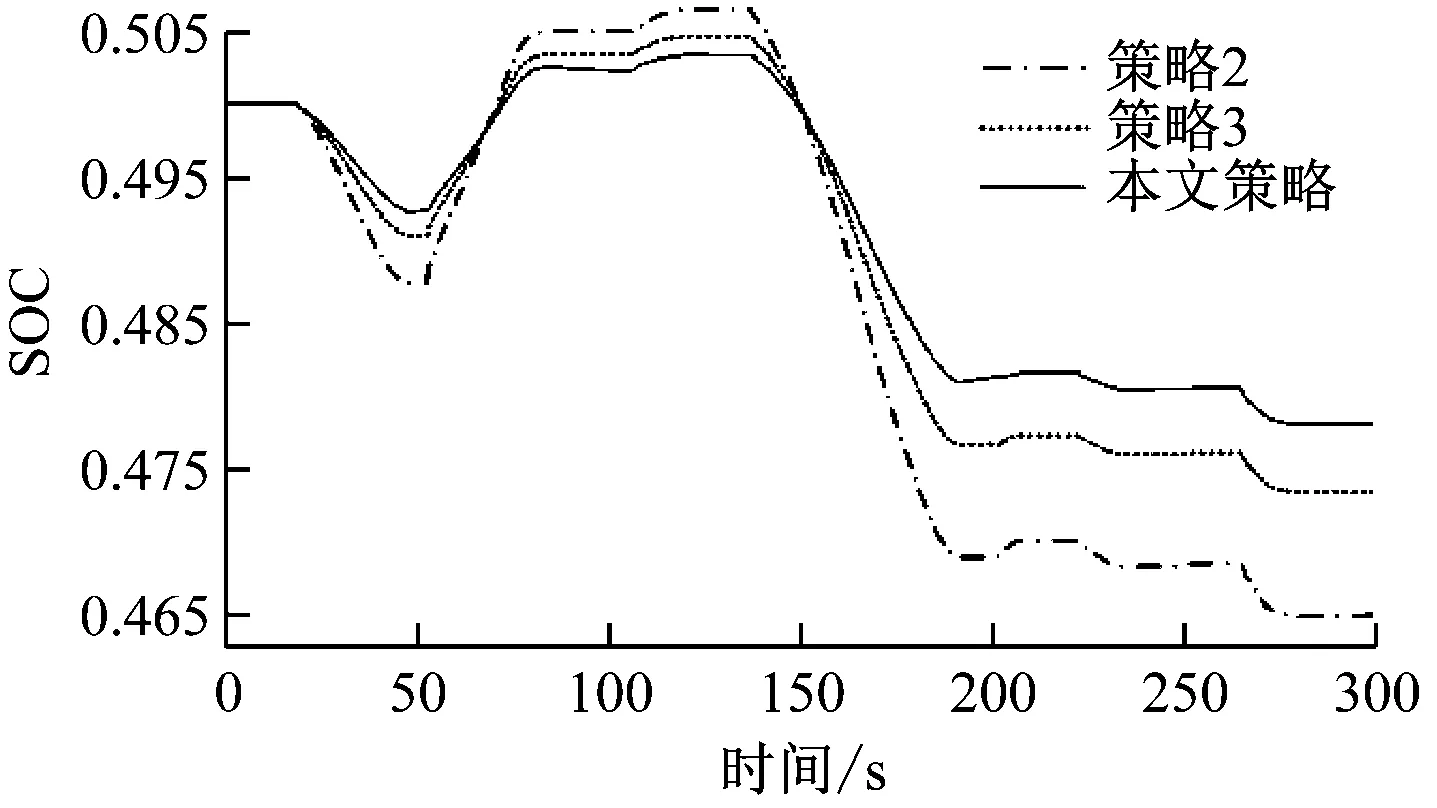
图10 连续型负荷扰动下储能SOC

5 结 论

(1) BESS及风电场出力的加入大幅缓解了传统火电机组的调频压力，阶跃和连续扰动下的一次调频效果明显提升。

(2) 提出的AMPC控制策略根据风电场输出及储能SOC状态实时预测并优化各场站的调频出力,提升调频效果。相比于仅加入自适应控制的源储协同调频，阶跃型负荷扰动下，调节时间减少60.15%，频率平均跌落速度下降42.39%；连续型负荷扰动下，频率偏差波动量下降1.64%。

(3) 本文策略使得风电场参与调频更加灵活，有效提升了风电的调频性能。相比于仅加入自适应控制的源储协同调频，为了达到约束条件下的最优调频效果，本文策略在阶跃型负荷扰动下，风电场输出大幅偏离额定功率导致调频资源不足，ROCOF减幅、风电场惯性出力减少；连续型负荷扰动下，风电场输出接近额定功率、调频资源充足，风电场调频出力增加69.67%。

电力系统调频涉及到多个能源单元，如何在众多并网能源中根据地理位置、调频成本、调频效果等匹配合适的能源进行协同调频来维持电网的安全稳定还有待进一步研究。