考虑频率响应分散性及系统分区的含风电系统等效惯量估计

李东东，董 楠，姚 寅，徐 波

考虑频率响应分散性及系统分区的含风电系统等效惯量估计

李东东，董 楠，姚 寅，徐 波

(上海电力大学电气工程学院，上海 200090)

随着电力系统中新能源机组渗透率的快速提高，系统惯量水平下降将威胁系统频率稳定性，惯量的空间分布特征也将更加凸显，频率响应的分散性将不能被忽略。针对以上问题，提出一种考虑频率响应分散性及系统分区的含风电电力系统等效惯量估计方法。首先，为降低频率响应分散性对估计精度的影响，基于谱聚类算法对电力系统进行分区，并基于皮尔逊相关系数定义频率相似度指标确定区域频率的最优测量节点。其次，由于测量所得的频率变化率(rate of change of frequency, RoCoF)曲线中包含大量的振荡分量，提出一种基于摇摆方程的数值积分方法估计区域及系统全局惯量。最后，在DIgSILENT/PowerFactory中建立改进IEEE10机39节点系统以验证所提方法的有效性。仿真结果表明，该方法适用于不同场景下含风电系统的等效惯量估计。

低惯量；惯量估计；区域惯量；频率分散性

0 引言

联合国大会上中国提出“双碳”目标，即2030年前碳排放达到峰值，2060年前实现碳中和，风电、光伏等新能源的装机容量将进一步增长[1]。新能源机组通常通过电力电子设备耦合到电网，难以提供惯量支撑[2]。近年来，系统惯量水平的下降被认为是将更多新能源接入系统的主要障碍之一[3-6]，2019年的英国“8·9”大停电事故就与故障发生时系统新能源高渗透导致的惯量支撑不足有关[7]。风电机组通过虚拟惯量控制等手段可提供虚拟惯量，虚拟惯量在形式以及响应特性上不同于传统电力系统的旋转惯量[8]。另外，风电机组集中接入区域的低惯量特征使得系统惯量的空间分布特性更加凸显[9]。因此，对含风电电力系统进行准确的惯量估计对风电接入比例的提高与系统安全稳定运行具有重要意义。

现有惯量估计方法大多针对系统层面的惯量估计[10-11]。文献[12]通过对扰动后总发电曲线及频率曲线进行多项式参数拟合从而估计系统惯量，但结果中只包括同步机提供的旋转惯量。互联系统的惯量通过与区域间振荡模式参数的关系来估计[13-14]，但其依据摇摆方程的状态变量是两区域等值机的角速度差，估计值意义不同于能量守恒得到的系统惯量。文献[15]利用赤池信息准则确定系统辨识模型阶次，利用所建立辨识模型的阶跃响应计算系统的等效惯量。

但是，上述方法未考虑区域间的惯量分布，通过等效公式能够用区域惯量计算系统等效惯量，而区域惯量不能由系统惯量推导出，因此区域惯量估计比系统惯量估计更加灵活[16-17]。文献[18]通过有功功率和频率扰动信息从辨识模型中提取区域惯量值，但系统中分区是给定的。文献[19]在无法得知扰动功率大小的情况下，利用差值计算法估计区域惯量。差值计算法利用RoCoF曲线两点间的差值，但RoCoF曲线中包含的振荡分量可能造成估计结果误差变大。文献[20]定义了节点惯量，节点惯量能够表示惯量的空间分布，但不能计算系统等效惯量。

由于电力系统中惯量分布不均匀，扰动后频率响应的离散性更加凸显[21]，选择不同的频率测量点时，惯量估计的误差具有随机性[22]。现有的系统惯量估计方法大多使用惯量中心频率[23-24]，惯量中心不是固定的频率测量点，惯量中心频率的计算需要已知各台发电机的母线频率和惯量。此外，风电机组等新能源机组提供的虚拟惯量一般是未知的，增加了惯量中心频率的计算难度。因此，需要选取合适的频率测量点以代替惯量中心。文献[25]提出惯量图心的定义以降低频率分布特性对惯量估计结果精度的影响，但该方法仍需已知单台发电机的惯量，且没有考虑区域惯量。文献[19]中惯量估计采用主导机组母线处所测频率，但用单台发电机母线频率代替所有发电机母线频率的加权平均值，其准确性仍有待验证。

针对现有研究存在的不足，本文开展了以下研究。首先，借助谱聚类算法实现分区，定义区域节点频率相似度指标，确定各区域的频率测量节点。该方法能够降低频率响应的分散性对估计精度的影响。然后，使用基于数值积分方法的区域惯量估计公式，对滑动窗口的估计结果进行数据处理，以估计出区域惯量和系统全局惯量。最后，采用改进的IEEE10机39节点系统模型，仿真验证了所提惯量估计方法在多种场景下的有效性。

1 系统惯量理论

1.1 惯量估计原理

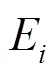
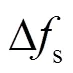
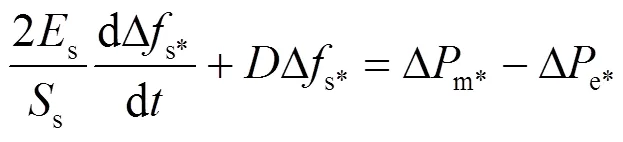
1.2 风电接入下电力系统的等效惯量

大规模新能源机组并网使现代电力系统呈现低惯量特征，考虑系统稳定运行的频率要求，亟需对经电力电子器件接入电网的风电机组、光伏等进行虚拟惯量控制。图1为电力系统惯量的来源。电源侧转动惯量主要来源于火电机组，虚拟惯量主要来源于风电机组，这是由于风电机组本身存储了大量动能，负荷侧惯量主要来源于感应电动机的转动惯量。

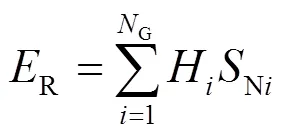
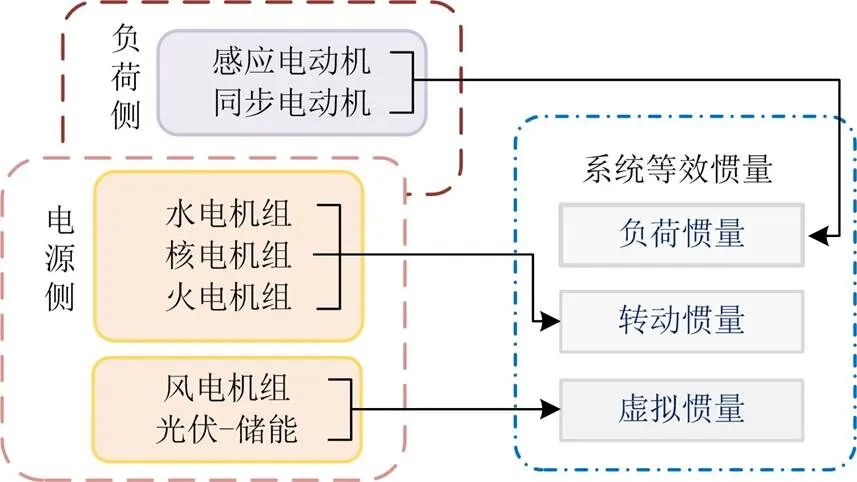
图1 电力系统惯量的来源

2 惯量估计

系统惯量是电网频率稳定性的一个整体指标，虽然能够用来评估整个系统的稳定运行能力，但难以衡量不同区域稳定性。本节提出一种基于系统分区的惯量估计方法，以降低频率响应分散性的影响，估计结果及分析还可为系统频率稳定性的提高、风机的接入位置提供更多的参考信息。

2.1 系统分区与区域频率测量点选取

2.1.1基于谱聚类算法的电力系统分区

电力系统一般根据地理位置或运行人员的经验进行区域划分，但随着电网结构复杂度的增加，对区域划分的结果与内部结构的一致性提出更高的要求。电力系统网络可以自然地表示为一张图，谱聚类算法是由图论发展而来的一种算法，并在大多数情况下，聚类效果优于传统的聚类算法[29]。通过谱聚类算法实现电力系统分区后，各区域内的节点高度连接，能够反映电网的内部结构。

图2 系统分区的流程图

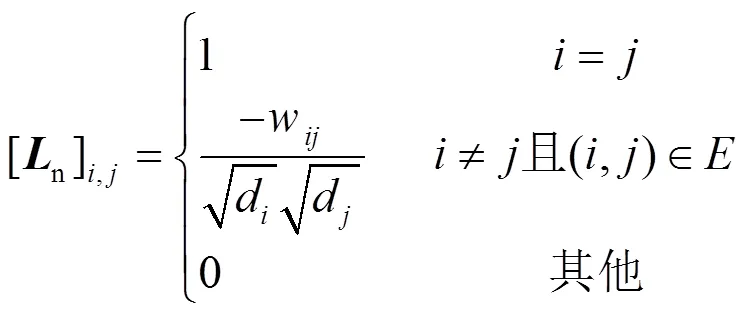
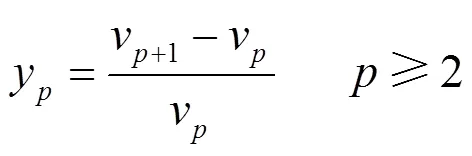
最后，使用k-means聚类达到加强聚类的目的[32]。k-means聚类算法的最优分区数根据CH指标选择，输出结果为每个节点对应的分区。

文献[33]中的CH(Calinski-Harabaz)指标同时考虑了簇内平方误差(within-group sum of squares, WGSS)和类间平方误差(between-group sum of squares, BGSS)，可用来评价聚类的效果。CH指标越大，聚类结果越优，取CH曲线的极大值对应的分区结果。

2.1.2基于皮尔逊相关系数的区域频率测量点选取

由扰动引起的机电瞬态过程以机电波的形式传播[34]，只有在网络中相对紧密耦合的区域，频率响应的相似度才会高[30]。与整个系统相比，虽然各区域中频率响应的分散程度降低，但是任意选择区域频率的测量点会产生随机误差，有必要在每个区域中选择合理的频率测量点。

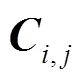
2.2 基于数值积分方法估计区域及系统等效惯量

在第2.1节基础上，电力系统可以看作通过网络耦合的多台等值发电机。电力系统中各区域惯量大小体现在有功-频率的动态响应中，如图3所示。通过测量得到的各区域有功功率和频率数据估计区域惯量，等值发电机的摇摆方程为

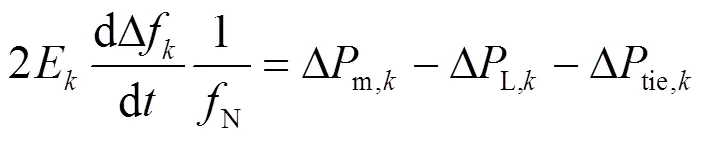
式中：为区域k的等效惯量；为区域频率偏差；为系统额定频率；为区域k内同步发电机总的机械功率增量；为区域k内的负荷增量；为区域k的联络线功率增量。

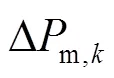
由于各区域之间存在动态相互作用，在一次调频响应动作前联络线功率随时间而不断变化，与各区域的惯量响应有关。联络线功率变化难以用以时间为变量的函数表达式表示，可采用复化梯形求积公式进行数值积分运算，如式(10)所示。

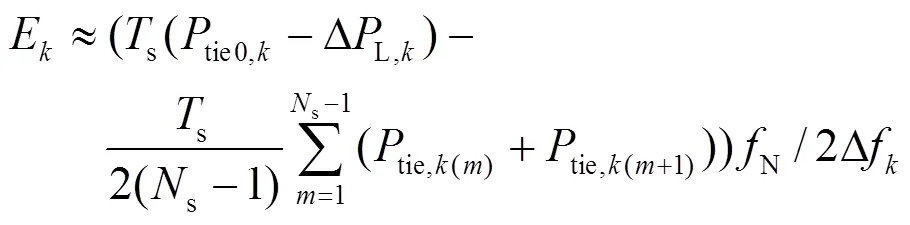
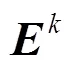
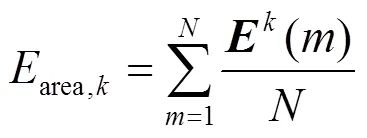
区域与系统等效惯量估计的流程总结如下：

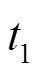
3) 将惯量估计时间窗口向后滑动，每隔0.1 s执行一次惯量估计，直到超出测量数据的时间范围，从而得到向量。

5) 重复步骤2)、3)、4)，直到估计出所有区域的等效惯量，用等效公式式(12)计算电力系统等效惯量。

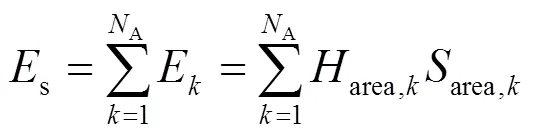
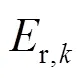
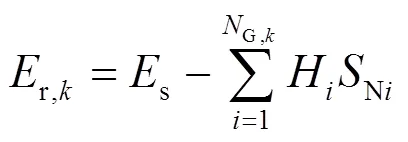
3 仿真验证

3.1 仿真系统

在DIgSILENTTMPowerFactory®中建立改进的IEEE10机39节点系统，图4是该系统的网络拓扑图。IEEE10机39节点系统是实际电力系统的简化模型，该系统的电压水平为345 kV，发电机G01为外部电网的等值机。为模拟风电接入，对IEEE10机39节点系统进行了如下修改：发电机G03、G07、G08分别被130台、112台、108台单台容量为5.556 MVA、输出功率为5 MW的双馈风力发电机组代替。为验证区域惯量估计方法的有效性，对大扰动下频率动态响应过程进行仿真，考虑了频率测量点、惯量估计时间窗口长度、惯量源等多重因素对惯量估计结果的影响。

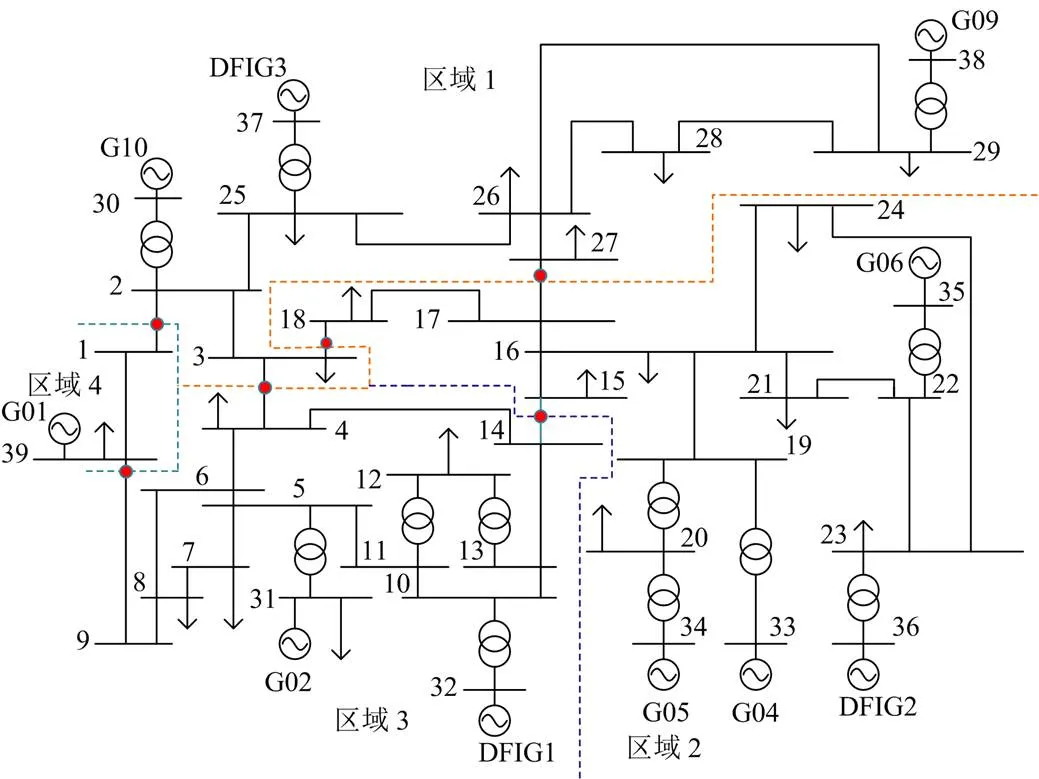
图4 改进的IEEE10机39节点系统

3.2 系统分区与区域频率测量点选取

根据图2所示的流程图，将电力系统网络图的边权设为电力传输线路阻抗值的倒数，构建邻接矩阵，以表示系统任意两节点间的内在联系紧密程度。利用谱聚类算法对电力系统中所有节点进行聚类，该系统划分为4个区域时，CH指标取为CH曲线的极大值，分区结果如表1所示。由于发电机G01是外部等值机组，所以发电机节点39与节点1组成区域4。区域1包括发电机G09、发电机G10和风电机组DFIG3，风电容量占比为23%。区域2包括发电机G04、发电机G05、发电机G06、发电机G07和风电机组DFIG2，风电容量占比为22%。区域3包括发电机G02和风电机组DFIG1，风电容量占比为51%。由表1可知，4个区域之间共有6条联络线，需要配置测点用于联络线功率测量。

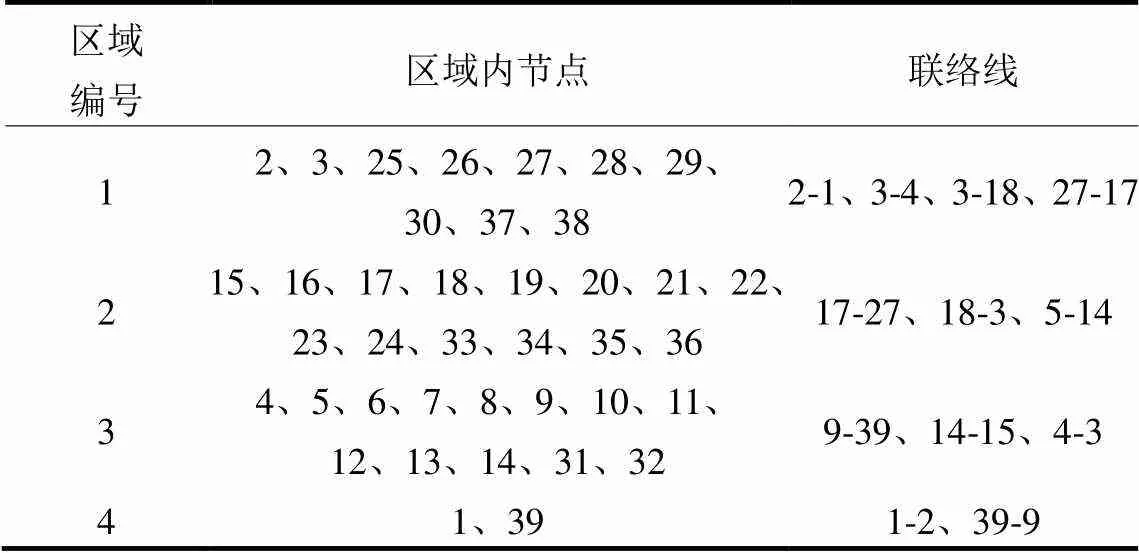
表1 谱聚类分区结果

表2 各区域选取的Dmax节点及其选择概率

3.3 惯量估计结果分析

3.3.1验证区域频率测量点选取合理性

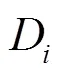
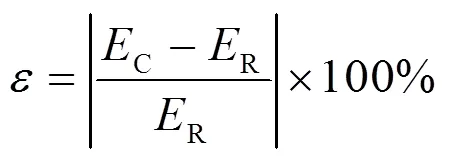
式中，为惯量估计值。

3.3.2惯量估计方法的有效性验证

为了验证所提惯量估计方法的有效性，设置了以下3种不同的负荷阶跃扰动：①Bus18处突增负荷500 MW；②Bus04处突减负荷300 MW；③Bus27处突增负荷300 MW。系统负荷均为恒功率负荷，扰动发生后的系统频率曲线如图6所示，系统频率为计算得到的惯量中心频率，通过计算各发电机频率的加权平均值得到。扰动2与扰动3的扰动功率相同，频率曲线呈对称形态，扰动1的系统频率曲线相对于扰动2整体下移。惯量估计的结果和误差汇总见表3。

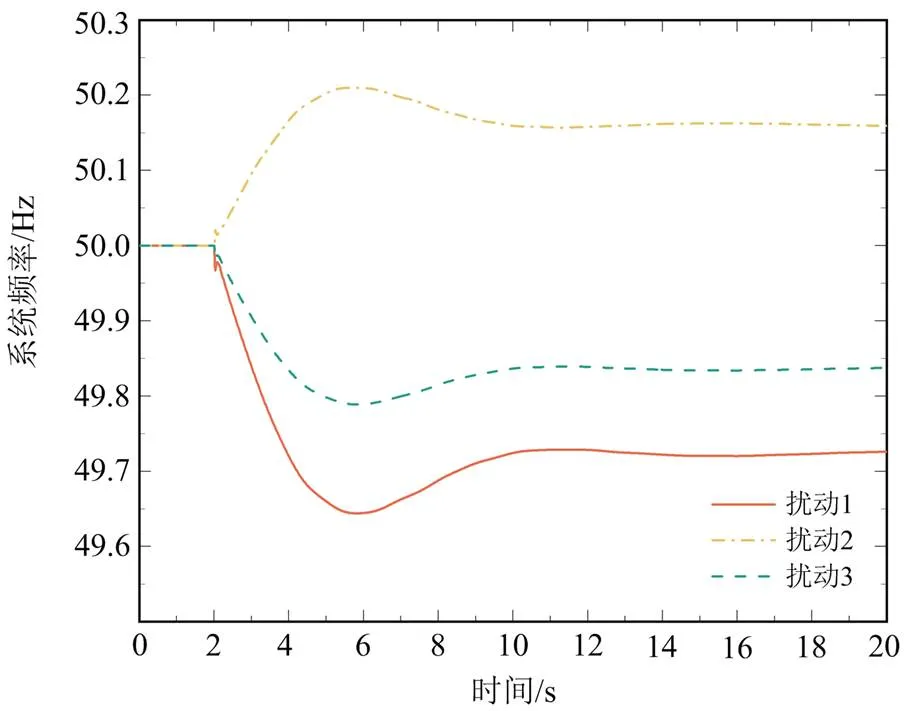
图6 扰动发生后的系统频率曲线

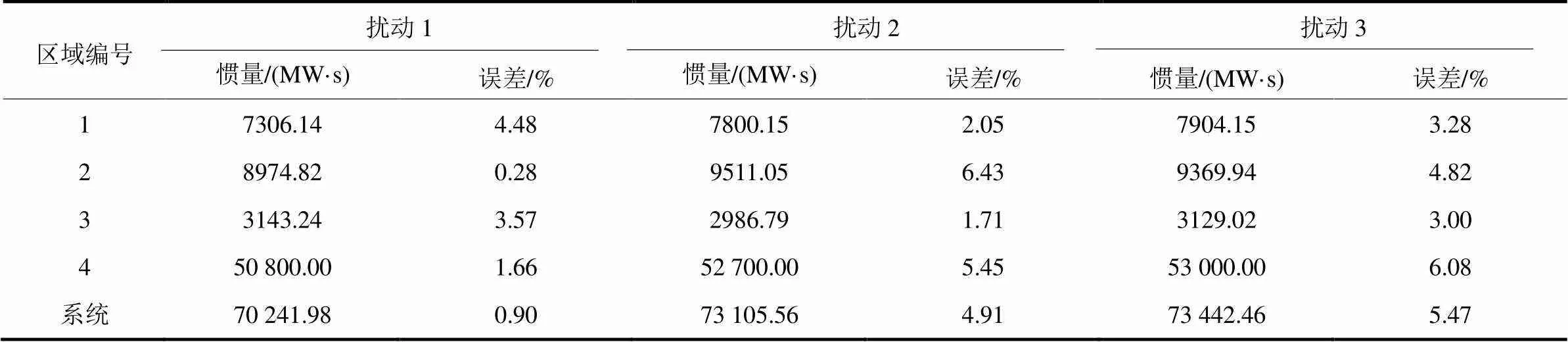
表3 惯量估计结果及误差

由表3可知，区域惯量的最大估计误差为6.43%，最小仅为0.28%，电力系统估计值的误差低于6%，本文提出的惯量估计方法在不同位置、不同大小的扰动下准确度均较高。由于区域4的惯量大于其他3个区域，估计结果受区域4惯量估计值影响最大。

3.3.3考虑多种惯量源的惯量估计

设置扰动为Bus27突增负荷300 MW，考虑以下3种场景，对含不同惯量源的系统进行惯量估计，结果如表4所示。场景2、场景3在场景1系统的基础上分别考虑了需求侧与风电机组的惯量贡献。

表4 不同场景下的惯量估计结果

1) 场景1：改进的IEEE10机39节点系统，系统负荷均采用恒功率负荷模型。

2) 场景2：改进的IEEE10机39节点系统，系统负荷均采用感应电动机负荷模型。感应电动机模型采用DIgSILENT通用负荷模型的动态部分[36]，负荷随频率的变化而动态变化。

3) 场景3：改进的IEEE10机39节点系统，系统负荷均采用恒功率负荷模型，对风电机组施加虚拟惯量控制，输出功率可响应频率变化率。

场景1的估计结果仅包含同步发电机提供的转动惯量，区域惯量估计值的误差为3.00%~6.08%，系统惯量的估计误差为5.47%。场景2中除同步机提供的转动惯量外，需求侧的感应电动机也可提供等效惯量支撑。场景2的惯量估计值减去场景1中对应的同步惯量值，即可得到负荷的惯量贡献。场景2中，约4%的系统惯量由需求侧提供，尤其是区域3的总惯量中约有13%为负荷惯量。因此，对于风电渗透率较高的系统，需求侧的惯量贡献不容忽略。

场景3的惯量源包括提供虚拟惯量的双馈风机，根据式(13)，虚拟惯量通过场景3的惯量估计值减去场景1中对应的同步惯量得到。场景3中，约6%的系统惯量来源于风电机组，各区域的虚拟惯量分别约为总区域惯量的19%、20%、39%、0%。此外，惯量空间分布的分散程度下降，区域等效惯量的标准差从20 138.24 MW·s下降到19 381.13 MW·s。

3.3.4不同惯量估计时间窗口长度下的惯量估计结果

将扰动设置为Bus18处突增负荷500 MW，为分析选择不同长度的惯量估计时间窗口对估计结果的影响，0.2 s、0.3 s、0.4 s、0.5 s 4种长度的时间窗口下各区域惯量及系统全局惯量的估计误差如图7所示。

图7 不同惯量估计时间窗口长度下的惯量估计结果

由图7可以看出，与真实值相比较，采用不同长度的惯量估计时间窗口时的估计结果略有区别。当惯量估计时间窗口长度为0.5 s时，系统惯量的估计误差最大为2.18%，区域惯量的最大估计误差为8.84%。当惯量估计时间窗口长度为0.4 s时，系统惯量的估计误差最低。总体而言，惯量估计结果的误差小于10%，且系统全局惯量的估计误差低于区域惯量估计误差的最大值。由此可见，该方法可以降低扰动后0~2 s内激活的一次调频响应对惯量估计结果的影响。

3.3.5分区方法的有效性验证

在本小节中利用第2.2节提出的方法进行惯量估计，对本文谱聚类分区算法与文献[17]中的分区方法以及系统不分区情况下的系统等效惯量估计结果进行对比分析。设置扰动为Bus27处突增负荷300 MW，负荷均为恒功率负荷，不同分区方法下的惯量估计结果如表5所示。

表5 不同分区方法下的惯量估计结果

由表5可知：系统不分区时的系统等效惯量估计误差为9.09%；文献[17]所提的分区方法下误差为4.31%；采用本文谱聚类分区算法时的估计误差为3.53%，精确度较高。与系统不分区时相比，本文采用的分区方法将整个系统等效为通过网络耦合的多个等值发电机，能够提高系统等效惯量的估计精度。与文献[17]分区方法相比，分区结果与本文中结果基本一致，系统等效惯量的估计误差相差较小，本文分区方法有一定的改进。综上，本文谱聚类分区算法作为分区惯量估计的前置步骤比较合适。今后将从改进分区方法的思路出发，进一步研究提高惯量估计结果准确性的方法。

本文提出的分区惯量估计方法准确度较高，估计结果包含多种惯量源。经仿真证明，该估计方法具有较强的适应性，与传统方法相比，该方法使用最优区域频率测量节点，需要更少的频率数据。

4 结论

本文基于系统分区提出了一种适用于含风电电力系统的等效惯量估计方法，主要考虑了频率响应分散性的影响，主要研究结论如下：

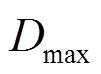
2) 提出的区域惯量估计公式用频率偏差代替RoCoF，以减少数据噪声的影响。在不同的惯量估计时间窗口长度或阶跃负荷功率扰动下，惯量估计结果的准确度均较高，仿真验证了方法的有效性。

3) 惯量估计值包括除同步发电机外其他惯量源的惯量贡献。在风电机组提供惯量支撑的情况下，惯量空间分布的分散程度下降。

本文研究可为准确估计系统等效惯量及区域惯量提供理论支撑。未来研究方向为通过人工智能算法和数据驱动算法实现惯量在线识别与预测。

[1] 谭显东, 刘俊, 徐志成, 等.“双碳”目标下“十四五”电力供需形势[J]. 中国电力, 2021, 54(5): 1-6.

TAN Xiandong, LIU Jun, XU Zhicheng, et al. Power supply and demand balance during the 14th five-year plan period under the goal of carbon emission peak and carbon neutrality[J]. Electric Power, 2021, 54(5): 1-6.

[2] 江涵, 岳程燕, 严兴煜, 等. 高比例可再生能源系统惯量约束对灵活性分析的影响研究[J]. 电力系统保护与控制, 2021, 49(18): 44-51.

JIANG Han, YUE Chengyan, YAN Xingyu, et al. Influence of system inertia on flexibility resource analysis for an interconnection system with a high proportion of intermittent renewable energy[J]. Power System Protection and Control, 2021, 49(18): 44-51.

[3] DU Pengwei, MATEVOSYAN J. Forecast system inertia condition and its impact to integrate more renewables[J]. IEEE Transactions on Smart Grid, 2017, 9(2): 1531-1533.

[4] 李东东, 刘强, 徐波, 等. 考虑频率稳定约束的新能源电力系统临界惯量计算方法[J]. 电力系统保护与控制, 2021, 49(22): 24-33.

LI Dongdong, LIU Qiang, XU Bo, et al. New energy power system critical inertia estimation method considering frequency stability constraints[J]. Power System Protection and Control, 2021, 49(22): 24-33.

[5] 周涛, 刘子诚, 陈中, 等. 异步电机频率支撑能力分析及其等效惯量评估[J]. 电力工程技术, 2022, 41(4): 18-24, 107.

ZHOU Tao, LIU Zicheng, CHEN Zhong, et al. Frequency support capacity of asynchronous motor andits equivalent inertia evaluation[J]. Electric Power Engineering Technology, 2022, 41(4): 18-24, 107.

[6] 胥心怡, 武家辉, 姚磊, 等. 基于协同惯量控制的双馈风机并网系统稳定性分析[J]. 电力建设, 2021, 42(12): 59-67.

XU Xinyi, WU Jiahui, YAO Lei, et al. Stability analysis of DFIG grid-connection system applying cooperative inertia control[J]. Electric Power Construction, 2021, 42(12): 59-67.

[7] 王博, 杨德友, 蔡国伟. 高比例新能源接入下电力系统惯量相关问题研究综述[J]. 电网技术, 2020, 44(8): 2998-3007.

WANG Bo, YANG Deyou, CAI Guowei. Review of Research on power system inertia related issues in the context of high penetration of renewable power generation[J]. Power System Technology, 2020, 44(8): 2998-3007.

[8] GABER M, ABUALKASIM B, MOHAMMED A. Superconducting energy storage technology-based synthetic inertia system control to enhance frequency dynamic performance in microgrids with high renewable penetration[J]. Protection and Control of Modern Power Systems, 2021, 6(4): 460-472.

[9] WU Di, JAVADI M, JIANG J N. A preliminary study of impact of reduced system inertia in a low-carbon power system[J]. Journal of Modern Power Systems and Clean Energy, 2015, 3(1): 82-92.

[10] CHASSIN D P, HUANG Z, DONNELLY M K, et al. Estimation of WECC system inertia using observed frequency transients[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1190-1192.

[11] WALL P, TERZIJA V. Simultaneous estimation of the time of disturbance and inertia in power systems[J]. IEEE Transactions on Power Delivery, 2014, 29(4): 2018-2031.

[12] PHURAILATPAM C, RATHER Z H, BAHRANI B, et al. Measurement-based estimation of inertia in AC microgrids[J]. IEEE Transactions on Sustainable Energy, 2019, 11(3): 1975-1984.

[13] CAI G, WANG B, YANG D, et al. Inertia estimation based on observed electromechanical oscillation response for power systems[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4291-4299.

[14] YANG D, WANG B, MA J, et al. Ambient-data-driven modal-identification-based approach to estimate the inertia of an interconnected power system[J]. IEEE Access, 2020, 8: 118799-118807.

[15] 徐波, 章林炜, 俞向栋, 等. 基于系统辨识的电力系统惯量在线评估改进方法[J]. 电力系统保护与控制, 2021, 49(18): 62-69.

XU Bo, ZHANG Linwei, YU Xiangdong, et al. An improved method of power system inertia online estimation based on system identification[J]. Power System Protection and Control, 2021, 49(18): 62-69.

[16] ASHTON P M, SAUNDERS C S, TAYLOR G A, et al. Inertia estimation of the GB power system using synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2014, 30(2): 701-709.

[17] WILSON D, YU J, AL-ASHWAL N, et al. Measuring effective area inertia to determine fast-acting frequency response requirements[J]. International Journal of Electrical Power & Energy Systems, 2019, 113: 1-8.

[18] 李世春, 夏智雄, 程绪长, 等. 基于类噪声扰动的电网惯量常态化连续估计方法[J]. 中国电机工程学报, 2020, 40(14): 4430-4439, 4723.

LI Shichun, XIA Zhixiong, CHENG Xuchang, et al. Continuous estimation method of power grid inertia normalization based on noise-like disturbance[J]. Proceedings of the CSEE, 2020, 40(14): 4430-4439, 4723.

[19] 刘方蕾, 胥国毅, 王凡, 等. 基于差值计算法的系统分区惯量估计方法[J]. 电力系统自动化, 2020, 44(20): 46-53.

LIU Fanglei, XU Guoyi, WANG Fan, et al. Assessment method of system partition inertia based on differential calculation method[J]. Automation of Electric Power Systems, 2020, 44(20): 46-53.

[20] ZENG Fanghong, ZHANG Junbo, ZHOU Yang, et al. Online identification of inertia distribution in normal operating power system[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3301-3304.

[21] 吴雪莲, 李兆伟, 刘福锁, 等. 大功率扰动下计及系统频率分布特性的紧急控制策略研究[J]. 电力系统保护与控制, 2021, 49(3): 104-114.

WU Xuelian, LI Zhaowei, LIU Fusuo, et al. Analysis of the emergency control strategy of system frequency considering system frequency distribution characteristics under large power disturbance[J]. Power System Protection and Control, 2021, 49(3): 104-114.

[22] ØRUM E, KUIVANIEMI M, LAASONEN M, et al. Future system inertia[J]. ENTSOE, 2015: 1-58.

[23] TUTTELBERG K, KILTER J, WILSON D, et al. Estimation of power system inertia from ambient wide area measurements[J]. IEEE Transactions on Power Systems, 2018, 33(6): 7249-7257.

[24] ZHANG J, XU H. Online identification of power system equivalent inertia constant[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8098-8107.

[25] 李东东, 张佳乐, 徐波, 等. 考虑频率分布特性的新能源电力系统等效惯性评估[J]. 电网技术, 2020, 44(8): 2913-2921.

LI Dongdong, ZHANG Jiale, XU Bo, et al. Equivalent inertia assessment in renewable power system considering properties of distributed frequency[J]. Power System Technology, 2020, 44(8): 2913-2921.

[26] CHASSIN D P, HUANG Z, DONNELLY M K, et al. Estimation of WECC system inertia using observed frequency transients[J]. IEEE Transactions on Power Systems, 2005, 20(2): 1190-1192.

[27] ZOGRAFOS D, GHANDHARI M, ERIKSSON R. Power system inertia estimation: utilization of frequency and voltage response after a disturbance[J]. Electric Power Systems Research, 2018, 161: 52-60.

[28] 王玎, 袁小明. 异步电机机电时间尺度有效惯量评估及其对可再生能源并网系统频率动态的影响[J]. 中国电机工程学报, 2018, 38(24): 7258-7266, 7452.

WANG Ding, YUAN Xiaoming. Available inertia estimation of induction machine in electromechanical timescale and its effects on frequency dynamics of power systems with renewable energy[J]. Proceedings of the CSEE, 2018,38(24): 7258-7266, 7452.

[29] DING L, GONZALEZ-LONGATT F M, WALL P, et al. Two-step spectral clustering controlled islanding algorithm[J]. IEEE Transactions on Power Systems, 2012, 28(1): 75-84.

[30] LARA-JIMENEZ J D, RAMREZ J M, MANCILLA- DAVID F. Allocation of PMUs for power system-wide inertial frequency response estimation[J]. IET Generation, Transmission & Distribution, 2017, 11(11): 2902-2911.

[31] MILANO F, ORTEGA Á. Frequency divider[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1493-1501.

[32] SÁNCHEZ-GARCÍA R J, FENNELLY M, NORRIS S, et al. Hierarchical spectral clustering of power grids[J]. IEEE Transactions on Power Systems, 2014, 29(5): 2229-2237.

[33] CALIŃSKI T, HARABASZ J. A dendrite method for cluster analysis[J]. Communications in Statistics-theory and Methods, 1974, 3(1): 1-27.

[34] YOU Shutang, LIU Yong, KOU Gefei, et al. Non- identification of inertia distribution change in high renewable systems using distribution level PMU[J]. IEEE Transactions on Power Systems, 2017, 33(1): 1110-1112.

[35] ASHTON P M, TAYLOR G A, IRVING M R, et al. Novel application of detrended fluctuation analysis for state estimation using synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1930-1938.

[36] 王莉丽, 刘崇茹. DIgSILENT在电力系统稳定计算中的应用[J]. 中国科技论文, 2016, 11(11): 1283-1287.

WANG Lili, LIU Chongru. Application of digsilent in power system stability calculation[J]. China Science Paper, 2016, 11(11): 1283-1287.

Equivalent inertia estimation of a power system containing wind power considering dispersion of frequency response and system partitioning

LI Dongdong, DONG Nan, YAO Yin, XU Bo

(College of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China)

With the rapid increase of the penetration rate of renewable energy sources in the power system, the decrease of system inertia will threaten frequency stability. Moreover, the spatial distribution characteristic of inertia will be more evident and the dispersion of frequency response cannot be ignored. An equivalent inertia estimation method for the system containing wind power considering the influence of the dispersion of frequency response and system partitioning is proposed. First, in order to reduce the influence of the dispersion of frequency response on estimation accuracy, the power system is partitioned based on a spectral clustering algorithm. A frequency similarity index is defined based on Pearson's correlation coefficient to locate the optimal measurement nodes of the area frequency. Then, since the rate of change of frequency (RoCoF) index contains a lot of oscillating components, a numerical integration method based on a swing equation is proposed to estimate the area inertia and system global inertia. Finally, the modified IEEE 10-generator 39-bus system is established in DIgSILENT/PowerFactory to verify the effectiveness of the proposed method. The simulation results show that the proposed method is applicable for the equivalent inertia estimation of a power system with wind power in different scenarios.

low inertia; inertia estimation; area inertia; dispersion of frequency

10.19783/j.cnki.pspc.220472

国家自然科学基金项目资助(51977128)

This work is supported by the National Natural Science Foundation of China (No. 51977128).

2022-04-05；

2022-08-13

李东东(1976—)，男，博士，教授，博士生导师，研究方向为电力系统分析、新能源并网和智能用电；E-mail: psldd@163.com

董 楠(1997—)，女，硕士，研究方向为系统惯量评估；E-mail: d0ngnan2022@163.com

姚 寅(1986—)，男，通信作者，博士，讲师，研究方向为计及新能源与电动汽车的智能电网系统。E-mail: yin.yao@shiep.edu.cn

(编辑 魏小丽)