压缩加载条件下含水合物沉积物蠕变特性分析

李辉，张旭辉，陆程，谢鹏飞，鲁晓兵

1.中国科学院力学研究所，北京 100190

2.中国科学院大学，北京 100049

3.中国地质调查局油气资源调查中心，北京 100083

4.中国地质大学（北京）工程技术学院，北京 100083

天然气水合物（以下简称水合物）储量丰富，是最有可能代替化石燃料的清洁能源之一[1-3]。水合物沉积物层存在于低温、高压的自然环境中，陆地与海洋均有分布。中国海域水合物主要分布于南海地区[4]，据估算其储量约为6.4×1013m3，与中国常规天然气资源总量基本相当[5]，具有巨大的开发潜力。随着中国对于海域水合物研究的不断深入，中国地质调查局分别在2017 年和2020 年进行了海域水合物的试采[6-7]，实现短期稳定产气。

国内外学者针对含水合物沉积物的力学特性开展了丰富的力学试验研究[8-11]。Winters 等[12-13]通过核磁共振和三轴压缩试验分别对原状样品和人工合成样品进行测量，得到了水合物沉积物的强度和压缩波速。Masui 等[14]通过实验证实了原状样品和人工合成样品具有相似的力学强度，但是应力-应变关系随初始孔隙率和颗粒级配的变化而变化。Yun 等[15]通过室内试验证明了四氢呋喃水合物（THF）和甲烷水合物具有相似的力学强度，建议使用THF 进行力学性质研究。对于孔隙型水合物的研究较为广泛，Ren[16]等通过核磁共振发现水合物首先生长于小孔隙中，黏土会延缓整个生长过程。相较于均匀分布的含水合物沉积物样品，非均匀分布会对沉积物的物理和力学性质产生影响。Xie等[17-18]考虑了水合物沉积物的非均匀性，在人工样品中加入不同形状的水合物块体模拟不同的赋存形式，得到了不同形式下的水合物沉积物的强度和描述模型。含水合物沉积物的渗透率和破裂压力等均与水合物饱和度及分布形式有关[19-20]。然而大规模商业化开采水合物需要中长期稳定产气，因此还需要考虑储层的蠕变特性[21]。

目前，针对粉黏土蠕变特性的研究已经较为成熟[22-24]。余云燕等[25]针对非饱和盐渍土开展了一系列三轴固结不排水蠕变试验，在Singh-Mitchell 模型的基础上进行修正，提出了适合非饱和盐渍土的经验模型。罗庆姿等[26]通过三轴不排水压缩试验对汕头的软土进行了分析。Lai 等[27]针对三峡滑土带中的非饱和土进行三轴蠕变试验，引入了考虑基质吸力的相关参数，建立了适用于非饱和土的Singh-Mitchell 蠕变模型。刘业科等[28]通过梯级载荷加载方法进行室内三轴固结不排水的蠕变试验，在此基础上对Singh-Mitchell 模型进行修正使其能描述零应力零应变水平。关于常规粉黏土的蠕变特性试验已经开展了较多研究，积累了较多经验[29]。区别于常规软黏土的蠕变特性，含水合物粉质黏土在开采过程中存在水合物相变、渗流等过程，水合物分解前后沉积物的孔隙结构也相应发生改变，目前针对含水合物粉黏土的蠕变特性研究和相关模型的研究较少[30]。

本工作采用固结仪进行蠕变试验，研究了含水合物粉黏土的蠕变特性，并提出了描述模型。首先，通过试验获得了含水合物粉黏土的蠕变特性曲线，分析了含水合物粉黏土分解后的蠕变特性；在Singh-Mitchell 模型中引入水合物饱和度参数，构建并验证修正后的Singh-Mitchell 模型，得到了可以描述含水合物粉黏土的蠕变特性模型。

1 区域概况

研究区域位于中国南海北部的西北大陆边缘，呈NE 向延展，面积达4.5×104km2，具备稳定的高压低温环境，可以形成天然气水合物，也是我国重要的常规石油富集区域[31-32](图1)。试验采用研究区海域水合物储层的粉黏土沉积物，水合物赋存于海底7～158 m 范围内的第四系沉积物中，该区域平均水深约为1 000 m。

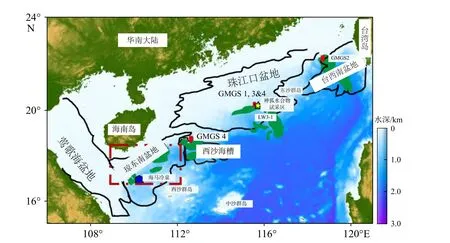
图1 研究区域位置[31]Fig.1 Location of the research area[31]

2 试验样品来源及方法

2.1 试验材料

土体的基本物理和力学性质如下：土体颗粒比重Gs=2.65，孔隙度n=0.509，平均粒径d50=0.0067，其中黏质组分（d≤4 μm）约占50%，砂质组分（4 μm＜d≤63 μm）约占45%，颗粒级配曲线如图2 所示。根据《土的工程分类标准》，试验用土粒径小于0.075 mm的颗粒质量分数大于50%，属于细粒土；不均匀系数Cu= 13.56，属于不均匀土，曲率系数Cc= 0.57，级配不连续。综上，试验土为级配不良的细粒土。

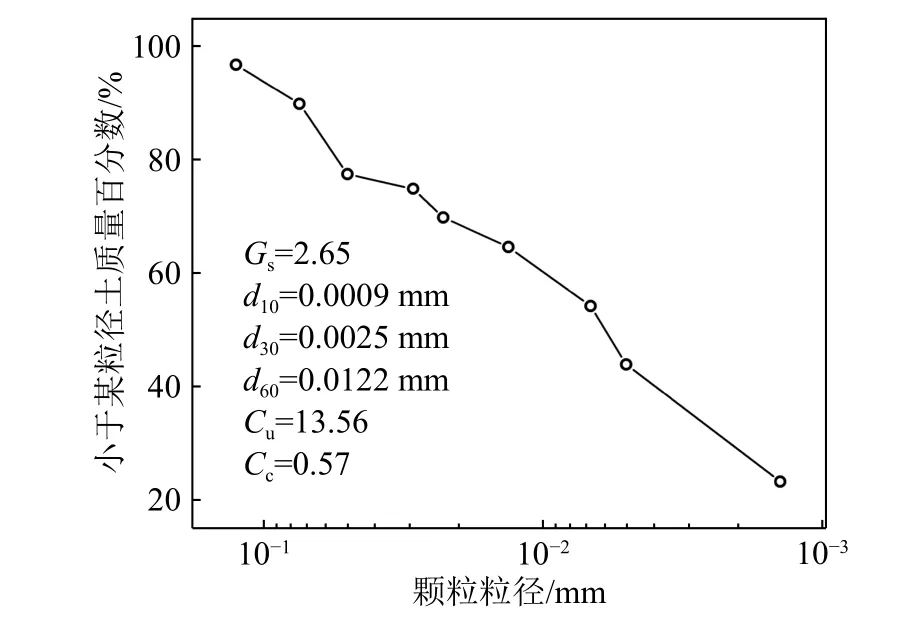
图2 沉积物颗粒级配曲线图Fig.2 Curves of sediment particle size distribution

试验所用的四氢呋喃溶液采购于中国国药试剂网，浓度为99.9%，通过加入蒸馏水配置成不同浓度的四氢呋喃溶液。质量分数为19%的四氢呋喃溶液在低温常压条件下可以完全合成四氢呋喃水合物，考虑到四氢呋喃的挥发性，试验中使用四氢呋喃溶液的质量分数为21%。根据试验样品所需的水合物饱和度，计算并配置一定质量分数的四氢呋喃溶液。

2.2 试验样品制备与试验设置

试验介质为粉黏土，基于试验区域水合物储层实际工况和土工试验结果，粉黏土比重Gs= 2.65，制备水合物沉积物样品时选取干密度 ρd=1.3 g/cm3，研究在恒定的上覆层荷载下水合物储层分解后对水合物储层的蠕变力学特性的影响。具体制备过程如下：

土骨架制备：将洗盐后的粉黏土沉积物置于烘箱中在105℃条件下烘干12 h 后取出冷却，研磨土体至颗粒完全粉碎（土体颗粒粒径小于0.2 mm）。根据干密度称取一定质量的沉积物平均二等分，将每份土体加入适量水后填入环刀内砸实至所要求的高度，在每层样品制备完成后将试样拉毛，以降低其分层的影响，制备成面积为30 cm2、高2 cm样品，置于烘箱中在105℃条件下烘干12 h 后取出冷却。

水合物合成：根据试验中水合物饱和度的设置配置不同浓度的四氢呋喃溶液，将制备好的土骨架置于密封罐内，密封罐与真空装置和储液装置相连，开启抽真空装置对样品抽取真空两小时，完成后通过储液装置自下而上浇注配置好的四氢呋喃溶液，保持密封状态一天至土样含液量稳定。最后取出浸泡完成的沉积物样品置于0～2 ℃的冷柜中1～2 d 合成水合物，如图3 所示。

图3 试验前后的试样Fig.3 Sample before and after test

在试验前取出含水合物沉积物样品置于密封罐内分解，从而得到不同水合物饱和度分解后的沉积物样品。采用分别加载的方式进行，在荷载的作用下，连续观测。加载应力分别为：①号0.5 MPa、②号2 MPa、③号3 MPa 条件下进行试验；分解前水合物饱和度分别为 0%、20%、60%、80%。试验仪器使用固结仪如图4，通过采用单杠杆固结仪试验获得水合物沉积物的蠕变力学响应参数。

图4 高压固结仪实物图Fig.4 High-pressure consolidation apparatus

高压固结仪放置于20℃的恒温室中，在试验过程中保持样品处于饱和状态，当沉降值稳定后样品停止变形，即认为试样的变形不超过0.001 mm/d 后达到稳定状态。

3 结果和分析

3.1 试验结果

通过对原始数据的整理，得到了分别加载方式下，不同水合物饱和度（SH）粉质黏土样品分解后在轴向压力σ下试验时间t和应变ε的蠕变试验曲线（图5）。

图5 不同饱和度下蠕变全过程曲线图Fig.5 The whole-process curve of creeping under different saturation degrees

由图5 中可以看出，在分别加载的条件下，含水合物沉积物分解后样品在各级荷载下的应变-时间关系曲线的变化规律基本相同，只有初始蠕变阶段和稳定蠕变阶段，并未出现加速蠕变阶段。施加荷载的初期，均产生了较大的瞬间变形，曲线呈飞跃式增长。随着时间的推移，曲线的斜率逐渐减小，表示试样的变形速率逐渐减小。最终，试样的变形速率趋于稳定，曲线呈斜率较小的直线，试样的变形随时间不断增大，但该阶段变形值较小。

含水合物粉质黏土样品的蠕变特性曲线可以分为瞬时变形、固结变形和蠕变变形3 个阶段[33]。水合物的赋存改变了粉黏土的初始孔隙结构，在施加荷载的瞬间会产生较大的变形进入瞬时变形阶段；当样品孔隙被压缩，孔隙水被排出，而由于黏土沉积物骨架的渗透率较低因此会产生超静孔隙水压力并需要较长时间消散，处于固结变形阶段；最后固结完成后，在恒定荷载的作用下，由于恒定轴向压力的作用，土体骨架持续变形，应变不断增加但总体应变率较小，最后趋于稳定，处于蠕变变形阶段（图6）。无水合物沉积物应变率和时间的曲线见图7。瞬时变形认为当轴向荷载加载完成后完成，取1 min 对应的应变作为瞬时变形。将图7中的转折点作为固结变形和蠕变变形分界点，即将应变率1×10-5/min 作为固结变形和蠕变变形分界点。

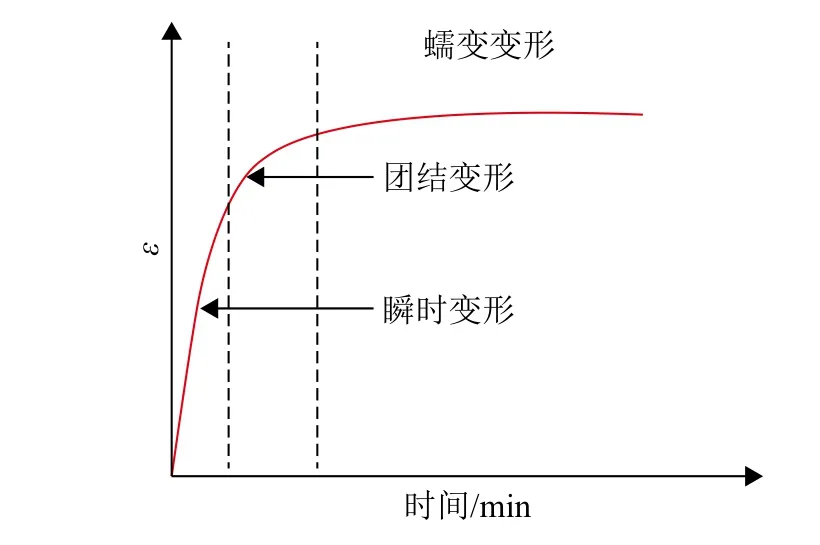
图6 变形过程三阶段示意图Fig.6 Diagram of three-stage deformation process

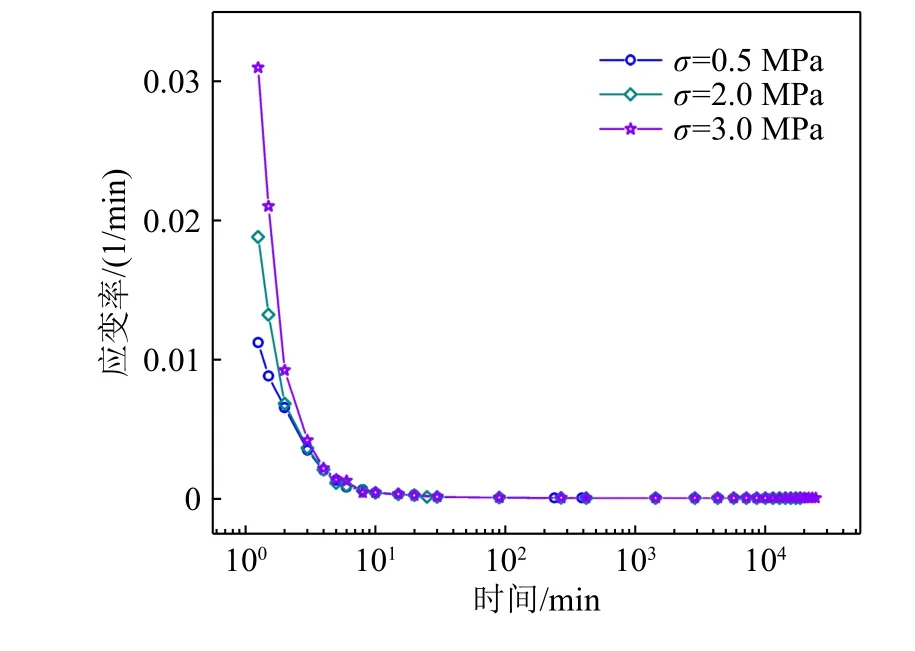
图7 无水合物沉积物应变率和时间的曲线Fig.7 Curves of strain rate and time for hydrate-free sediments

3.2 Singh-Mitchell 蠕变模型

Singh 和Mitchell 等[34]在总结大量土体蠕变的基础上，使用指数函数及幂函数的形式描述黏土的应力-应变-时间关系，并在此基础上提出了Singh-Mitchell 蠕变模型。Singh-Mitchell 蠕变模型具有参数少、适用范围广等特点，因此本文先择此模型来描述粉黏土的蠕变特性。Singh-Mitchell 蠕变模型可以表示为：

式(2)中 ε为轴向应变， ε0为初始轴向应变；在不 考 虑 初 始 的 轴 向 应 变 时， ε0=0 ，令 λ=1-m，，得到式(3)：

式(3)即蠕变方程，其中需要确定的参数有3 个分别为B、β、λ。

当t=t1时，有 ε=ε1，可以得到方程(4)，两边取对数得到方程(5)：

β和B的值可以直接通过单位参考时间t1的lnε-Dr直线关系图得到。土体的非线性蠕变是一簇曲线，从上式中可以看出Singh-Mitchell 蠕变模型也是一簇指数形式的曲线，形状与现有的粉黏土蠕变试验结果吻合，因此选择Singh-Mitchell 蠕变模型来描述粉黏土的蠕变特性是合适的。

3.3 试验用粉黏土蠕变特性分析

将蠕变特性曲线绘制在双对数坐标轴中，可以得到 lnε-lnt关系图（图8），图中可以看出，在不同的剪切应力水平下样品的蠕变试验曲线为一组平行近似的直线，直线的斜率为模型中 λ 值。将t1=1min时的应变带入式(4)和式(5)中得到 lnεr-Dr关系曲线，拟合后具有良好的线性关系，通过式(5)可以计算出不含水合物沉积物的β和B值（图9）。

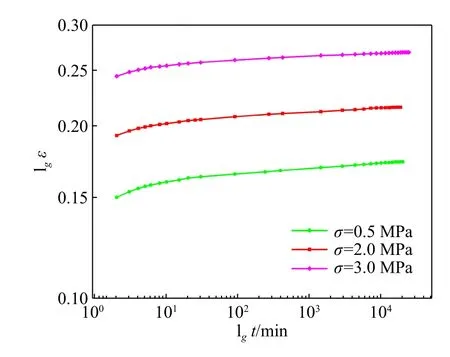
图8 无水合物试样 lgε vs lgt蠕变特性曲线Fig.8 The lgε vs lgt creep characteristic curve of hydrate-free samples

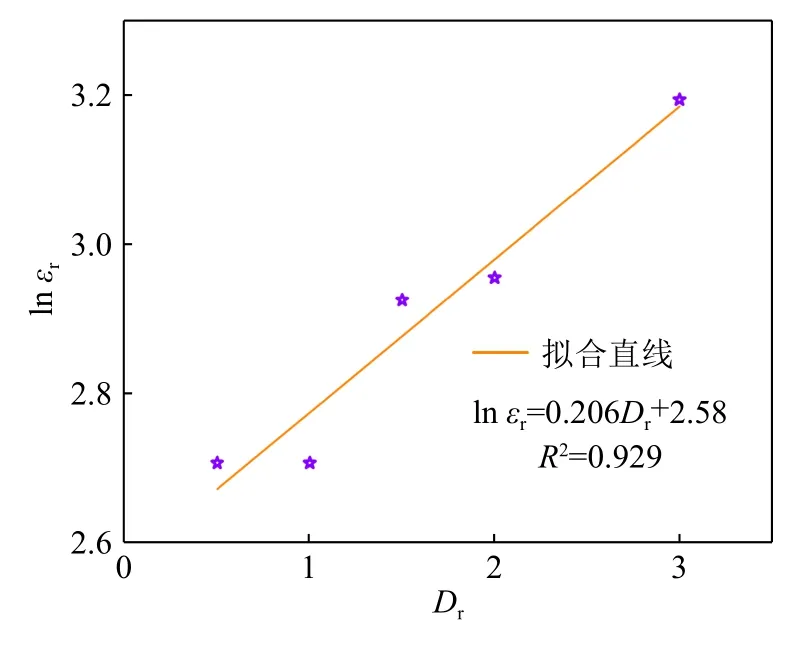
图9 lnεr vs Dr关系拟合曲线Fig.9 Fitting curve lnεr vs Dr relationship

考虑含水合物沉积物的剪切应力，偏应力的计算公式为q=(1-K0)*σ ， 其中K0为静止土压力系数，σ为轴向应力。根据Simpson 等[35]正常固结黏土K0经验公式：

将三轴剪切试验内摩擦角 φ′=5°带入式(6)后得到K0=0.84，即q=0.16σ，同时注意到不同围压下qf=0.15～0.2 MPa[36]，，因此后续取值Dr=σ。

带入上述参数计算Singh-Mitchell 蠕变模型中的相关参数值，结果如表1 所示。

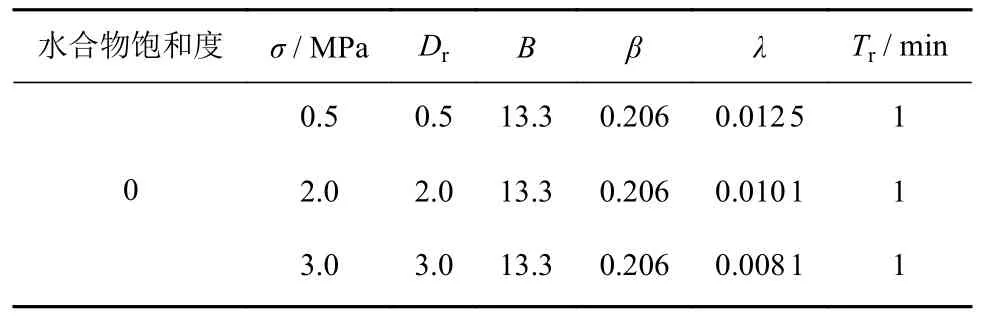
表1 Singh-Mitchell 蠕变模型中参数计算值Table 1 Parameter values of the Singh-Mitchell creeping model

将表1 中计算的模型参数带入式(4)中，以轴向压力σ为0.5 MPa 为例得到Singh-Mitchell 蠕变模型的表达式：

将模型计算曲线和试验值进行对比（图10）。可以看出，Singh-Mitchell 蠕变模型计算曲线和蠕变试验曲线的发展趋势具有较好的一致性，在加载瞬间应变快速增长，随着时间的增加轴向应变迅速衰减。在较高的剪切应力水平下Singh-Mitchell 蠕变模型和试验曲线具有较好的一致性，在较低的剪切应力水平下模型计算值略大于试验值，有一定的误差，总体拟合关系较好。

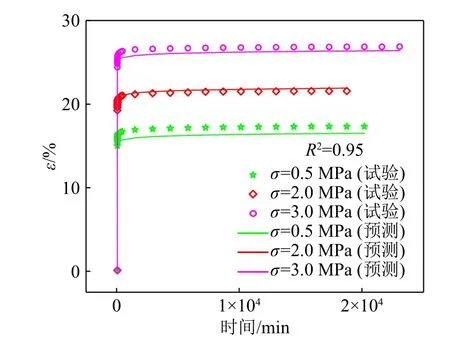
图10 无水合物模型计算曲线和试验值对比Fig.10 Comparison of model calculation curve to the test result of hydrate-free sediments

3.4 含水合物试样蠕变特性分析

上一节中讨论了不含水合物沉积物样品的蠕变特性曲线，通过结果可以看出Singh-Mitchell 蠕变模型可以描述其蠕变特性，为了使Singh-Mitchell 蠕变模型可以描述含水合物沉积物样品，需要对模型进行修正。引入水合物饱和度SH来描述水合物含量，SH是指水合物与孔隙体积之比[37]：

水合物在合成时会膨胀从而引起土体孔隙的变化，在经典模型中，模型参数A反映出土的组成、结构和应力历史等特性，因此考虑通过对参数A进行修正来表征水合物饱和度的影响，在Singh-Mitchell 蠕变模型的基础上引入模型如式(9)：

式中，α为模型参数，根据试验数据，本文中取0.37。

将修正后的参数A和不同水合物饱和度经典模型中的参数A进行对比（图11），可以看出其具有良好的对应关系。

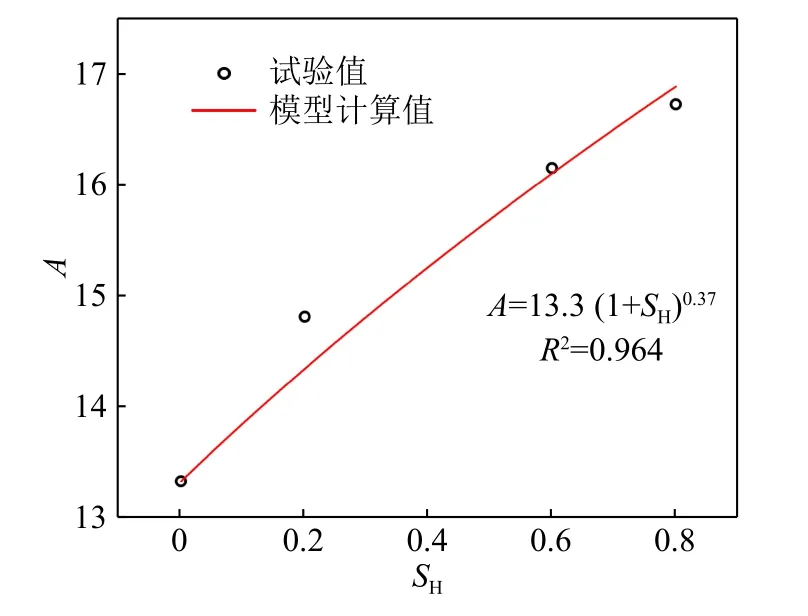
图11 经典模型和修正模型参数 A对比图Fig.11 Comparison of classical model and modified model parameter A

由此建立了一种修正的Singh-Mitchell 蠕变模型：

当SH=0 时，模型又退化成经典的Singh-Mitchell蠕变模型。

通过计算，得到不同工况下修正的Singh-Mitchell蠕变模型参数，得到参数（表2）。

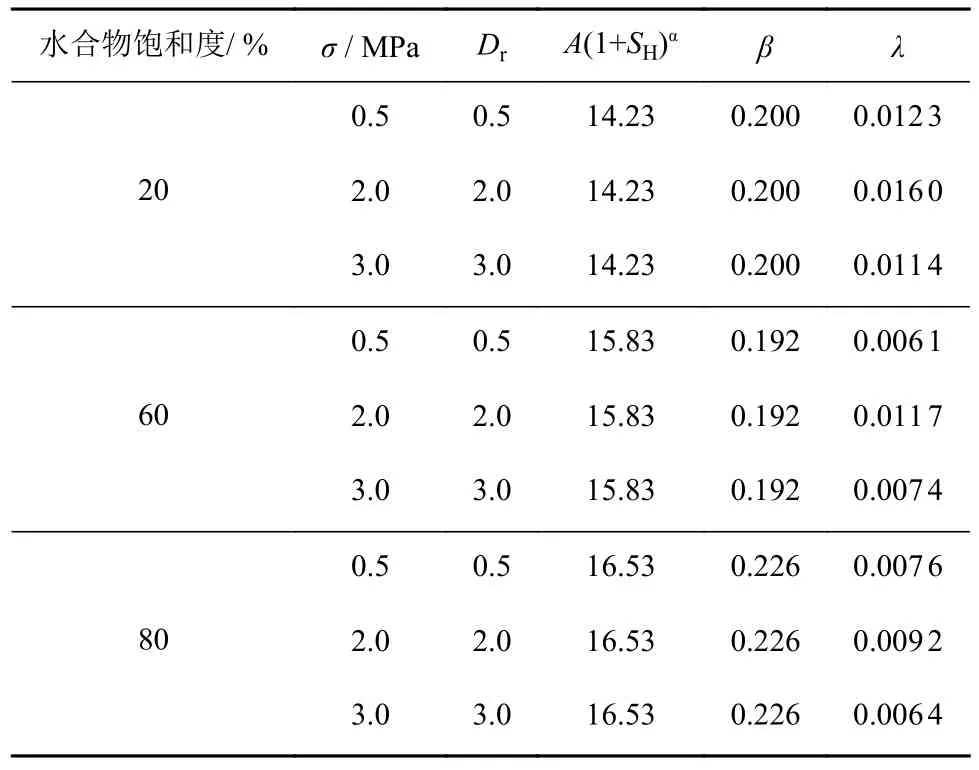
表2 修正的 Singh-Mitchell 蠕变模型参数值Table 2 Parameter values of modified Singh-Mitchell creeping model

将表2 中的参数带入公式(10)中，得到模型计算值，同时和试验数据对比如图12 所示。

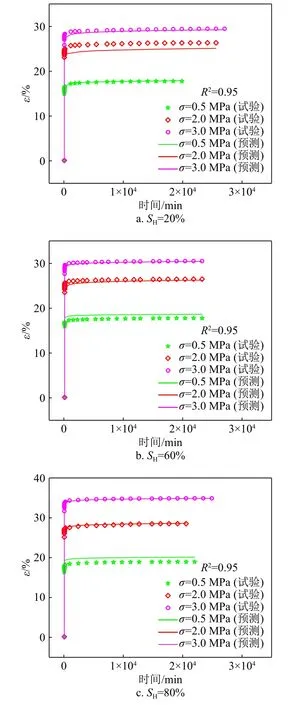
图12 不同水合物饱和度模型计算曲线和试验值对比Fig.12 Comparison of model calculated curves and the test values at different hydrate saturation degrees

从图12 可以看出，修正后的Singh-Mitchell 蠕变模型在不同水合物饱和度和剪切应力下都能够较好地预测均匀分布的含水合物粉质黏土样品的蠕变特性，因此可以使用此修正的Singh-Mitchell 蠕变模型来预测含水合物沉积物样品的蠕变特性曲线。修正的Singh-Mitchell 蠕变模型参数计算简便、参数较少并且容易获取，使用较为方便，因此本文建立的修正Singh-Mitchell 蠕变模型对描述含水合物沉积物样品的蠕变特性曲线更为合适，对我国南海水合物储层长期开采后的沉降预测具有一定的指导意义。

4 讨论

4.1 蠕变试验结果分析

南海海域水合物主要赋存于海底以下到200 m范围内的粉黏土等未固结的沉积物内，具有含水高、孔隙度高的特点，水合物饱和度最高可达90%以上[38]。因此本文根据储层的实际赋存条件，以水合物储层的粉黏土为介质，在0.5、2 和3 MPa 的压缩加载条件下进行了0、20%、60%、80%水合物饱和度分解后的蠕变特性试验。试验表明：加载过程中，含水合物沉积物经历瞬时变形、固结变形和蠕变变形3 个阶段；在加载的短时间内，瞬时变形阶段完成，引起的轴向变形约占总变形量的70%～80%，最大值为85.8%，在固结变形阶段，孔隙水在稳定的应力条件下从孔隙中排出，一般数小时内完成，引起的轴向应变占应变量的15%～25%，最后的蠕变变形阶段一般数天内完成，引起的轴向应变小于总应变量的5%。轴向压力和水合物饱和度均对轴向变形有影响。轴向压力越大，蠕变变形越大，轴向压力在较低水平时变化对轴向变形的影响大，随着轴向压力的增加，这种影响程度减小。水合物饱和度主要通过改变样品的微观孔隙结构进而影响蠕变特性，分解前的水合物饱和度越高，蠕变变形越大。水合物饱和度在低轴压条件下对变形影响小，在轴压为0.5 MPa 时，从无水合物到水合物饱和度增加到80%时，轴向变形从17.25%增加到18.8%，而在轴压为3 MPa 时，轴向变形从26.83%增加到了34.73%。

4.2 基于Singh-Mitchell 的修正模型

数学模型是定量描述各个试验变量之间相互关系的常用方法。之前的海洋地质调查海域水合物储层粉质黏土进行蠕变特性的研究不足，本文利用蠕变试验结果，通过建立修正的Singh-Mitchell 蠕变模型，对研究区域内水合物储层土的蠕变特性进行初步分析。从蠕变模型中可以看出，通过轴向压力和水合物饱和度两个物理指标能够建立出较好的蠕变模型，反映出这两个物理指标是蠕变特性的主要影响因素。模型中参数α和土体初始条件有关，主要根据试验获取，反映出土体的蠕变特性与土体孔隙微观结构、颗粒级配、应力历史等多种因素相关。

5 结论

（1）含水合物沉积物样品蠕变特性曲线可以分为瞬时变形、固结变形和蠕变变形3 个阶段。瞬时变形数分钟内完成，引起较大的变形，固结变形数小时内完成，引起较小的变形，蠕变变形数天内完成，引起极小的变形。

（2）蠕变变形随着加载应力水平、水合物饱和度的增大而增加，水合物饱和度主要通过改变沉积物样品的孔隙结构从而影响蠕变变形，水合物饱和度越高，孔隙结构受影响程度也越大，试样的物理和力学性质越差。在低应力水平时，水合物饱和度对蠕变变形的影响不明显。

（3）基于应力水平和水合物饱和度建立的修正Singh-Mitchell 蠕变模型，可以有效地预测含水合物沉积物的蠕变特性，对水合物储层长期开采后的沉降变形预测具有指导意义，便于实际工程中推广。但由于试验组数少等原因本文未对水合物沉积物蠕变变形机理进行深入研究，针对非均匀分布的含水合物沉积物蠕变特性也需要进一步研究。