超精密加工误差补偿技术研究综述

陈启迪 胡小龙 吝 敏 孙晓霞 张 涛 周志雄

1.中国北方车辆研究所，北京，100072 2.湖南大学机械与运载工程学院，长沙，410082

0 引言

随着科技的发展，超精密加工机床在国防安全、现代通信、航空航天等高端技术领域的需求快速增长。国内很多机床企业也能生产超精密加工机床，但核心部件仍需外购，在众多核心技术领域仍是空白。制约我国机床水平提高的因素一方面在基础科学方面，材料性能不达标、生产工艺不完善、结构设计不合理，使得生产出来的零部件性能达不到要求、可靠性差。另一方面在控制、测量技术方面，国内现有的机床运动、误差补偿模型和理论还不完善，软硬件系统功能性、兼容性、通用性差，传感器灵敏度低，测量装置精度低等，极大地限制了加工精度的提高。

目前，提高机床加工精度、减小机床误差的方法主要有两种：一是误差防止法，即通过改进机床的设计、制造和装配等工序来尽可能减少乃至消除误差[1]；二是误差补偿法，即通过对原始误差进行测量，并人为制造出其反向误差与之叠加进而抵消或削弱原始误差所造成的影响。机床误差补偿技术经过数十年的发展，经历了探索、发展与应用三个阶段，误差补偿理论与研究体系已经渐趋完善，但在超精密加工机床上的应用还不成熟，尤其是对于超精密微细加工，由于所加工零件尺寸微小、结构复杂，精度要求更高，针对超精密加工机床的旋转轴等关键部件的误差补偿研究依然是当今学术界和工业界的研究热点和亟需攻克的难点。因此，非常有必要阐明超精密加工误差补偿技术的内容范畴，全面分析超精密加工误差补偿技术研究现状，从中判断和把握存在的问题及发展趋势，推动我国超精密加工机床行业快速发展及生产应用，提升我国超精密加工制造水平。

1 机床误差源

机床精度的高低直接影响加工工件的表面质量。图1展示了20世纪以来机床加工精度的变化趋势，由图可知，机械加工按照精度等级可分为普通、精密以及超精密加工三个层次。随着科学技术的进步，机床精度也随之提高，精度等级也在不断跨越，目前，普通加工的加工精度已经达到了20世纪40年代超精密加工技术水平，超精密加工的加工精度已达0.01～1 μm、加工表面粗糙度达0.005～0.04 μm。但随着加工精度等级的提高，精度提高的难度在不断加大，精度提高的幅度呈放缓趋势。

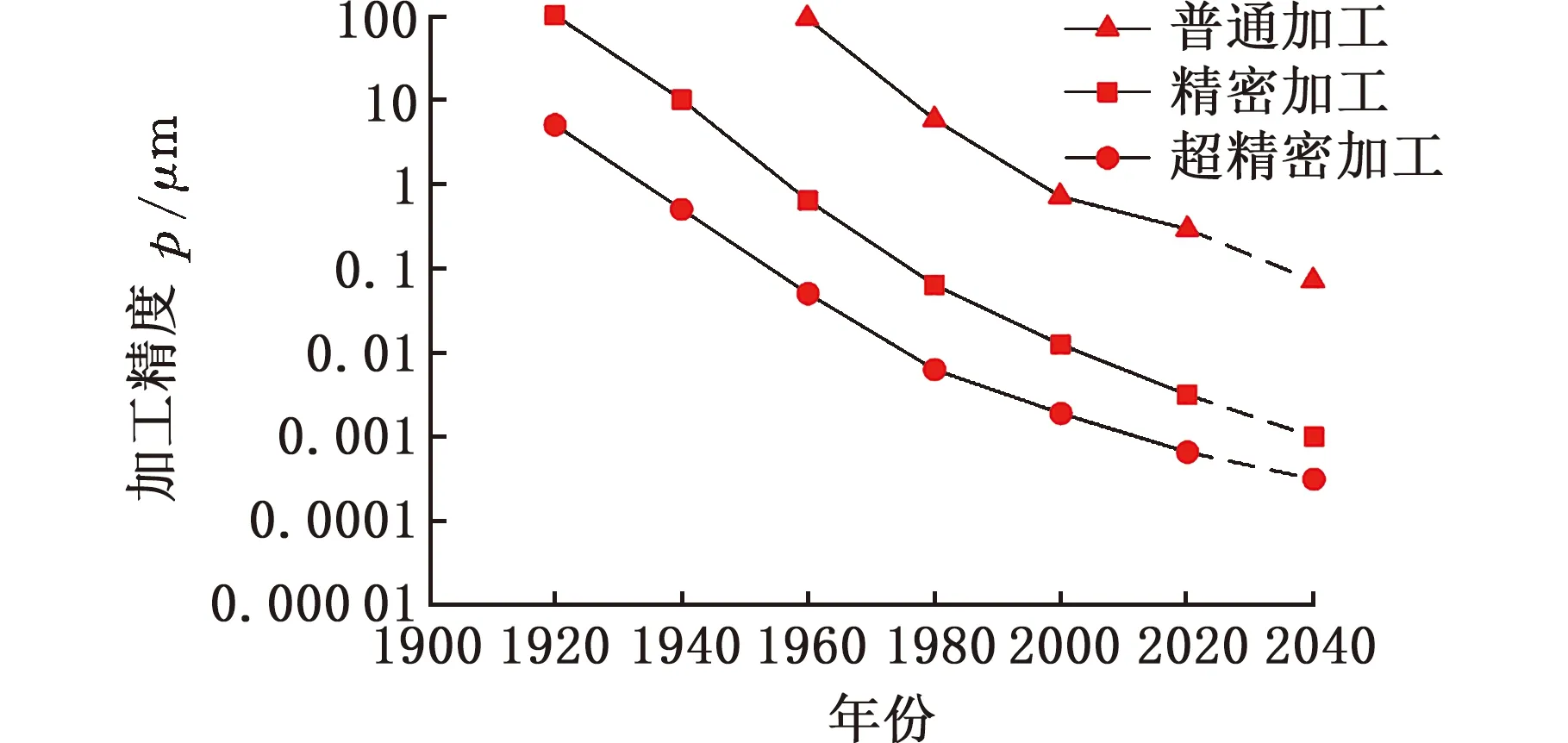
图1 加工精度的变化趋势

一个完整的机械加工工艺系统由“机床-刀具-夹具-工件”构成，工件的加工过程实际上是上述系统中各部件相互配合，进而实现位置移动和位姿变化精密控制的过程。然而，在实际加工中，诸多外界因素会导致各部件之间的运动不能完全按照理论状态运行，从而产生不同类型的加工误差，如：机床零部件设计、制造和装配缺陷导致位置偏移而引起的几何误差(geometric errors, GEs)，切削力导致工件、刀具、夹具之间发生力变形而引起的力诱导误差(force induced errors, FIEs)，加工区域以及周边环境温度变化导致机床热变形而引起的热诱导误差(thermal induced errors, TIEs)等。据统计，综合考虑不同机床自身的精度、损耗量、加工状况等因素，机床的几何误差、力诱导误差、热诱导误差分别约占机床总误差的18%、15%和35%。而对于超精密加工机床，通过配备机床恒温控制系统，并对环境进行严格的控制，极大地降低了热诱导误差对机床加工精度的影响。然而，超精密加工机床旋转轴的引入和微细刀具的使用使得机床对力诱导误差更加敏感[2-3]。因此，几何误差和力诱导误差成为影响超精密加工机床精度的主要因素。

根据误差性质不同，误差测量与补偿的方法也不同，如针对由装配导致的运动位置偏差，需要通过研究位置偏差与运动位置之间的关系来对其进行补偿；针对由切削力而导致的受力偏移或变形，需要通过研究切削力大小、机床刚度以及切削力误差之间的关系来对其进行补偿。因此，为便于对机床误差实施补偿，需要针对不同性质的误差进行相应的研究。图2列举了机床的主要误差源以及不同性质的误差产生的原因。

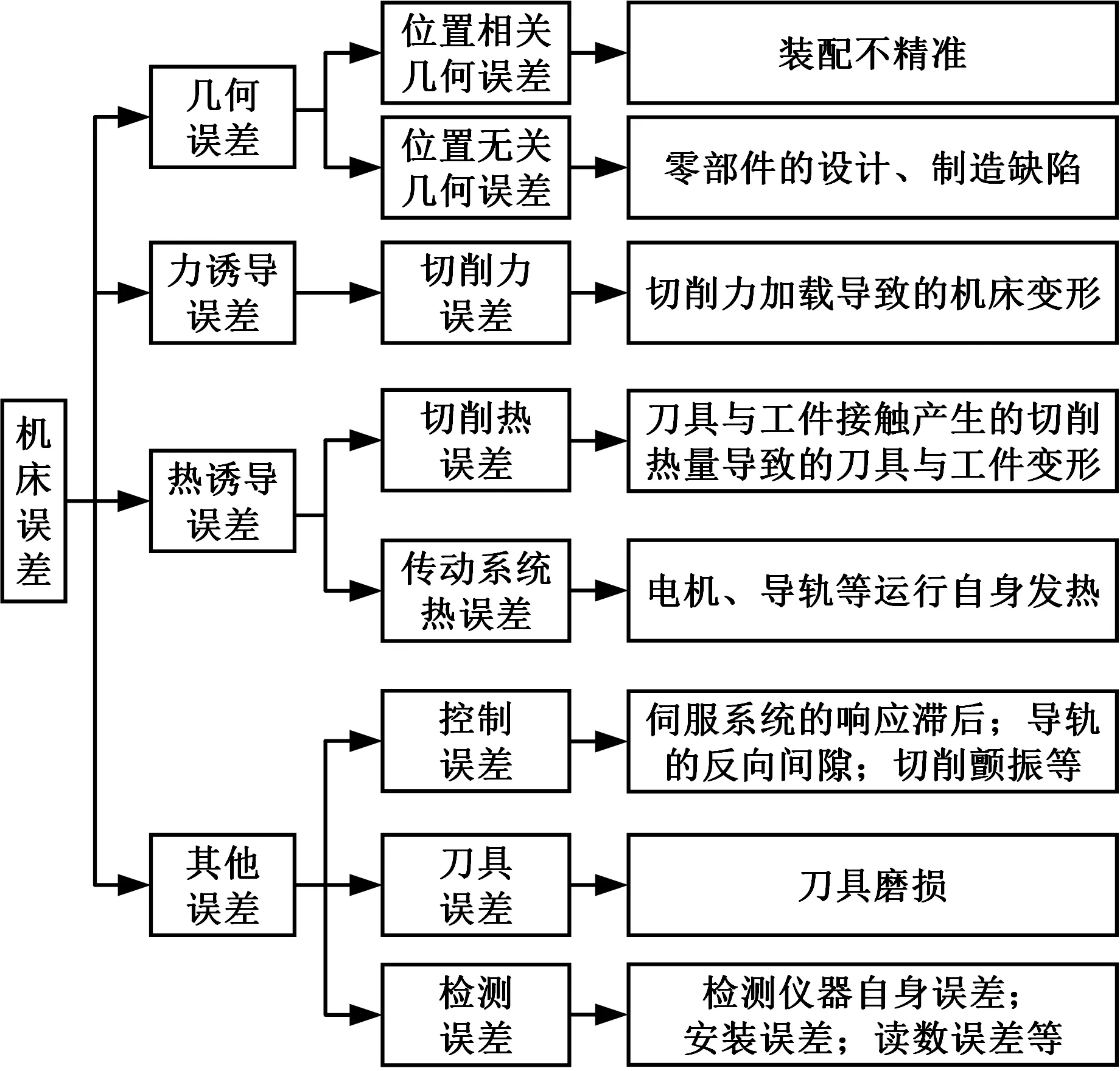
图2 机床主要误差源

随着加工精度的提高，机床的发展由简单到复杂，由单轴到多轴，各轴之间通过简单运动的相互配合实现不同形状的轮廓加工，机床的最终加工精度是由刀具与工件的相对位置共同决定的，机床在空间的实际轮廓误差是多种因素综合作用、各因素之间相互影响产生的结果，要确定两者之间的关系，需要建立完善的机床空间运动模型，并通过精确的测量来预测机床的位置移动以及空间误差。

2 超精密加工机床几何误差研究现状

根据ISO国际标准[4]的相关规定，机床的几何误差是指在标准测试环境(标准大气压及20 ℃恒定气温)中，机床处在稳定的运转及无负载状态下所产生的误差，该误差一般与机床各组成环节或零部件的几何要素有关，是机床本身固有的误差。超精密加工机床的几何误差可分为直线轴和旋转轴的GEs两部分，直线轴的几何误差补偿研究较为成熟，且模型通用性较强；而旋转轴的几何误差补偿研究还需要不断完善。

2.1 直线轴几何误差补偿

直线运动是机械加工中最基本的运动形式，因此，机床误差补偿的研究是从单个直线轴开始的。19世纪60年代，LEETE[5]提出对由数控机床导轨缺陷引起的直线轴GEs进行连续补偿的新概念，并提出使用光学测量的方法为误差补偿提供最佳的解决方案；FRENCH等[6]提出使用计算机编程对由工作台传动系统齿隙造成的直线轴加工误差进行补偿。数控机床误差补偿研究的开端从这一时期开始，随着研究的逐渐深入，业界对误差补偿的研究流程达成了共识，基本包括建立模型、测量参数和实施补偿三个步骤。其中，建立精确的误差模型是误差补偿研究最初也是最为重要的一步，将直接决定是否能够最终获得理想的误差补偿效果。因此，研究人员进行了大量误差建模方法的研究，其中，齐次坐标变换矩阵和刚体运动学理论得到了广泛运用。根据刚体运动学原理，采用齐次坐标变换的方法能够将空间误差表示为以位置、旋转、仰俯和偏转等误差分量为变量的综合表达式[7]。但由于不同运动状态对应的误差分量不同，故如何选取、确定参数，决定了误差补偿的计算效率。JUNG等[8]以刚体运动学为基础，通过多项式函数逼近误差分量，提出只需从4条对角线对14个测量点进行位置测量确定空间误差参数，可以提高误差补偿的效率。FAN等[9]通过研究齐次变换矩阵(homogenous transformation matrix,HTM)与运动链之间的内部关系，针对四种不同的三轴联动数控机床结构(图3)进行了误差分析与总结，并对其共性展开研究，建立了包含18个误差元素的统一误差模型。

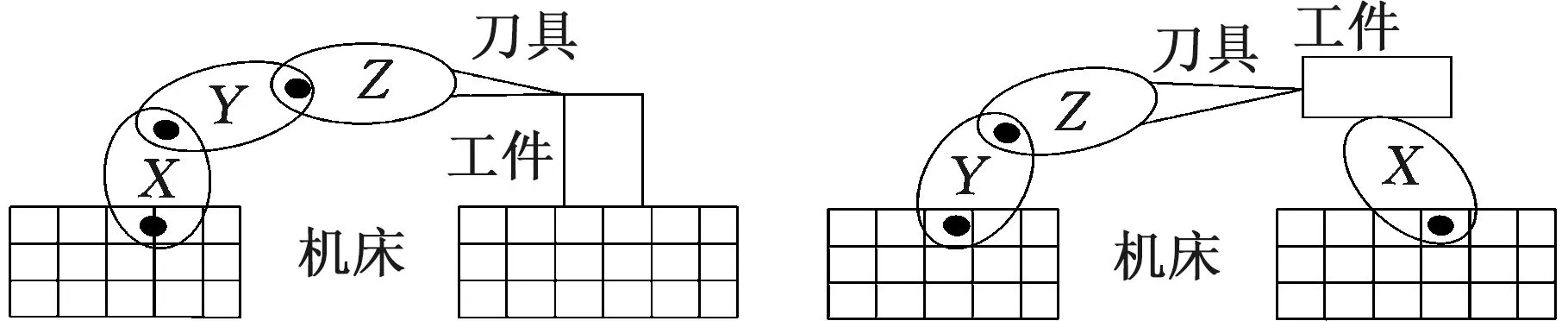
(a)TXYZ结构 (b)XTYZ结构

为进一步提高误差补偿的精度，误差补偿研究从单一地考虑运动轴的误差开始逐渐引入了其他的影响因素，进而产生了多种新的研究方法。FRANK等[10]首次提出使用微型计算机求解误差方程式的方法，从而进行机床的几何误差补偿研究，误差计算方法较为精确。YANG等[11]应用有限元法分析了机器人机构在给定输入运动或输入力作用下的动态和静态响应，但是由于使用有限元法需要获得精确的边界条件，其预测精度受到限制。HONG等[12]提出使用循环试验识别数控机床运动误差源的方法，将运动误差分为“无方向误差模式”(顺时针和逆时针测试信号的平均值)和“定向误差模式”(顺时针或逆时针测试信号与无方向误差模式的偏差)，并采用频率分析法和加权残差法对其分别进行识别，误差计算的精度进一步提高。MCHICHI等[13]使用接触式测量探头对安装在主轴上的标尺和标准球阵列(图4)进行测量，从而对超精密加工机床的位置误差和运动误差参数进行辨识，较为准确地界定各误差参量的影响机制。

图4 标准球阵列间接测量法[13]

误差补偿技术发展的最终目标是实现工业化应用，而实验室阶段的误差补偿研究还不具备大范围推广的能力，因此，通过误差补偿系统的开发，能够促进误差补偿技术在实际生产中的应用。DONMEZ等[14]设计了模块化误差补偿软件系统，对机床导轨的几何和热误差进行实时预测和补偿，取得了良好的误差补偿效果，可将机床精度提高20倍。2000年，密歇根大学联合波音公司，将误差补偿技术应用到飞机机翼加工的巨型龙门加工中心上，对其几何和热误差进行了综合补偿，成功将机翼的加工精度提高了10 倍，实现了数控机床误差补偿的工业化应用[15]。2004年，IBARAKI等[16]使用Kreuz Gitter Meßsystem in German(KGM)方法开发了一套数控机床运动误差测量和诊断系统，用于识别由机械结构和数控伺服控制系统引起的运动误差，误差补偿系统趋于成熟。

随着人工智能的发展，神经网络、深度学习等技术的运用越来越广泛，对误差补偿领域也产生了一定的影响。1993 年，东京大学提出 “智能制造”的新概念[17]，随后一系列智能建模方法被运用到机床误差补偿中，进一步提高了误差模型的预测精度[18]。1993年，密歇根大学安娜堡分校的吴贤铭制造研究中心通过对机床数控系统进行二次开发，开发了一套基于神经网络和计算机运行环境的加工误差实时补偿系统，进一步完善了误差补偿功能，实时补偿系统通过误差反馈及时调整加工参数，极大改善了加工质量[19]。次年，该系统被成功应用于100台车削加工中心上，取得了良好的批量误差补偿效果[20]，之后，密歇根大学与美国SMS公司进一步展开合作，开发了包括几何-切削力-热多误差综合补偿系统，并成功应用于一台双主轴数控车床上，多误差综合补偿使零件加工精度得到有效控制[21]。2008年，FINES等[22]开发出一套基于神经网络的误差补偿系统，并在两轴卧式机床上进行了实时误差补偿测试，神经网络通过寻优的方式使各误差综合影响程度降到最低。

目前，平动轴的几何误差补偿技术已经趋于成熟，根据本领域所达成的共识，研究者普遍认为各平动轴的平移误差、角度误差以及轴间垂直度误差共计21项，超精密加工机床的平动轴几何误差补偿与传统机床相同，平动轴的运动精度、稳定性已经达到了一个较高的水准。

2.2 旋转轴几何误差补偿

国外许多研究机构都非常重视超精密加工机床几何误差补偿功能的研究，目前，超精密加工机床误差的研究热点和难点主要在于其旋转轴部分，针对超精密加工机床的误差补偿研究，需要从机床结构出发，对旋转轴部分的静力学、动力学性能等方面进行全面分析。

20世纪90年代初期，SOONS等[23]基于三轴机床误差补偿研究，结合五轴超精密加工机床的特点，将旋转轴引入刚体运动学模型中。1993年，LIN等[24]引入了“固定误差参考系”和“运动误差参考系”的概念，并基于此提出了一种空间误差直接分析方法(D-H法)，用于评价超精密加工机床的位置和方向误差。之后，WANG等[25]、LAMIKIZ等[26]和LIN等[27]又进一步完善了D-H模型，并将其应用在机床定位误差的研究中。FLORUSSEN等[28]针对超精密加工机床结构的多样性，提出了一种基于体积三维长度测量的通用机床GEs误差补偿模型，使用该模型可以大幅提高误差补偿效率，从而降低误差测量成本，但其不足之处是测量设备价格十分昂贵，约为激光干涉仪的5倍。

ABBASZADEH等[29]根据机床的几何误差特性，将运动副准静态误差中的几何误差分为两大类：一类是与运动副运动位置无关的误差项(position independent geometric error parameters, PIGEP)，PIGEP是机床在整个运动过程中移动轴实际平均线偏离理想平均线的位置和角度误差，它们是由机床装配缺陷引起的，在机床的运动过程中固定不变；另一类是与运动副运动位置相关的误差项(positional dependent geometric error parameters, PDGEP)，用于描述在指定坐标系下运动副实际运动偏离理想运动造成的偏差，它是由机床零部件的缺陷导致的，随机床的位置实时变化。之后，位置无关几何误差(positional independent geometric errors, PIGEs)和位置相关几何误差(positional dependent geometric errors, PDGEs)(图5)被列入ISO机床精度评定国际标准[30]。

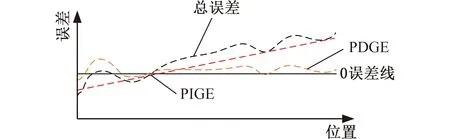
图5 几何误差关系

由于PIGEs误差元素相对于机床位置固定不变，而PDGEs误差元素随着机床的运动而改变，故PIGEs相对于PDGEs要易于补偿[31]，并且在大多数情况下，PIGEs远大于PDGEs，所以对PIGEs的误差研究往往不考虑PDGEs的影响。目前针对超精密加工机床旋转轴PIGEs补偿的研究相对较多。BRINGMANN等[32]提出了基于跟踪球的一次装夹误差测量法(图6a)，并成功应用于双转台五轴超精密加工机床所有PIGEs的测量，同时使用Monte Carlo模拟法对测量参数的不确定性进行了分析和建模，定性表征了误差偏离程度。GIVI等[33]通过对超精密加工机床各运动轴不同运动指令进行组合，实施了一系列简单的二维铣削实验，从而将机床误差信息“记录”于试件上，并使用触发式探头对铣削加工形貌进行机上测量(图6b)，来求解机床的PIGEs，但精度较低。MAENG等[34]在不考虑PDGEs的情况下研究了五轴超精密加工机床的旋转轴-刀具系统的10项PIGEs，如图7所示。

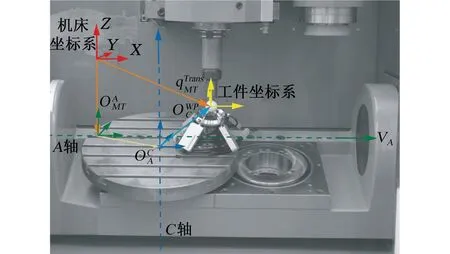
(a)基于跟踪球的测量法[32]

(a)旋转轴PIGEs

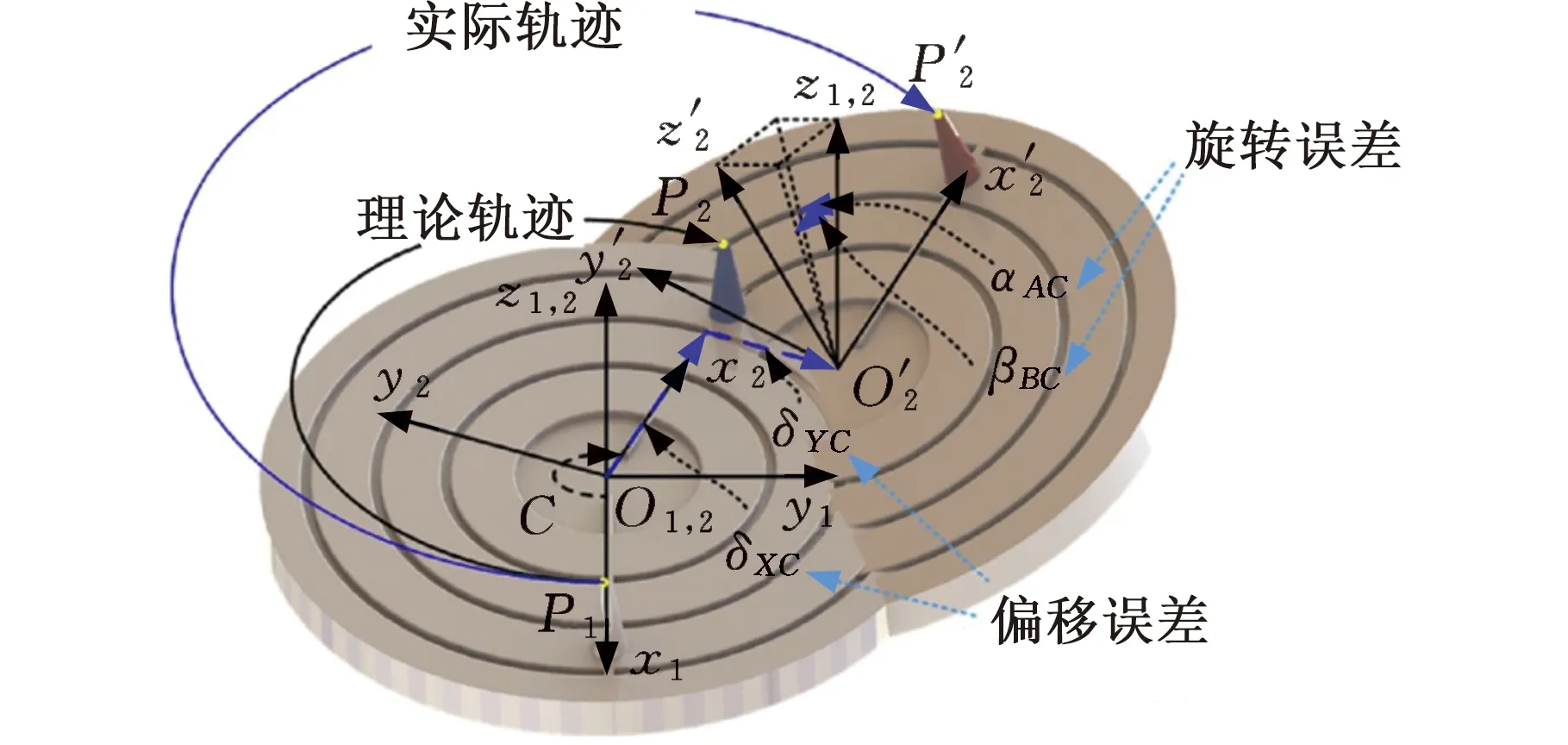
不同研究人员对误差的理解不同，误差建模方法也不尽相同，随着误差模型的增加，GEs的各种定义变得模糊不清，因此亟需对误差建模理论进行系统性的归纳总结。HUANG等[35]通过量化误差分量，将GEs分为“旋转轴分量偏移误差”和“旋转轴直线偏移误差”两类(图8a)，使GEs的识别和补偿更加有效。DING等[36]基于Huang等的研究，又提出了“误差优先”和“运动优先”两种误差建模思路(图8b)，用于根据计算执行顺序识别GEs的偏微分方程，但难以准确表征运动与误差之间的关系。GIVI等[37]针对超精密加工机床，提出“误差相关性”和“误差可补偿性”两个新概念，来解决误差补偿时可能存在的过度修正和工件表面质量退化等问题。

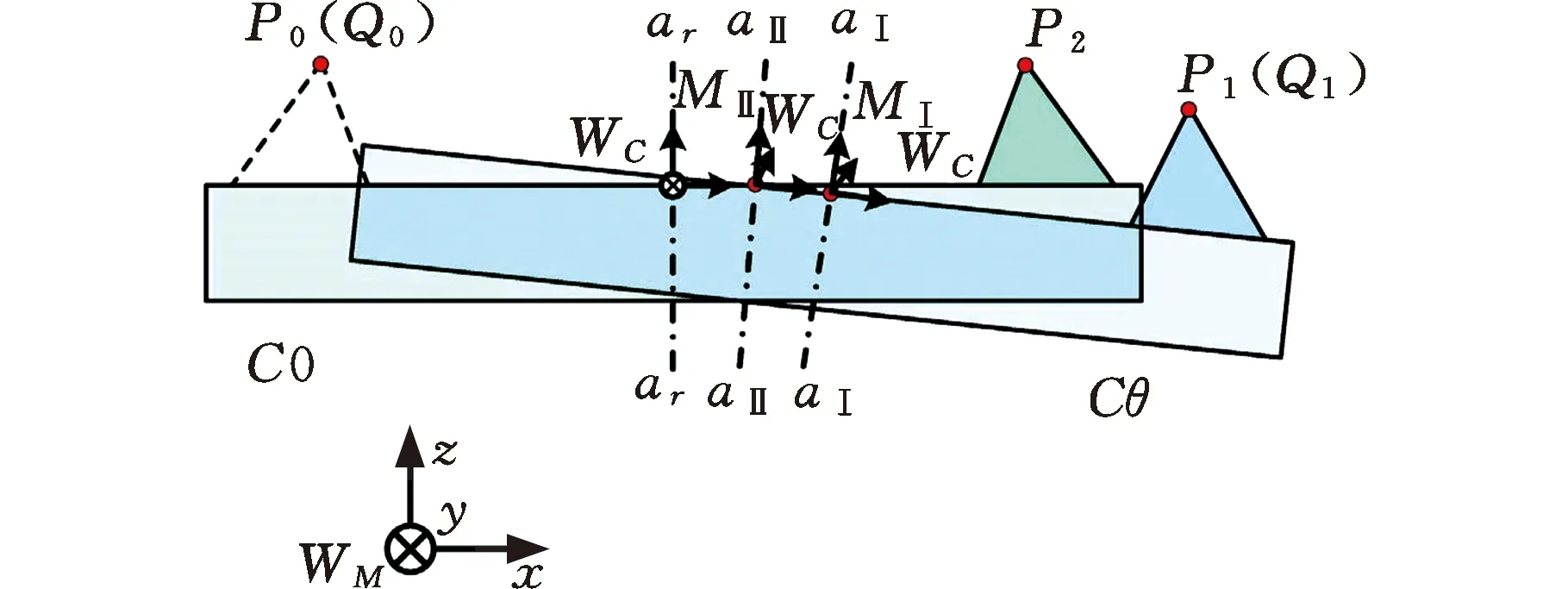
(a)“分量偏移”与“直线偏移”[35]

由于旋转轴的PDGEs识别比PIGEs识别更为复杂，需要更精密的测量设备、更复杂的测量步骤和大量的测量数据[38]，并且测量设备的反复安装调试也会引入更多的误差，这势必会降低误差补偿的最终加工精度，故在不考虑旋转轴PDGEs的情况下直接进行PIGEs误差补偿可以在一定程度上提高误差补偿效率。但是就超精密加工而言，由于加工精度要求较高，任何微小的误差都会比传统加工的影响更大，为进一步提高超精密加工机床的加工精度，有必要对旋转轴的PDGEs进行测量和补偿[39]。HONG等[40]分析了圆锥台加工圆度对PDGEs的敏感性(图9)，并讨论了旋转轴PDGEs对圆锥台加工精度的影响。XIANG等[41]对五轴超精密加工机床全部的41个PIGEs和PDGEs进行了测量和补偿，该研究在PIGEs和PDGEs分离的过程中，首先在假设PDGEs不存在的基础上对PIGEs进行测量，然后对PDGEs进行计算，最后通过反复迭代的方式实现PIGEs与PDGEs的分离，但迭代过程不易收敛。虽然PDGEs的研究已经取得了一定的进展，但大多数方法是基于传统的误差建模、测量和补偿思路，仍然难以准确有效地对PIGEs和PDGEs进行识别和分离。由于PIGEs和PDGEs产生的原因不同，而它们之间又相互耦合[42]，要实现PIGEs和PDGEs的完全分离，并获得PDGEs的连续精确值，需要大量的测量数据以及强大的计算能力。此外，除了进行实验验证，目前并没有统一的标准来判断PIGEs和PDGEs分离结果是否准确，这就导致误差分离存在很大的偶然性。

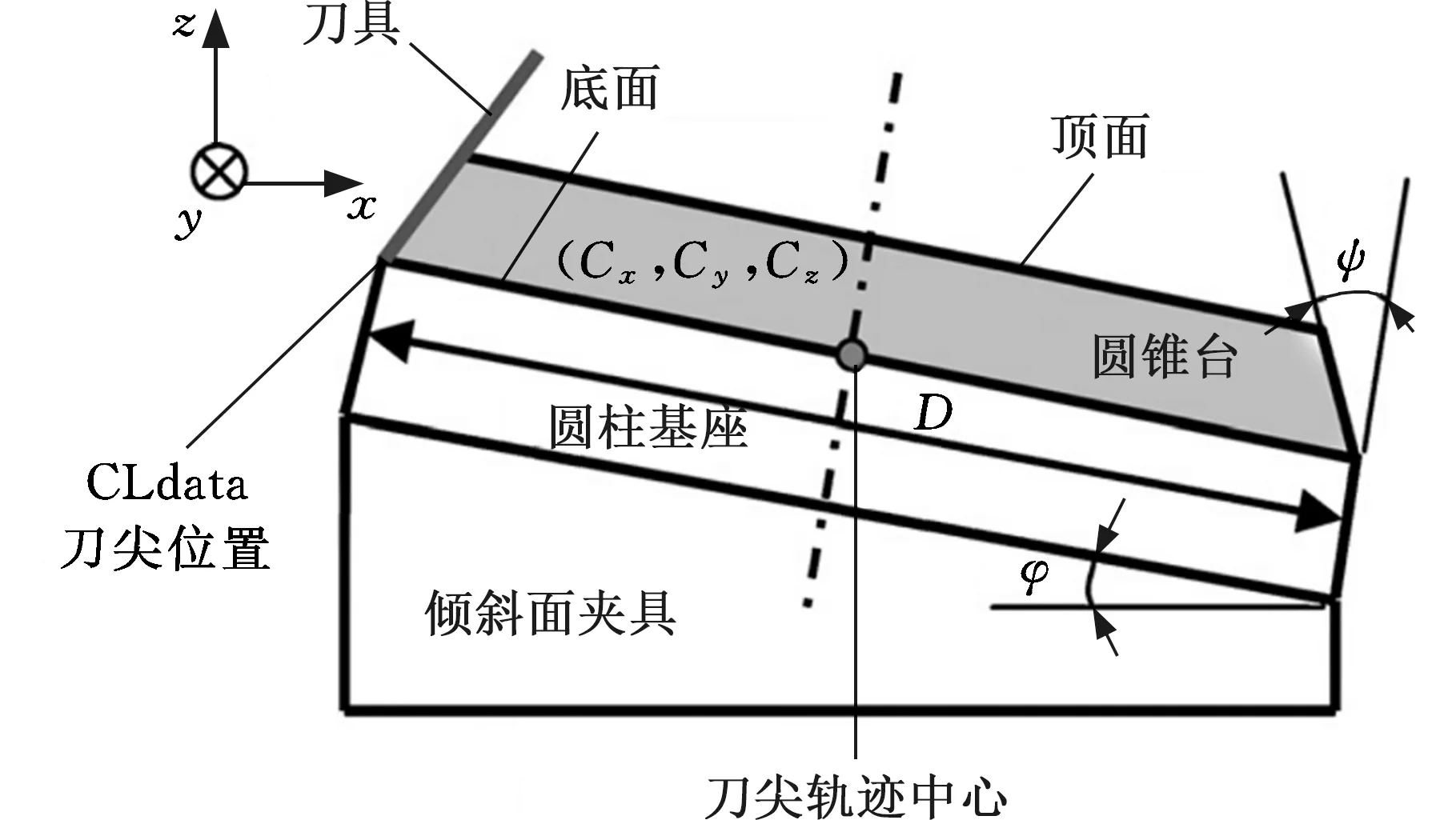
图9 圆锥台加工测量设置[40]

目前，针对GEs研究的各种测量设备也非常丰富，如双球杆仪(double ball bar)、触发式测头(touch trigger probe)、扫描式测头(scanning probe)、接触式跟踪球(chase-the-ball, R-test)、非接触式跟踪球(non-contact R-test)、三坐标测量仪(coordinate measuring machine, CMM)、激光跟踪仪(laser tracker)和激光干涉仪(laser interferometer)等多种专用仪器[43-47]相继被开发出来(图10)，在误差的精确测量中起到了关键性的作用。1982年，美国国家实验室的BRYAN[48]发明了磁力球杆仪(magnetic ball bar)，可以对机床轮廓进行精密的测量，该仪器测量方法简单，信息量大，现已被美国机床验收标准 ASMEB5.54和国际标准 ISO230-2收录，并得到了广泛的推广应用。国内外研究团队先后使用双球杆仪[49]、电荷耦合器(charge coupled device, CCD)工业相机[50]、跟踪干涉仪[51]、触发式探头、激光位移传感器[52]、在线激光测量仪、非接触式激光光障系统等多种仪器，并结合不同的误差补偿方法对超精密加工机床的GEs进行了建模、测量与补偿。

(a)VOP40P接触式测量[44] (b)CONTURA三坐标测量仪[45]

近年来，国内对机床GEs的误差建模、辨识与补偿也进行了许多相关的研究。杨建国等[53]在对五轴机床误差原理进行分析的基础上，结合坐标变换理论，建立了包含57 项几何和热误差的综合误差模型，并得到了广泛应用。沈金华[54]基于体对角线测量方法，对五轴超精密加工机床的空间误差进行了测量与补偿，拓展了误差测量方法。洪迈生等[55]提出一组由指令圆、控制圆、执行圆构成的误差分析方法来进行GEs的辨识与补偿，辨识度高，为误差高精度补偿奠定基础。范晋伟等[56]针对三坐标机床，以多体系统运动学理论为基础，建立机床误差源参数辨识模型，对22线测量法加以改进，提出14线位移测量法，对误差元素进行求解，测量效率更高，其误差补偿技术应用在多种数控机床上，取得了一系列研究成果。华中科技大学先后在激光球杆误差测量、多轴机床误差建模等方面进行了深入研究，并在多种数控机床上取得了明显的补偿效果[57]。

3 超精密加工力诱导误差研究现状

3.1 超精密加工机床力诱导误差研究背景

在精密超精密加工中，研究人员起初认为由于切削用量较小，加工相对平稳，所产生的力诱导误差FIEs可忽略不计[58]。但随着精度要求的不断提高，切削力对超精密加工精度的影响日益凸显，以往被忽视的FIEs重新成为研究热点，其原因如下。

(1)干切削加工技术的应用日益广泛。干切削加工技术是一种在加工过程中不用或使用微量切削液进行冷却润滑的绿色环保型加工技术，但是，干切削在加工硬脆材料时切削力较大，其影响不可忽略。

(2)以切代磨已成为切削加工的发展趋势之一。切削加工代替磨削加工作为工件加工的最后一道精加工工序，可以提高生产效率，但这也对机床和刀具的性能提出了更高的要求。

(3)高速、高效加工技术的发展。切削加工效率的上升伴随着切削速度、切削深度、进给量等参数的提高，在相同的时间内，获得更大的材料去除量势必需要更大的能量，这无疑会增大切削力的幅值。

(4)新兴材料的涌现。近年来，随着工业、科技的全面发展，各种新兴材料尤其是难加工材料的应用日益广泛，对加工性能的要求越来越高。

(5)单件、小批量生产对加工精度的要求提高。在传统加工中，工件加工以大批量生产为主，对于同批次的工件，在全测量范围内和相同加工条件下，切削力误差相同，属于重复性误差，一般可以被忽略。但现代加工中，个性化定制的单件、小批量生产越来越多，一台机床需要对多种零件进行加工，不同的加工条件会导致切削力误差不同，因而切削力误差不可被视为重复性误差而被忽略。

(6)随着加工技术的不断发展，机床制造水平越来越高。目前，世界上最先进的机床分辨率可达0.1 nm，在如此超高精度要求下，切削力误差不可忽略。

3.2 机床切削力模型

对于机床FIEs的研究，首先需要对切削机理有深入理解，并根据切削力与误差之间的关系建立切削力误差模型，然后对切削力进行准确的测量。ZHOU等[59]推导了塑性金属切削加工中剪切角的理论公式，建立了剪切力模型，并由此确定了切削力和切削参数之间的关系。JAYARAM等[60]基于大量的实际加工切削力数据建立了径向和切向切削力模型(图11)，并通过傅里叶变换预测单位切削力的大致范围。

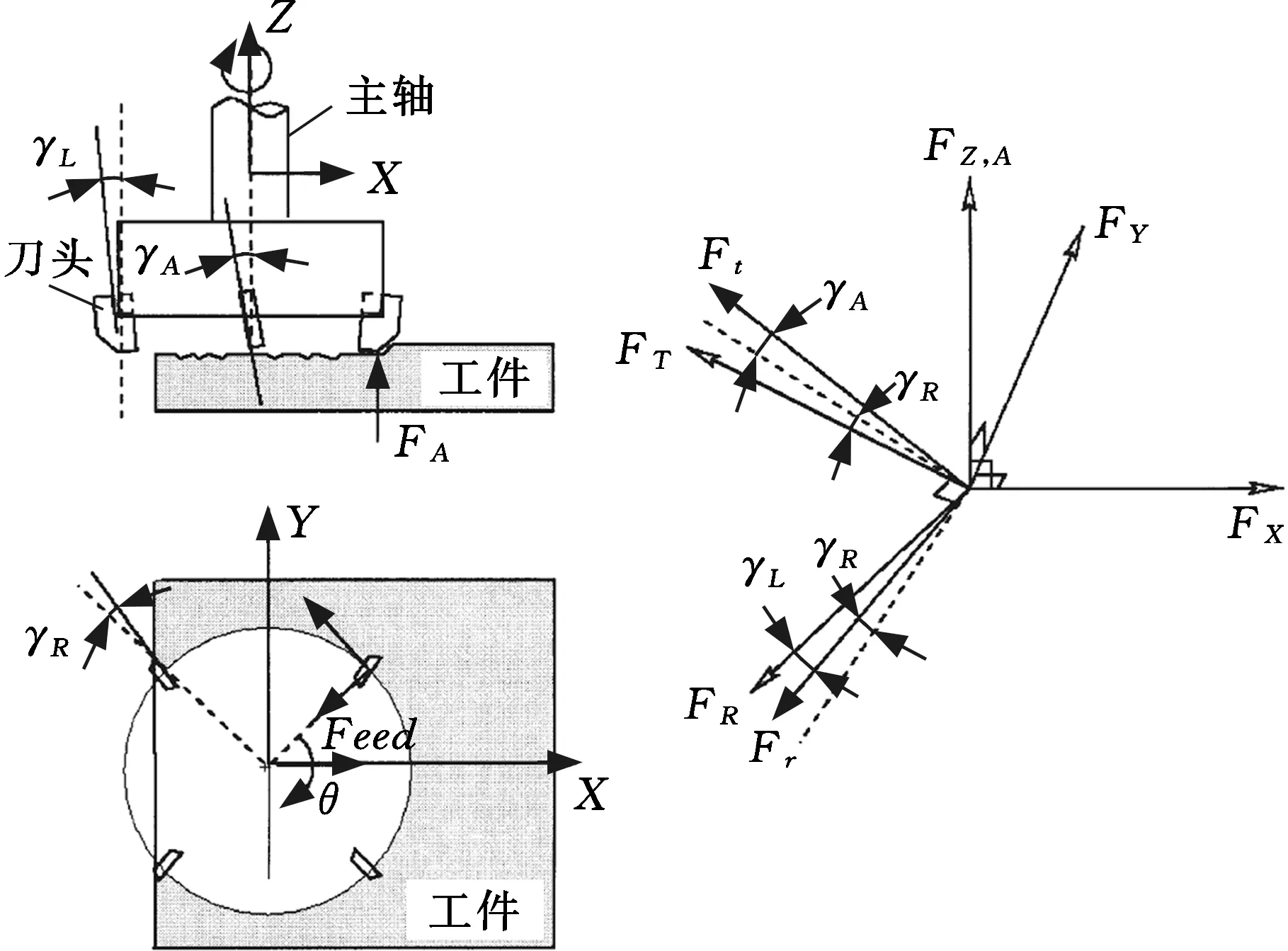
图11 铣削加工切削力模型[60]

超精密微细加工的特征尺度通常在10 μm～1 mm范围内，超精密微细加工用微刀具尺寸在0.1～1 mm范围内。相比传统加工技术，超精密微细加工在尺度上急剧减小，导致其表现出的加工机理特性与传统加工存在明显差异，例如微尺寸效应、刀刃钝圆半径和最小切削厚度等，而微细加工机理的不同会导致传统的切削力模型不再适用于微细加工过程。此外，通过建立切削力模型来预测切削力的方法需要综合考虑切削过程中的刀具形状、工件材料、切削条件以及加工参数等多种因素，从而对切削加工机制进行深入的分析。CHEN等[61]建立了微细铣削力模型(图12)，并考虑铣削力系数变化、切削阻尼等因素，对微细铣削加工三维稳定性展开了研究。但由于微细加工机理较为复杂，目前的微切削力模型仍有较大的改善空间。

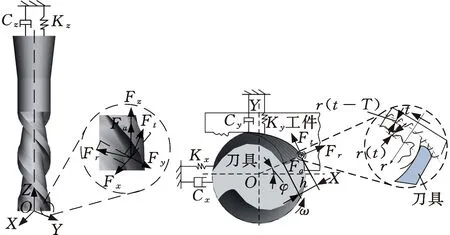
图12 微细铣削加工三维切削力模型[61]

在加工过程中，只有充分掌握切削力的实时变化状况，才能够精确地预测切削力误差、刀具磨损等与之相关的机床信息[62]。SPIEWAK等[63]在一台三轴机床上研究了主轴加速度与受力变形之间的关系，并基于此研制出一种切削力间接测量装置。SHIRAISH 等[64]使用位移传感器来预测切削力的变化，但由于位移传感器等测量装置需要固定在机床上，会对机床本身的加工精度产生一定的影响。KIM等[65]将实验测量和经验公式计算相结合，提出了通过制定切削力图来预测切削力变化的方法，但该方法只适用于标准零件的生产加工。为实现切削力的精确测量，KIM等[66]设计并开发了柱形电容式位移传感器(cylindrical capacitive displacement sensor, CCDS)，通过提取并分析切削力引起的主轴变形信号来精确标定切削力，测量误差小，但高频动态时的响应不足。于是GIRARDIN等[67]针对切削力测量时传统压电式测力仪在静态及高频动态时的响应不足、失真等问题，定义了基于切削参数的带宽标准，进而实现了切削力测量结果的精确校正。SCIPPA等[68]针对传统测力仪抗噪性、频率容限不足的缺陷，根据卡尔曼滤波原理，提出了一种测力仪测量结果补偿方案，提高了切削力的测量精度。

随着信号处理和测量技术的发展，研究发现切削力与机床驱动电机的实时输出功率有着密切的关系，许多专家学者开始利用数控机床电机电流信号来获取力信号。STEIN等[69]通过监测机床直流电机的电流变化来预测切削力的实时变化状况，该方法无需在机床上安装测量装置，因此测量过程不会对主轴系统产生干扰。ALTINTAS等[70]通过对进给系统电机的电枢电流进行研究，得到了切削力的变化信号，并通过对测力仪进行升级改造，提高了测力仪的带宽频率。LEE等[71]运用神经网络技术建立了主轴电机电流与切削力之间的关系模型，实现了基于神经网络的切削力误差建模。2003年，JEONG等[72]利用驱动电流进行频谱分析，设计开发了刀具损耗状况监测系统，并通过一系列实验研究，建立了固定式步进电机的电流与切削力之间的关系，将电流预测的切削力误差控制在15%以下。国内从2000年开始，陆续开展了数控机床切削力误差与电流关系的相关研究工作。吴昊等[73]通过研究主轴电流与切削力之间的关系，建立了三轴铣床主轴切削力误差模型，并进行了机床主轴切削力误差补偿实验，研发了一种可以弥补单一系统缺点的新型混合系统，解决了以往凭借单一系统难以解决的切削力误差问题。陈智俊[74]通过对切削力所引起的变形结果进行分析，采用霍尔电流传感器实现了对切削力的间接测量(图13)。吴昊等[75]基于电流测量对数控机床切削力误差进行了实时补偿，克服了以往利用传统的测力仪测量切削力耗时长、调试难、经济成本高等缺点，具有较大的工程应用价值。由此可见通过信号处理的方式，有效地降低了切削力误差。

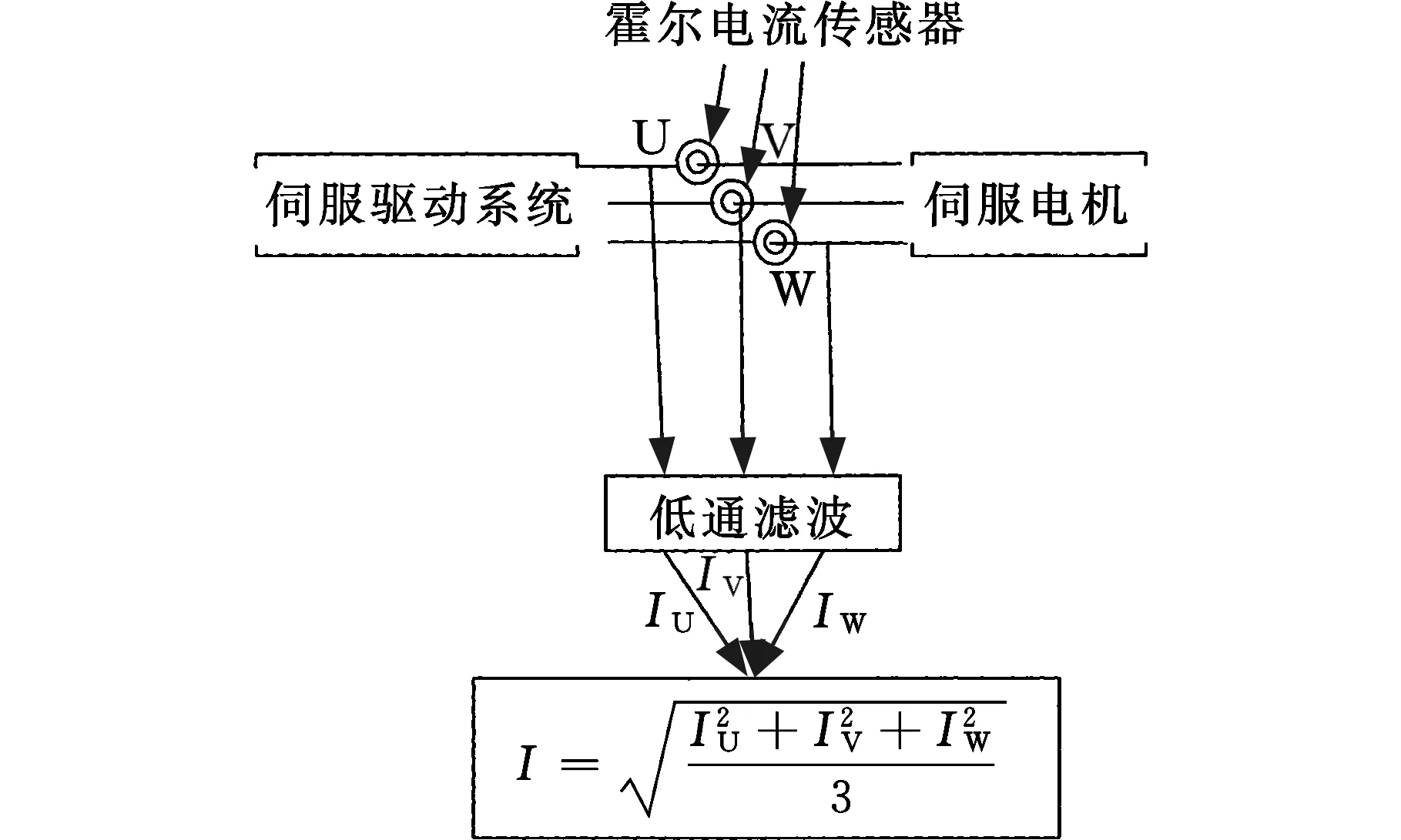
(a)原理图

3.3 超精密加工机床力诱导误差补偿

超精密加工机床不仅结构紧凑，而且用于精密加工的微细刀具尺寸(<1 mm)也比常规刀具小，从而使得机床旋转轴和微刀具的刚度要比传统机床小很多[76]。在超精密加工的尺度和精度要求下，切削力会使机床和刀具发生相对较大的变形，这种状况在加工硬质材料时尤为明显[77]。此外，机床零部件的自身质量也会在一定程度上影响超精密加工的精度[78]。HUANG等[79]设计了3自由度精密移动工作台(图14)，并在此工作台上做了负载分析，研究表明当负载大小为1 N时，其X方向最大变形量为17.83 μm，Y方向最大变形量为17.58 μm，Z方向最大变形量为11.43 μm，由此可知，对于超高精度的微细加工来说，进行力诱导误差补偿十分必要。

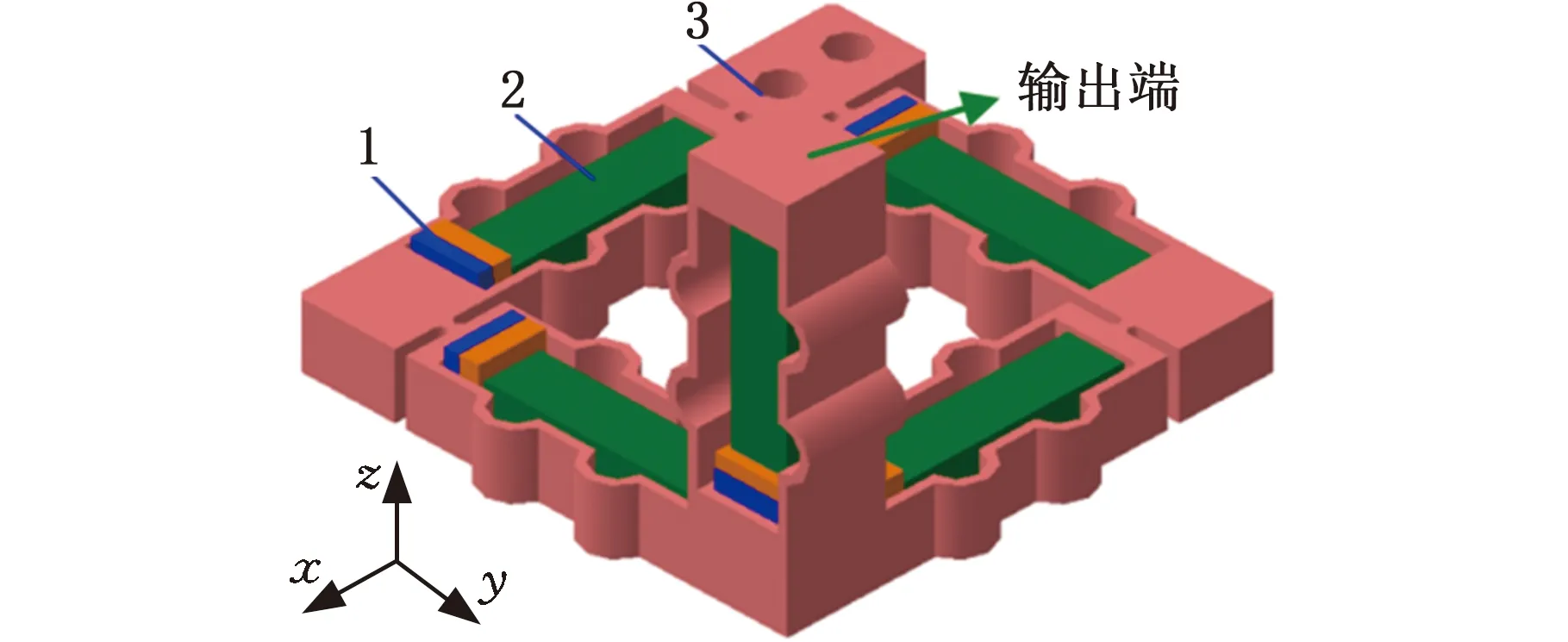
1.楔块 2.压电致动器 3.柔性铰链机构

机床零部件的刚度分析是进行力诱导误差补偿的重要步骤。为研究机床刚度链分布特性， SALGADO等[80]在传统三轴机床上评估了从机床床身到刀具之间所有零部件的刚度(图15a)。研究表明，在以往的刀具刚度分析中，圆柱形悬臂梁是最常用的简化模型[81]，然而，受刀具材料、尺寸以及模拟切削力等因素的影响，使用悬臂梁模型并不能对刀具的实际刚度进行准确的预测。此外，在切削力的作用下，机床、主轴、主轴安装支架、刀具等各部件的刚度对加工精度具有相同的影响。URIARTE等[82]基于Salgado的研究，对配备直径小于0.3 mm微细刀具的三轴微铣床进行了刚度链分析，并进行了力诱导误差评估(图15b)。在Salgado和Uriarte的研究中，由于机床尺寸和结构的不同，刚度链分布的结果完全不同。因此，进行超精密加工机床的刚度链分析，了解其各零部件的刚度分布和机床结构的薄弱环节，对提高加工精度、优化机床结构具有重要的意义，但目前该方面的研究成果较少。

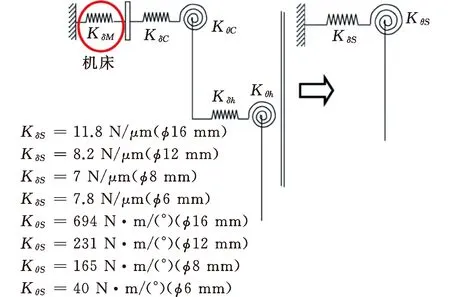
(a)传统机床刚度链评估[80]

在FIEs补偿方法方面，专家学者们也进行了相关的研究。SHI等[83]针对三轴机床FIEs设计了专门的加载装置进行等效切削力的加载，并使用激光干涉仪对加载过程中机床的挠度变形进行测量(图16)。然而，由于加载装置在Z轴方向上的限制，该研究仅对机床在X轴和Y轴方向上的FIEs进行了测量。DU等[84]提出了一种ANSYS参数化设计语言(fast ansys parametric design language, APDL)用于进行FIEs的快速计算，在不考虑机床变形的情况下，能够实现低刚度零件的力诱导误差补偿。MA等[85]针对曲面球头五轴铣削加工，提出了一种刀具FIEs镜像补偿方法，使加工精度成功提高了42%，但是，在前期的FIEs建模过程中，由于切削力系数的不确定性，使得切削力系数的测量较为困难。PAN等[86]提出了一种融合切削力模型预测和进给轴扰动观测的径向切削力估计方法，通过调整刀具轨迹来补偿刀具偏斜并防止钻孔直径偏差，精度较高。LI等[87]提出了一种基于静态子结构方法的力致变形预测模型和侧铣薄壁件及刀具变形的柔性误差补偿方法，解决了在薄壁零件的切削中切削力引起工件变形的问题。研究人员在三轴机床的刚度分析和力诱导误差补偿等方面已经做了大量的工作，但大部分研究都围绕刀具端的FIEs开展，对机床其他零部件的FIEs研究相对较少。此外，机床的结构对机床整体的刚度分布影响很大，五轴超精密加工机床由于旋转轴的存在，使得机床的刚度分布变得更为复杂，但目前为止，针对超精密加工机床中旋转轴-刀具系统的刚度链分析还鲜见报道。

(a)切削力加载原理图

4 超精密加工热诱导误差研究现状

机床温度变化导致工件与刀具相对位置发生改变所产生的加工误差称为热诱导误差[88-89]。在机床的连续运转过程当中，会持续不断产生热量，因此热诱导误差难以避免。而且，机床转速越高、加工负载越大，热误差影响就会越大。热误差产生的热源可分为外部热源和内部热源两大类[90]：外部热源包括光照、车间空调送风、工作人员体温等，主要以热对流方式影响机床精度，对于超精密加工来说，通过配备机床恒温控制系统，并对环境温度、湿度进行严格的控制，可以大幅降低外部热源对加工精度造成的影响；内部热源包括电机励磁热、轴承和丝杠螺母副摩擦热、切削热等，主要以热传导和热对流方式影响机床精度。对于超精密微细加工来说，切削产生的热量有限，温度变化对机床的加工精度影响大幅降低。但对于高速/超高速加工来说，高转速会使主轴电机、轴承和丝杠螺母副摩擦产生大量的热，对加工精度产生较大影响。为了降低内部热源对误差所造成的影响，研究人员针对机床结构做了大量的改进，例如，使用冷却液系统、热膨胀系数低的材料、对称结构等[91]。但受机床结构、成本等诸多因素的限制，这些方法只能在一定程度上降低热诱导误差。目前，热误差补偿技术仍然是最高效、便捷的方法。

4.1 主轴热诱导误差补偿研究现状

工件和刀具的相对位置是由进给轴和主轴的运动决定的，因此，机床的热诱导误差主要分为主轴热诱导误差和进给轴热诱导误差。主轴作为机床的核心部件，在高速运转时会产生大量的热[92]。主轴热诱导误差是超精密加工，尤其是高速/超高速加工热诱导误差的主要来源，为削弱发热对主轴的影响，目前主要有两种方法：

一是误差控制法，即控制进入主轴系统的热量或避免产生不均匀温度分布。例如，研究人员试图通过在主轴和轴承周围放置一层隔热材料来控制热流[93]，均衡温度分布，从而减少主轴系统中的热量，降低热膨胀[94]，通过建立温度控制系统来减少从外界环境传递到主轴系统的热量[95]。

二是误差补偿法，即通过调整刀具和工件的位置来校正误差。热诱导误差补偿技术出现在20世纪70年代后期，通过测量关键点的温度及热变形，建立温度和热变形间的数学表达式，利用滑台的运动进行热误差补偿，这项技术在20世纪80年代初被成功应用于坐标测量机上。之后，经过不断的发展和完善，形成了相对成熟的热诱导误差补偿方案：

(1)对主轴的温度分布和热误差进行理论分析、数值计算和实验研究。如YANG等[96]提出了一种最小二乘支持向量机(LS-SVM)的电主轴热误差模型，该方法在实施过程中考虑了刀具长度和热倾角，采用电涡流传感器和五点法测量径向热倾角和轴线的热变形，试验证实该方法可以预测 90%的热误差。JIN等[97]提出了多级LS-SVM热误差模型，用于进给系统热误差模型预测，在自制的进给系统试验平台上进行验证，结果显示，所提方法比普通的 BP 神经网络和 RBF 神经网络具有更好的精度。

(2)根据分析或试验结果建立热误差模型，描述温度与热误差之间的关系。如 YANG等[98]利用主球和电容传感器组成的实验装置测量主轴热误差，当主轴开始旋转时，热源(前轴承和传动箱)引起的温升导致主轴变形，主球和电容传感器之间相对位移的变化代表主轴的热误差，预测精度较高。

(3)根据模型预测热误差，并根据预测数据，通过在各轴中加入补偿值或调整坐标原点，完成热误差补偿。如西门子840D系统中[99]，热误差补偿模块作为附加单元，主轴的测量温度首先用于计算补偿值，通过可编程控制器将该值发送给系统，利用反馈截取的方法完成热误差补偿，FANUC系统中实施的热误差补偿正是基于原点移位法，在主轴热误差补偿研究中，许多学者采用外部补偿算子来实现补偿。

为进行准确的热误差分析，首先需要使用温度传感器、红外摄像机等设备对主轴系统的温度场进行精准的测试，获得主轴的热特性。其中，温度传感器的数量和测点布局十分关键，决定了热误差模型的准确性和鲁棒性以及误差补偿的有效性，研究人员提出了分组搜索、高斯积分、灰色系统等热关键点选择方法。主轴的热误差可以利用位移传感器，如电容传感器、间隙传感器等进行测量。将温度和热误差分别作为输入和输出，建立热误差模型，在对热误差模型进行验证后，利用模型预测的热误差，通过反馈截取法或原点移位法完成热误差补偿。WU等[100]通过深度学习卷积神经网络 (convolutional neural networks,CNN) 对水平和垂直主轴的轴向和径向热误差进行建模，该模型将热图像与热电偶数据结合在一起，建立了基于CNN的多分类模型，并验证了其准确性和鲁棒性， 模型预测准确性高达93%。WEI等[101]提出了一种次区域(sub-region,SR)方法来补偿工作台的热误差，将工作台划分为不同的区域，并为每个区域建立热误差补偿模型，然后组合起来补偿热误差，解决了整个工作台的热误差明显不同的问题。除了使用建立在数控系统外部的补偿系统以外，主轴热误差补偿也可以通过将热误差模型导出的热误差表集成到数控系统中来实现。热诱导误差补偿技术无需昂贵的硬件，如先进的材料和热管，并且可以在机床设计或制造的任何阶段实现，所需成本低，应用灵活[102]。

4.2 进给轴热诱导误差补偿研究现状

机床上的进给轴包括两类：直线轴和旋转轴。直线轴一般由丝杠螺母副或直线电机传动，热诱导误差对其精度影响较大，尤其是丝杠螺母副传动的直线轴。旋转轴一般由力矩电机或蜗轮蜗杆传动，热诱导误差影响的程度与其结构有关。目前，旋转轴热诱导误差的研究相对较少，在测试、机理分析、建模与补偿方面均存在一定困难，需要对其进行深入探索与研究[103-104]。

5 超精密加工误差补偿技术发展趋势

(1)高精度、高效率。超精密加工误差补偿研究大部分是针对某类误差进行单独补偿，其综合误差补偿精度会受到限制，但同时对多种误差元素进行补偿，会大大增加误差补偿的复杂性，降低误差补偿效率。因此，需要运用新型智能算法进行综合误差模型优化，使用高精度、高性能传感器进行误差识别，不断提高误差补偿精度和效率。

(2)模块化、通用化。多种误差源之间的相互耦合导致综合误差补偿难度较高，大部分误差补偿技术研究仍停留在实验室阶段。因此，构建清晰的综合误差补偿网络架构，按照误差源对综合误差进行模块化分类、补偿，针对不同结构、不同种类的机床，开发通用的误差补偿模型，形成成熟、实用、全面的误差补偿商业化软件系统是未来发展的趋势。

(3) 动态监测，持续优化。随着机床的长时间运行，误差模型的预测效果会受机床零部件磨损、应力变形等影响而逐渐变差，这就需要误差模型能够监测关键运动部件的磨损情况并进行特定调整，使误差模型的补偿精度得到长时间保持。在机床服役过程中，基于对机床加工过程大数据的采集与分析，对误差预测模型进行持续改进优化，使其预测精度愈加准确。

(4)智能化。集合数控技术、神经网络、实时监控、在线检测及CAD/CAM 等先进技术，以智能化、柔性化控制方式进行误差补偿，快速解决机床自身精度不足导致的加工精度不足等问题。

6 结论

(1)超精密加工误差补偿技术已受到国内外研究人员的普遍关注，但是目前在综合误差建模、预测和补偿等方面的研究整体上还处于探索阶段, 尚未形成完整成熟的技术体系和生产制造应用的技术能力。

(2)在几何误差补偿方面虽然已进行了大量的研究，但是传统几何误差补偿思路建立的误差模型或过于繁琐导致计算要求、测量成本过高，或通过简化所得误差模型过于简单导致误差补偿效果不佳。而且要实现位置无关几何误差PIGEs和位置相关几何误差PDGEs的完全分离，获得PDGEs的连续精确值，需要强大的计算能力以及大量的测量数据。因此，传统误差补偿的思路难以准确有效地解决PIGEs和PDGEs的耦合问题。此外，除了实验验证，目前并没有统一的标准来判断PIGEs和PDGEs误差分离结果是否准确，这将导致误差分离存在很大的偶然性。

(3)由于超精密微细加工中常采用气体静压轴承支承，气动涡轮驱动，其整体刚度较小，对切削力的敏感度更高，且该类主轴系统使机床的刚度分布变得更为复杂，故力诱导误差对超精密微细加工机床的影响显著增强且更为复杂。为进一步提高超精密微小自由曲面加工精度，有必要对超精密加工的力诱导误差补偿进行系统深入研究。

(4) 热诱导误差补偿在实验条件下一般可获得良好的补偿效果，但是当环境温度、主轴转速、进给速度、负载等条件改变时，特别是在运动信息复杂多变的实际切削过程中，模型的预测精度会有所降低。如何提高热误差模型对复杂运动状态的适应能力仍需进一步研究。此外，超精密加工机床旋转轴热诱导误差的研究相对较少，在测试、机理分析、建模与补偿方面均存在一定困难，需要对其进行深入探索与研究。