最优化方法可视化实验系统的设计与实现*
太原科技大学应用科学学院 姜旭磊 孙宝 范凯 王露梅 赵超
随着科技的日益发达和计算机技术的广泛应用,最优化方法愈发显示出其重要作用,最优化方法的重要性被愈来愈多的人所认识。实践表明,最优化方法已成为现代管理科学的重要理论基础和不可缺少的方法,被人们广泛地应用到公共管理、经济管理、工程建设、国防等各个领域,发挥着越来越重要的作用。而对于当今社会的大学生而言,则更应当具备这方面的知识和能力。事实上,在众多科技与工程领域中,如果没有最优化算法,就不可能产生一流的研究成果。正因如此,《最优化方法》课程成为大学理工科学生非常重要的一门必修课程,也是国际工程教育认证要求的必修课程之一。
《最优化方法》课程是以“微分方程”“线性代数”和“高等数学”等学科为依托,以程序设计语言为技术手段,以计算机为工具,讨论决策问题的最优选择之特点,构建求得最优化解的方法,运用数学方法研究各种系统的优化途径及方案,为决策者提供科学决策的依据[1]。该课程中同一问题的计算方法繁多,不同的方法又多是采取不同的思路得到的,这些基本特点使得《最优化方法》课程中存在的计算公式多而复杂,很难熟记[2]。而GUI 可视化实验系统在教学中的广泛应用,该系统同时具备用户界面友好性和可以简单操作实现各种图像分析等特点,使抽象的问题更加形象化,从而增加了学生的学习趣味、改善了教师的教学环境,使《最优化方法》的学习过程变得更加方便化、趣味化。此外,该系统也可为科研人员对最优化方法的研究提供便利。
1 MATLAB GUI 简介
MATLAB GUI 即为图形用户界面,是进行人机互动的重要手段,拥有巨大的功能,可实现多种复杂的程序模块。用户图形界面是MATLAB 的一个子模块,是由窗口、光标、按键、菜单、文件说明等对象构成的一个用户界面,是MATLAB 应用于可视化交互式中的重要工具[3]。
采用GUI 开发操作界面,使用者可不必编制繁琐的代码程序即可完成工作,系统自动编写好代码并生成fig文件和相应的m 文件。随着版本的升高,新的内容还将继续增加,同时具有强大的绘图功能,使得由MATLAB开发的程序可以被越来越多的用户所接受。
开启GUI 机制的密码为GUIDE、Appdesigner。本文选择了Appdesigner。相较于GUIDE,Appdesigner代码整洁,且采用典型的面向对象的编程方式,上手更快。另外,其可以按照App、Web 的形式发布,直接安装到MATLAB中,方便使用。最重要的是,为了更好地呈现可视化效果,Appdesigner 控件的UI 做的更加美观,控件的数目更多,界面更加直观。
2 系统的设计及实现
系统的研究内容主要包含《最优化方法》实验系统和可视化界面的实现两部分。技术路线如图1 所示。
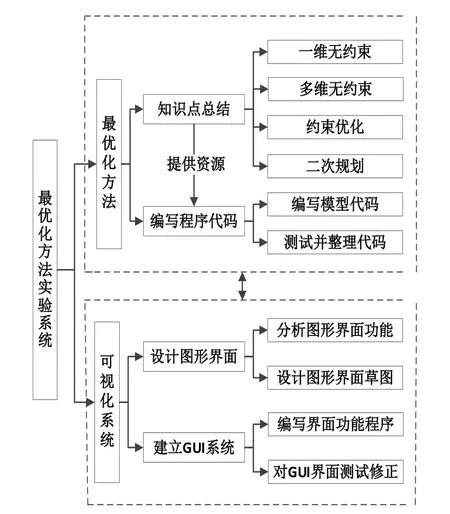
图1 技术路线图Fig.1 Technology roadmap
2.1 《最优化方法》实现
最优化方法可视化实验系统针对最优化方法的内容分成一维无约束、多维无约束、约束优化、二次规划4个模块,对各个模块完成最优化方法特定内容的实验,设置实验内容时全面考虑最优化方法内容的连贯性。
最优化方法可视化平台以学生为主体,通过搭建好的GUI 可视化实验系统,学生可通过界面上的菜单根据自己的需求选择合适的属性按钮,去完成计划的实验任务,同样,各个学生也可以根据不同的专业和需求,自行设计试验方案、适当调整实验中各变量的参数以得到多组实验结果并进行对比筛选[4]。在学生动手使用的过程中,可以把最优化方法的理论知识内化为认知结果,从而充分体现出最优化方法可视化实验系统的可操作性、连续性、实用性、交互性和可扩展性[5]。而基于最优化技术实践的灵活性和目的性,学生能够根据实验的要求调整操作按键和菜单,扩展实验内容,设计满足各个专业学生需求的应用方面的实验系统与界面,以此训练学生的发散性思维,调动其创新的积极性。
2.2 可视化界面系统
实验系统实现是基于MATLAB,但它完全不同于MATLAB 所要求编写程序,在命令窗口输入命令才能完成运算。系统采用的是最简单、用户最熟知的界面窗口操作,系统也是专门根据最优化方法及实验大纲设定,用户只需要通过界面上的菜单功能、控件功能和辅助信息等来完成操作系统。该系统具有高度的可视性,所以每完成一次操作,系统都可以同步显示操作信息,对于完成操作的用户,系统还可以将运行结果放在文本框中给出答案,还能够通过图形图像方式直观地表现出来。这样就极大地提升了答疑解惑的效率,减轻了用户的工作量。
2.3 可视化实验系统实例
为了介绍关于使用MATLAB GUI 构建最优化方法可视化实验系统的研究内容,以下使用了两个例子来描述实验系统中具体案例的设计过程,并从中感受GUI 图形界面的视觉效果和实验中所取得的收获。
2.3.1 牛顿法求解一维无约束问题的可视化界面实现
牛顿法是一种线性化的方法,牛顿法的核心思想是极值点处的一阶导数为0。牛顿法流程图如图2 所示。
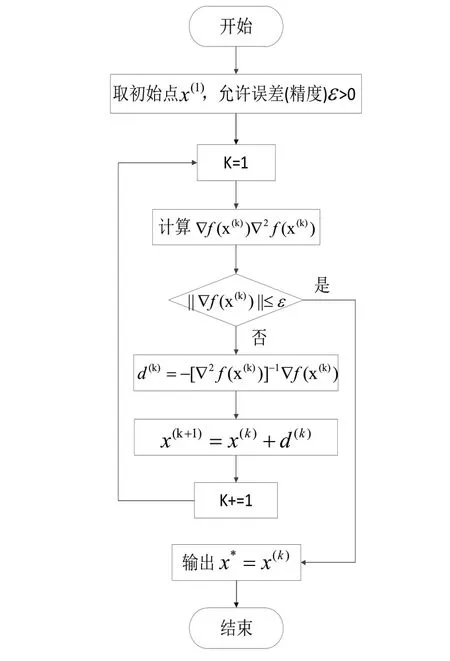
图2 牛顿法流程图Fig.2 Newton's method flow chart
该界面的实现需要进行以下几个主要步骤:
(1)我们需要一个已知的目标函数,及初始点与其所需精度;
(2)牛顿法的实现需要输入数据是目标函数、初始点以及所需精度,对应的输出数据为目标函数最值点,并构造对应的函数图像;
(3)之后根据上述分析的内容去绘制图形界面草图;
(4)对所需要实现的特定功能设置相应回调函数并编写相应的程序代码;
(5)在最后阶段对已实现的图形界面做出相应的测试和调整。
在界面中可以更换不同的目标函数、初始点以及精度。
2.3.2 模式搜索法
模式搜索法的基本思路,是沿着相邻的基点连线的方向进行搜索迭代。它主要分为两大步骤:(1)轴向搜索;(2)模式搜索。算法流程图如图3 所示。
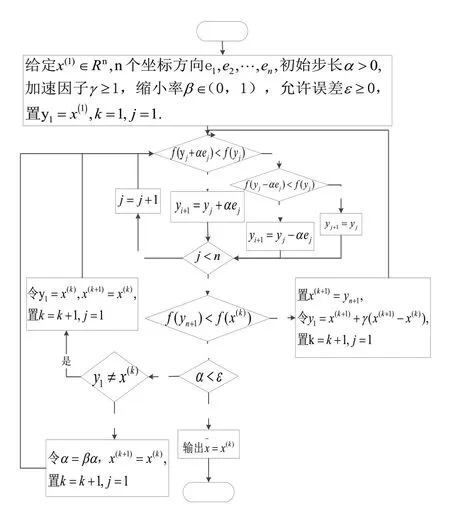
图3 模式搜索法流程图Fig.3 Flowchart of pattern search method
该界面的实现需要进行以下几个主要步骤:
(1)我们需要一个已知的目标函数、起始搜索点、初始步长、加速系数、收缩系数以及所要精度;
(2)模式搜索法的实现需要输出数据为目标函数最值点,并构造对应的函数图像;
(3)之后根据上述分析的内容去绘制图形界面草图;
(4)对所需要实现的特定功能设置相应回调函数并编写相应的程序代码;
(5)在最后阶段对已实现的图形界面做出相应的测试和调整。
3 结语
本文以牛顿法、模式搜索法的可视化实践为例,展示了采用MATLAB GUI 的最优化实验系统的操作过程。
可视化实验系统是以MATLAB GUI 作为载体,将最优化算法理论和MATLAB GUI 可视化技术相融合,让使用者在学习最优化方法理论的过程中,不需深入钻研完整代码就能够进行理论的计算过程。最优化方法与交互式实验系统,为最优化方法的理论教学与实验教学的有机融合提供了抓手,提高了学生学习兴趣。同时系统还具有以下4 项优点:
(1)可操作性。在教学中,学生作为主体,只以学习理论知识为中心,往往在实际操作中不理想,唯有亲身实践,才能将数学理论知识在实验实际操作过程中内化为学生自己的认知结果。该实验系统可通过MATLAB 程序设计实现所有模块和菜单功能。学生可以按照该系统一定的规范和要领操作完成实验,并得到准确的实验结果,不再需要MATLAB 编程就可以操作实验。并且在亲自操作完成实验的同时,使实验经验负载着数学知识成为认知内化的结果。
(2)交互性。最优化方法交互式实验系统通过GUI设计可视化用户界面,学习者利用界面上特有的操作按键和菜单完成设定的实验目标,从而得到实验结果;另外,也可以举一反三,自行设计实验方案、调整实验参数、以及在各个实验模块间查看、比较和应用。
(3)连续性和独立性。系统前期工作是进行高等数学的试验体系的建立和实现。它根据最优化方法的内容分为4 个独立的子系统,各系统实现最优化方法特定内容的实验。另外,系统也还注意到最优化方法内容的连贯性。各个子系统实现最优化理论方法特定的实验内容。同时,系统也全面考虑到每个章节部分内容的关联性。当处理复杂或符合多种类型的问题时,各子系统既独立体现不同内容,也连贯反映整体内容。从而使学生在实验中深刻体会各个方法的内涵和联系。
(4)可扩展性。本系统根据最优化方法的实验内容,设计了4 个子系统,分别承担了不同的实验内容。然而出于数学实验的高度灵活和目的性,学生能够针对实验的目标以及自身实验的要求添加和修改操作按键和菜单、从而扩展实验内容,设计出满足各个专业学生不同实验和操作所需求的实验系统和界面,以此训练学生的创造思路,调动其创新的积极性。
引用
[1] 刘燕,宋清华,王威强,等.培养“过控”专业大学生的工程技术素养的探讨[J].化工高等教育,2014,31(3):28-29+50.
[2] 裴明佳,孙宝.基于MATLAB GUI的数值分析教学实验系统开发[J].信息系统工程,2021(8):174-176.
[3] 张光辉,任敏.基于MATLAB GUI的数值分析实验系统设计[J].河北北方学院学报(自然科学版),2017,33(9):50-53.
[4] 臧营邦,刘旭阳,王加敏.基于MATLAB App Designer的最优化方法辅助教学设计[J].电脑与信息技术,2022,30(1):81-83.
[5] 唐世星,刘颖华.基于GUI的高等数学实验教学系统[J].承德石油高等专科学校学报,2012,14(3):83-86.

