面向设施配置空间优化的量子进化算法
周鑫鑫,袁林旺,吴长彬,韩佩佩,黄 敬,俞肇元
1. 南京邮电大学地理与生物信息学院,江苏 南京 210023; 2. 南京邮电大学江苏省智慧健康大数据分析与位置服务工程实验室,江苏 南京 210023; 3. 南京师范大学地理科学学院,江苏 南京 210023
空间优化是实现空间要素资源合理利用的重要途径,是地理信息科学的重要研究方向之一,旨在实现空间约束条件下地理决策问题的最优解计算[1],已广泛应用于土地利用配置[2]、地理模拟优化[3]、交通布局配置[4]、设施配置空间优化[5]等领域。设施配置空间优化是空间优化问题的典型范例,以计算研究区内多个设施的地理位置、容量为结果,以提升地理空间布局结构合理性为目标。根据设施分布连续程度分类,设施配置空间优化分为离散设施空间优化、连续设施空间优化;根据关键构成分类,可分为3个部分:目标函数、约束条件及优化方法[6];根据目标函数和约束条件差异性,又可形成多种设施配置模型,如:P中值模型、P中心模型、覆盖模型、动态选址模型、多目标模型、网络中心模型等[7],各模型本质仍为设施资源、需求者、服务质量三者的博弈平衡。

2020年美国国家地理空间情报局指出需发展地理空间优化量子计算方法,以求解复杂的、多变量的地理空间优化问题。类比于模拟退火算法翻越过“山峰”过程易陷入局部而无法逃逸“山谷”,日本学者西森秀稔吸纳量子力学中的量子隧穿效应理论,提出“山峰”可以“穿过”的量子退火算法,为量子退火计算机提供理论基础[17]。本文借鉴量子计算思想渊源[18],提出应用量子进化机制构建设施配置启发式算法科学假设,以适用于城市耦合环境下地理现象相关性和异质性约束,实现设施配置搜索解质量提升。量子进化机制是实现高性能、高质量计算的重要方向,已于硬件和算法层面论证,如量子遗传算法[19]、量子进化算法[20-21]、量子密码算法[22]、量子搜索算法[23]。近年来,结合量子进化机制的新型智能算法包括:量子人工神经网络、量子的模式识别算法、量子衍生进化算法、量子的聚类算法、量子退火算法、量子小波与小波包算法[24]等。综上所述,针对如何设计出符合离散型设施配置空间优化的量子进化算法,本文首先于第1节阐述设施配置空间优化基本流程,然后在第2节和第3节对量子计算特性和量子进化算法设计流程进行剖析,最后于第4节和第5节进行试验验证和总结。
1 设施配置空间优化流程
从概念设计视角,设施配置空间优化过程可看作3种空间域的转换,即:地理空间域、决策空间域和目标空间域(图1),适用于各种设施,包括:教育、文体、卫生、商业、饮食、服务和行政经济管理等。地理空间域是指居民日常生活的物理空间,涉及居民区、已建离散设施及已建交通路网条件等。决策空间域是指通过对地理空间问题定义和测度而得到的求解空间,其中居民区抽象为需求点,已建离散设施抽象为已建供给点,并根据实际城市规划条件、宜建、禁建条件而形成的待建候选点集合。目标空间域包括设施空间布局配置(layout allocation)及空间重定位(relocation),前者以规划新建设施位置和规模为目标,后者以对已建服务设施进行资源重新调度为目标。参照文献[25]中的管理决策分析对决策分析框架的定义,决策分析包括:识别问题、设计目标、拟订方案、评价分析、优化方案、实施反馈。本文总结并形成设施配置空间优化框架流程的7个环节(图1):①问题定义与测度;②现状评价;③目标函数;④空间配置类型;⑤约束条件;⑥优化算法;⑦分析对比。从地理空间域到决策空间域是一个测度和范化的过程,依赖于环节①和环节②;从决策空间域到目标空间域是一个优化求解的过程,依赖于环节③—环节⑦。因环节不同,设施配置空间优化框架可组合成多种研究问题,本文聚焦研究有容量约束的离散型设施组合配置问题。

图1 种空间转换关系及设施配置流程Fig.1 Schematic diagram of three domains transformational relation and the flowchart of facility allocation
2 量子计算特性与算法结构
量子计算具有并行性、状态叠加性等特性,在组合优化问题中具有显著优势,因此,在设施配置空间优化问题中引入量子计算机制,是突破高维多峰空间优化问题的全新途径。基于量子计算原理而模拟设计出的优化算法结构称为量子进化算法,包括基于量子物理学的搜索算法和基于量子计算与传统智能优化算法结合形成的量子衍生智能算法。量子衍生智能算法实现了量子原理与智能计算的结合,利用量子并行计算等特性弥补了传统智能算法的某些不足,如:传统智能算法搜索速度慢、易出现早熟现象,主要算法涉及量子退火算法、量子进化算法、量子神经网络、量子贝叶斯网络、量子小波变换、量子聚类算法等[17]。这些算法的共同点是应用了量子计算机制或启发机制,符合量子力学行为特征,延续了量子计算优势。受限于量子计算机硬件发展,这些算法目前主要通过模拟量子计算实现,但它们较传统智能算法仍具有显著优势。
2.1 量子计算特性
量子计算特性概括为状态叠加性、状态相干性、量子并行性、状态纠缠性[18]。这些特性的形成来源于量子比特、量子概率幅观测及量子门更新。与经典比特不同,量子比特(Qubit)可记录量子位的概率幅,可同时存储和表达“0”和“1”两种状态,可表示为|ψ〉=α|0〉+β|1〉,α、β是两个复常数,称为量子比特概率幅,满足|α|2+|β|2=1,|0〉和|1〉分别表示“0”和“1”两种状态,形成状态叠加性。状态相干性体现在基态|0〉的概率幅,由于量子门作用得到增加,同时|1〉的概率幅度降低,对在基态的线性叠加状态下的量子系统|φi〉是相干的,当周围的环境作用于该系统时,所处的叠加状态不再存在,并按照|pi|2坍塌到某一个唯一的基态|φi〉。量子并行性体现在一旦量子门对空间中的量子状态进行操作,其中所有的基态都会受到影响。状态纠缠性体现在当两个子系统中存在的一些状态并相互作用时,状态会同时被修改。
2.2 经典量子进化算法结构
文献[26—27]总结了经典量子进化算法流程,算法流程见算子1。该算法流程含7个步骤,主要涉及量子比特编码算子、适应度评价、概率坍塌算子、量子门更新算子、精英策略等。
算子1:传统量子进化算法流程
输入:设定迭代开始条件
输出:最后代数种群的个体
量子种群初始化Q(t),令迭代次数t←0,根据量子比特编码算子初始化量子种群Q(t);
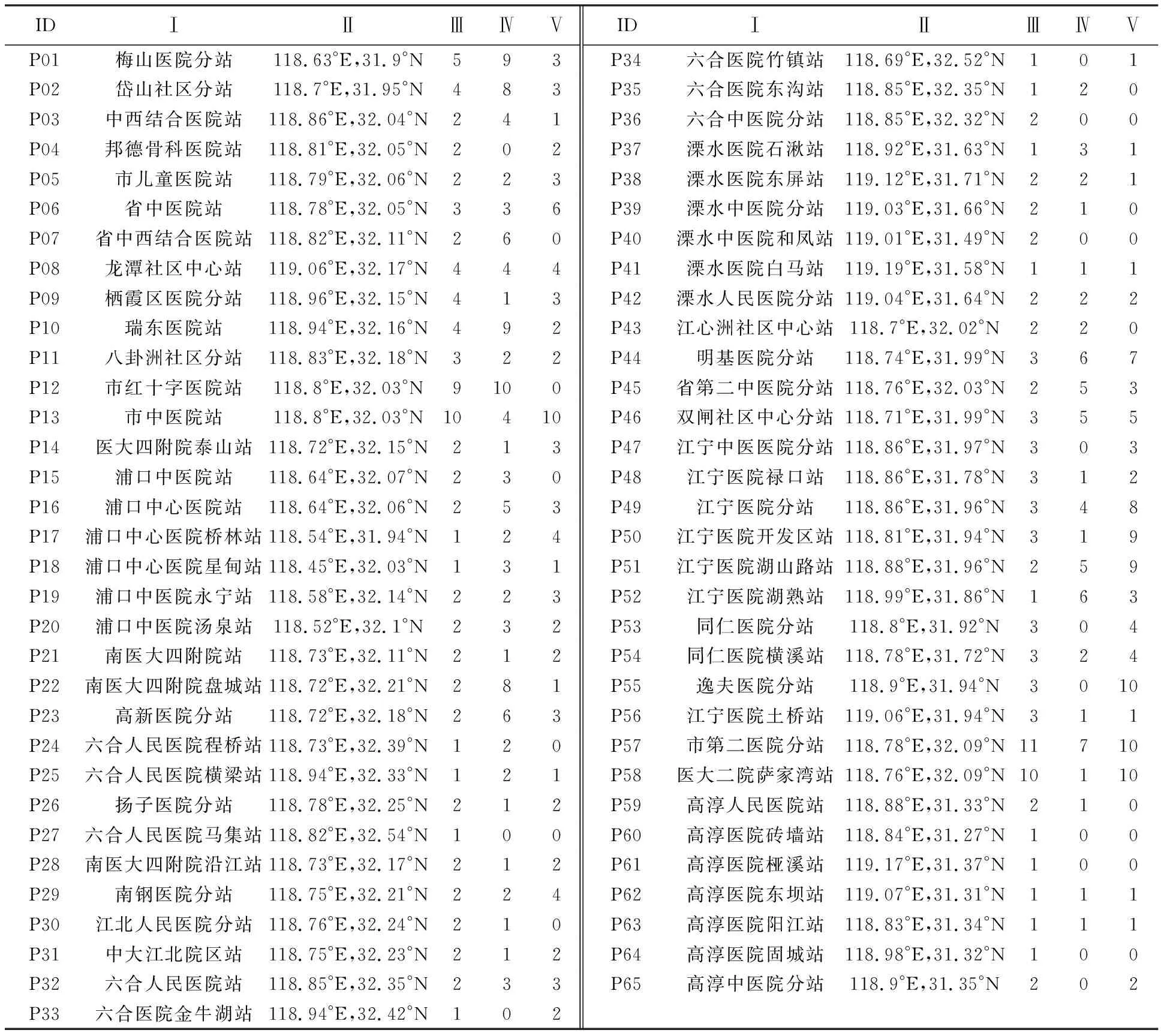
whilet 量子染色体坍塌观测,通过概率坍塌算子,确定每个量子染色体的解,得到解种群P(t); 对解种群P(t)进行适应度评价,根据目标函数,来评价P(t)中每个解个体的适应度。其中,目标函数应实际应用问题而定义; 精英策略选择,从P(t)中选择最好的解,并保持到精英种群B(t)中; 利用量子门U(Δθ)算子更新形成新一代量子种群Q(t+1),使用量子门U(Δθ)更新机制计算得到新一代量子种群Q(t+1),详见量子门U(Δθ)算子; 对新一代量子种群Q(t+1)补充精英个体,从B(t-1)选择出最好量子染色体,并存储至新一代量子种群Q(t+1); t←t+1; end 经典量子进化算法在理论连续函数上已被证明可用、高质量,但集成至设施配置空间优化问题中,面临着结合难的挑战。究其原因,经典量子进化算法使用二进制量子染色体编码,是将量子状态又重新随机地转换为经典比特状态。这种观测、编码方式在实际应用问题求解中具有一定局限性,尤其是总量约束的整数组合优化问题[25],如在|0〉和|1〉的叠加态的染色体中会导致染色体不稳定,存在“长度灾”,且不适应于条件约束问题,如总规模约束、整数约束等。已有研究针对经典量子进化算法的“长度灾”提出基于实数编码的量子进化算法[26-30],此类算法在迭代过程中,首先改进编码和解码过程,从而提高了求解效率;然后改善|0〉和|1〉的叠加态编码带来的精度丢失不足;最后,改善因求解问题维度变大引起的“长度灾”。 本文以有容量约束的离散型服务设施选址为设施配置基础模型,目标函数R(t)可为最小化/最大化代价函数(例如:最小化通行时间、最大化公平性),讨论并设计基于实数编码的量子进化算法,提出面向设施配置空间优化的量子进化算法(quantum evolutionary algorithm for spatial optimization of facility allocation,QEA-SOFA),流程如图2所示,主框架与经典量子进化算法[24-25]保持一致,包含“种群生成-种群进化-种群评价”,在编码结构、量子变异、离散交叉等算子上改进。 图2 QEA-SOFA算法流程Fig.2 Flowchart of QEA-SOFA algorithm (1) (2) 式中,关于三角变换初始角度的确立,采用如下方式 (3) 式中,rand()函数为(0,1)之间的随机数;i表示种族规模,i=1,2,…,m;j表示量子位,j=1,2,…,n。 算子2: 四倍体量子整数编码染色体总量约束算子 输入:上限UP,下限BOTTOM,染色体维度M,总量约束值E_setting,四倍体量子染色体 精细调平: WhileΔ!=0 do IfΔ>0 then Δ+=1 end else ifΔ<0 then Δ+=1 end elseΔ==0 Break end end end (4) (5) 算子3: 越界控制算子片段 end end (6) (7) (8) 2种方式的计算结构、变量内涵保持一致,不同之处在于进化尺度部分的确立方式。 从理论和应用两个层面,证明QEA-SOFA算法的有效性、用益性,包括试验1(理论函数试验)、试验2(应用试验)。其中,试验1以Ackley和Griewank标准测试函数求解为研究情景,试验2以南京市急救服务设施配置空间重定位优化为应用情景。 (1) 函数与参数设置。为考察QEA-SOFA算法在理论高维多峰函数(high-dimensional multimodal function)上求解有效性,本文选取实数编码遗传算法(real-coding genetic algorithm,RCGA)[29]为对照组,并以Ackley和Griewank函数为标准测试函数,优化目标为求解全局最小值。图3为Ackley和Griewank函数2维曲面图,可知Ackley和Griewank函数具有典型“多峰”结构特征。Ackley和Griewank函数维度设定为100维,且存在上下边界,2个测试函数的理论最优值均为0(表1)。QEA-SOFA算法与RCGA算法参数设置一致,变异概率设置为0.05,交叉概率为0.66,种群规模为200个,进化代数为2000代,染色体长度为100;QEA-SOFA算法的特有参数设置,变化幅度初始值θ0=0.4×π,学习率设置为0.05。试验分2组对比场景,场景1是无约束条件场景,场景2是有约束条件场景(具体约束条件为总量约束和整数编码约束,Ackley函数的总量约束参数E_setting设置为500,上边界UP设置为10,下边界BOTTOM设置为1;Griewank函数的总量约束参数设置为1000,上边界UP设置为50,下边界BOTTOM设置为1)。 图3 高维多峰测试函数2维可视化Fig.3 2D visualization of high-dimensional multi-peak test function 表1 测试函数数学定义Tab.1 Mathematical definition of test functions (2) 算法对比结果。采用Ackley和Griewank函数的各代目标均值(average value)和最优值(best value)作为评价QEA-SOFA算法和RCGA算法搜索解的质量指标,场景1和场景2的迭代收敛过程如图4所示。场景1中(图4(a)、(c)),QEA-SOFA算法在Ackley、Griewank函数上的搜索解适应度明显优于RCGA算法的搜索解适应度,且其代际间收敛速度更快,于250代左右已接近最优值,而RCGA算法于2000代时的最优值仍劣于QEA-SOFA算法结果。场景2中(图4(b)、(d)),当对RCGA算法增加总量约束和整数编码后,其求解过程中各代均值呈现显著波动变化,收敛缓慢;而QEA-SOFA算法求解过程呈现“快速下降,然后低频波动”变化。这也说明QEA-SOFA算法在增加约束条件后仍保持相对更稳定的搜索特性,该特性取决于量子变异机制的多态表达。综述,QEA-SOFA算法较RCGA算法而言,具有显著解质量增强效用。 图4 收敛过程对比Fig.4 Convergence process comparison 为验证QEA-SOFA算法在设施配置空间优化问题的价值,试验2以南京市为研究区,以急救站设施空间重定位[35]为研究问题。南京市位于长江下游中部地区,是国家区域中心城市、特大城市,常住人口850万人,综合医疗资源丰富,公立医院241所、急救站65个。目前,南京院前急救反应时间远大于国家标准,南京市急救平均反应时间为16 min (http:∥jiangsu.sina.com.cn/news/s/2018-01-31/detail-ifyqyuhy8000404.shtml),尚未达到国家标准要求,且急救反应时间20 min以上的占比过高。研究区内各急救站的救护车资源配置与区域人口分布、交通条件仍存在不协同的矛盾,呈现出“富集、贫瘠”公平性差异大的情景。因此,综合人口、交通和医疗服务的典型性,本文以特大城市南京作为研究区。人口分布数据为基于手机信令的人口空间分布值,交通数据为高德地图API实时导航路径数据,研究单元为街区单元数据。研究问题凝练为“如何在已有65个急救站上,通过对169辆救护车空间重定位配置,优化公平性目标,实现公平性目标函数的最大化”,目标函数为急救服务设施可达性的公平性函数。公平性函数是以可达性模型作为基础,以各居民点到设施的公平性差异性的倒数最大化为目标的设施配置空间优化模型[36],实现了设施配置不一致性的评价,目标函数的详细定义参考文献[36]。此外,结合优化算法参数默认设置和研究区实际急救站资源配置上下限(BOTTOM、UP),确立面向急救设施配置应用试验的参数设置,见表2。 表2 QEA-SOFA算法参数设置说明Tab.2 Parameter setting description table of QEA-SOFA algorithm 开展急救服务设施配置试验,求解公平性最大化适应度值,得迭代收敛图(图5)。QEA-SOFA算法与RCGA算法均呈现收敛增大趋势,两者平均适应度呈现“先上升后震荡”,最大适应度呈现“先上升后稳定”收敛趋势,说明两者对空间优化均奏效。但QEA-SOFA算法在适应度质量和代际进化速度上明显优于RCGA算法,QEA-SOFA算法的平均适应度在迭代次数为5时趋于震荡,而RCGA算法的平均适应度在迭代次数为125时才停止增长,趋于平缓。QEA-SOFA算法在搜索解适应度上明显优于RCGA算法,QEA-SOFA算法的最大适应度值趋近100,而RCGA算法的最大适应度值趋于60,相对质量提升约66%。以上结果说明QEA-SOFA算法在急救服务设施配置求解中搜索能力更强,改善了高维多峰优化容易陷入局部搜索的不足。 图5 QEA-SOFA算法与RCGA算法试验结果对比Fig.5 Comparison diagram of experimental results between QEA-SOFA algorithm and RCGA algorithm 为表征两种算法对不同站点配置结果带来的差异性,本文构建急救设施配置结果对比表(表3)。由表3列Ⅲ可知,优化前急救资源集中分布在鼓楼区、秦淮区;由表3列Ⅳ和Ⅴ可知,优化后配置结果更倾向于将资源调度至建邺区、雨花台区及周边近郊区调度。推测成因,建邺区、雨花台区及周边近郊区居住人口密集,产业聚集,需求量较大,人均急救资源较低,所以呈现需求增长的趋势。优化结果与人口规模成正比关系,说明RCGA算法和QEA-SOFA算法可根据人口、交通可达性条件调度设施,以改善资源“富集、贫瘠”公平性差异。此外,选取位于典型区域的站点,如:浦口大学城区域(ID为:P14、P22、P23、P26、P28、P29、P30、P31)、江宁大学城区域(ID为:P47、P49、P50、P51、P53、P55),发现RCGA算法提高了浦口大学城区域的急救资源量,以P22、P23急救站最典型,而QEA-SOFA算法提高了江宁区大学城区域的急救资源量,以P49、P50、P51、P55急救站为典型。结合田野调查法,江宁大学城拥有17所高校,在校生约25万人,周边居民及园区人口密集;浦口大学城入驻高校7所,在校生约10万人,周边居民及园区人口相对稀疏。该人口分布差异间接说明江宁大学城及其周边范围对潜在急救资源需求量更大,应当提升江宁大学城区域的急救资源配置量。对比典型区域的规模、人口、资源配置量,发现QEA-SOFA算法结果更符合田野调查结果。从人口空间分布视角,该结果也论证了QEA-SOFA算法对典型空间异质区域的局部搜索具有更优精度,说明QEA-SOFA算法在局部高维多峰区域的搜索能力更强。 表3 急救设施配置结果对比Tab.3 EMS facility spatial allocation results comparison 本文提出面向设施配置空间优化量子进化算法,用于求解高维多峰空间优化问题,改善传统算法易陷入局部搜索的不足,搜索解质量得到提升,并将其应用于城市急救设施配置空间优化。本文算法可更好地适应城市耦合环境下地理现象相关性和异质性约束,编码表达状态更多,对空间异质区域局部搜索具有更大探测尺度,这表明量子进化机制在求解地理空间优化问题中具有巨大潜力。但是,当前研究仍存在不足:①城市专项服务设施规划导向、时空地理信息是城市公共基础设施管控、规划的研究基础[39],本文侧重于算法模型,而弱化了城市公共基础设施规划理论、时空信息获取与分析方法,未来研究中将加强论述;②QEA-SOFA算法未能完全从理论层面开展收敛性数理证明;③当前量子进化算法实现了与设施配置的融合应用,但量子并行高性能优势尚未发挥,仍处于地理优化问题量子方法研究的萌芽阶段。QEA-SOFA算法仍运行于经典计算机(冯诺依曼架构计算框架)上,无法完全克服模拟量子编码和量子变异算子的耗时缺陷,未来研究工作将重点围绕如何将地理优化量子算法运行于量子计算机[40],如:D-Wave(量子退火)、IonQ(离子阱)、Rigetti(超导),实现在性能和质量的双提升研究[17]。3 面向设施配置空间优化的量子进化算法

3.1 四倍体量子染色体编码算子


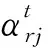
3.2 总量约束算子

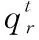
3.3 量子变异算子






3.4 量子交叉算子

4 试验与应用
4.1 试验1:QEA-SOFA算法在理论高维多峰函数上求解



4.2 试验2:QEA-SOFA算法在设施配置中的应用


4.3 算法时间复杂度分析
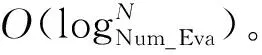
5 结 论

