熵正则化下的变分深度生成聚类模型

张志远，陈亚瑞，杨剑宁，丁文强，杨巨成

天津科技大学 人工智能学院，天津300457

无监督聚类是机器学习领域一个富有挑战性的研究方向，它是将无标签的数据通过某种度量聚集在一起的过程。传统聚类的方法一般分为两种：基于相似度的聚类和基于特征的聚类。基于相似度的聚类方法是通过某种距离度量来表示数据之间的相似性，并将相似度高的数据聚集在一起，经典代表算法是谱聚类（spectral clustering，SC）[1]。基于特征的聚类方法是在数据的特征空间中，依照某种度量来进行聚类的，经典代表算法包括K-均值方法（K-means）[2]和高斯混合模型（Gaussian mixture model，GMM）[3]。传统聚类算法实现简单高效，被广泛应用于各种实际问题。但是传统聚类算法的瓶颈在于它无法学习到数据的高层特征表示，同时也很难处理高维度的大规模数据集。

近几年，深度学习在人工智能领域掀起热潮，它利用深层神经网络强大的学习能力来挖掘数据的特征信息，可以高效处理高维度、大规模的数据集。深度学习的特性为聚类算法提供了新的思路，将深度学习与聚类算法结合起来，首先通过深层神经网络学习数据的特征信息，再结合聚类算法对特征信息进行聚类，最终实现端到端的深度聚类。已有的一些研究工作[4-5]将深度学习与基于特征的聚类方法结合起来，利用神经网络来学习数据在隐空间中的结构化信息，再在隐空间中使用传统聚类算法对隐向量进行聚类，最后联合深度模型和聚类算法的优化目标，利用随机梯度下降法来训练神经网络的参数。还有一些研究工作[6]将深度学习与基于相似度的聚类方法结合起来，主要用来解决传统聚类算法的瓶颈问题。

相比传统聚类模型，深度聚类模型不仅解决了传统聚类算法的瓶颈问题，而且大幅度提高了模型的聚类精度。具体地，Yang 等人[7]提出了深度聚类网络模型（deep clustering network，DCN），该模型在自编码器的优化目标中加入了聚类损失来学习数据的隐向量与聚类分配。Xie 等人[8]提出了深度嵌入聚类模型（deep embedded clustering，DEC），该模型首先使用自编码器和K-means 算法来初始化模型参数，然后将定义好的KL 散度作为优化目标，利用随机梯度下降算法进行参数更新。Zhang 等人[9]提出了混合自编码模型（mixture of autoencoder，MIXAE），该模型联合多个自编码器来学习数据在隐空间中的特征表示，其中，一个自编码器学习一种类别信息，并使用神经网络来计算隐向量的聚类分配。上述模型以不同的方式建模，可以达到较好的聚类性能，但是很难扩展到聚类之外的其他任务，如生成数据。

深度生成模型结合了深度神经网络和概率生成模型，是深度学习领域的重要研究方向之一，经典的深度生成模型包括：变分自编码（variational autoencoder，VAE）[10]模型、生成对抗网络（generative adversarial nets，GAN）[11]模型和对抗自编码（adversarial autoencoders，AAE）[12]模型等。已有研究工作表明用深度生成模型进行数据聚类，不仅可以实现高精度的聚类任务，而且可以生成高质量的数据[4-5，13-17]。具体地，Jiang 等人[4]提出了变分深度嵌入（variational deep embedding，VaDE）模型，该模型使用VAE 模型作为基础框架，并假设隐向量的先验概率分布为GMM，通过VAE 模型学习生成数据的能力，通过GMM 在数据的隐空间完成聚类分配的任务。Dilokthanakul等人[5]提出了高斯混合变分自编码（Gaussian mixture variational autoencoders，GMVAE）模型，该模型与VaDE 模型的本质思想相同，区别在于GMVAE 模型比VaDE 模型多了一个随机过程，用来配合神经网络计算GMM 的均值与方差。然而VaDE 与GMVAE 对隐向量分布的学习都是独立的，无法捕捉到数据的局部结构信息。Yang 等人[13]提出了基于图嵌入的深度高斯混合（deep Gaussian-mixture VAE with graph embedding，DGG）模型，该模型在VaDE 模型的基础上引入了图嵌入技术，将每一个样本数据看成图中的点，将JS 散度（Jensen Shannon divergence）作用在每一条边上，以此描述样本数据间的结构信息。实验表明，DGG 模型的聚类精度相比VaDE 模型有很大的提升。VaDE 模型、GMVAE 模型和DGG 模型在训练初期都存在局部收敛问题[14]，因而这些模型在训练初期都使用了自编码器来进行预训练，解决该问题的方法还有最小化信息约束算法[14]。

本文在VAE 模型框架下提出VDGC-ER（variational deep generative clustering model under entropy regularizations）模型。首先，VDGC-ER 模型的生成模型以连续隐向量作为模型的特征表示，并对连续隐向量进行GMM 先验建模，以离散隐向量作为类别向量。模型的变分推理模型是基于均值场的分解形式，可分解为编码和聚类两部分。与VaDE 模型不同的是，该模型通过对离散隐向量引入样本熵正则化项来增强预测聚类类别的区分度，即增大预测为真的分量与预测为假的分量之间的距离，提升模型的聚类精度；VDGC-ER 模型通过对离散隐向量定义聚合样本熵正则化项，降低聚类不平衡，避免局部最优，提升生成模型生成数据的多样性。进一步，采用蒙特卡洛采样及重参策略近似模型的优化目标，并利用随机梯度下降法求解模型参数。在训练时对重构误差项设置权重，缓解模型在训练初期的局部收敛问题。最后，为了验证模型的有效性，分别在MNIST 数据集、HHAR 数据集、REUTERS 数据集和REUTERS-10K 数据集上，设计了对比实验验证VDGC-ER 模型不仅可以生成高质量的样本，而且可以显著提升聚类精度。

1 变分自编码模型

VAE模型是由Kingma 和Rezende两个团队于2014 年分别独立提出的，该模型有效结合了变分贝叶斯方法和深层神经网络，是经典的深度生成模型之一。相比传统的自编码模型，VAE 对隐空间注入了噪音，使隐空间服从于某种分布，从而丰富了隐空间的表达能力，并使模型具有生成数据的能力。

VAE 假设高维数据x是由低维隐向量z生成，其生成模型表示形式为：

其中，p(z)=N(z;0,I)表示隐向量先验概率分布，I表示单位矩阵；p(x|z)=N(x;μ,σ2I) 表示条件概率分布。VAE 中数据的生成过程为：先从先验概率分布p(z)中采样隐向量z，然后从条件概率分布p(x|z)中采样生成数据x。

上述生成模型中的概率推理问题是求解数据集的边缘似然概率p(X)及隐向量的后验概率分布p(z|x)，考虑无法精确计算这两个概率分布，VAE 引入变分推理模型q(z|x)来近似后验分布p(z|x)，将推理问题转化为了优化问题。对于单样本点x，VAE 的证据似然下界（envidence lower bound，ELBO）为：

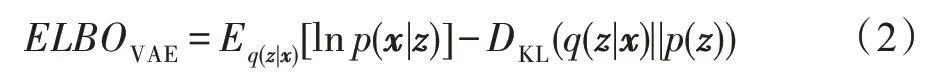
其中，式（2）右边第一项表示重构误差，第二项表示概率分布q(z|x) 与p(z) 之间的KL 散度，用来约束VAE 模型的隐空间。

VAE 模型优化目标为最大化式（2），可以通过蒙特卡洛采样近似优化目标，并利用随机梯度下降算法求解优化目标。

2 基于熵正则化的变分深度生成聚类模型

本章首先给出VDGC-ER 的生成模型和变分推理模型，然后引入样本熵正则化项与聚合样本熵正则化项，并给出模型的优化目标，最后利用蒙特卡洛采样及随机梯度下降进行优化问题求解。

2.1 生成过程

VDGC-ER 的生成模型以连续隐向量作为模型的特征表示，同时引入离散隐向量对连续隐向量进行GMM 先验建模，并以离散隐向量作为类别向量。令x∈RD表示观测向量，z∈RM表示低维连续隐向量，y表示为离散型指示向量，VDGC-ER 生成模型的联合概率分布表示为：

该模型的数据生成过程为：首先从概率分布p(y)中采样y，以此来决定从哪个组件采样z；然后从概率分布p(z|y)中采样隐向量样本z；最后通过概率分布pθ(x|z)采样数据x。

2.2 变分推理模型

对于VDGC-ER 的生成模型，通过引入变分分布qϕ(z,y|x)来近似求解p(z,y|x)，其中ϕ表示推理模型的神经网络参数。根据均值场变分推理思想，将qϕ(z,y|x)分解为编码和聚类两部分：

根据生成模型联合概率分布，如式（3）所示，和推理模型分布，如式（7）所示，可以得到VDGC-ER 模型的证据似然下界（ELBO）为：

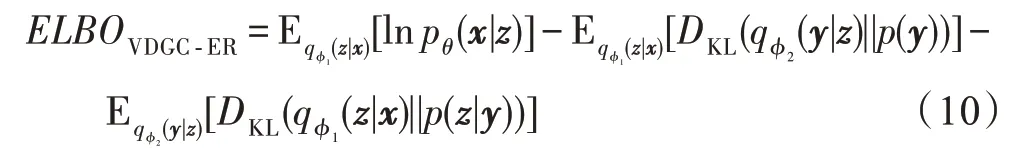
其中，等式右边第一项记为重构误差项；第二项是基于y的后验概率分布与先验概率分布p(y)之间的KL 散度，记为先验项；第三项是基于z的条件概率分布之间的KL散度，记为条件项。

图1 给出了VDGC-ER 的生成模型和推理模型。其中，白色圆表示隐变量，灰色圆表示观测变量，黑色实心圆表示模型的参数。图1（a）表示VDGC-ER的生成模型，图1（b）表示VDGC-ER 的推理模型，N表示样本数量。

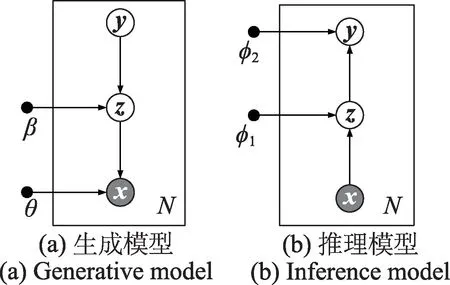
图1 VDGC-ER 的生成模型与推理模型Fig.1 Generative model and inference model of VDGC-ER

2.3 熵正则化项

离散型指示向量y在给定样本x条件下的近似后验概率分布为：

在优化过程中，上式中的期望可以通过基于重采样的蒙特卡洛方法计算。变分分布反映了某样本x聚类的概率输出。在聚类过程中，通过变分分布的最小化熵约束来提高聚类准确性，达到平衡硬分类与软分类的作用。对于变分分布，定义熵约束：

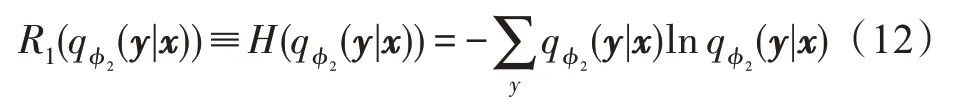
该约束又称为样本熵正则化项。式（12）的值越小，变分分布的熵越小，则样本x聚为某一类的概率越大，更接近于硬分割。

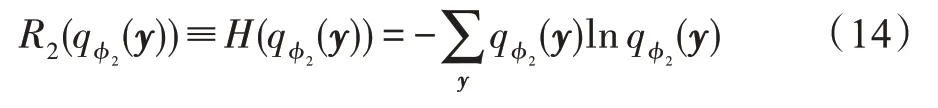
该约束又称为聚合样本熵正则化项。当式（14）的值越大，聚合后验概率分布的熵越大，则数据集X对应的隐向量集Y的分布与均匀分布的距离越小。

最终，结合式（10）、式（12）与式（14），在数据集X上，VDGC-ER 模型的优化目标为：

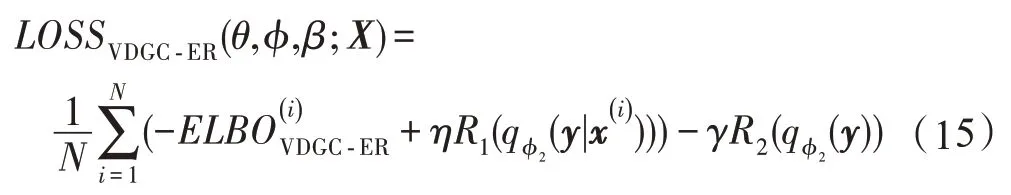
其中，η和γ表示正则化系数。此时求解的优化问题为：

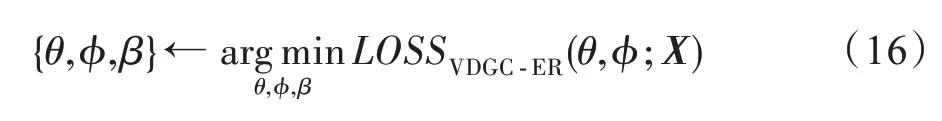
2.4 模型优化求解问题

为了求解优化问题式（16），首先对含有期望的ELBO 项使用蒙特卡洛采样及重参策略来估计，然后利用随机梯度下降方法进行参数更新。

对于VDGC-ER 模型的ELBO 项，如式（10）所示，逐项基于蒙特卡洛采样及重构策略进行估计。具体地，式（10）等式右边第一项估计为：

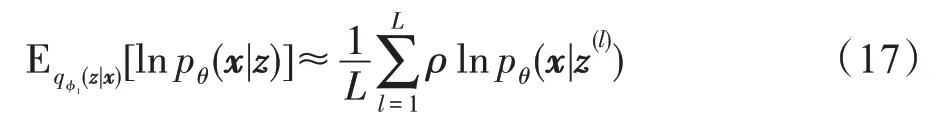
其中，ρ表示超参数，z(l)表示蒙特卡洛第l次采样时的隐变量样本，由重参数化技巧获得：

分析式（21）易知先验项具有反聚类的作用：在最小化式（21）时，会使熵变大，促使趋近于均匀分布，导致每个样本x对GMM 中组件的选择都是随机的，失去了聚类的效果。这个问题可以通过样本熵正则化项来减缓。

对于式（10）等式右边第三项估计为：

3) 为了保证阀门泄漏等级达到Class VI，该阀门采用金属支撑的软密封结构，即在软性材料的旁边有金属限位平面。阀芯软密封环通过螺纹压紧在阀芯体上，阀芯和阀座之间通过斜锥面密封，有效密封宽度4 mm左右。该阀门阀芯头部带18 mm左右延伸段，该结构优点：

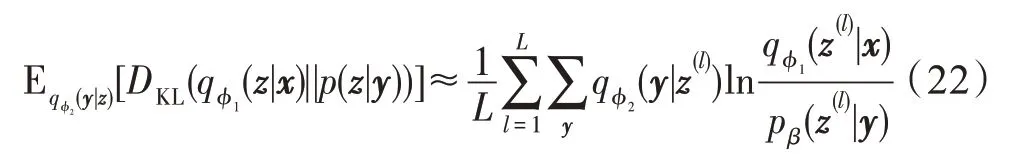
式（22）为聚类的关键项，具体地，对于某个样本x，当为概率分配中的最大值时，由于KL散度的约束，使样本x更倾向于从p(z|y=k)中产生。

最后，结合式（17）、式（21）与式（22），对于单样本点x，VDGC-ER 模型的证据似然下界估计为：

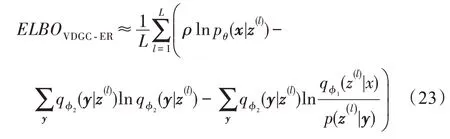
其中，z(l)表示第l次蒙特卡洛采样得到的隐向量样本。

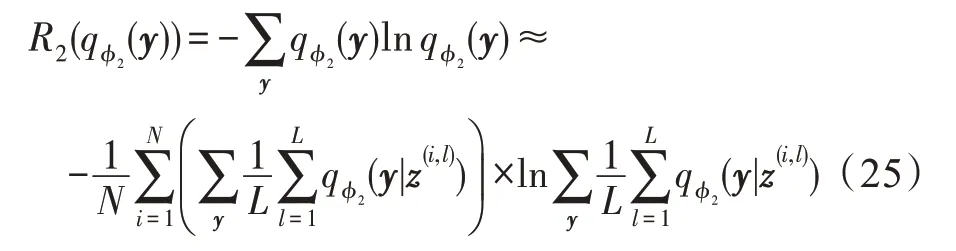
最后将式（23）～式（25）代入式（15）得到最终的目标函数，再采用随机梯度下降法来对参数{θ,ϕ,β}进行更新。

图2 表示VDGC-ER 模型训练时前向传播过程的网络框架图，具体包括三部分：f1、f2、f3。分别计算概率分布的参数。具体地，对于单样本x，首先经过f2得到概率分布的均值和方差；然后经过重参处理，得到隐向量样本z；最后z经过f1得到重构数据x′，经过f3得到概率分布的参数。对于概率分布p(z|y)的参数β，它在随机初始化后作为模型的可训练参数参与模型优化目标的计算。针对优化目标式（16），结合前向传播与反向传播，利用随机梯度下降法对参数ϕ、θ与β进行更新。

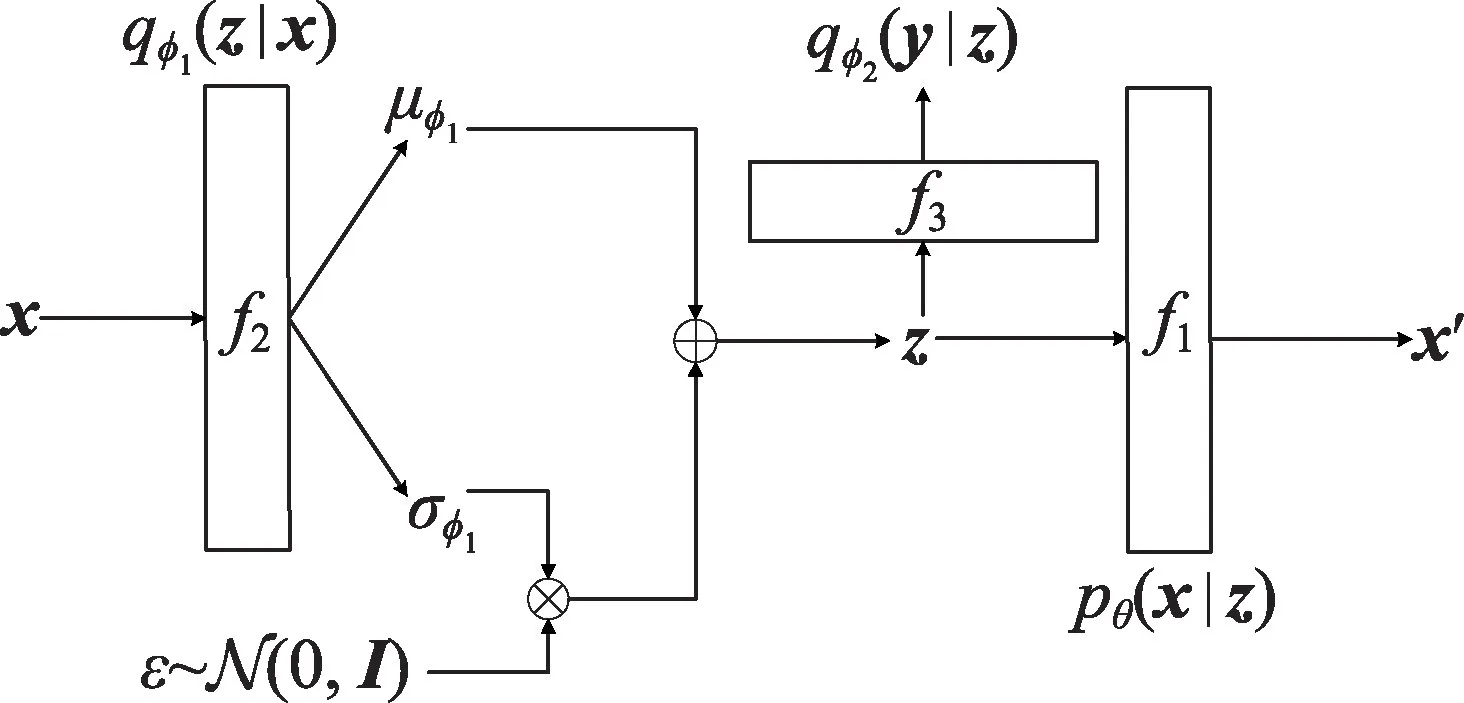
图2 VDGC-ER 的网络框架Fig.2 Network framework of VDGC-ER

3 实验

本章设计了对比实验来证明VDGC-ER 模型的聚类性能，同时，考虑生成模型本身的特性，验证模型生成样本的能力。具体包括3 个实验：实验1，分析正则化项对聚类精度产生的影响，并确定正则化项超参数；实验2，在不同数据集上通过对比实验验证VDGC-ER 算法的聚类性能；实验3，分析VDGC-ER模型生成样本的能力及数据隐空间的可视化。

本文采用的数据集包括MNIST 数据集[18]、REUTERS数据集[19]、REUTERS-10K数据集[19]、HHAR数据集[20]。具体地，MNIST 是标准的手写数字识别数据集，包括10 种不同的数字（0～9）。REUTERS 与REUTERS-10K 是两个新闻数据集，包括4 类数据：企业/工业数据、政府/社会数据、市场数据和经济数据。HHAR 是人体活动检测数据集，包括6 类数据：走路、上楼、下楼、坐着、站着、躺着。4 个数据集的其他详细信息如表1 所示。

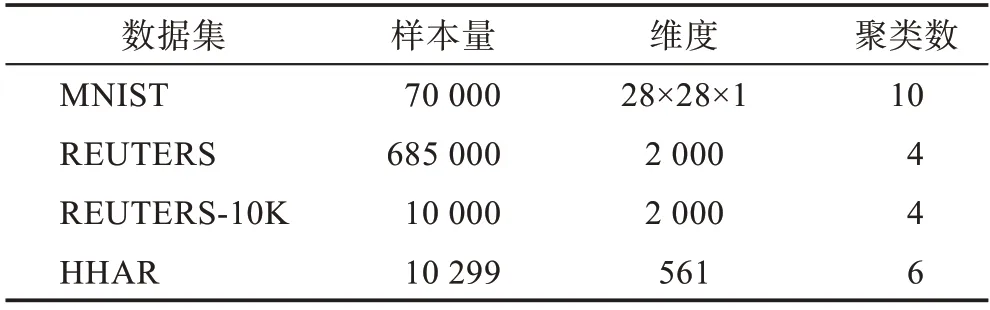
表1 数据集的详细信息Table 1 Detailed information of datasets

对比实验的模型包括：K-means 方法[2]、GMM[3]、VaDE模型[4]、DEC模型[8]、MIXAE模型[9]、AAE模型[12]。

3.1 正则化项对模型聚类精度的影响

本节在MNIST 数据集、HHAR 数据集、REUTERS数据集和REUTERS-10K 数据集上，通过设置不同样本熵正则化项系数η和聚合样本熵正则化系数γ的值，分析两个正则化项对模型聚类精度产生的影响。针对VDGC-ER 模型，首先固定γ=0，设置不同的η值，分析样本熵正则化项对VDGC-ER 模型的影响；然后固定η=0，设置不同的γ值，分析聚合样本熵正则化项对VDGC-ER 模型的影响。实验结果如表2 和表3 所示。

根据表2 可知，对于样本熵正则化项，当对应的正则化系数η取值逐渐增大时，VDGC-ER 模型在数据集上的聚类精度先增加后减少。聚类精度上升阶段：随着η取值不断增大，样本对应的隐向量z归属于某一类别的置信度逐渐增大，将软分类近似转换为硬分类，即变分分布qϕ2(y|z)趋向于独热编码。聚类精度下降阶段：该阶段模型陷入局部最优解，即对于不同类别的数据，VDGC-ER 模型倾向于将它们归属到同一聚类簇中，且随着η不断增大，局部最优解问题越来越明显。

表2 样本熵正则化项对聚类精度的影响Table 2 Influence of sample-wise entropy regularisation term on clustering accuracy

根据表3 可知，对于聚合样本熵正则化项，当对应的正则化系数γ取值逐渐增大时，VDGC-ER模型在MNIST 数据集和HHAR 数据集上的聚类精度有上升趋势，总体相对稳定在一个较高的值，而在REUTERS数据集和REUTERS-10K 数据集上聚类精度先上升再下降，且下降的趋势较为明显。聚类精度有上升现象表明VDGC-ER 模型强制数据集均匀分布在各个聚类中心附近，达到聚类样本均衡状态后，聚类精度将相对稳定。聚类精度显著下降是由于样本不平衡导致的，因此聚合样本熵正则化项对数据集的选择较为敏感。

表3 聚合样本熵正则化项对聚类精度的影响Table 3 Influence of batch-wise entropy regularisation term on clustering accuracy

本实验也反映出由先验项所导致的反聚类现象。在表2 中，考虑η取值从0 到1.0 的过程，先验项慢慢被抵消。在η=1.0 时，先验项被完全抵消，此时发现在MNIST 数据集、HHAR 数据集、REUTERS 数据集和REUTERS-10K 数据集上分别取到了0.11 个百分点、3.10 个百分点、1.75 个百分点和4.00 个百分点的提升。

综上，通过实验分析可知，样本熵正则化项和聚合样本熵正则化项均可提升VDGC-ER 模型的聚类精度，其中样本熵正则化项通过提升隐向量样本z的聚类置信度来提升聚类精度，聚合样本熵正则化项通过使聚类样本均衡来提升聚类精度。最后通过实验说明了先验项的反聚类的作用。

3.2 模型聚类性能对比实验

本节在MNIST、REUTERS、REUTERS-10K及HHAR数据集上，对比VDGC-ER、GMM、K-means、AAE、DEC、MIXAE 与VaDE 模型的聚类精度。

具体地，在4个数据集上的基本实验参数有：优化器为Adam[21]，学习率0.001，迭代次数为epochs=50，批量样本大小B=128，隐向量维度M=32，蒙特卡洛采样次数L=1，超参数ρ=2.5。参数K设置为数据集的类别个数。在MNIST 数据集中，推理模型和生成模型均采用卷积神经网络，分类器和先验层均使用全连接网络，而在其他3个数据集上，全部使用全连接网络。样本熵正则化系数η在MNIST 数据集、REUTERS数据集、REUTERS-10K数据集及HHAR数据集上的值分别为2.7、3.8、3.8 与3.8。聚合样本熵正则化项系数γ在4个数据集上的值均为6.0。

聚类性能的评价指标遵循了DEC 模型中的方法，即VDGC-ER 模型的聚类精度定义为：

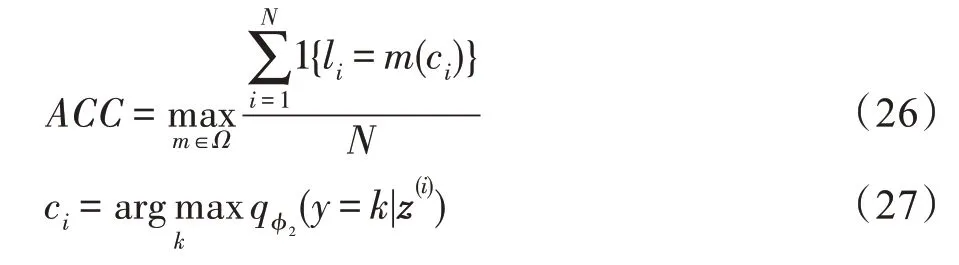
其中，N为总样本数，li表示第i个样本的真实标签，ci为第i个样本在概率分配中的最大值的索引，由分类器计算得到。m∈Ω表示真实标签和聚类标签之间的映射关系，Ω为映射关系的集合，最佳映射关系可由Hungarian 算法[22]给出。

对比实验的结果如表4所示，可以看出VDGC-ER模型在相同数据集条件下，相较于其他模型，聚类精度都达到了最高。具体地，VDGC-ER 在MNIST、REUTERS、REUTERS-10K 和HHAR 数据集上，相较于对比模型中聚类精度最高值分别有1.44 个百分点、7.83个百分点、5.12个百分点和1.30个百分点的提升。

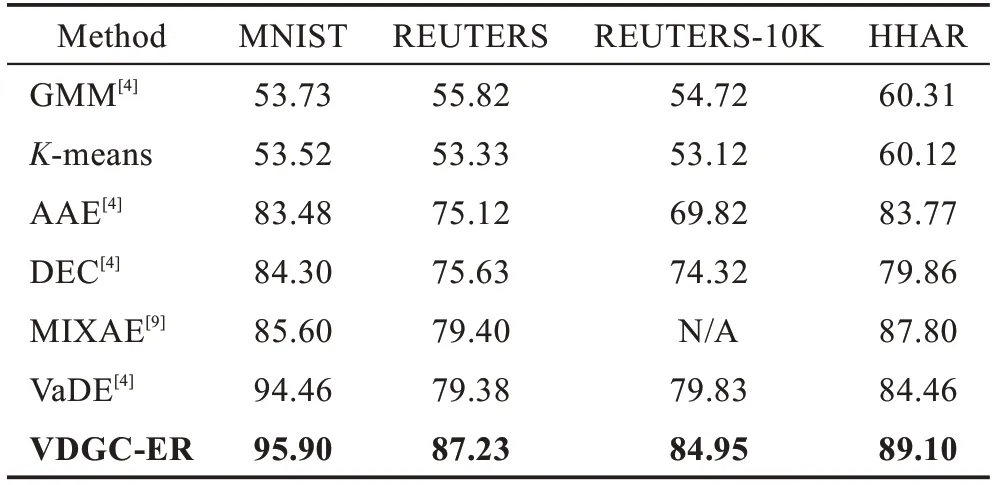
表4 不同数据集上不同模型的聚类精度的对比Table 4 Clustering accuracy comparison of different models on different datasets 单位：%

另外，通过结合实验1 和实验2 发现，当将两个正则化项一起使用，并设置合适η和γ值时，得到的效果总比单独使用样本熵正则化项的效果要好，这说明聚合样本熵正则化项可以改善由样本熵正则化项引起的局部最优解问题。关于超参数的值的选取，具体地：对于超参数ρ，它控制着训练过程中重构误差项的权重，推荐取值为[2，3]；对于超参数η和γ，它们控制着正则化强度，考虑两个正则化项之间的关系，推荐在[0.5，10.0]这个区间内进行网格搜索以确定最佳的η和γ。

通过实验分析可知，VDGC-ER引入两项正则化项后，模型在聚类性能上有明显的提升，这也表明，正则化项可以使VDGC-ER模型更加稳定，聚类结果更优。

3.3 模型的生成能力与可视化隐空间

本节在MNIST 数据集上验证了VDGC-ER 模型生成样本的能力，并且利用VDGC-ER 模型对MNIST和HHAR 数据集的隐空间进行了可视化。

为了验证VDGC-ER 模型的生成能力，本实验在MNIST 数据集上分别使用VAE、VaDE 和VDGC-ER模型来生成图片。具体地，对于VAE 模型来说，模型训练好后直接从标准正态分布中采样来生成图片。对于VaDE 和VDGC-ER 模型来说，模型训练好后从GMM 中的每个组件中随机采样来生成图片。最终得到的结果如图3 所示。

图3（a）表示VAE 随机生成的样本，生成的图像显示VAE 生成的图像比较模糊，并且没有聚类的能力。图3（b）和图3（c）中每一行代表从每个聚类簇中生成的图片，证明VaDE 和VDGC-ER 不仅可以生成质量较清晰的图像，而且具有很好的聚类能力。值得注意的是，观察图3（b）中方框圈出来的数字，它们相对较为模糊而且与它们生成的数字与真实标签相比存在一定的误差，VDGC-ER 模型则没有，可视化实验也表明VDGC-ER模型的聚类性能要优于VaDE模型。

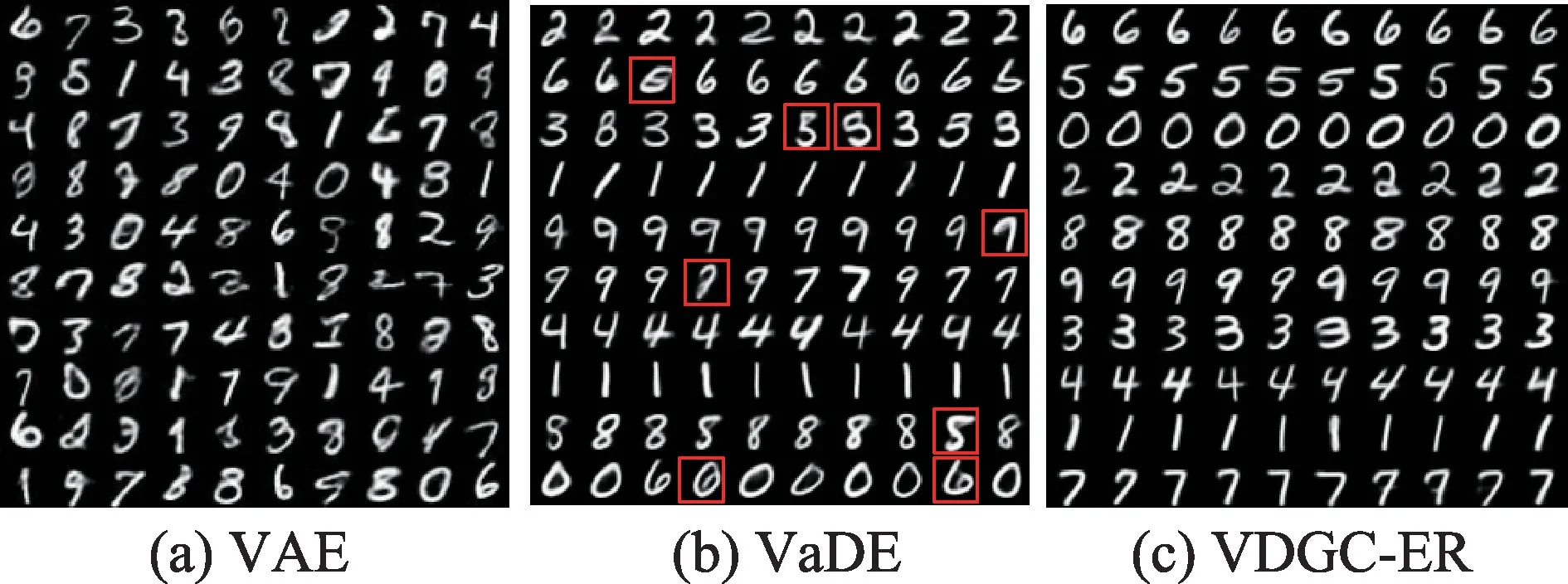
图3 用VAE、VaDE 和VDGC-ER 生成的数字Fig.3 Digits generated by VAE,VaDE and VDGC-ER

本文进一步对VDGC-ER 模型在MNIST 数据集和HHAR 数据集聚类后的隐空间进行可视化。对于训练后的VDGC-ER 模型，随机选取了2 000 个样本点，利用t-SNE 算法[23]将隐向量z从32维降成2维，并在二维空间进行可视化表示，如图4 所示。在图4 中，每一种颜色代表一个聚类簇，例如在MNIST 数据集中，每一个簇表示一类数字。由图4 可知，在MNIST数据集和HHAR 数据集上，类别个数与对应隐空间中簇的个数是一致的，且簇与簇之间有明显的分离现象，说明VDGC-ER模型具有非常好的聚类效果。

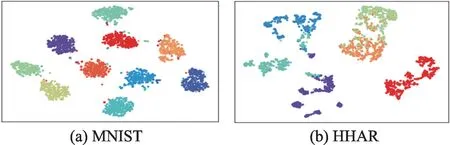
图4 VDGC-ER 在两个数据集上的隐空间可视化Fig.4 Visualization of latent space on MNIST and HHAR datasets using VDGC-ER model

通过实验分析，VDGC-ER 模型不仅具有良好的生成能力，而且通过可视化训练数据集的隐空间，验证了VDGC-ER 模型具有非常好的聚类能力。

4 结论

本文提出熵正则化下的变分深度聚类模型，使用VAE 模型作为基础框架，利用GMM 为数据的隐空间进行先验建模，通过引入样本熵正则化项与聚合样本熵正则化项来约束隐空间中的聚类分配和样本生成任务，最后采用蒙特卡洛法及重参策略来求解优化问题。样本熵正则化项通过约束离散样本点近似后验概率分布提高聚类精度，聚合样本熵通过约束离散空间的分布避免局部最优；同时基于生成模型的聚类方式可以使模型具有较好的样本生成能力。理论分析与实验结果表明，VDGC-ER 模型的熵正则化项不仅可以生成高质量的样本，而且可以显著提升聚类精度。