基于平均增益模型的模拟退火算法计算时间分析
周竹连,周珍胜,冯 乐,汤华椿,吴 磊,谭 棉
(1.贵州民族大学 数据科学与信息工程学院;2.贵州民族大学 贵州省模式识别与智能系统重点实验室,贵州 贵阳 550025)
0 引言
模拟退火算法由Metropolis 等[1]首次提出,并广泛应用于组合优化领域,目前在神经网络超参数优化、神经网络结构优化、组合优化、部分机理模型难以建立的黑箱优化问题和多目标优化问题方面都进行了一定研究[2-8]。但关于模拟退火算法理论分析,尤其是计算时间分析的研究不多,因此模拟退火算法计算时间分析是如今国内外学者关注的热点话题[9]。
近年来,关于模拟退火算法设计的研究已经有了一些成果,例如,常媛等[9]对模拟退火算法、遗传算法和启发式算法在钢筋下料优化问题上进行比较,不同算法都具有各自的特点;傅文渊等[10]将模拟退火算法与布朗运动相结合,提高了算法的搜索速度与稳定性;张德富等[3]将模拟退火算法与启发式算法相结合,提出了混合模拟退火算法,并验证了该算法在三维装箱问题上的有效性。此外,结合遗传算法,Yi 等[4]改进了模拟退火算法,有效减少了立体车库调度优化问题的优化时间;Guo 等[5]基于模拟退火算法和遗传算法设计了一种混合算法,在机械系统上提高了摩擦力参数识别精度;Fan 等[6]将模拟退火算法与免疫机制加入遗传算法中以解决图像聚类问题,并解决了遗传算法易陷入局部最优的问题;Yu 等[7]将改进的遗传算法和模拟退火算法用于测试数据集的生成,实验结果表明其效果优于遗传算法;Jia 等[8]改进了模拟退火算法,并将其用于在大数据集中搜索离群数据,有效提高了搜索速度;李元香等[11]将动力系统理论引入模拟退火算法的理论分析,通过建立动力系统模型,分析了模拟退火算法的收敛性。此外,其将弛豫模型引入模拟退火算法时间复杂性分析,设置动态马尔科夫链长度的动力系统模型分析了模拟退火算法的收敛性,并给出了模拟退火算法的停止准则[12]。李元香等[13]还针对模拟退火算法的运行机制提出动态自适应退火温度设置方法。综上所述,模拟退火算法在工业应用与理论研究等方面都有了一定基础,但主要针对算法设计,关于模拟退火算法计算时间分析的研究仍然较少。因此,关于该领域需要作进一步研究。
另外,国内外学者在算法计算时间分析方面也进行了研究,例如,He 等[14]提出漂移分析理论,并严格分析了进化算法在采用不同变异算子和精英选择算子时种群规模对计算时间的影响[15];Yu 等[16]提出转换分析法,该方法主要讨论了不同变异算子下进化算法的期望运行时间;黄翰等[17]建立一种等态关系模型与强/弱态偏序关系模型,分析了进化算法与不同变异算子的关系;冯夫健等[18]提出等同关系模型,该模型分析了不同选择算子和不同变异算子进化算法的性能对比关系;张宇山等[19-20]提出平均增益模型,以球函数为例分析了进化算法的平均计算时间,并提出停时理论模型来分析进化算法的首达时间,其还在平均增益模型上加入鞅论和停时理论,分析了连续型演化算法的平均首达时间上界;Huang 等[21]基于平均增益模型提出一种求解连续优化问题的进化算法运行时间实验方法。总体而言,目前关于算法理论的研究主要集中在计算时间分析与收敛性分析上,而首达时间是计算时间分析中的一个重要概念,指算法首次找到最优解所花费的运行时间(迭代次数)。
本文将以首达时间作为分析工具展开研究,主要目的在于建立模拟退火算法的平均增益模型,并加以验证,通过理论分析与数值实验的方式验证平均增益模型在模拟退火算法上的可行性。因此,基于平均增益模型推导模拟退火算法的计算时间上界,并在变异算子满足正态分布与均匀分布时分析线性函数上模拟退火算法的期望首达时间。数值实验结果验证了理论推导的正确性,并且理论分析与数值实验结果一致,表明平均增益模型应用于模拟退火算法是可行的。
1 模拟退火算法平均增益模型
1.1 模拟退火算法随机过程
模拟退火算法的原理来源于固体退火,是一种基于概率的算法[1]。该算法的思想是从一个较高的初始温度开始,以一定速率降温,直到温度降到终止条件为止。在每个温度下进行搜索,每轮搜索以特定规则产生新解,并按照Metropolis 准则接受新解。假设T0表示初始温度,任取初始解,在每个温度下迭代L轮,也称为Metropolis 链长。具体模拟退火算法流程如下:
算法1模拟退火算法流程

根据算法1 可知,步骤6 表示当前解Yt通过随机扰动产生一个新解Ynew,其中f(Yt)为Yt的代价函数;步骤10-16表示按照Metropolis 准则判断是否接受新解。如果满足终止条件,则输出最优解,结束程序。否则按衰减函数衰减后返回步骤3。
设(Ω,U,)是概率空间,映射f():Ω →Rn称为n维的随机变量[20]。本文考虑找到一个全局最优解x*∈Ω,使得目标函数值最小f(x*)=minf()。
定义1设是一个随机过程,当任意的t≥0,T≥Tend,满足≥0 成立,且存在目标精度ε>0,那么模拟退火算法的首达时间为hε=min
定义1 表明,模拟退火算法的首达时间是在目标精度ε下得到的,首达时间的期望表达为E(hε),称为期望首达时间。模拟退火算法的首达时间表示算法找到目标解的最小降火次数。
1.2 模拟退火算法计算时间分析
下面给出模拟退火算法的平均增益定义:

引理1 给出了模拟退火算法的平均增益模型求解期望首达时间上界的公式。基于引理1,将以线性函数为个案讨论模拟退火算法的计算时间。
2 模拟退火算法个案平均计算时间分析
本节将运用模拟退火算法的平均增益模型分析线性函数的期望首达时间上界。
2.1 标准正态分布条件下模拟退火算法计算时间分析
在算法1 的基础上加入变异算子与选择算子,改进的算法描述如下:
算法2基于变异算子的模拟退火算法



定理2在线性函数f(X)上,最小值为W0时,模拟退火算法的期望首达时间上界如下:

假设函数f的起始函数值为W0+ncW0,则=ncW0,c=Wi表示xi的权重,根据定理2,期望首达时间上界推导为:
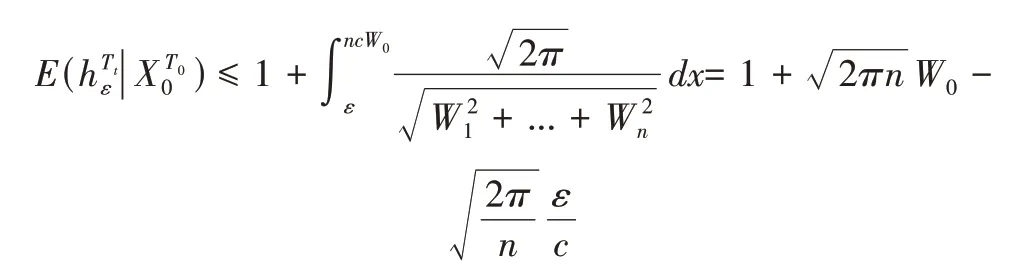
证毕。
由定理2 可得模拟退火算法在变异算子满足标准正态分布时的上界为下一节将分析变异算子为均匀分布时的计算时间上界。
2.2 均匀分布条件下模拟退火算法计算时间分析


3 数值实验分析
本节实验采用变异算子为N(0,1)和来验证定理2与定理4的准确性。
3.1 变异算子为N(0,1)的计算时间分析



Table 1 Comparison of expected first hitting time and theoretical upper bound of simulated annealing algorithm表1 模拟退火算法期望首达时间与理论上界比较
图1 显示了当变异算子为N(0,1),在n=10 与n=20时的迭代过程。由图1 可以看出,存在多次迭代得到的目标函数值相同的情况,表明模拟退火算法在迭代过程中,当前解优于新解,并且Metropolis 准则没有发生,导致多次迭代下得到的最优函数值相同,整个优化过程呈递减趋势,直到满足终止条件为止。从图1(a)和图1(b)的迭代次数得出,随着n的增大,迭代次数也增加,数值实验结果与理论分析一致。
3.2 变异算子为U(-,)的计算时间分析


Fig.1 Optimization process of function values图1 函数值优化过程

Table 2 Comparison of expected first hitting time and theoretical upper bound of simulated annealing algorithm表2 模拟退火算法期望首达时间与理论上界比较
4 结语

Fig.2 Optimization process of function values图2 函数值优化过程
本文针对模拟退火算法的首达时间理论分析问题,建立模拟退火算法的平均增益模型。基于平均增益模型求解模拟退火算法采用标准正态分布变异算子和均匀分布变异算子时在线性函数上的期望首达时间,并通过数值实验进行验证,计算时间与问题规模n有关。理论分析结果表明,当n越大时,期望首达时间越长,且数值实验结果与理论分析相吻合。此外,通过理论分析与实验论证了平均增益模型能够用于分析模拟退火算法计算时间。未来工作中,将应用模拟退火算法的平均增益模型建立计算时间对比模型,继续深入探索与分析模拟退火算法计算时间。

