转角半导体过渡金属硫族化物莫尔超晶格中的新奇物态*

汤衍浩

(浙江大学物理学院,量子信息交叉中心,省重点量子技术实验室,杭州 310063)

通过转角或晶格失配构造莫尔人工超晶格,可以对二维材料的能带结构进行有效调控并产生平带,为研究量子多体物理提供了全新的平台.转角过渡金属硫族化物(TMDs)半导体莫尔超晶格中的平带存在于较大的转角范围,并且具有自旋-能谷互锁的能带结构以及优异的光学特性,受到了广泛的关注.本文聚焦于转角TMDs半导体,介绍了近年来实验上发现的多种新奇物态,包括莫特绝缘态、广义维格纳晶体、非平庸拓扑态、莫尔激子等;还进一步讨论了对这些新奇物态的调控及其机制,并展望了莫尔超晶格这一新兴领域未来的研究方向.

1 引言

近年来,莫尔超晶格的研究取得了极大的发展,已经成为凝聚态物理中最为活跃和重要的研究方向之一.莫尔纹很早就被人们所认识,其可以通过两种周期性的图案干涉叠加而产生,具有类似“拍频”的新奇视觉效果.该现象最早在中国被用于纺织,并在艺术和力学测量等领域有着一定应用[1,2].近二十年来兴起的范德瓦耳斯材料及其异质结[3−11],让我们有机会可以从微观的层面重新审视这一人工超晶格结构.范德瓦耳斯材料是一种层内原子通过化学键结合,而层与层之间通过范德瓦耳斯力结合的二维材料.当两层具有不同晶格常数或者不同转角的原子级厚度的二维材料被堆叠起来,可以形成微观尺度上的莫尔纹.这一现象在早期的石墨烯块材的扫描隧道显微镜(STM)实验中已被报道[12,13].不同于宏观的莫尔纹仅仅产生视觉上的效果,基于二维材料的莫尔纹可以让材料在原子尺度上发生耦合,从而产生出远不同于原本材料的物理性质[14−17].

莫尔超晶格对二维材料的能带结构可以产生显著的调制.2009 年,Andrei 课题组[18]利用化学气相沉积(CVD)生长双层石墨烯,通过STM 发现在具有一定相对转角的双层石墨烯中存在AA和AB/BA 堆叠形成的超晶格结构,并发现狄拉克点附近产生了新的范霍夫奇点.2010 年,Dean 等[11]利用干式转移,将六方氮化硼(hBN)作为电介质材料包裹住石墨烯,使其免于衬底和外部的影响,从而极大地提高了石墨烯器件质量.研究者控制hBN 和Graphene 的转角,成功制备出hBN-Graphene 莫尔超晶格,通过电输运发现体系在莫尔布里渊边界打开了能隙,并且当强磁场使得磁通量的密度和莫尔晶胞可比拟时,出现了Hofstadter 蝴蝶效应[19−22].

莫尔超晶格更为重要的意义在于,通过对能带的调控可以产生平带,结合二维材料易调控的优势,为强关联物理和量子模拟的研究提供了一个全新的实验平台.理论工作者预言在1.05°转角附近的双层石墨烯中,电子能量随动量的线性色散被层间相互作用“完美”抑制,从而产生平带,而这一角度也被称为魔角[14,15].由于石墨烯中电子能量色散较大,平带只存在于很小的转角范围(约为0.1°).2018 年是莫尔超晶格领域的一个重要转折点,Jarillo-Herrero 课题组通过“撕裂和旋转(tearand-rotate)”技术精准地控制双层石墨烯之间的转角,结合电学掺杂调控,在1.1°转角的双层石墨烯中发现了关联绝缘态[10]和超导态[9].该研究证明了莫尔超晶格在调控乃至构筑量子新奇物态方面的巨大潜力,从而掀起了一股莫尔超晶格“淘金”浪潮.多种基于石墨烯的莫尔超晶格体系及其中的新奇物态被发现,例如三层石墨烯-BN 体系[23,24]、转角双层石墨烯-BN[25,26]、转角双层-双层石墨烯[27−29],转角三层石墨烯[30,31]等超晶格体系,以及其中的轨道磁性[26]、量子反常霍尔效应[25]、向列态[32]、超导重入现象[30]等新奇物理现象.有趣的是,在非转角的双层和三层石墨烯中,研究者也在更低的转变温度发现了轨道磁性和超导[33−35].

相比于石墨烯体系,基于半导体过渡金属硫族化物(TMDs)的莫尔超晶格因为其迥然不同的物理特性,也受到了极大关注.首先,转角半导体TMDs中的平带存在于很大的转角范围(比魔角双层石墨烯大了约1 个量级)[17,36,37],极大提高了器件的重复性.其次,转角半导体TMDs 中的电子相比于转角石墨烯具有更高的空间局域性[17,36],其Wannier波函数半径远小于莫尔晶格常数,因此可以用于模拟Hubbard 模型等晶格模型.最后,半导体TMDs具有丰富的激子态以及很好的光学性质[38,39],不仅为探测强关联物态提供新的途径[40−43],还可以用来研究玻色子强关联物理[44].

后文将介绍半导体TMDs 及其莫尔超晶格的物理特性,讨论转角半导体TMDs 中实验上发现的新奇物态以及新颖的调控机制,最后探讨莫尔超晶格这一新兴领域未来的研究方向.

2 转角半导体TMDs

2.1 单层半导体TMDs

半导体TMDs 具有六方晶格结构,化学式为MX2,其中M 为过渡金属(例如W,Mo),X 为硫族化物(例如S,Se,Te).单层TMDs 中的过渡金属原子被两层硫族化物原子包裹.当半导体TMDs块材被剥离至单层,能带结构由间接带隙转变为直接带隙[6,7],价带顶和导带底位于布里渊区K和K′处.由于空间反演对称性破缺和自旋轨道耦合,自旋在K和K′处发生劈裂,导致能谷位置和自旋朝向锁定[39].基于这种能带结构,利用光学方法可以选择性地激发K(K′)处的电子,或者读取K(K′)处电子的占据信息.同时,由于单层TMDs 中库仑屏蔽效应被极大地减弱,并且K(K′)处的光学跃迁均主要来自于过渡金属的d 轨道,TMDs 中的激子具有极大的激子结合能和极强的光与物质相互作用[38].这些特点使得半导体TMDs 成为能谷电子学的潜在候选者[38,45].

2.2 转角TMDs 莫尔超晶格

2.2.1 莫尔周期势

通过堆叠两层具有不同晶格常数或角度的TMDs 单层,当转角处于0°附近,可以形成具有AA 和BXM(MX)晶格位的周期性结构,当转角处于60°附近,可以形成具有AB 和BMM(XX)晶格位的周期性结构(图1(a),(b)).其中,在AA 晶格位上,上下两层的M 和X 原子相互重叠;在AB 晶格位上,上层的M 和X 原子分别和下层的X 和M 原子相互重叠;在Bij位上(i=M,X;j=M,X),上层的i原子和下层的j原子重叠.为方便讨论,默认情况下主要讨论0°附近的转角TMDs.莫尔超晶格产生的莫尔周期势,将使得能带发生折叠,从而形成一系列的莫尔能带,并且能带宽度被角度所调制(图1(c),(d)).在小转角和小晶格常数差的情况下,莫尔超晶格的晶格常数aM≈其中a是TMDs 的晶格常数,δ是两层TMDs 的晶格常数失配比,θ是两层之间的转角.莫尔周期势主要来源于两层TMDs 中的电子在不同晶格位有着不一样的耦合强度[17,46].此外,由于晶格重构效应,TMDs 莫尔超晶格中存在周期性的应变,例如研究者在转角TMDs 同质结[47]和异质结[48]中,通过STM 观测到了上下起伏波纹状的结构.这种应变将进一步调制单层TMDs 中能带结构,从而调制莫尔周期势.

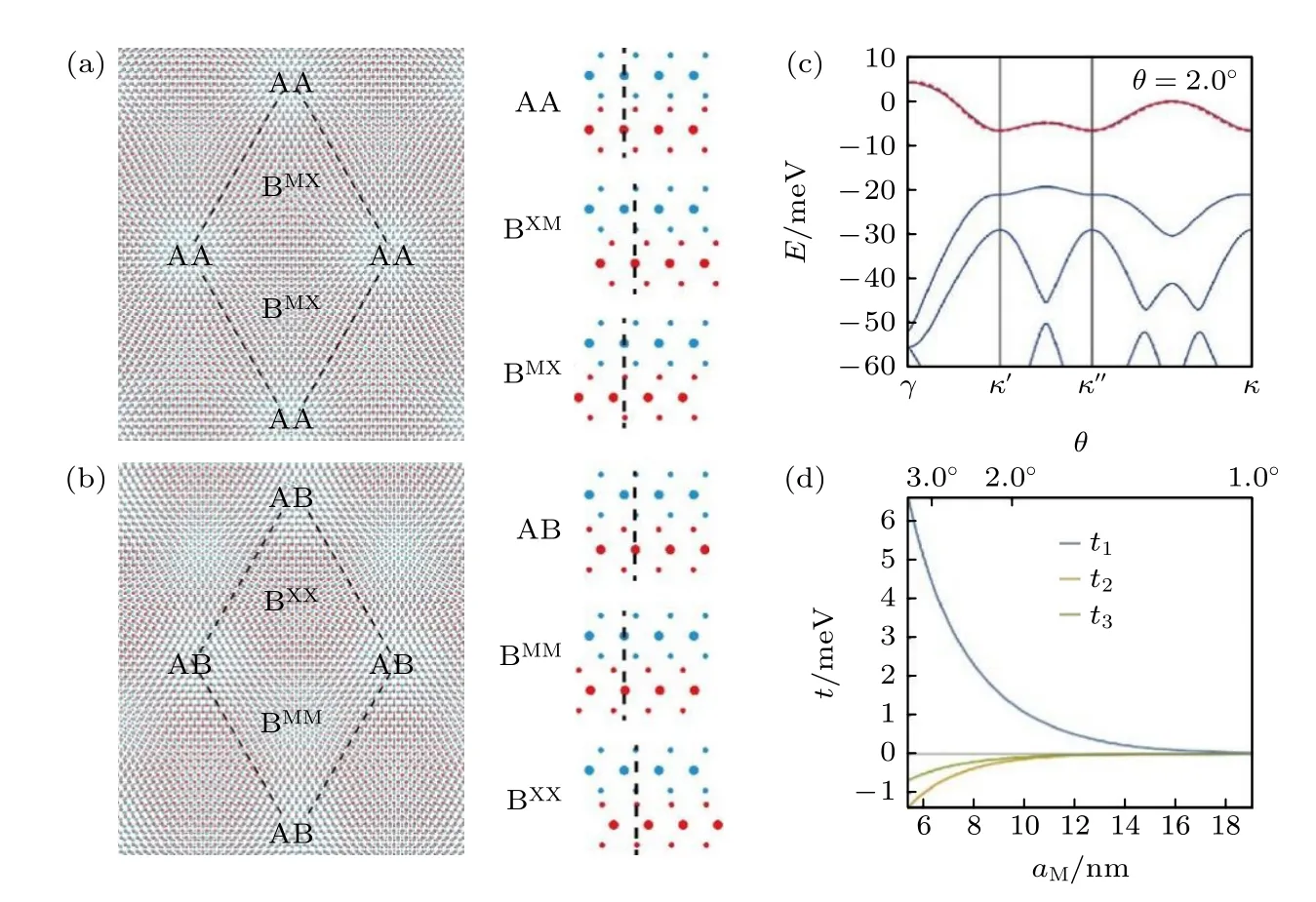
图1 转角TMDs 的晶格和能带结构0°转角 (a)和60°转角 (b) TMDs 异质结的晶格结构示意图;(c)转角WSe2/MoSe2 的能带图[17];(d)不同晶格位之间跃迁的动能随莫尔晶格常数的依赖关系[17]Fig.1.Crystal structure and band structure in twisted TMDs: The crystal structure in 0° (a) and 60° (b) twisted TMDs heterobilayer;(c) the moiré band structure of low-energy electrons in 2° twisted WSe2/MoSe2 heterobilayer[17];(d) the kinetic energy of electrons hopping between different moiré sites as a function of the moiré lattice constant[17].

2.2.2 角度缺陷(angular disorder)

与传统材料不同,莫尔超晶格的物理性质依赖于转角,从而具有一种新的缺陷种类—角度缺陷.转角TMDs 从材料构成上可以分为莫尔同质结和莫尔异质结.在莫尔同质结中,由于δ=0,莫尔晶格常数对于转角非常敏感.虽然莫尔同质结可以通过tear-and-rotate 的方式精确控制层间转角,但是当两层TMDs 堆叠在一起时,转角往往会发生不可控的偏移,从而使得莫尔同质结的角度空间均匀性较差[49].而在莫尔异质结中,这种角度缺陷可以很好地被抑制[48].莫尔异质结中的两层TMDs 的晶轴朝向可以通过测量极化方向依赖的二次谐波来表征,通常精确度为±0.5°[40].当转角TMDs 异质结存在较大的晶格失配时,转角的偏差对莫尔晶格常数的影响将非常小(例如,MoTe2/WSe2晶格失配约为8%,转角从0°变为1°,只会让莫尔晶格常数改变约2%[50,51]),因此莫尔异质结通常具有更好的空间均匀性和器件的可重复性.

2.2.3 低能量电子空间局域性

与魔角双层石墨烯中平带或者强关联效应只存在于魔角附近非常小的转角范围(1.1°±0.1°)不同[9,10],转角半导体TMDs 中莫尔能带宽度随着转角变大而单调增大[17,36],并且在较大的转角范围内都存在强关联效应.例如,研究者在转角为5°的双层WSe2中通过电学输运测量仍然观测到了关联电子态[37].同时,转角TMDs 中的低能量电子具有较好的空间局域性.研究者通过第一性原理的电荷密度泛函理论计算发现了3.5°转角的双层MoS2中,低能量空穴局域在MX 和XM 位[36],并得到了STM 实验的进一步验证[47].值得指出的是,空穴局域的晶格位置强烈依赖于晶格重构效应,如果不考虑晶格重构,空穴将局域在MM 位[36].

2.2.4 理论模型

由于低能量电子的空间局域化,研究者提出了基于转角半导体TMDs 模拟晶格模型的多种方案.转角双层TMDs 异质结中的价带存在巨大的自旋-轨道劈裂,可以用于模拟三角晶格中单轨道的Hubbard 模型,并发现在莫尔能带半填充和其他分数填充下可能存在新奇关联绝缘态和超导态[17];转角双层TMDs 同质结中存在双轨道的低能量空穴,可以用于实现Kane-Mele 模型,即存在具有时间反演对称性不变的二维拓扑绝缘态[52,53].转角单层-双层TMDs 异质结同时存在空间局域电子和巡游电子,可以用于实现Kondo 晶格模型[54];转角TMDs 异质结中还存在空间局域化的层间莫尔激子,可以用于实现Bose-Hubbard 模型[44].

3 转角半导体TMDs 中的关联电子物态

3.1 莫特绝缘态(Mott insulator)及其光学探测

当体系的每个晶格上有一个电子(填充因子为1)并且电子在同一晶格位上的库伦相互作用(U)远大于能带宽度(W),电子将无法自由移动,从而形成莫特绝缘态[55],见图2(a).多个实验课题组各自通过不同的探测手段,在转角半导体TMDs中发现了莫特绝缘态或关联绝缘态[37,40,42,43].

3.1.1 转角TMDs 异质结

Wang 课题组[42]设计和制备了一种特殊的器件结构,0°转角的WSe2/WS2被分为两个区域(有或没有顶端栅极).研究者利用TMDs 和金属肖特基接触形成的极大的接触电阻,使电荷在顶栅高频电压调制下只能在转角TMDs 的两个区域之间流动,并结合TMDs 光学性质对于电荷浓度的依赖关系,标定了转角WSe2/WS2在不同电荷浓度下的等效电阻和电容.研究发现,当每个莫尔晶胞填充的空穴为1 时,等效电阻和电容分别呈现为极大和极小值,证明了体系处于莫特绝缘态.Mak 和Shan 课题组[40]设计和制备了60°转角的WSe2/WS2的双栅极器件,通过测量莫尔激子反射谱发现,当莫尔晶胞填充因子为1 时,莫尔激子的反射强度增强,反映了体系对于莫尔激子的屏蔽作用减弱,证明了体系处于莫特绝缘态.这一结论进一步被两端法输运测量验证—电阻在填充因子为1 处增大了两个数量级.同时,研究者利用TMDs 中光学跃迁的能谷选择性,测量了磁化率随温度的依赖关系,从而发现莫特绝缘态具有反铁磁相互作用.值得指出的是,这一结果和Hubbard 模型的理论相自洽[56],为利用转角TMDs 研究Hubbard 模型打下了实验基础.理论研究者还指出WSe2/WS2中的莫特绝缘态很有可能是一种电荷转移绝缘态,即莫尔晶胞中填充的第2 个电子和第1 个不在同一晶格位上[57],该图像仍有待STM 实验的检验.

3.1.2 转角TMDs 同质结

Dean 课题组[37]在转角为4°—5°的双层WSe2中通过电学输运测量发现了关联绝缘态.由于在如此大转角的情况下,电子之间的库仑相互作用约为30 meV,最低莫尔能带宽度约为60—80 meV,所观测到的绝缘态和莫特绝缘态很有可能有不一样的物理机制,例如理论研究者提出了激子密度波的物理图像[58].Imamoǧlu 课题组[43]设计和制备了MoSe2-hBN-MoSe2器件,两层MoSe2之间的转角小于1°,通过研究电荷在两层MoSe2之间的转移发现当上层或者下层MoSe2的填充因子为1 时,体系处于不可压缩态-莫特绝缘态.由于薄层hBN将两层MoSe2在空间上分开,MoSe2-hBN-MoSe2的莫尔周期势远小于TMDs 直接接触的转角体系.值得指出的是,双层TMD 同质结由于具有更高的轨道简并度,理论上可能存在拓扑非平庸物态[52,53,59],而双层TMD 异质结由于轨道简并度为1,一般认为只包含拓扑平庸物态(为简单起见,目前的讨论仅局限于K能谷).而实验上,虽然未在双层TMD同质结中观测到拓扑非平庸的现象,但是在MoTe2/WSe2中,通过施加极大的外加电场,使得MoTe2和WSe2的价带的能量互相接近,并发生杂化,实现了量子反常霍尔效应[51](见4.1 节).

3.2 广义维格纳晶体(generalized Wigner crystal)

与传统的强关联材料不同(例如铜基高温超导[56]),由于二维材料中屏蔽效应的减弱,莫尔超晶格中的近邻和次近邻库仑相互作用变得不可被忽略,从而导致广义维格纳晶体的形成[60,61],见图2(b)—(d).相比于二维自由电子气中维格纳晶体(要求Wigner-Seitz 半径rS≥ 31,正比于电子库仑相互作用和动能的比值)[62],莫尔周期势的存在使得广义维格纳晶体更加稳定.

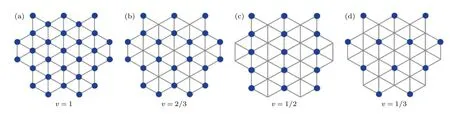
图2 转角TMDs 中的关联绝缘态的电荷分布示意图Fig.2.The schematic of the correlated states in twisted TMDs.

多个课题组[41,42,63]在转角半导体TMDs 观测到了丰富的广义维格纳晶体.Wang 课题组[42]利用3.1 节中讨论的光学技术研究了WSe2/WS2在填充因子远离1 的情形,在 1/3 和2/3 填充因子处发现了关联绝缘态,即广义的维格纳晶体(图2(b),(d)).在这些分数填充时,电荷排布形成了不同于莫尔超晶格平移对称性的周期性结构,例如,在1/3 和2/3 填充因子时,电荷分别形成新的三角晶格和蜂窝晶格.Mak 和Shan 课题组[41]设计了一种新颖的器件结构,将单层WSe2堆叠在转角WSe2/WS2之上,中间用薄层hBN 隔离.研究者利用单层TMDs 中的里德伯激子(2S 激子)作为“探针”,表征了2S 激子反射谱随莫尔超晶格中电荷浓度的依赖关系,发现了许多分数填充因子下的广义维格纳晶体,例如1/3,2/3,1/2,2/5,3/5 等,见图2.这些维格纳晶体也被近场微波阻抗测量所验证[63].同时,研究者进一步研究了WSe2/WS2的光学克尔效应,发现体系在1/2 填充因子时处于条纹态(stripe phase),打破了莫尔超晶格的旋转对称性[64],见图2(c).通过表征WSe2/WS2中磁化率随电荷浓度的依赖关系,发现在2/3 填充因子处由于广义维格纳晶体的形成使得反铁磁相互作用被极大地减弱[65].Wang 课题组[66]还进一步利用STM 直接表征了转角WSe2/WS2中电荷的空间分布随电荷浓度的依赖关系,直接观测到了广义维格纳晶体在1/3 填充因子处呈三角晶格,2/3 填充因子处呈蜂窝晶格,1/2 填充因子呈条纹状晶格.

4 转角半导体TMDs 中的电子态调控

4.1 电子关联性调控

通过调控电子关联性,即U/W,可以产生丰富的物理现象.例如,研究者通过计算发现当三角晶格中电子关联性逐渐减弱,填充因子为1 的基态将从120°非共线反铁磁,转变为非磁性绝缘态,最后变为费米液体金属态,其中非磁性绝缘态被认为是量子自旋液体的候选者[67−69].然而,传统强关联材料的电子关联性和材料本身锁定,对其调控往往需要通过极端的高压条件改变晶格常数来实现[70],实验上较为困难.而莫尔超晶格由于其构成材料的丰富性和优异的调控性能,为电子关联性的调控和新物态的发现创造了新的机遇.

4.1.1 金属-绝缘态相变

多个课题组在转角半导体TMDs 中实现了电子关联性驱动的金属-绝缘态相变[71,50,72].Mak 和Shan 课题组[50]在0°转角的MoTe2/WSe2中实现了对电子关联性的连续调节,发现了莫特绝缘态-金属态的连续相变.研究者巧妙地利用了 MoTe2/WSe2较大的晶格失配比(～8%),制备了高电荷浓度的莫特绝缘态(～5×1012cm–2),克服了TMDs和金属接触具有极大接触电阻的难题,为开展高质量的电学输运测量创造了条件.研究者利用外加电场减小MoTe2和WSe2价带之间的能量间隙,从而等效地增大能带宽度,发现莫特绝缘态连续地演变成了金属态.通过标度分析,发现不同电场下的电阻变温曲线“塌缩”至两条金属和绝缘态的曲线,并确定了量子临界点.同时,Dean 课题组[71]也在转角双层WSe2中,发现了电荷掺杂驱动的金属-绝缘态的相变,并发现电阻在相变点处表现为奇异金属(strange metal)—电阻随温度成线性变化.Mak 和Shan 课题组[72]还进一步制备了转角MoSe2/WS2,利用外加电场调控MoSe2/WS2能带宽度以及2 S 激子反射谱探测介电常数,发现了广义维格纳晶体绝缘态-金属态的连续相变.

4.1.2 拓扑非平庸的关联电子态

一般认为双层TMDs 同质结中的双轨道能带可以构造非平庸的拓扑态[52,53,59],而双层TMDs 异质结中的低能量电子态(单轨道)一般是拓扑平庸的.例如,双层MoTe2中价带顶位于K处(W的及S 的 px和 py轨道),具有巨大的自旋轨道耦合并且层间耦合较弱,具有来自上下两层的简并度(轨道简并度为2),进一步通过莫尔超晶格中位置依赖的层间耦合,可以构造出层赝自旋(layer-pseudospin)磁场势,从而具有拓扑非平庸物态[53].与双层MoTe2形成强烈对比的是,在双层WS2中,由于价带顶来自布里渊区中的Γ处(W 的和S 的 pz轨道),价带电子相互杂化从而层间退简并,形成了反键(antibonding)态(和高能量的键(bonding)态远远分开,轨道简并度为1),从而只具有拓扑平庸物态[73].虽然至今仍然没有双层TMDs 同质结中非平庸拓扑物态的实验报道,令人惊讶的是,Mak 和Shan 课题组[51]在60°转角的MoTe2/WSe2异质结中观测到了拓扑非平庸的关联电子态.相比于0°转角样品,在外加电场驱动下,60°转角的异质结中填充因子为1 的基态不仅从莫特绝缘态逐渐转变到金属态,在相变附近,还在零磁场下具有整数化的霍尔电导—量子反常霍尔效应(电导为e2/h,转变温度为2 K 左右).研究者还进一步在填充因子为2 处发现了量子自旋霍尔效应,观测到了接近整数化的电导(≈2e2/h,转变温度为2 K 左右)[74].并且,该体系中MoTe2的价带较平,提供了局域化空穴,而WSe2的价带能量色散较大,提供了巡游的空穴.研究者通过分别调控局域化空穴和巡游空穴的浓度,发现了重费米子的证据,实现了Kondo 晶格[75].

4.2 其他新型的调控方式

4.2.1 光学调控

Xu 课题组[76]设计和制备了转角WSe2/WS2并利用栅极电压对其进行电荷掺杂,通过共振光学激发产生层间激子,发现体系处于铁磁态.该铁磁态的机制被认为类似于RKKY[77],电荷“浸没”在层间激子中,并通过其实现了电子在不同晶格位之间自旋关联.

4.2.2 库仑屏蔽调控

Mak 和Shan 课题组[65]设计和制备了一种新型的器件结构,将薄层金属二维材料放置于转角WSe2/WS2之上,中间用薄层hBN 隔离,发现金属的库仑屏蔽效应可以使转角TMDs 中维格纳晶体绝缘态转变成金属态,并且原来的反铁磁相互作用被极大地抑制.

4.2.3 压力调控

Wang 课题组[78]发展了原位调控压力的技术,利用光纤头按压转角WSe2/WS2从而调制层间耦合,通过反射谱和荧光谱,发现了莫尔激子随着压力增大不断红移.

5 莫尔激子

与电子能带类似,激子在莫尔周期势下会形成多个莫尔能带,从而导致莫尔激子的出现.Mac-Donald 课题组[16]通过连续模型计算了转角TMDs异质结中的激子能带,研究了莫尔激子的反射谱随转角的依赖关系,并发现莫尔激子具有非平庸的拓扑性.Wang 课题组[79]和Tartakovskii 课题组[80]分别实验研究了转角WSe2/WS2和转角MoSe2/WS2,通过反射谱测量发现原本单一的激子反射峰在小角度转角TMDs 中演变为多个激子峰,即莫尔激子.Xu 课题组[81]和Li 课题组[82]也各自通过荧光谱测量在转角MoSe2/WSe2中观测到了莫尔激子的证据.进一步,Mak 和Shan 课题组[83]通过电场调控,在WSe2/WS2中观测到了层间激子和层内激子的强烈杂化效应.Louie 课题组[84]通过第一性原理计算,并考虑了晶格重构效应,指出转角WSe2/WS2中构成莫尔层内激子的电子和空穴分布在不同的莫尔晶格位上.Xu 课题组[85]和Liu 课题组[86]各自通过调控转角WSe2/MoSe2中的电荷浓度,发现了莫尔激子和电荷耦合形成的莫尔带电激子.Jin 课题组[87]利用光学泵浦产生层间激子,同时结合反射谱测量莫尔激子的能谱变化,寻找到了基于层间激子的玻色莫特绝缘态的证据.

6 展 望

莫尔超晶格领域在短短几年间得到了喷涌式的发展,未来也将充满丰富的可能性.首先,目前被深入探索的莫尔晶格体系主要集中于石墨烯和TMDs,相比于庞大的二维材料体系仍然十分稀少.探索基于其他二维材料的莫尔超晶格体系(例如,基于斜方晶体二维材料探索二维矩形或一维的莫尔超晶格中的强关联物理[88−90]),对于发现新物态和新物理将有着重要作用,这也有待理论和实验研究者的共同努力.其次,探索新型的莫尔超晶格调控手段也是一个重要的方向.例如,目前莫尔周期势主要取决于转角,但是器件制备完成之后转角难以调控.能否发展连续调控莫尔周期势的方法,例如压力[91]和应力调控[92],对于研究莫尔超晶格中的物态机理十分重要.同时,莫尔超晶格器件往往具有较为复杂的器件结构,极易出现“气泡”以及转角不均匀性等缺陷[49,93].如何克服上述困难从而进一步提高器件质量,将为发现新物态创造更多可能性.最后,当前已有一些室温条件下基于转角半导体TMDs 的光电器件的研究[94,95],持续地探索莫尔超晶格在实际应用中的可能性将对于保持整个领域的活力十分重要.