基于FL-XGBoost算法的砂泥岩识别方法——以胜利油田牛庄地区为例

彭 英，李克文，朱应科，徐志峰，杨澎涛，孙秀玲

（1.中国石化胜利油田分公司物探研究院，山东东营257000；2.中国石油大学（华东）计算机科学与技术学院，山东青岛266580；3.山东胜软科技股份有限公司，山东东营257000）

岩性识别对石油勘探开发具有重要意义，已成为众多学者关注的焦点。砂泥岩识别是储层预测工作中非常重要的环节［1］，也是诸多研究的基础，其所需的测井资料通常由专家按经验解释完成，因此识别结果存在一定的主观性。在常规的砂泥岩识别方法中［2-6］，地震反演作为砂体预测的常规技术已得到广泛应用，但不论是叠后反演还是叠前反演，均受限于地震的纵向分辨率，井间预测结果分辨率较低、可靠性较弱，准确率有待进一步提高。对于岩性信息的获取多依靠实地岩心取样、交会图和聚类分析［7］等传统方法和数理统计方法，但这些方法仍存在人力和时间成本较高等局限，因此有必要提出更可靠、稳定的学习算法以解决地质应用中砂泥岩自动识别分类的问题。

近年来，随着计算机硬件性能的高速提升以及大数据技术的不断发展，对石油工业的发展产生了巨大的推动作用［8］。因此，将迅速发展的大数据技术与测井曲线相结合识别砂泥岩，已成为目前储层研究砂泥岩识别的重要手段［9-14］。机器学习算法从井点出发，充分挖掘地震属性与测井岩性敏感曲线之间的数据关系，最大限度地发挥地震属性的利用价值，其预测结果的纵向分辨率高于确定性反演，井间可靠性优于地质统计学反演。随机森林算法［15-17］的训练速度快、准确率较高，能够有效地运行于大型数据集，且引入随机性，不易过拟合；该算法对于不平衡的数据集可以平衡误差，但对于小型数据或低维数据（测井数据），则难以产生较好的分类，易出现很多相似的决策树，导致真实的预测结果被掩盖。深度神经网络算法［18-22］可以较好地解决非线性问题，进而实现面向相关专业领域的迁移学习，这是建立在充足训练数据量的基础之上，但若在岩性识别任务的训练过程中，面对较为稀少的测井数据，神经网络在推理过程中无法提取足够的测井特征，易导致过拟合问题［23］，使得模型无法获得较高的准确率。XGBoost 是一种基于迭代决策树模型的集成学习算法［24-26］，是基于利用一阶导数相关信息的迭代决策树（Gradient Boosting Decision Tree，简称GBDT）的改进算法，在很大程度上提高了模型的训练速度和预测的准确度。对于深度学习算法而言，XGBoost 算法只适用于处理结构化的特征数据，而直接对测井、录井曲线等数据进行处理则较为困难，且XGBoost算法的参数过多，调参复杂。

由以上分析可以得出，诸如随机森林、深度神经网络等机器学习算法可以较好的解决相关地质问题，已经获得了显著的效果，为提升地质工作效率提供了新的思路和方法，然而在砂泥岩识别领域仍存在关键技术难点：①样本集的选取以及预处理对于机器学习算法的性能具有较大影响。②砂泥岩岩性数据复杂多样，根据测井参数与岩性的分析，选取合适的测井曲线参数是影响砂泥岩识别准确性的关键之一。因此，需基于特定样本数据设计相关人工智能算法与超参数调优策略，充分发挥智能算法的优势，以满足砂泥岩识别准确性的需求。

为此，笔者以测井和录井资料为基础，考虑砂泥岩识别的关键技术难点，对测井参数进行敏感性分析，以明确影响因素；通过多项预处理操作构建完整的训练数据集，根据测井标签稀疏性的特点，将Focal Loss 函数引入XGBoost 算法（FL-XGBoost算法），对胜利油田牛庄地区构建砂泥岩识别模型；并将随机森林、深度神经网络算法的训练结果作为对照，以最终砂泥岩识别分类结果的准确率作为评价标准，验证FL-XGBoost算法应用于测井砂泥岩识别的可行性；最后通过5 种公开分类数据集设计对比实验，验证FL-XGBoost算法在识别分类领域上的强泛化能力。研究成果可以为FL-XGBoost 算法对砂泥岩识别的可行性提供理论依据，为传统的测井岩性识别提供新的思路。

1 相关理论

GBDT 算法是一个树结构（可以是二叉树或非二叉树）［27］，由多棵决策树组成，以所有决策树的结论累加起来作为最终答案，具体原理为：每个非叶子节点表示一个特征属性的测试，每个分支代表这个特征属性在某个值域的输出，而每个叶子节点存放一个类别，迭代决策的过程是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果［27］。GBDT 算法的思路是不断地添加决策树，进行特征分裂以生长一棵决策树，且每次添加一个决策树，为学习一个新函数，进而拟合上次预测的残差。当训练完成得到k棵决策树，则要预测一个样本的分数，其实就是根据这个样本的特征，在每棵决策树中落到对应的一个叶子节点，每个叶子节点即对应一个分数，最后只需将每棵决策树对应的分数相加即为该样本的预测值。

XGBoost 算法是基于二阶泰勒展开式将损失函数展开，并且将正则项置于目标函数之外，这降低了模型的复杂度，更易于获得最优解，通过控制目标函数的不断下降，使得模型能够更好地收敛，有效避免过拟合，从而提高了预测准确率。该算法在训练前对数据进行预处理，将其结果保存，在后面的迭代中可以重复使用，从而降低计算复杂度，实现并行化，提高整体计算效率。

2 基于FL-XGBoost 算法的砂泥岩识别模型构建

基于GBDT与XGBoost算法，将不平衡样本分类思想引入训练损失函数，构建基于FL-XGBoost算法的砂泥岩识别模型。结合砂泥岩识别存在的关键技术难点，首先对测井参数进行敏感性分析，以明确影响因素，通过多项预处理操作构建完整的训练数据集并将其输送至FL-XGBoost模型中进行训练，迭代计算FL损失并判断是否继续收敛，期间进行超参数调优，最终获得训练完备的砂泥岩识别模型。基于FL-XGBoost算法的砂泥岩识别流程如图1所示。

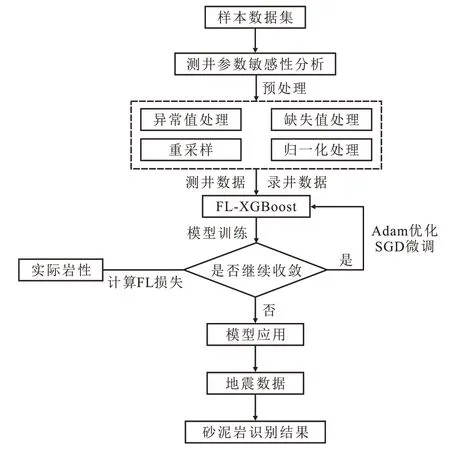
图1 基于FL-XGBoost算法的砂泥岩识别流程Fig.1 Flow chart of sandstone and mudstone identification based on FL-XGBoost algorithm

Focal Loss 是LIN 等于2017 年专门为解决不平衡分类问题提出的损失函数［28］。其从2个方面解决数据类别不平衡的问题：①损失函数更加倾向于关注少数类样本。②避免易分类样本主导模型训练过程而导致的性能降低。相对于庞大的地震数据体，测井与录井标签数据存在稀疏性，基于机器学习算法的砂泥岩识别可视为非平衡样本训练问题。

FL-XGBoost算法的思路与集成学习中的GBDT算法的类似。FL-XGBoost 算法训练时每一次迭代会增加一棵决策树来拟合上一次迭代过程中的真实值与预测值之间的FL 残差，进而逐渐逼近真实值，其训练过程中的目标函数为：

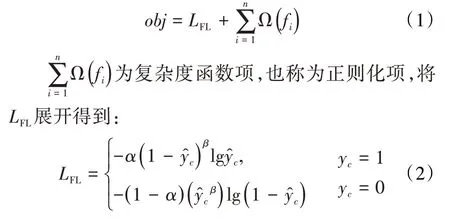
在（2）式中，通过引入系数α来调整测井标签中不同参数在损失函数中的权重，引入聚焦稀疏系数β来调整易分类样本和难分类样本的损失权重。

将Ω(fi)展开得到：

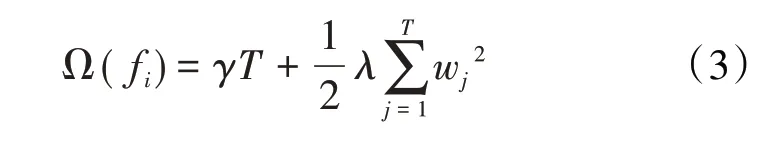
新生成的决策树需拟合上一迭代预测的残差，即第t次迭代目标函数，其砂泥岩识别结果可以表示为：

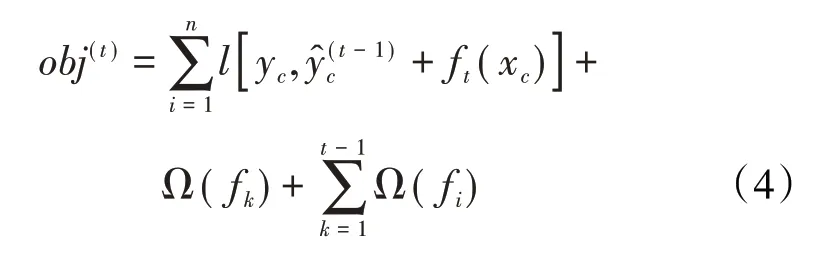
将损失函数使用泰勒二阶展开，引入正则项并去除常数项后得到：

将（5）式中表示的所有训练样本按照叶子节点进行分组得到：

FL-XGBoost 算法中经过k次迭代后，形成的决策树模型对第c个样本的输出结果为：

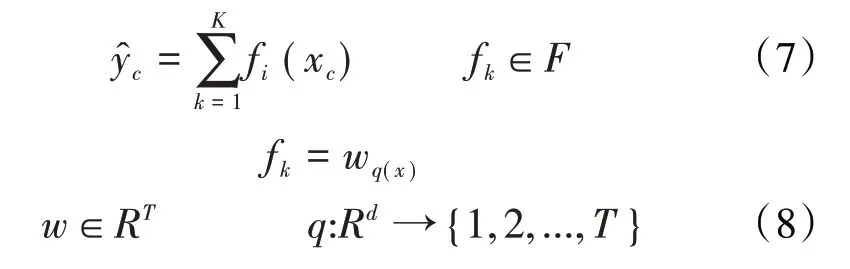
3 应用实例分析

3.1 研究区概况

牛庄洼陷为济阳坳陷东营凹陷中南部的次级洼陷，为渤海湾盆地油气最丰富的地区之一。其南北两侧均受断层控制，构造活动较为频繁，沉积岩性主要为深灰色的厚层泥岩、灰质砂岩和泥质粉砂岩等。牛庄洼陷发育多种类型的油气藏，对其地层岩性的准确识别可为后期的油气预测奠定基础。

3.2 数据获取及预处理

本次研究数据来源于牛庄洼陷220口井的测井及录井数据，其中200 口井的测井曲线为las 文件格式，20 口井的测井曲线为文本文档，采样间隔均为0.125 m。目标任务为完成纯泥岩、砂岩、其他泥岩（除纯泥岩之外的泥岩）、其他岩层（除纯泥岩、砂岩、其他泥岩三者之外的岩层）4 类岩性的识别。利用实际采集到的测井和录井数据，检查标签数据，建立样本库，并对样本数据进行预处理，包括：①异常值处理。根据业务专家制定的不同特征的合理取值范围，对数据中的特征值设置阈值并进行过滤，对超过阈值的不合理值依据临近数据或单井平均数据进行修正。②缺失值处理。对于测井曲线中的缺失数据，利用贝叶斯估计插补缺失值。③重采样。将测井数据采样间隔为0.1 m 的井应用插值进行重采样，采样间隔为0.125 m；对标签数据进行上采样，以保证标签类别均衡。④数据归一化。在机器学习领域中，不同特征向量往往具有不同的量纲和单位，这样会影响数据分析的结果。为了消除特征向量的量纲影响，需进行数据标准化处理，以解决数据指标之间的可比性。而原始数据经过数据归一化处理后，各指标处于同一数量级，适合进行综合对比评价（图2）。

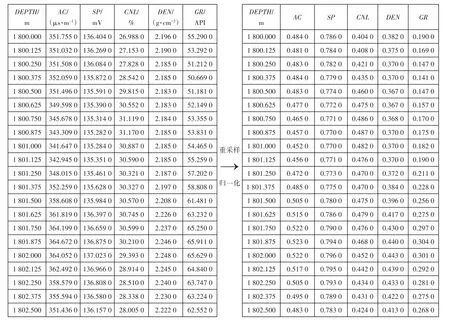
图2 数据重采样和归一化示例Fig.2 Diagram of data resampling and normalization

最终将整个数据划分为训练集、测试集和验证集。训练集和测试集数据是利用岩屑录井资料确定，为避免岩屑录井资料的错误，在岩屑录井图上，显示4条岩性曲线，即自然电位曲线（SP）、自然伽马曲线（GR）、井径曲线（CAL）和声波时差曲线（AC）。业务专家现场对岩性分类进行审定，去除不可靠的岩性分类，最终完成纯泥岩、砂岩、其他泥岩、其他岩层4 类样本的标定工作，按点构建1 048 575 条样本数据。4 个点构建1 个深度段，按深度段构建28 619条样本数据（表1）。

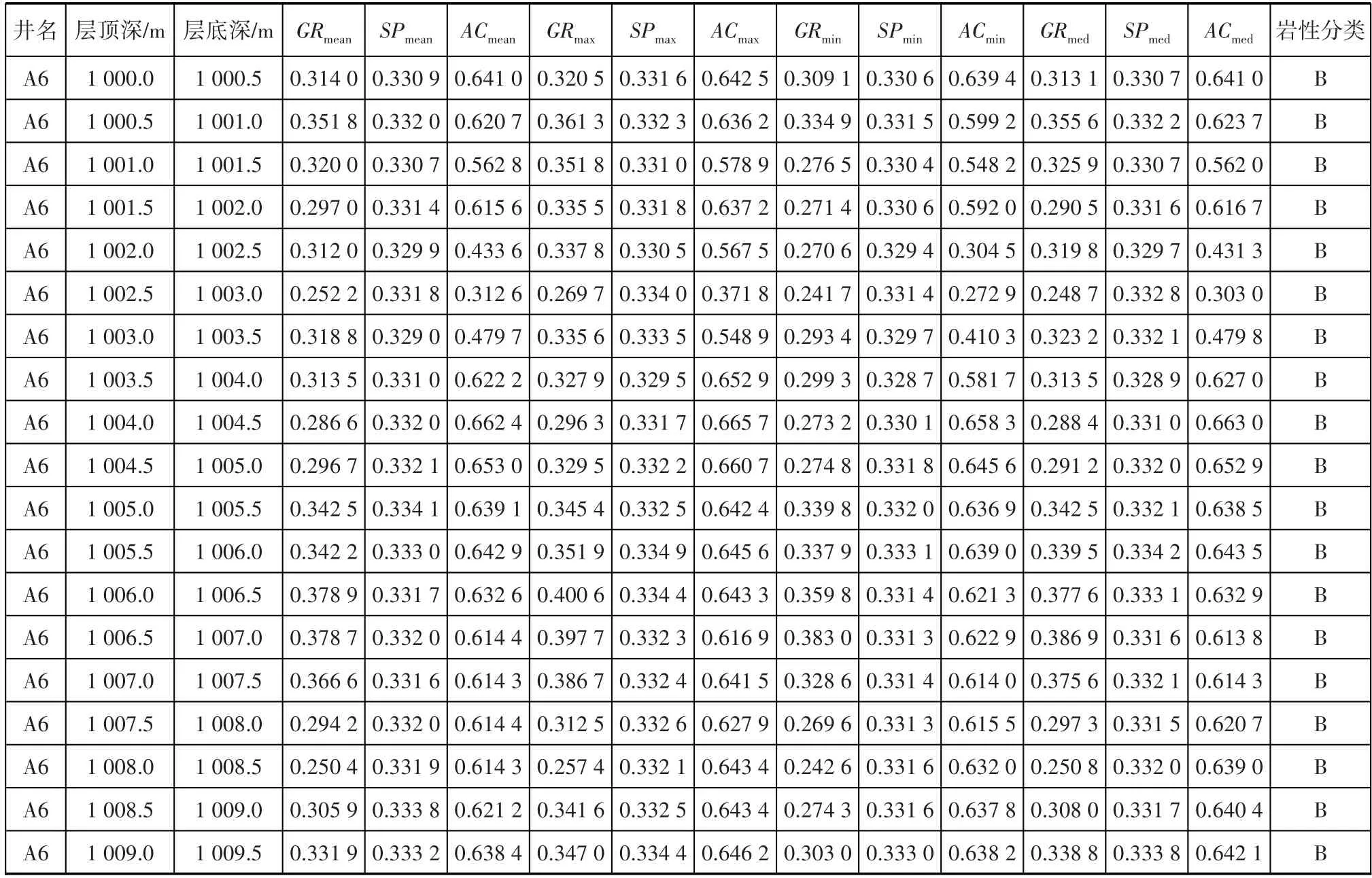
表1 样本数据的样式Table 1 Sample data style

3.3 特征参数提取

针对测井曲线数据进行多维度表征，测井曲线按点构建以及按0.5 m 每段提取特征参数。牛庄洼陷主要为砂泥岩沉积，且该区测井资料大多是2010年以前测得，9条基础测井曲线齐全，其他测井曲线较少，其中与岩性相关的测井曲线有GR，SP，AC和CAL曲线，而CAL曲线受钻井和裂缝的影响较大，因此选取AC，GR和SP这3条测井曲线作为岩性识别的基础数据。录井资料的采样间隔为0.5 m，测井资料的采样间隔为0.125 m，为了匹配录井数据，将测井资料按照0.5 m 进行特征参数提取，特征参数有最大值、最小值、平均值、标准差、中位数、累加值、数值排序的百分比；经过特征参数与岩性参数交汇分析，优选最大值、最小值、中位数、平均值作为测井曲线特征，分别提取每条测井曲线同一时窗内的最大值、最小值、中位数和平均值作为曲线的特征。

将处理后的特征数据与录井数据按深度进行匹配构建样本数据，并将样本数据划分为训练集和验证集，其中训练集样本占样本总数的80%，验证集样本占样本总数的20%。标签共包含4 类，分别为纯泥岩、砂岩、其他泥岩和其他岩层。

3.4 砂泥岩识别结果对比

分别使用FL-XGBoost 和XGBoost、随机森林、深度神经网络算法学习胜利油田牛庄洼陷的砂泥岩样本数据，并进行超参数设置、模型性能以及应用效果的对比分析。

3.4.1 FL-XGBoost算法

为契合砂泥岩识别，改进目标函数的计算方式，进一步提高模型的精确度，并将目标函数的优化问题转化为求二次函数的最小值问题，利用损失函数的二阶导数信息训练决策树模型，同时将树复杂度作为正则化项加入到目标函数中，以提升模型的泛化能力。XGBoost 模型中有多个超参数，选出对模型影响较大的超参数作为网格搜索法遍历寻优的参数，其余超参数为默认值。在本次应用实例中，分别对以FL-XGBoost 算法和XGBoost 算法为基础设计的30棵决策树构建对比实验，即初始迭代30次。初始学习率采用0.01，控制每次迭代更新权重时的步长，设置每棵决策树的初始深度为3，最大值为20，并且设置早停轮数，防止模型过拟合。

由表2 可知模型学习率、决策树的最大深度和迭代产生决策树超参数的数量分别为10，10和5，将以上参数进行组合得到500条超参数组合。运用网格搜索法，遍历网格中的500条超参数组合，寻找最优超参数组合。随机取80%的训练集数据分批输入到XGBoost 模型中，用剩余20%的数据集对模型的精度进行评估。根据评估结果的精确度调整模型所用样本和超参数。利用训练好的XGBoost 模型，按照0.5 m 为一段对新井的测井数据进行预测，并输出预测结果，将预测结果与标签值进行比较，只统计纯泥岩和砂岩预测正确的数量，其他泥岩和其他岩性不参与统计。其中，预测准确率=（纯泥岩预测为泥岩+砂岩预测为砂岩）/（泥岩样本总数+砂岩样本总数）。

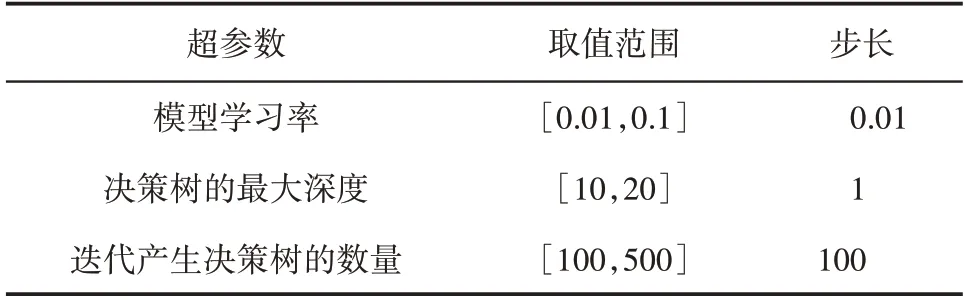
表2 FL-XGBoost算法参数设置Table 2 Parameter settings of FL-XGBoost algorithm

表3 显示在1 000 条超参数组合中具有代表性的组合与预测准确率，当决策树的最大深度为20、最优迭代次数为487 次，FL-XGBoost 模型的预测准确率达到最高值，为0.827，其在测试集下的推理速度为0.192 0 s，在迭代超过487 次以后，预测准确率出现持续的下降，推测模型出现过拟合现象。由此得到，当FL-XGBoost模型在更加侧重于测井资料方面训练，而非无关（负）样本训练时，模型的预测精度将会得到显著提高。

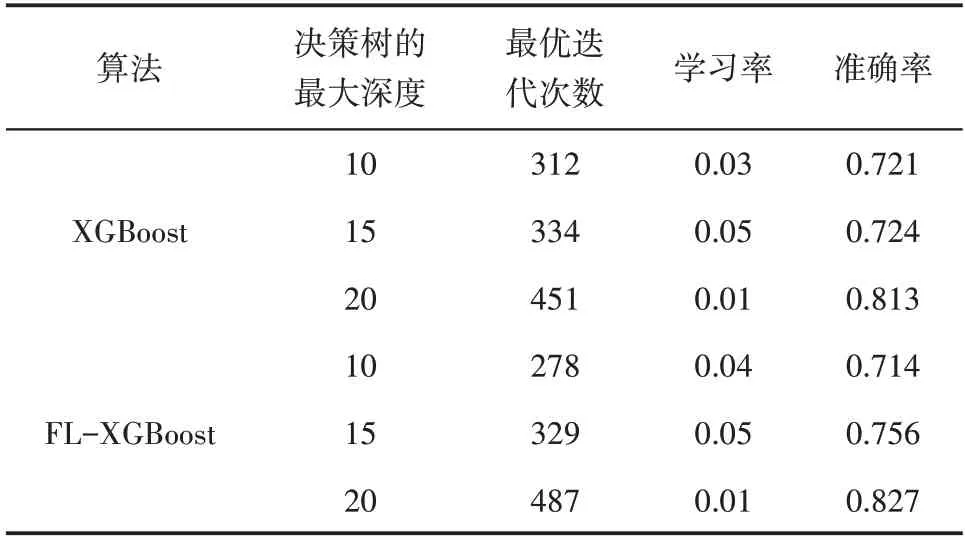
表3 XGBoost模型与FL-XGBoost模型迭代及识别结果Table 3 Iteration and identification results of XGBoost and FL-XGBoost models

3.4.2 随机森林算法

随机森林算法通过集成学习的方法集成多棵决策树，每一棵都是一个分类器，对于每一个输入样本，每棵决策树与分类结果是一一对应的，通过集成分类投票结果，将投票次数最多的类别指定为最终的输出。笔者将测井数据集作为输入，在基尼指数与交叉熵2 种标准下，对随机森林算法进行训练，并展示了迭代产生数、评判标准、决策树的最大深度等超参数对砂泥岩识别结果的影响（图3）。

由图3可知，随着迭代次数的增加，随机森林算法对砂泥岩的识别精度也在提高，但对于诸如测井数据的小样本数据，识别效果并不是最优的。在多参数设置最优的情况下，测试集的识别精度仅为74.13%，其在测试集下的推理速度为0.214 6 s。

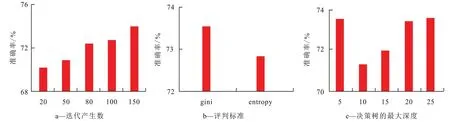
图3 随机森林算法结果分析Fig.3 Result analysis of random forest algorithm

3.4.3 深度神经网络算法

深度神经网络算法是机器学习的分支，是一种试图使用包含复杂结构或由多重非线性变换构成的多个处理层对数据进行高层抽象的算法。笔者将测井数据集作为输入，设计对应的深度神经网络模型，通过控制不同的隐含层数目与迭代次数进行训练，最终得到不同的砂泥岩识别结果（表4），在多参数设置最优的情况下，测试集的识别精度仅为0.745，其在测试集下的推理速度为1.453 1 s。

表4 深度神经网络模型及识别结果Table 4 Deep neural network model and identification results

深度神经网络算法虽然具有强大的非线性拟合能力，但这是建立在充足训练数据量基础之上的。面对较为稀少的测井数据量，该模型在推理过程中无法提取足够的测井特征，导致模型无法获得较高的准确率。

综合来看，采用FL-XGBoost算法的砂泥岩识别结果与采用随机森林、深度神经网络算法所得到的识别结果进行比较（图4），结果表明在使用交叉验证测试模型精度及相同训练数据下，使用FL-XGBoost 模型的训练速度最快，识别准确率有明显提升，同时计算复杂度更低，为砂泥岩的测井识别提供了新的思路。

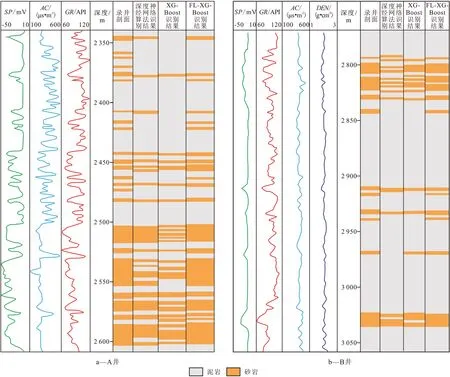
图4 不同算法的识别结果对比Fig.4 Comparison of identification effects of different algorithms

3.5 公共数据集及实验对比分析

在通用的分类识别问题中，业内常采用准确率、F1 值、AUC等作为评估指标，其计算所需的混淆矩阵如表5所示。

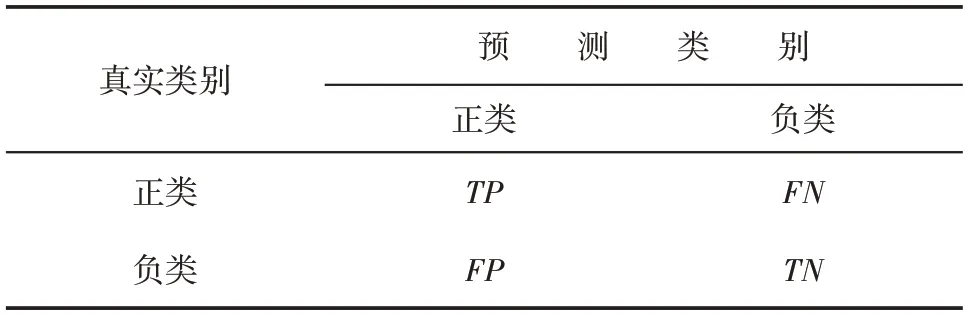
表5 混淆矩阵Table 5 Confusion matrix

利用混淆矩阵可计算相应的准确率、召回率、F1值和AUC等评估指标，其计算式如下：

KEEL 是一种集成海量标准分类数据集的综合库，为验证FL-XBoost 算法的有效性以及不同智能算法之间的性能差异，采用KEEL中的mushroom（蘑菇是否有毒的分类数据集）、magic（魔法射线望远镜数据集）、spambase（电子邮件分类数据集）、titanic（泰坦尼克轮船乘客的幸存分类数据集）、phoneme（声音分类数据集）等5 种公共数据集，其分别为特征数不同、样本量不同的代表性数据集。利用训练完备的随机森林、深度神经网络、XGBoost 和FLXGBoost算法分别对这5个数据集进行预测，并以准确率、F1 值和AUC作为评价指标，其数据集信息与预测结果如表6所示。

由表6 可知，FL-XGBoost 算法在5 种公开数据集中的预测结果均优于随机森林、深度神经网络和XGBoost算法，由于XGBoost算法中的正则化项可在一定程度上解决稀疏测井数据过拟合问题，不仅使用一阶导数，还推理二阶导数，使得损失函数更加精确。在此基础之上，FL-XGBoost 算法的损失函数相比于均方根误差、交叉熵等损失，Focal Loss 更加适用于难训练的样本，如测井曲线、录井数据等。因此，FL-XGBoost 算法的预测准确率相对于随机森林、深度神经网络、XGBoost 算法具有明显提升，具备更好的泛化能力。

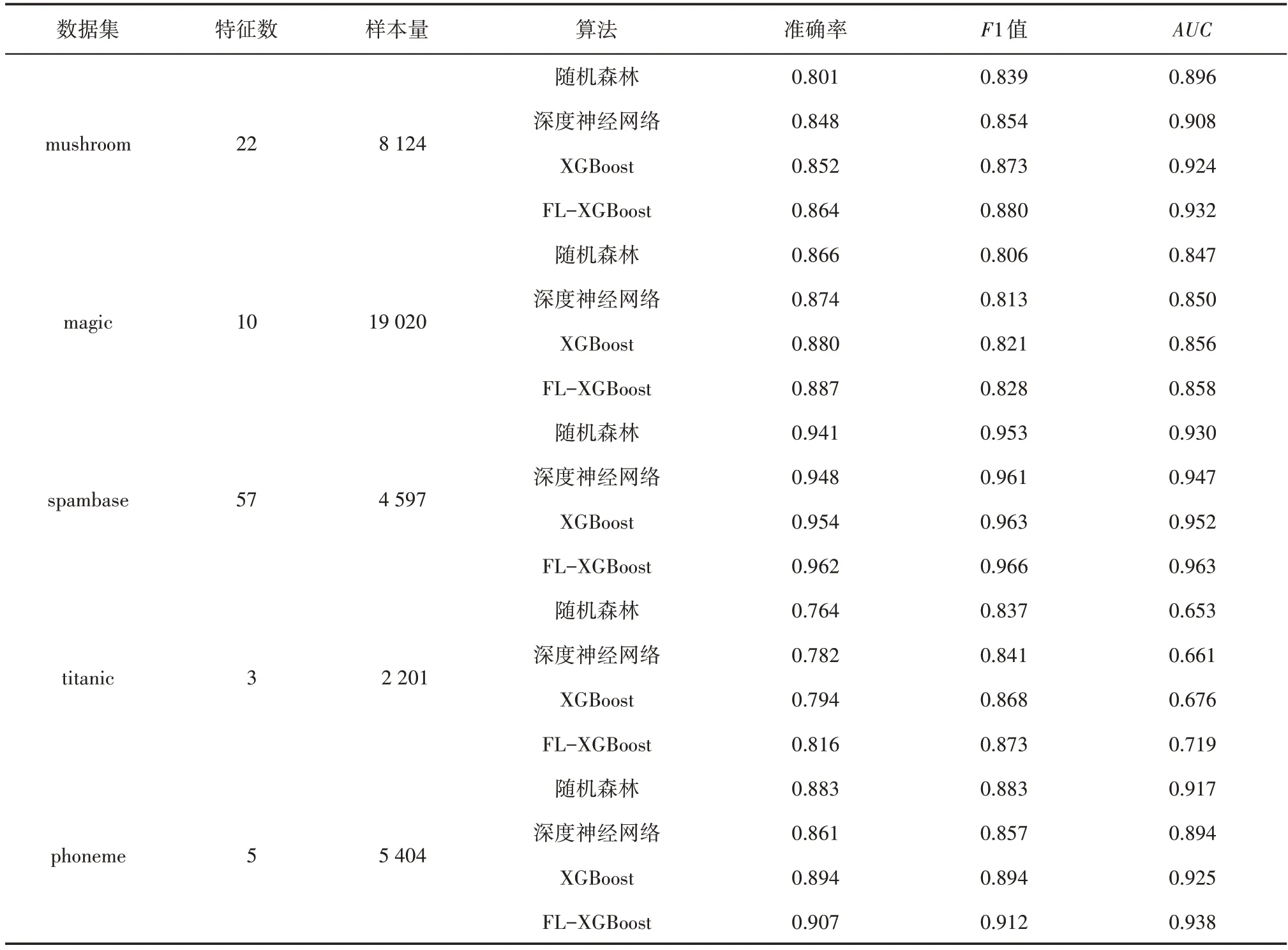
表6 5种公共数据集及预测结果Table 6 Five public datasets and prediction results

4 结论

以测井、录井资料为基础，结合砂泥岩识别任务存在的关键技术难点，对测井参数进行敏感性分析，以选取适当的影响因素。通过多项预处理操作构建完整的训练数据集，根据测井标签稀疏性的特点，将Focal Loss 函数引入XGBoost 算法，并对胜利油田牛庄洼陷构建砂泥岩识别模型，相比于随机森林和深度神经网络算法，FL-XGBoost 算法可以解决常规测井砂泥岩识别过拟合和准确率较低的问题。

FL-XGBoost 算法应用于砂泥岩识别任务的准确率达到0.827，构建智能化工作流程，同时形成测井岩性识别样本库，具有一定的泛化能力，可以在砂岩油藏中推广应用。FL-XGBoost 算法在KEEL中5 种公开数据集的预测效果均优于随机森林、深度神经网络和XGBoost 算法，证明该算法的有效性与泛化性。

符号解释

AUC——数据集中任取一个正样本和负样本，预测正例排在负例前面的概率，%；

c——地震道的道数，个；

f——F中的某棵决策树，棵；

fi——F中的第i棵决策树，棵；

fk——F中的第k棵决策树，棵；

ft——F中的第t棵决策树，棵；

F——特征空间；

F1——准确率与召回率的调和平均值，%；

FN——错误的负例，即错误的将样本中的正例识别为负例，%；

FP——错误的正例，即错误的将样本中的负例识别为正例，%；

gi——损失函数的一阶导数；

hi——损失函数的二阶导数；

i——当前决策树的棵树，棵；

j——当前的叶子节点，个；

k——当前的迭代次数，次；

K——总的迭代次数，次；

l——损失函数；

LFL——Focal Loss误差项，%，

n——FL-XGBoost算法的决策树数量，棵；

N——负样本，%；

NN——负样本（多数类）总数，%；

NP——正样本（少数类）总数，%；

obj——目标函数；

P——正样本，%；

Pre——准确率，%；

Pc——正样本的类别，无单位；

q——表示样本xc被预测后落入在对应节点上的概率，%；

ranki——正样本的置信度排序，%；

R——每个节点的分值集合；

Rd——每个节点的集合；

Rec——召回率，%；

t——当前迭代次数，次；

T——叶子节点的总个数，个；

TN——被预测为负类的负样本，%；

TP——被预测为正类的正样本，%；

w——叶子节点的分值，%；

wj——第j个叶子节点的分值，%；

wq——第q个叶子节点的分值，%；

xc——多地震道训练数据，个；

yc——与xc对应的测井和录井曲线标签数据；%；

——训练数据xc经所有预测后得到的估计值，%；

α——系数，%；

β——聚焦稀疏系数，%；

γ——可以控制叶子节点的个数，个；

λ——分数控制系数，可以控制叶子节点的分数不会过大，防止过拟合，%；

Ω（fi）——决策树的正则化项。