用数学打造完美 “发现生活中的黄金比”教学设计

◇崔慧慧（江苏：盐城市盐渎实验学校）

【教学目标】

让学生初步了解“黄金比”，感受“黄金比”带来的美；

让学生运用“黄金比”解决简单实际问题，进一步掌握比的知识，增强解决问题的策略意识；

让学生感受到数学与人类生活的密切联系，以及对人类历史发展的作用，激发学生学习数学的热情，培养学生发现美、欣赏美、创造美的情趣。

【教学重难点】

认识“黄金比”，感受“黄金比”的神奇作用；

发现“黄金比”，运用“黄金比”。

【教学流程】

一、课前热身，激发兴趣

师：课前我们来玩一个神奇的数学魔术。请你任意写2个数，把这2个数相加得到第3个数，再把第2个数和第3个数相加，得到第4个数……直到你有了7个数。用第6个数比上第7个数，看比值是多少？可以用计算器计算。大家在这里可以暂停一下。

学生操作计算。

师：我猜你们结果应该是比0.6多一点，我猜对了吗？老师是怎么未卜先知的呢？别急，学完这节课，你就都知道了。

二、推荐阅读，发现数学美

师：你们爱阅读吗？我也爱读书。我给大家推荐一套最近正在读的科幻小说——《银河帝国》。我可以为大家朗读其中的一段吗？

半空中，出现了婉达前所未见的种种符号，包括字母、数字、箭头和图案。

“美丽吗？”雨果问。

“嗯，美丽，不过我不喜欢那个部分，我想它错了。”她指向左方一个色彩缤纷的方程式。

“错了？你为什么说它错了？”雨果皱着眉头问。

“因为它不……美丽，换成我就不会这么做。”

（以上摘录自《银河帝国》第5册第321页。）

师：这一段文字给了我深深的震撼。婉达为什么觉得方程式不对？看来数学和美之间有着紧密的联系。

三、直观展示，发现问题

师：让我们欣赏生活中的美。可爱的狐狸、草叶上的一只瓢虫、阳光女孩、赏心悦目的盆栽。这些照片美吗？

师：比较一下，这里还有3张照片，你觉得哪一张最美？中间这幅图为什么最美呢？因为这里有黄金比。你们知道什么是黄金比吗？

师：老师在小鸟的位置添上辅助线段，标上字母。这条线把整个画面的长度一分为二，较长部分AC与整体AB的比值等于较短部分BC与较长部分AC的比值，它们的比值约为0.618。这个比被公认为最能引起美感的比，因此被称为“黄金比”。这节课我们就来认识黄金比。关于黄金比的知识，在古希腊数学家欧几里得所著的《几何原本》第二卷命题11里能找到，你们有兴趣课后可以看一看。

四、“黄金比与黄金螺旋线”

师：英国诗人同时也是画家的威廉·布莱克创作过一首诗。

从一粒沙里，你能看出一个世界，

在一朵野花里，存在一座天堂，

把无限放在你的手掌上，

永恒在一刹那里收藏。

师：就让我们走进美丽的世界。看，螺旋芦荟、鹦鹉螺、海洋上空的气旋、浩瀚的星海、辽阔的宇宙。从植物、动物、气候、宇宙的照片中，你们都发现了什么形状？这种形状在数学上叫作斐波那契螺旋线。

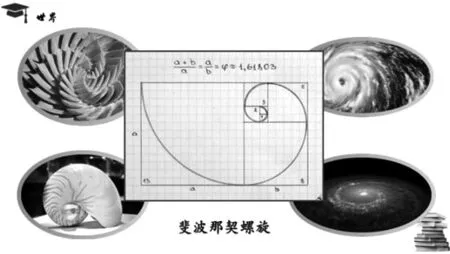
师：斐波那契对阿拉伯数字的推广做出了重要的贡献。他所著的《算盘书》广为人知，书中有这样的一列数：1，1，2，3，5，8，13，21，34……你们能看出它的奥秘吗？从第三个数开始，每个数都是和它相邻的前两个数的和。用前一个数比相邻的后一个数，算一算比值各是多少？它们的比值越来越接近0.618。所以这个数列叫作斐波那契数列，又叫作黄金数列。回到课前的魔术，如果你们所写的那一列数继续算下去，你觉得结果会越来越接近多少？这太神奇了！为什么会这样呢？老师借给大家一本书——《解读黄金比例》。你们可以在书里找到答案。

师：斐波那契螺旋线是怎么画的呢？我们看，这里正方形的边长分别是1，1，2，3，5，8……每一个正方形的边长数都符合斐波那契数列。再以正方形的边长为半径画圆弧，依次连接起来就画出了漂亮的斐波那契螺旋线，所以它又叫作黄金螺旋线。

五、自主探索，汇报交流

师：黄金比在我们的生活中有什么应用呢？老师提供一些素材，大家可以自主选择自己感兴趣的内容进行探究。下面的课堂交给你们，说说你们的发现。

（一）人体中的黄金比

预设：我汇报的是人体方面。我发现1号人物腿长和身高的比值是0.612，2号人物的腿长和身高的比值是0.561。1号的身材看起来更好，因为比值更接近0.618。

师：想知道他们是谁吗？1号是110米跨栏运动员刘翔，中国最伟大的田径运动员之一；2号是游泳运动员菲尔普斯，获得23枚奥运金牌，创纪录的第一人。芭蕾舞演员为什么跳舞的时候总是踮起脚尖呢？

师：老师这里有一把尺子，知道叫什么吗？黄金比例尺！它有什么作用呢？请看一段视频。请在视频里找出比。视频里的1∶1.618，比值是多少？小数部分完全相同。

（二）建筑中的黄金比

预设：我觉得右边的建筑方案更美观，因为它更符合黄金比。

师：我们一起欣赏多伦多西恩塔、上海东方明珠、巴黎埃菲尔铁塔。老师搜索关键字“黄金比”的时候，经常会出现雅典娜·帕台农神庙的照片，这些建筑大量运用了黄金比。有一位非常伟大的古典雕刻家菲迪亚斯（古希腊文Φειδίας），他雕刻了世界七大奇迹之一的宙斯巨像，也雕刻了帕台农神庙的雅典娜巨像。所以黄金比的符号Φ，就是他名字的首写字母。给大家推荐一本书——《φ的故事》。

师：所以建筑中也会用到黄金比。

（三）绘画中的黄金比

预设：我发现人物脸型也有黄金比。

师：这幅作品是世界名画《蒙娜丽莎》。我们从另一个角度来欣赏，人物脸型多处符合黄金比。

达·芬奇所著的《绘画论》一书开卷这样说：不懂数学的人，请不要读我的著作。所以绘画里也有黄金比。

（四）摄影中的黄金比

师：很多手机拍照时都有构图线这一功能，会出现横向和纵向的两条线。哪位同学愿意帮老师拍一张照片。你们想看一看拍摄效果吗？感谢这位优秀的小摄影师。

（五）植物中的黄金比

预设：我研究的是植物方面。我计算发现植物枝干夹角与圆周另一个角的比值大约是0.618。

师：在这个角度，植被的通风、采光效果是最好的。看，这是一朵雏菊，学名白晶菊。数一数，这朵雏菊有多少片花瓣？21这个数，在斐波那契数列里出现过。有资料说，雏菊的花瓣数都符合黄金数列。我也不知道真假，想验证一下吗？老师给大家带来了雏菊的种子，请大家精心培育，开花以后数一数。实践是检验真理的唯一标准。

（六）音乐中的黄金比

预设：我汇报的是音乐方面。这个乐谱一共89个小节，分成55小节和34小节。经过计算我发现，声音小和声音大的时长符合黄金比。声音小的这一段又分成34小节和21小节，经过计算也和黄金比有直接关系，34：55比值大约也是0.618。我觉得，音乐里，如果有对比性的两部分，它们的比是0.618的话，听起来会非常悦耳。

师：这首曲子叫作《为弦乐、打击乐与钢片琴而作的音乐》，我们一起欣赏。

师：所以黄金比如果应用到音乐上，也会让乐曲更加美妙。

六、辨识黄金矩形

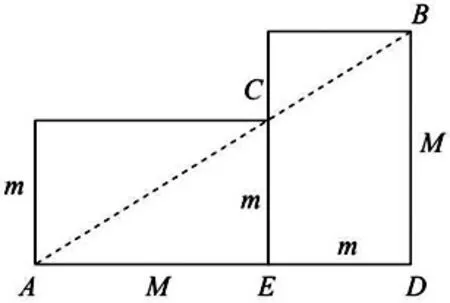
师：如何判断一个长方形符合黄金比呢？如果一个长方形的宽度和长度的比值是0.618，这样的长方形也叫黄金矩形。这几个长方形是黄金矩形吗？可以测量、计算，还可以借助黄金比例尺判断。其实还有非常便捷、准确、快速的方法。复制一个完全相同的，横过来放，只要一根直直的线条把对角线连起来。如果经过重合点，那就一定是黄金矩形。

师：大家回家以后用这个方法快速判断银行卡或者身份证，看它们的形状是不是黄金矩形。

七、应用黄金比

舞台上，你觉得演讲者站在什么位置比较好？

老师链接到国家地理中文网，大家自行欣赏。

这是投资理财的走势图，图中可以看到0.618。

八、拓展作业

师：大家可以自己做一个黄金比例尺。准备1厘米宽的木条四根，一根长13厘米，一根长21厘米，另外两根长34厘米，一端打孔，在距离13厘米处开另一个孔，这样组装起来就是一个黄金比例尺。发现没有，13、21、34都符合斐波那契数列。

师：这节课有收获吗？