如何让学生理解“余数要比除数小”

潘璐洁

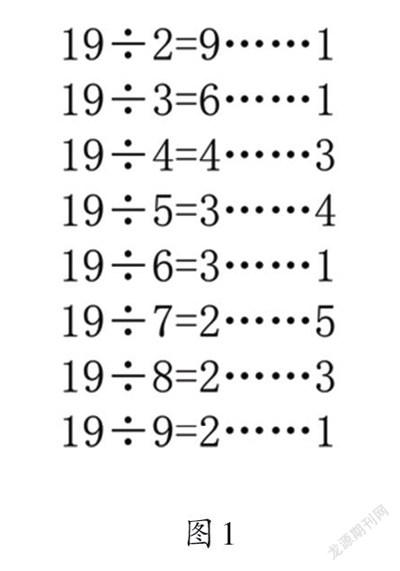
理解“余数要比除数小”是有余数除法的教学的重难点。可以采用以下教学过程帮助学生理解。

一、多元表征，促进理解

1.摆一摆，探一探

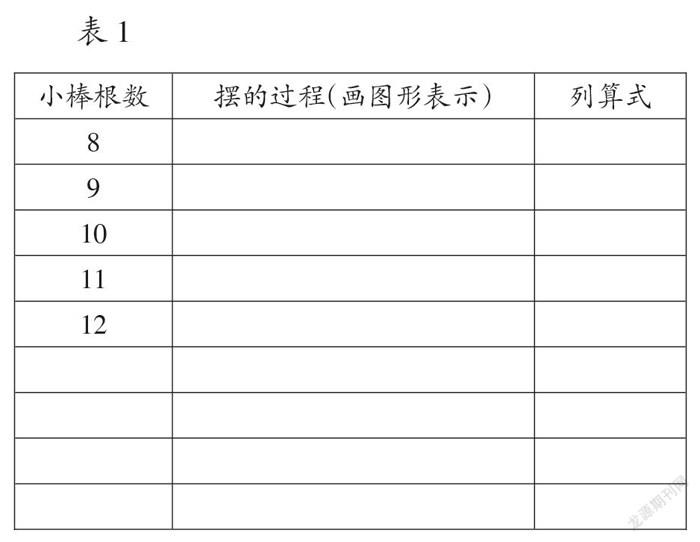
教师出示一个正方形，并引导：“摆这样的正方形要4根小棒，那么8根小棒可以摆几个这样独立的正方形？怎么列式？”“如果是9根小棒呢？10根、11根、12根……呢？”请学生同桌合作完成表1学习单。

2.想一想，说一说

教师进一步引导：“如果是13、14、15、16根小棒摆正方形，结果会怎么样？现在不摆小棒，你能直接写出算式吗？”学生汇报，教师补充表格。

二、引导观察，发现规律

1.发现余数周期性的出现

教师提问：“这组算式有什么规律？”“算式中的余数是怎么变化的？”学生讨论后发现余数是1、2、3、0（无）重复出现。

2.发现余数和除数的关系

教师提问：“想一想，如果用小棒摆五边形，可能会剩几根小棒？”并与学生交流：“摆五边形除数就是5，剩下的几根小棒其实就是余数，这时余数有怎样的规律？”

教师追问：“同样根数的小棒，摆正方形和五边形，剩下的小棒根数却不同，剩下几根小棒由谁决定？”

教师引导学生通过摆图形的过程，理解算式中的除数与余数的关系。

教师进一步追问：“如果用同样根数的小棒摆六边形，余数又会出现什么情况？”

教师小结：从摆正方形、五边形和六边形等图形的活动中，可以发现余数总比除数小。

三、巧用变式，深化认识

1.教师提供“19个点子图”学习单，让学生圈一圈，写一写，并用算式写出表示圈的过程与结果。学生独立完成后，教师用课件呈现8幅图与相应的算式。

2.教师提问：“仔细观察8个算式（如图1），你发现了什么？”引导学生进一步体会不管除数怎么变，余数都比除数小。

3.聚焦19÷2，19÷3，19÷6，19÷9這四个算式，教师提问：“这4个算式现在的余数都是1，也就是都余下了1个小圆点，它们分别再添几个小圆点就可以再圈一组？”引导学生思考：为什么都剩下一个小圆点，再圈出一组所添加的小圆点数量却不同？学生讨论后发现这是因为每组算式中除数不同，也就是每组中所含的小圆点数量不同。

上述活动中，学生经历了操作、观察、想象、比较、归纳等过程，能较好地理解余数要比除数小的原因。这为他们后续探究数学规律、解决数学问题打下了一定的基础。