基于地理探测器和GIS的压砂地砾石空间异质性及其影响因素分析

阮晓晗，白一茹，王幼奇，高小龙

（1.宁夏大学地理科学与规划学院，银川 750021；2.宁夏大学生态环境学院，银川 750021）

砾石是粒径≥2 mm 的矿物质颗粒，在土壤中广泛分布[1]。研究表明，砾石类型、粒径大小、砾石配比、形状、含量及其在土壤基质中的分布等能够显著影响土壤物理性质[2]、水分运动[3]、碳储存[4]及养分循环[5]，并且能制约地表结皮[6]及侵蚀[7]等一系列土壤过程。由于区位、气候和管理措施等不同，土体中砾石的空间分布在自然及人为作用的综合影响下存在明显的异质性，因此探究土体中砾石的空间分布特征能够为合理利用土地资源、明确灌溉定额及恢复区域生态环境提供理论依据。

近些年已有不少学者对土体中砾石的空间分布进行了研究，如Simanton 等[8]在美国亚利桑那州东南部的坡面研究发现，坡度梯度与地表岩石碎片含量显著相关（P＜0.01）。Poesen 等[9]对地中海半干旱丘陵和横断面的地表砾石进行了研究，发现砾石粒径大小和覆盖的空间变化主要受丘陵坡度梯度控制，同时坡向与坡位等也会显著影响砾石的空间分布（P＜0.05）。Govers 等[10]在西班牙东南部半干旱丘陵地区研究表明，土壤表面覆盖的砾石量不仅与坡度梯度有关，同时与曲率线性相关。朱元骏等[11]在黄土高原水蚀风蚀交错带研究了坡面表土砾石覆盖度和粒径分布特征，发现坡面砾石分布是侵蚀与坡度因素叠加作用的结果。冯雪瑾等[12]测定了太行山南麓地区不同坡位、不同土层深度的砾石含量及砾石粒径的分布特征，结果表明不同粒径砾石体积分数均呈现从坡顶到坡脚逐渐减小的趋势。Nyssen 等[13]的研究表明，耕地中砾石的空间分布受地形地貌条件、水文过程及人为作用共同影响。综上可知，在不同区域和尺度条件下砾石分布均存在明显空间异质性而主要影响因素有所不同，当前研究大多基于不同区域自然因素主导的砾石空间异质性研究，针对人为影响较大的土体含砾石区域研究较少，而压砂地等人为形成的特殊砾石-土壤聚集体中砾石的空间异质性及其影响因素研究相对缺乏。

压砂地是我国西北地区充分利用当地砾石资源，应对干旱气候的一种典型耕作模式[14]，其表面覆盖的砾石能够有效促进土壤水分入渗、增温保墒[15]。然而随着种植年限增加，压砂地的砾石与土壤层混合、连通，导致其土壤理化性质[16]、保水保墒功能变差[17]，干燥化程度加剧[16]。当前压砂地出现大量经长期种植后撂荒的现象，约有1/3退化严重，近年来宁夏各地区逐步开展压砂地有序退出及区域生态修复等工作，因此明确压砂地不同粒径砾石空间变异特征，并进一步分析其影响因素是研究压砂地退化机制的基础问题。为此本研究对压砂地不同粒径砾石进行统计分析，采用空间自相关和半方差函数的分析方法，从不同角度揭示研究区压砂地不同粒径砾石空间结构特征和分异规律，并通过地理探测器深入探讨种植年限、坡向和地表粗糙度等因子对不同粒径砾石空间分异的影响程度，选取影响因子较高的环境变量协同地理加权回归克里格法进行插值，获取了不同粒径砾石空间分布特征，以期为压砂地逐步退出、修复重建和分类施策等提供理论支撑。

1 材料与方法

1.1 研究区概况

研究区位于中卫市沙坡头区兴仁镇红沟（36°56′32″～36°57′45″N，105°22′22″～105°21′29″E），地处宁夏中部干旱带，属干旱半干旱气候，年平均温度6.9 ℃，≥10 ℃积温2 320 ℃，无霜期163 d 左右。多年平均降水量不足200 mm，年蒸发量2 390 mm左右，全年日照3 800 h 左右，光热资源十分丰富，昼夜温差大，土壤为灰钙土，是硒砂瓜主产区。覆盖砾石来自香山风化碎石，覆盖厚度为20 cm 左右，利用ArcGIS 10.6制作样点分布及高程图（图1）。

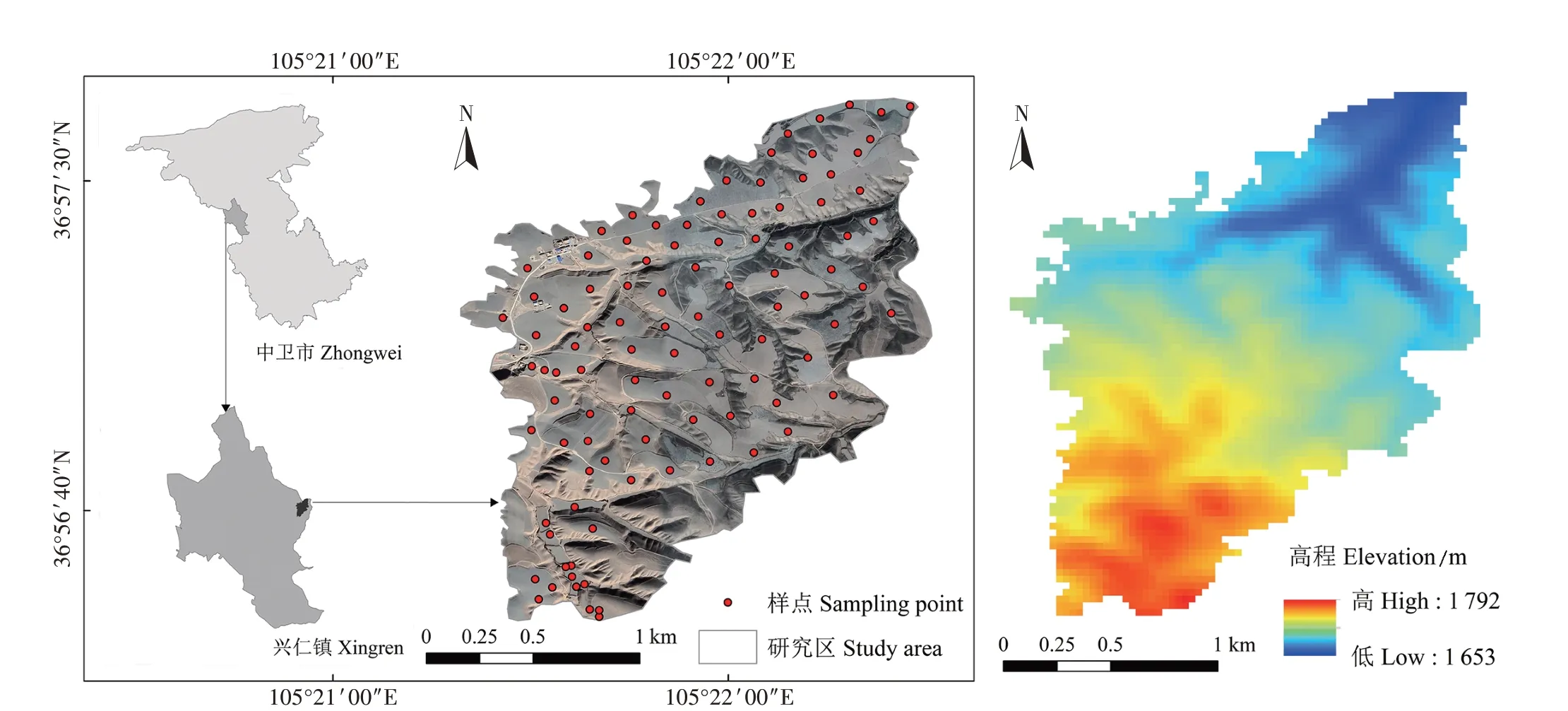
图1 研究区样点分布及高程Figure 1 Sampling point distribution and elevation of the study area

1.2 采样方法

2020 年9 月20 日至10 月5 日进行不同年限压砂地砾石分选。根据前期实地调研，明确了研究区范围内所有压砂地的种植年限，并将所有压砂地的种植年限划分为：2、5、10、20、30 a 和40 a。研究区总面积为2.54 km2，种植2、5、10、20、30 a 和40 a 的压砂地面积占比分别为10.75%、30.42%、32.37%、14.69%、5.92%和5.85%。在研究区压砂地集中分布区域根据各年限压砂地所占面积比，同时结合网格法均匀布点，样点数分别为11、31、33、15、6 和6，共计102 个。在每一个样点内选取50 cm×50 cm 范围内砾石覆盖层全部砂石，风干后用50、31.5、25、16、10、5、2 mm 筛子逐层过筛，选取不同粒径的砾石测定质量并记录，压砂地砾石粒径配比情况见表1。

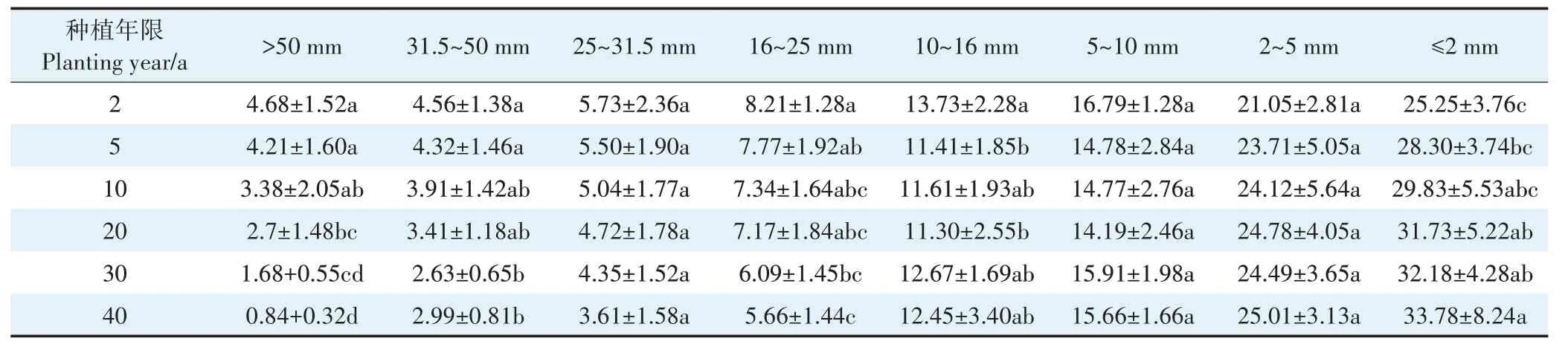
表1 压砂地不同粒径砾石配比（%）Table 1 Proportion of gravel with different particle sizes in gravel-sand mulched fields（%）

1.3 影响因子采集与分类

砾石空间分布受自然因素与人文因素共同影响，有研究表明土体中砾石的空间分布与地形因子之间存在紧密联系[8-10]，地形对土体内部砾石空间变异的影响不容忽视，这些地形因子能够通过DEM 获取[18]。本研究以研究区DEM 影像为基础，提取坡度、坡向、地表粗糙度、地表起伏度、剖面曲率及平面曲率6 种地形因子，并通过对研究区的前期调查获取压砂地种植年限数据，其中DEM 数据为30 m 的ASTER GDEM数据，来源于地理空间数据云网站。为充分考虑多因子对砾石空间分布的影响，本文选取自然因素和人文因素共7 个影响因子，并利用自然断点法，对数值型驱动因子进行等级划分。

1.4 统计分析方法

1.4.1 空间自相关分析

空间自相关是指地理对象的某一属性值在相邻空间位置处取值之间的相互关系，是对该属性空间聚集或分散程度的度量[19]。空间自相关现象广泛存在于地理空间数据中，因此，进行空间自相关分析对深入理解地理对象的空间分布特征具有重要意义。Moran′sI指数在地理对象的空间自相关性研究中具有广泛应用，其不仅能在总体水平上对空间自相关现象做出评价，而且能够对地理属性值的聚集和离散程度作进一步的区域可视化。本研究中全局空间自相关采用全局Moran′sI指数描述：

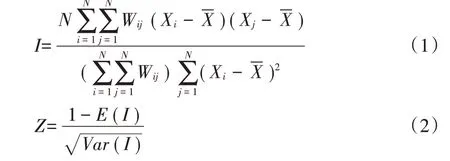
式中：N为采样点总数；Wij为空间权重；Xi和Xj分别为i处和j处的砾石含量；为砾石含量均值；Z为标准化统计量值；E（I）为观测变量自相关性的期望值；Var（I）为方差。Moran′sI指数的取值范围为[-1，1]，I＞0 代表属性值呈现空间正相关，趋于空间聚集；I＜0代表属性值呈现空间负相关，趋于空间分散；I=0代表属性值趋于空间随机分布。采用Z值进行显著性检验，当Z≥1.96或Z≤-1.96时，表示空间相关性显著（P＜0.05）。

1.4.2 空间变异性分析

采用地统计学分析压砂地不同粒径砾石占比的空间变异特征，其公式为：

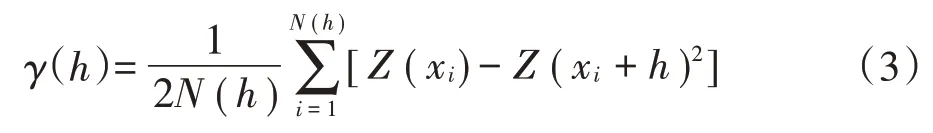
式中：γ（h）代表半方差函数值；N（h）代表相距为h的点对数；Z（xi）代表x=xi处变量Z的实测值；Z（xi+h）代表x=xi+h处变量Z的实测值。以滞后距h为横轴、半方差函数值为纵轴可以绘制半方差图。根据半方差图可以得到块金值（C0）、基台值（C0+C）、变程（A）三个重要特征值。C0表示随机部分引起的空间变异性；C0+C表示变量的最大变异程度；A表示变程，即变量自相关范围。通过公式C0/（C0+C）可以计算得到一个描述空间变量依赖性的重要指标，即空间异质比，根据Cambardella 等[20]的划分标准，C0/（C0+C）≤25%表示强的空间依赖性，25%＜C0/（C0+C）＜75%表示中等空间依赖性，C0/（C0+C）≥75%表示弱的空间依赖性。

1.4.3 地理探测器

地理探测器是探测空间分异并揭示某种地理属性与其解释因子之间关系的一种空间分析模型[21]，能够探测单因子对因变量空间分异的影响，并对其显著性进行统计学检验。本研究采用因子探测功能来分析各影响因子对压砂地土体中不同粒径砾石空间分异的影响。其计算公式[22]如下：

式中：Nh为子类型区h的单元数；L为变量的分层；N为全区的单元数；为不同粒径砾石占比在子类型h区的方差；σ2为不同粒径砾石占比在全区的方差。q值为某因子对不同粒径砾石空间分异的解释程度，其取值范围为[0，1]，值越大表示该因子对不同粒径砾石空间分异的解释力越强，反之则越弱。

1.4.4 地理加权回归克里格法

地理加权回归克里格法（GWRK）是通过对目标变量和辅助变量进行地理加权回归拟合（GWR），得到局部回归的残差项，然后使用普通克里格插值法（OK）对所得残差项进行插值[23]。GWR模型结构如下：

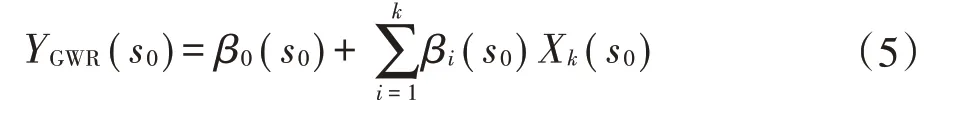
式中：YGWR（s0）为因变量Y在s0处的模拟值；β0（s0）为截距项；βi（s0）为第k个协变量的回归系数；Xk（s0）为第i个样点上第k个变量的测量值；s0为局部估计的系数，用加权最小二乘法求得，是空间位置的函数，其权重矩阵的估计采用高斯函数；k为自变量数。

GWRK 法是用OK 法对GWR 模型拟合后的残差进行插值，该方法是对GWR法的一种深入推广，并增加了GWR法拟合的趋势[24]，其表达式为：

式中：ε（s0）为GWR 模型在点s0处拟合后所得的残差，采用OK法进行插值。

1.4.5 精度评价

随机生成的80 个用于模型拟合的测试点参与所有分析过程，其余22 个测试点用于验证空间插值结果。用验证点估计值和实测值的平均相对误差（MRE）和均方根误差（RMSE）评价不同方法的预测准确性。

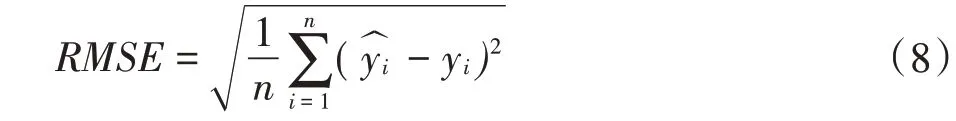
1.5 数据处理

利用SPSS 20.0 进行经典统计分析，在GS+9.0 软件中完成半方差函数分析，运用GeoDa 1.16软件进行全局空间自相关分析，在GeoDetector 中完成地理探测器的影响因子分析，在GWR 4.0中完成GWR分析，用ArcGIS 10.6 软件分别对研究区不同粒径砾石进行GWRK 插值，常规统计分析和绘图处理分别在Excel 2016和Origin 2017中进行。

2 结果与讨论

2.1 砾石粒径占比的描述性统计

表2是压砂地102个采样点砾石覆盖层砾石粒径占比的描述性统计特征值，各样点砾石粒径＞50、31.5～50、25～31.5、16～25、10～16、5～10、2～5 mm 和≤2 mm 平均占比分别为3.40%、3.98%、4.76%、7.33%、11.56%、15.09%、22.36%和31.52%。经典统计学通常用变异系数（CV）的大小描述变量的变异程度，当CV≤10%时为弱变异，当10%＜CV＜100%时为中等变异，当CV≥100%时为强变异[25]。表2结果表明砾石粒径占比的变异程度随粒径的减小逐渐减小，＞50 mm砾石CV最大，为59.62%，≤2 mm 砾石CV最小，为19.82%，所有粒径砾石占比均属中等变异，说明不同粒径砾石含量受随机性因素和结构性因素共同影响。通过K-S检验可发现仅＞50、5～10 mm和≤2 mm粒径砾石属正态分布，其余5 个粒径范围的砾石均不符合正态分布，说明不同粒径砾石含量受人为干扰较大。为满足地统计分析要求，对不符合正态分布的粒径进行对数正态转换，使其符合正态分布。

表2 不同粒径砾石占比的描述性统计Table 2 Descriptive statistics of gravel proportion with different particle size

2.2 基于地统计学的不同粒径砾石空间变异特征

在GS+9.0 中对压砂地不同粒径砾石占比进行半方差函数模型拟合，结果如表3 所示。参照半方差函数理论模型的选取标准（决定系数R2接近于1、残差RSS趋近于0），发现粒径＞50、31.5～50、25～31.5、16～25、10～16、5～10、2～5 mm 和≤2 mm 的砾石含量适宜的模型分别为指数模型、线性模型、纯块金模型、指数模型、线性模型、高斯模型、线性模型、球型模型。砾石的空间变异性受结构性因素和随机性因素的共同影响，结构性因素（砾石母质、地形等）会导致空间相关性增强，随机性因素（耕作制度、种植年限等）使砾石空间相关性减弱[26]。在8 个粒径砾石中2～5、10～16 mm 的砾石空间异质比均大于75%，说明其受随机性因素影响剧烈；25～31.5 mm 的最佳模型为纯块金模型，说明其空间上呈随机性分布；其余粒径的空间异质比均小于25%，说明结构性因素是空间分布的主导因素。变程结果显示10～16、2～5 mm 粒径的变程均远大于平均采样间距（250 m），说明相较于其他粒径砾石，10～16、2～5 mm 砾石的空间连续性的尺度范围更大。

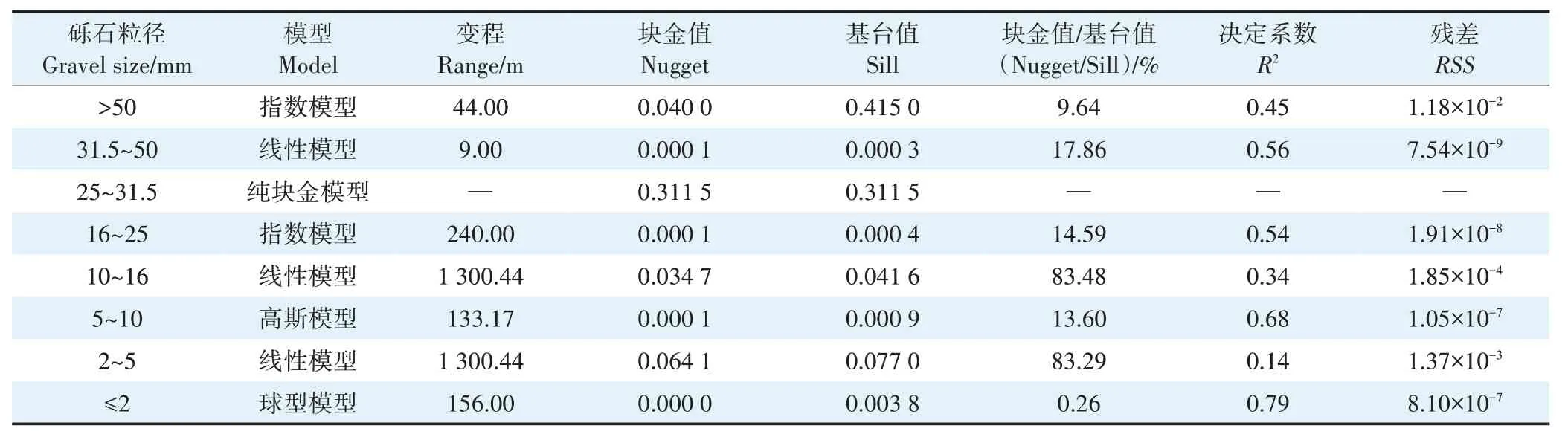
表3 压砂地不同粒径砾石占比的半方差模型参数Table 3 Semivariance model parameters of gravel proportion with different particle size in gravel-sand mulched field

2.3 Moran′s I指数

图2 为通过GeoDa 软件获取的不同粒径砾石全局Moran 散点图，全局Moran′sI指数为Moran 散点图的斜率。对压砂地不同粒径砾石进行全局空间自相关分析发现，砾石粒径范围为＞50、31.5～50、25～31.5、16～25、10～16、5～10、2～5 mm 和≤2 mm 的全局Moran′sI指数分别为0.892、0.717、0.928、0.924、0.923、0.674、0.944和0.779，各粒径砾石的全局Moran′sI值均高于0.674，P均小于0.01，表明压砂地不同粒径砾石均表现出很强的空间正相关，且Z值均大于1.96，表示空间相关性显著，说明样点与周围样点的值相似。在Moran散点图中，数据处在第一、第三象限表示正的空间自相关性，数据处于第二、第四象限表示负的空间自相关性。由图2可知，各粒径砾石的散点分布状况不同，但整体均主要分布在第一、第三象限，说明其在空间分布上并非完全随机，而是具有极显著的空间依赖特征，即各粒径砾石在空间上呈显著聚集性。

图2 不同粒径砾石占比的空间自相关分析Figure 2 Spatial autocorrelation analysis of gravel proportion with different particle size

2.4 压砂地不同粒径砾石空间分异的因素识别

本研究利用地理探测器的因子探测器得到种植年限、坡度、坡向、地表粗糙度、地表起伏度、剖面曲率及平面曲率7 个可能影响压砂地不同粒径砾石空间分异因素的q值并对其进行了排序（表4），各个因子的解释力均通过了1%的显著性水平检验。对各因子的平均q值综合分析可知，影响压砂地不同粒径砾石空间分异的因子按影响大小依次为种植年限＞坡向＞地表粗糙度＞坡度＞剖面曲率＞平面曲率＞地表起伏度。

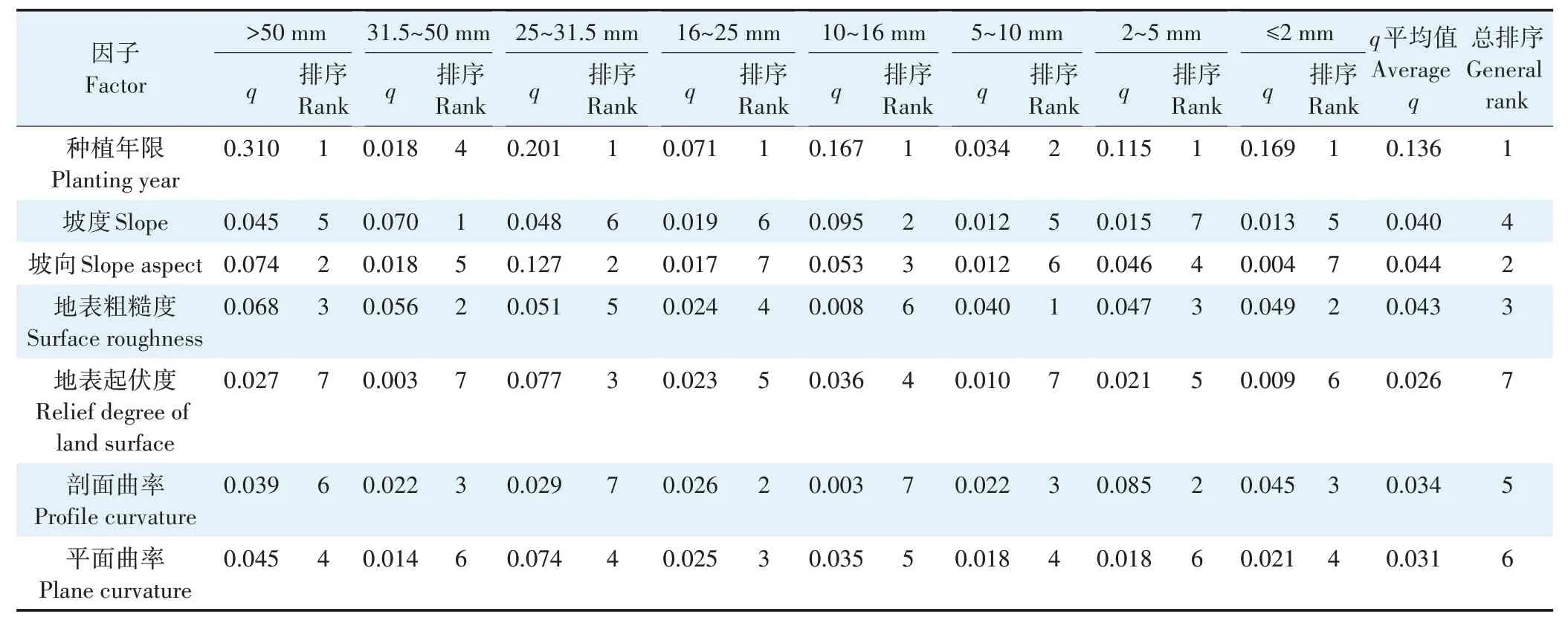
表4 压砂地不同粒径砾石占比空间分异的因子探测结果Table 4 Factor detection results of spatial differentiation of gravel proportion with different particle size in gravel-sand mulched fields

2.5 压砂地不同粒径砾石的空间分布特征及精度评价

GWR 模型通过计算回归模型的局部参数来消除地理数据中存在的空间自相关性及空间非平稳性问题，克服了回归模型中不同空间位置的环境因子权重一致的不足，实现了局部空间信息的捕获，提高了插值精度，同时其在空间制图方面表现出更丰富的局部细节和更光滑的空间渐变特征[27]，因此可以更加直观揭示出压砂地砾石配比的空间分布特征。

本研究在地理探测器识别压砂地不同粒径砾石空间分异因子的基础上，选取q值最高的三个因子（种植年限、坡向和地表粗糙度）作为GWR 模型的环境变量，并通过地理加权回归克里格法（GWRK）插值获取研究区压砂地砾石分布图（图3）。≤2 mm的砾石占比高值主要集中于研究区中部，西南部含量较低。2～5 mm 砾石占比高值区和低值区均呈破碎化、分散化分布。5～10 mm 和10～16 mm 砾石占比分布呈现相似的分布格局，高值均分布于东北部，低值集中分布于中部；16～25 mm 砾石占比高值区主要分布于西部和西南部，低值区主要集中于东北部；25～31.5 mm 砾石占比高值主要分布于西南部，东北部有零散分布，低值主要分布于中部；31.5～50 mm砾石占比的低值主要分布于东北部，其余部分均有明显高值分布；＞50 mm砾石占比主要集中分布于中部、西部及南部。

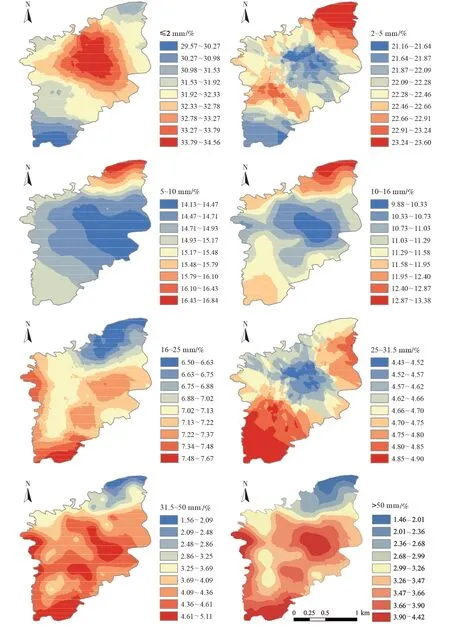
图3 不同粒径砾石占比空间分布状况Figure 3 Spatial distribution of gravel proportion with different particle size

本研究通过计算22 个验证点的MRE和RMSE来检验的GWRK 的插值精度，评价结果如表5 所示。＞50、31.5～50、25～31.5、16～25、10～16、5～10、2～5 mm和≤2 mm 粒径砾石占比的MRE和RMSE均趋近于0，说明引入种植年限、坡向和地表粗糙度三个影响因子的GWRK 模型能够较为精准地模拟压砂地不同粒径砾石的空间分布状况，同时也可以验证种植年限、坡向和地表粗糙度为压砂地不同粒径砾石的主要影响因子。

表5 GWRK精度评价Table 5 Accuracy evaluation of GWRK

2.6 不同粒径砾石占比的空间分布规律的成因分析

地统计分析表明不同粒径砾石的空间异质性受随机性因素和结构性因素共同影响，通过地理探测器进一步分析发现，种植年限、坡向、地表粗糙度、坡度、剖面曲率、平面曲率、地表起伏度均对砾石占比的空间分布产生不同程度的影响。

随种植年限增加，压砂地砾石层中大粒径砾石占比逐渐降低而小粒径砾石占比逐渐提高。相关研究表明影响砾石分布的原因主要有地表径流、风蚀风化及人为活动干扰[13，28]，研究区处于干旱半干旱带，降雨稀缺，自然条件下难以形成地表径流，因此仅有小粒径砾石和细土可能在农业灌溉作用下向下迁移。风蚀风化作用对不同粒径砾石的分布有显著影响，坡向会影响太阳辐射的强度和时间，地表粗糙度表示地表对风速和风沙活动的影响，坡度、剖面曲率、平面曲率和地表起伏度均反映了区域微地形状况，均可影响砾石的风蚀风化进程[29]，导致不同位置的砾石在流水、风力及重力等外营力作用下砾石的空间分布有所差异。一些学者研究表明，坡度是砾石分布的重要影响因子[8-10]，压砂地不同粒径砾石空间分异的主导因素识别表明，本研究中坡度对不同粒径砾石分布的作用相对较弱，这主要是由于压砂地一般选取地表平整、地表起伏度较小的区域进行铺砂及后续农业耕作，因此研究区内各样点的坡度、剖面曲率、平面曲率和地表起伏度变化较小，对于砾石分布的影响相对较低。坡向的q值高于其他几个地形因子，这是因为研究区地貌类型为黄土丘陵，区内沟壑纵横，虽然压砂地所处位置一般为坡底，但其坡向存在差异，因此研究区内各样点所处位置的坡向成为影响侵蚀和风化的重要因子，对砾石的空间分布产生较大作用。种植年限的q值明显高于其他因子，说明不同粒径砾石的空间异质性受种植年限影响更为显著。这可能是由于种植年限增加，耕作过程中机械碾压和耖砂翻耕会加速砾石由大粒径向小粒径转化的过程，导致出现种植年限越大砾石破碎化越明显，以及土体中小粒径砾石占比提高的现象，谭军利等[30]也发现随着砂田种植年限延长，压砂地大粒径的砾石量减少，小粒径的砾石增多。

本研究从多个角度分析了压砂地土体中不同粒径砾石的空间分异及其影响因素，但不同因子的具体作用仍有待进一步探究。同时有必要针对不同种植年限压砂地土壤理化性质、土壤水分运动及溶质运移状况开展进一步研究，以期为实现压砂地农业可持续发展、恢复区域生态功能提供理论支撑。

3 结论

（1）不同粒径砾石空间变异系数为19.82%～59.62%，属中等变异，其空间变异性受随机性因素和结构性因素共同影响。

（2）不同粒径砾石占比的空间分布状况不同，各粒径砾石的全局Moran′sI值均高于0.674，并全部通过极显著性检验（P＜0.01），表明在全局尺度上压砂地不同粒径砾石均表现出很强空间正相关，即均存在极显著的空间依赖特征，且呈聚集性分布。

（3）压砂地不同粒径砾石空间分异的解释力由大到小依次为种植年限＞坡向＞地表粗糙度＞坡度＞剖面曲率＞平面曲率＞地表起伏度，种植年限、坡向和地表粗糙度为砾石空间分异的主要影响因子。