恒力簧片自动铆接机龙门机构疲劳寿命优化设计*

刘建飞 ，张克军

（辽宁机电职业技术学院黄海汽车工程学院，辽宁 丹东 118009）

恒力簧片自动铆接机的龙门机构是承受往复运动载荷的典型设备，其受载具有往复性、规律性和可统计性的特点。龙门机构的分析建立在应力与变形的理论基础上，还应该对其进行疲劳寿命分析。虽然应力分析结果比较小，但是往复载荷对疲劳寿命有着较大的影响，疲劳失效是需要重点考虑的环节[1]。根据疲劳寿命计算原理，利用有限元分析软件对龙门机构进行了研究，在分析应力与形状关系的基础上，得到疲劳寿命分析结果，选取疲劳寿命的薄弱环节，布置了优化设计方案，为恒力簧片自动铆接机的研发提供了研究方法和数据支撑。

1 理论背景

1.1 疲劳寿命统计理论背景

疲劳寿命统计分析是针对内部应力达到疲劳极限后的数据分析，随着设备运行期限的增加，疲劳损伤累计到一定值后，零件也可能出现疲劳损坏。疲劳寿命的预测实质上是应用数学方法统计疲劳累积损伤值[2]，并将其与疲劳累积损伤极限值进行比较判断的方法。

1.1.1 线性疲劳累积损伤理论

线性疲劳累积损伤理论由Palmgram提出，经Miner优化而最后形成的法则。法则规定，当损伤累积到一定值时，机械零件发生失效。设试样在破坏前的总周期数是N，则在某一周期数是n1、n2……nn，则损伤值：

当D=1时，零件失效。假设机械的关键零件出现疲劳失效时，吸收的能量值为W，由累积损伤理论统计得出Miner判断法则的表达式。若损伤累计值小于1时，Miner判断法则的表达式为：

1.1.2 非线性疲劳累积损伤理论

大批科学实验证明，人类疲劳积累受伤规律性中存在着不确定性的特征，所以目前对非线性累积磨损规则的数学模型仍在研制之中。Henry损伤理论假设，当劳累与伤害累积到足够量的循环次数时，材料就会产生损伤，其P-S-N曲线发生改变，损伤表达式定义为：

式中，SL为原始材料的疲劳极限；S”L为受载后材料的疲劳极限。

1.1.3 双线性疲劳累积损伤理论

双线性疲劳累积损伤理论假设，任何零件的疲劳都可分为三个阶段，分别为初始寿命阶段、扩展寿命阶段和瞬时断裂寿命阶段，因此疲劳寿命应该按照不同的疲劳寿命统计方法进行计算。Manson疲劳预测方式是基于双线性累积损伤理论形成的，假设疲劳失效的初始阶段寿命为N1i，后期阶段寿命为N2i，计算表达式为：

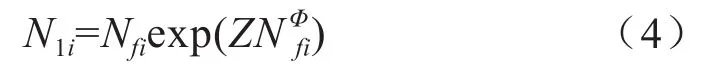
1.2 可靠性分析理论背景

机械可靠性设计中常用的数理统计方法有二项、泊松、正态、对数正态、威布尔和指数分布等多种函数。其中正态分布最为常用，很多自然现象或者科学问题都可以用正态分布来表示。正态分布的概率密度函数和累积分布函数分别为：

需要注意的是，随着制造能力的提升，正态分布的标准差得到降低，但是依然是典型的正态分布。

在机械设计及理论中，可靠度是重要的技术指标之一。可靠度是指产品实现一个特殊性能的概率，其表达式为：

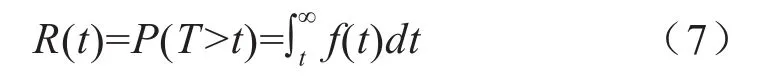
式中，R(t)为可靠度；f(t)为概率密度函数。

在安全性评价中，机械零件损坏程度的评价通常根据抗拉强度和极限性能判断。当抗拉强度超过极限后，不能引起损伤，否则将引起损坏，若使机械零件正常运作，应符合下列要求：

式中，S为零件的强度；s为零件所受的最大应力。假设应力与刚度遵循正态分布定律，则可靠度计算公式可转换为：

式中，µS为强度的均值；µs为应力的均值；σS为强度的标准差；σs为应力的标准差。

2 恒力簧片自动铆接机多体龙门机构有限元分析

2.1 建立多体龙门机构有限元模型

建立多体龙门机构的有限元模型是疲劳寿命分析的关键步骤，有限元模型的合理划分决定着有限元分析结果的可信性。导入装配完成的龙门机构模型，赋予各个零部件的材料特性，由于导入的装配体的零部件之间存在装配关系，在网格划分时，零件与零件之间的边界不能进行统一计算，所以需要对龙门机构的装配体进行一体化处理。利用组合体操作对多体机构进行一体化处理，选择四节点四面体单元对龙门机构进行网格划分[3-5]，得到模型如图1所示。由图1可知，龙门机构的有限元模型由133 235个节点、81 510个单元组成，网格疏密合理。

图1 龙门机构的有限元模型

2.2 龙门机构有限元分析结果

基于恒力簧片自动铆接机的实际工作状态，对龙门机构的支撑腿处设置约束，加载载荷，对其进行求解，设置求解对象为等效应力和变形。通过有限元软件的后处理模型，设置求解参数，分别得到龙门机构的等效应力云图和变形云图如图2和图3所示。由图2和图3可知，龙门机构的等效应力最大值为170.99 MPa，变形最大值为0.176 89 mm，基于公式（5）～（9），得到可靠度为0.987 2。

图2 等效应力云图

图3 变形云图

3 龙门机构疲劳寿命分析

实验和软件统计是疲劳寿命预测的主要方法，实验统计法需要产品设计完成投入生产后才可进行，并且对于结构复杂的箱体类零件的疲劳寿命研究存在较大困难，实验周期长。随着计算机技术和仿真技术的发展，软件计算法在近年来应用越来越广泛，在刚柔耦合虚拟样机中可以简单地提取载荷谱进行疲劳寿命分析，并结合具有指定存活率的P-S-N疲劳寿命曲线进行疲劳寿命分析，不仅缩短了生产周期，在保证疲劳寿命的同时，还可以优化结构，提高使用率。常用的疲劳寿命分析软件有ANSYS、Fe-safe、MSCFatigue和Nsoft等等。在ANSYS中加载龙门机构的应力和变形等结果，在材料库中查找并调取材料特性曲线，加载到疲劳寿命分析模块中[6-8]，设置求解参数，进行计算，得到恒力簧片自动铆接机龙门机构的疲劳寿命云图如图4所示。由图4可知，龙门机构疲劳寿命为20 089次，在往复循环载荷的作用下，龙门机构寿命较短，需要对其进行优化，增加其疲劳寿命，进而提高恒力簧片自动铆接机的工作效率。

图4 龙门机构疲劳寿命云图

4 龙门机构疲劳寿命优化设计

选取疲劳寿命值较低的两处关键位置为优化设计区域[9]，对其结构进行优化设计，龙门机构优化位置一采用十字形焊接加固，优化位置二采用三角形加固[10-11]。由于ANSYS建模功能并不具备优势，所以利用三维建模软件建立优化后的龙门机构，重新建立的优化后关键位置示意图如图5和图6所示。

图5 优化位置一

图6 优化位置二

对优化后的龙门机构重新进行有限元分析和疲劳寿命分析，得到优化后的龙门机构的等效应力最大值为102.5 MPa，变形最大值为0.097 922 mm。优化后的疲劳寿命云图如图7所示，与优化前相比较，疲劳寿命由20 089次提高到130 910次，优化效果显著，龙门机构的性能得到提高。

图7 优化后的龙门机构疲劳寿命云图

5 结论

基于疲劳寿命统计理论，利用有限元分析软件ANSYS，对恒力簧片自动铆接机龙门机构进行疲劳寿命优化，结果如下：

1）恒力簧片自动铆接机龙门机构的等效应力最大值为170.99 MPa，变形最大值为0.176 89 mm。在应力和变形分析的基础上，进行疲劳寿命分析，得到龙门机构疲劳寿命为20 089次，寿命较短，需要对其进行优化，增加其疲劳寿命。

2）基于疲劳寿命分析结果，选取关键区域进行优化设计。结果表明，与优化前相比较，优化后的龙门机构疲劳寿命由20 089次提高到130 910次。