生活中的平移实例剖析

汪二梅

数学源于生活，又应用于生活。生活中处处有平移，恰当地利用平移变换来解决数学问题，往往可以起到事半功倍的效果。

例1 如图1，中央商场重新装修后，准备在大厅主楼梯上铺设某种红色地毯。已知这种地毯每平方米售价30元，主楼梯道宽3m，其侧面如图1所示，则购买地毯至少需要多少元？

若要通过逐步计算，比较复杂。我们可以先利用平移的知识，将楼梯水平方向的线段沿竖直方向分别平移到BC上，竖直方向的线段沿水平方向分别平移到AC上。于是，铺地毯的横向线段的长度之和就等于横向直角边的长度，纵向线段的长度之和就等于纵向直角边的长度。所以，地毯的总长度至少为4.6+2.4=7（m），总面积为7×3=21（m2），所以购买地毯至少需要21×30=630（元）。

我们运用平移的知识，把要求的所有线段平移到一条直线上进行计算，问题就变得容易多了。因此，同学们在学习平移知识时，一定要用心去体会。

例2 如图2，在宽为20m、长为30m的长方形花园中，要修建两条宽为1m的长方形道路，余下部分进行绿化，请求出绿化部分的面积。

同学们常用原大长方形的面积减去两个小长方形（即两条道路的面积），再加上一个边长为1m的小正方形的面积求解。

但上述过程比较复杂，如果应用平移，则简便许多。具体做法是：将两个小长方形（即两条路）分别平移到长方形的上边和右边，即把分散的内容集中到一块儿，让计算简单化，如图3。这里通过平移变换，避免了对图形的分割，使求解更简洁、方便。

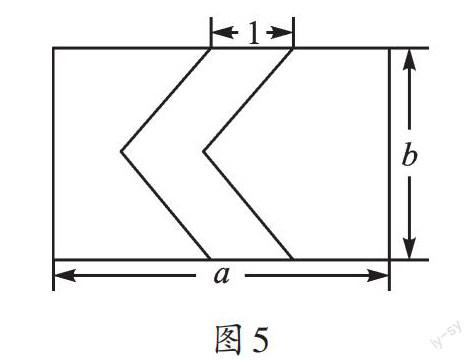
拓展 如图4—图6，在一块长方形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位），请你猜想空白部分表示的草地面积分别是多少？

只要小路宽度处处相等，我们也可以通过平移得到相同的结果。图4—图6都可以通过平移得到图7。

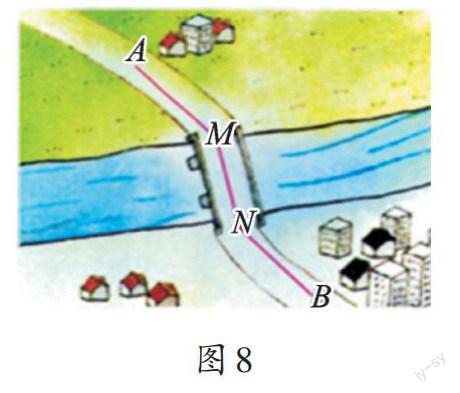
例3 如圖8，A、B两地在一条河的两岸，现在要在河上造一座桥MN，桥造在何处才能使从A地到B地的路径AMNB最短？假定河的两岸是平行的直线，桥要与河垂直。

A、B两地在河的两侧，且连接AB的线段不垂直于河岸。如图9，我们不妨先将点A沿垂直于河岸的方向平移到点A′，使AA′的长等于桥长MN，然后连接A′B与河岸P交于点N，再过点N作MN垂直河岸l，连接AM，则AMNB的长为满足条件的最短路线。

在这里，我们应用了“两点之间线段最短”和平移变换，但实质是相等的边之间的转化和平移的性质的应用。我们还运用了一种探究问题的方法，即先假设图形已作出，探究出解题思路后，再去解题。

（作者单位：江苏省连云港市新海初级中学）