用三面角模型巧解2022 年高考立体几何题

华南师范大学附属中学(510630) 周建锋

在立体几何中,求空间角是一个难点,特别是线面所成的角和二面角,让许多中学生头痛.究其原因,空间角由于是一个三维结构,而展示给我们的是画在一个平面上的图形,这就需要我们充分发挥空间想象能力,其难度无疑上升了一个层次.空间向量的引入虽然在很大程度上解决了问题,但它直接变成了一个演算模式,违背了立体几何培养学生空间想象能力的初衷.如何既能保证锻炼学生的空间想象,又能帮助他们减轻复杂程度? 立体几何问题解决的基本策略就是空间问题转化为平面问题、复杂问题转化为简单问题.

三面角是一个经典模型,文[1-4]及其它一些文章对三面角的几个定理均有论证,这里不再赘述.文[1]对二面角的定理作了较为全面的论证,并对线面角作了进一步研究,文[2-3]主要论述了角度大小比较或变化规律,文[4]主要运用了三面角余弦定理求二面角.笔者对三面角模型作了进一步的探索,并对三面角余弦定理作了进一步的拓展,同时把公式的格式做了优化.通过这两个定理及推论,我们发现,根据计算的难易程度,面角、线面角、二面角在适当的时候可以互相转化,以达到空间问题转化为平面问题,复杂问题转化为简单问题的目的.

一、三面角模型

如图1,由空间一点O引出的不共面的三条射线OA,OB,OC,可构成三个面角(∠AOB,∠BOC,∠COA),三个线面角(OA与平面BOC所成的角,OB与平面COA所成的角,OC与平面AOB所成的角),三个二面角(B-OA-C,C-OB-A,A-OC-B),我们称之为三面角模型O-ABC.

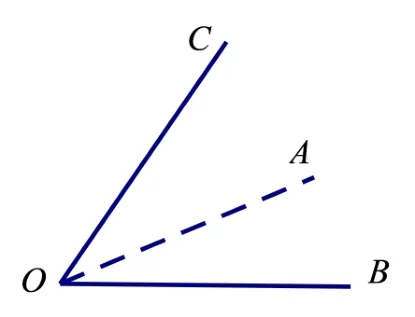
图1

为叙述方面,不妨记∠BOC,∠COA,∠AOB分别为α1,α2,α3,OA与平面BOC所成的角为β1,OB与平面COA所成的角为β2,OC与平面AOB所成的角为β3,三个二面角B-OA-C,C -OB-A,A-OC -B分别为γ1,γ2,γ3.

二、利用三面角模型求解高考题

利用三面角模型,我们在求解立体几何问题时有如下转化策略:

1.线面角的转化

(1)通过定理2,可以把线面角的计算转化为一个面角和一个二面角的计算(存在两个方向可以转化),我们可以选择一个易于计算的二面角.

(2)通过定理1,还可以把其中的二面角进一步转化为面角的计算,这样线面角计算也可以转化为三个面角的计算.

2.二面角的转化

(1)通过定理1,可以把一个二面角的计算完全转化为面角的计算.

(2)当存在两个平面垂直时,通过定理1 推论2,还可以把二面角的计算进一步简化为两个面角的计算.

(3)通过三面角正弦定理,可以把二面角的计算转化为另一个二面角加两个面角的计算,我们可以选择一个易于计算的二面角.

通过这样的转化,计算及作辅助线的难度降低,但仍然需要对空间的线面关系有清晰的认识,同样能达到锻炼空间想象能力的目的.

在具体运用两个定理及推论时,往往有更加灵活的转化方式.下面以2022 年高考题为例谈谈两个定理及推论在求空间角中的应用.

例1(2022 年高考浙江卷) 如图2,已知正三棱柱ABC -A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F -BC-A的平面角为γ,则()A.α≤β≤γB.β≤α≤γC.β≤γ≤αD.α≤γ≤β

图2

分析不妨设正三棱柱棱长为1.如图3,过点F作FG//AA1,交AC于点G,连结GE,则∠EFG=α,∠FEG=β.则在RtΔEFG中,易知FG=1,GE≤1,所以α≤β.在三面角模型E-BFG中,sinβ=sin ∠FEBsinγ≤sinγ,易知γ为锐角,则β≤γ.

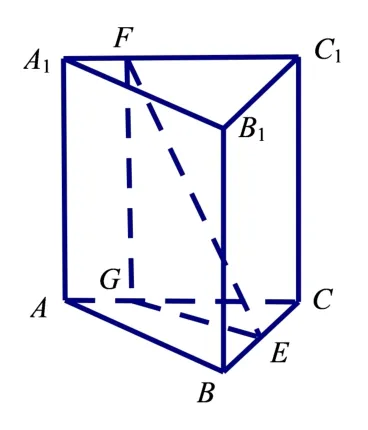
图3

综上得:α≤β≤γ,应选A.

例2(2022 年高考甲卷理科) 如图4,在四棱锥P-ABCD中,PD⊥底面ABCD,CD//AB,AD=DC=CB=1,AB=2,DP=

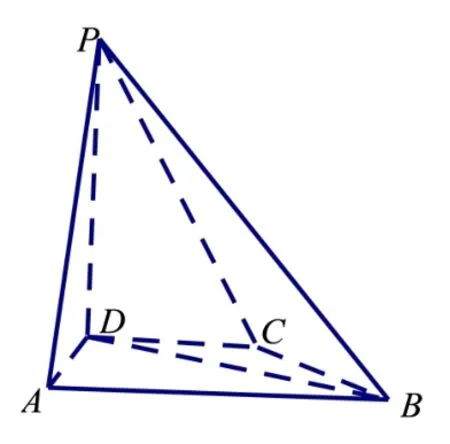
图4

(1)证明:BD⊥PA;

(2)求PD与平面PAB所成的角的正弦值.

(1)略.

(2) 分析1如图5,在三面角模型P -ABD中,所求线面角有两条转化路径:∠DPA及二面角D -PA-B,∠DPB及二面角D-PB-A.相比之下,路径1 更易于计算.设PD与平面PAB所成的角为β,二面角D-PA-B大小为γ,由定理2,sinβ=sin ∠DPAsinγ,由已知,PD⊥平面ABCD,则RtΔPAD中,sin ∠DPA=.

图5

(Ⅱ) 再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.条件①:AB⊥MN;条件②:BM=MN.

注:如果选择条件①和条件②分别解答,按第一个解答计分.

图6

(Ⅰ)略.

(Ⅱ)分析只看条件①(条件②同理),则AB⊥MN.在三面角模型B-AMN中,考虑将线面角转化为面角∠ABN和二面角A-BN -M的计算,而这两个角均易于计算.设直线AB与平面BMN所成角为β,二面角A-BN -M大小为γ,则sinβ=sin ∠ABNsinγ.如图7,取AB中点D,连结MD,ND,则MD//BB1.

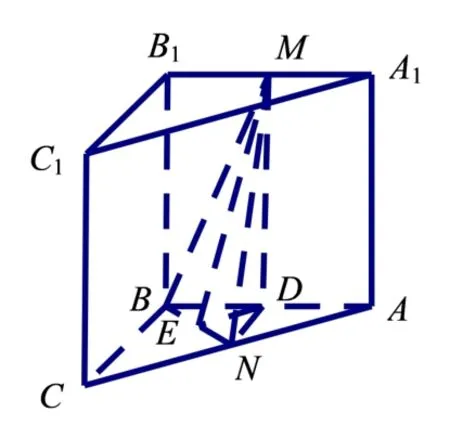
图7

例4 (2022 年高考全国Ⅰ卷) 如图8,直三棱柱ABC -A1B1C1的体积为4,ΔA1BC的面积为

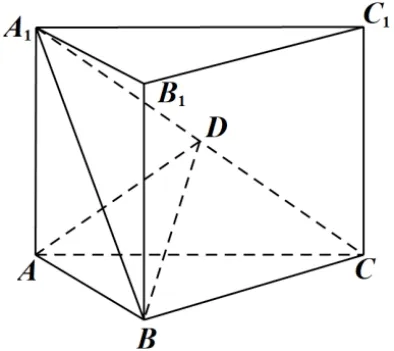
图8

(1) 求A到平面A1BC的距离;

(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.

(1)略.

(2) 分析1 由三面角模型B -ACD,设二面角A-BD-C大小为γ,则由定理1 得到

例5(2022 高考全国ⅠⅠ卷) 如图9,PO是三棱锥P -ABC的高,PA=PB,AB⊥AC,E是PB的中点.

图9

(1)求证:OE//平面PAC;

(2)若∠ABO=∠CBO=30°,PO=3,PA=5,求二面角C-AE-B的正弦值.

图10

(1)略.

(2)分析1设二面角C -AE-B大小为γ,在三面角模型A-BCE中,由定理1,

分析2设二面角C -AE -B大小为γ1,二面角E-AC-B的大小为γ2,由定理2 推论,,而γ2相比γ1更易于计算.由前所得:∠CAB=90°,sin ∠EAB=

如图11,过F向AC作垂线,垂足为G,连结GE,易知∠EGF=γ2.可算得GF=,GE=sinγ2=,所以sinγ1=

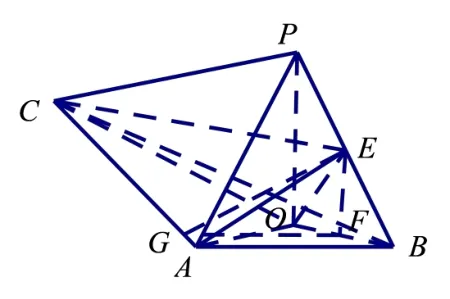
图11

通过对2022 年全国高考立体几何题的分析,可以看出,在求解线面角或二面角时,利用三面角模型,我们有更加灵活的转化途径,两个定理及推论也可以互相结合,构造出更易求解的解题途径.