2022 年新高考Ⅰ卷填空题试题分析与教学启示

广东佛山南海中学(528211) 周鸿高

一、试题呈现

2022 年新高考Ⅰ卷数学试题填空题如下:

二、试题解读

第13 题解读题干“(1-)(x+y)8”由两部分:(1-),(x+y)8构成,其中(x+y)8可应用二项式定理展开,然后再每项乘以(1-),合并同类项后得到结果.试题主要考察考生对二项式定理的理解,并能简单应用.试题设置简单直接,但由于(1-),有两种情况,且出现“负号”,以及组合数的计算(题干注明“用数字作答”),会给部分考生造成一定的解题失误.本题体现基础性,属于中低档题.

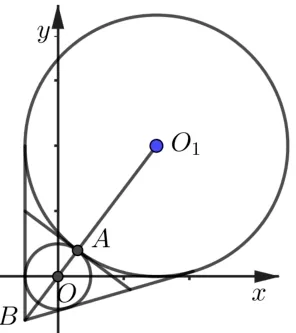
第14 题解读题干给出两个圆的方程,写出一条公切线方程.求两圆的公切线方程,需要先判断两圆的位置关系,因为不同位置关系的两圆公切线情况不一样.考生如果直接求解公切线方程,将陷入繁琐的计算过程.事实上,如果先判断出两个圆是外切的位置关系,再画出图形,可以发现“直线x=-1”与两个圆相切,这是最容易得到的公切线,由于“直线x=-1”的斜率不存在,直接求解反而求不出.另外,教材例题指出,当两圆相交时,两圆方程相减为相交弦所在直线方程,不难类比得到,当两圆相切时,两圆方程相减就是切线方程,本题直接把两圆方程相减就可以得到内公切线方程.这是一道有限制范围的开放性试题,能够较好考察考生的分析问题能力、迁移知识能力,达到较高区分度的目的.本题体现创新性.

第15 题解读曲线方程含有参数,已知曲线存在两条过原点的切线,求参数.这是一道“逆向”的问题,需要先求含参数的切线方程,再代入原点坐标,得到关于x的方程,有两解.关于x的方程是一元二次方程,则需要满足条件Δ＞0.本题需要求导,设切点,列出切线方程,代入化简,考察考生较强的运算转化能力,综合性较强.不过解题方法常规常见,化简后的方程是一元二次方程,是考生很熟悉和掌握的.如果考生采用分离变量的方法求解,则需要分类讨论.本题体现应用性.

第16 题解读本题综合性较强,需要先由离心率为发现等边三角形(即a=2c),据此得到直线DE是AF2的中垂线,因此AD=DF2,AE=EF2,等量代换后,结合椭圆定义,得到所求三角形周长为4a;再利用弦长、离心率和椭圆方程,计算出a的值.考察考生较强的分析转化能力、运算求解能力.本题应用常规方法解答,运算求解过程比较繁琐,很考验学生的数学功底.另外,本题隐性考察椭圆的第二定义、焦半径、极坐标方程(焦点弦)等高阶的圆锥曲线知识方法,考生如果接触过这些知识方法,并能在考场上应用,可以简化运算求解过程.

三、答题情况

1 试题答案

第13 题:-28.

第14 题:x=-1 或3x+4y-5=0 或7x-24y-25=0.

第15 题:(-∞,-4)∪(0,+∞).

第16 题:13.

2 典型错误

四、试题评价

教师对填空题组的认可度:起点较高,计算量大,需要考生具备较强的分析转化能力,能够考察考生的数学能力与数学素养.

第13 题需要两项合并,且涉及正负符号,作为填空题首题,起点较高,部分考生作答不理想.

第14 题虽然三条直线只写一条,且有几乎不用求解的“直线x=-1”,但考生看到题目自然做法就是设直线方程y=kx+b,求解k,b,就会陷入繁琐的计算中,且不能算出直线x=-1,极容易出错.

第15 题是切线的逆向问题,涉及多字母(符号)运算,考生即使有正确的解题思路,解题过程也容易出错.

第16 题涉及点、线较多,需要进行转化,才能正确解题,而且解题过程也不是一蹴而就,需要较强的运算求解能力.

对比2021 年新高考Ⅰ卷填空题,计算量与思维量明显提升.2021 年填空题难题主要集中在第16 题,而且设置为递进式双空题,保证大部分考生第一空的得分;今年填空题第14题计算量大,第15、16 题需要较强的分析转化能力,且都是单空题,得分不如去年.

五、以题论教

下面笔者结合对填空题的解析,谈谈对今后高考数学的教考建议.

1.高中数学教学要着力于理解概念、原理,对必备知识要教透、学透,放慢高中数学新课的学习进度

统计发现,涉及数学概念、原理的考题,考生往往做得不好.考后评讲时,若提问相关数学概念、原理,能正确复述的学生寥寥无几,甚至有忘得一干二净的.而现在考题愈发命制在概念、原理处,解法也是回归最基本的方法.因此,新高考模式下要更加重视数学概念、原理的教学.一是要放慢学习的脚步:数学概念、原理对学生而言,大都抽象难懂,接受它、理解它需要时间,过快进入应用,是不可取的;二是从多层次多角度让学生理解概念、原理.以二项式定理为例,对二项展开式(a+b)n=的掌握,应从四方面进行教学:①公式本身的特点(认识公式);②公式基本的性质(理解公式);③公式本质的理解(推广公式);④公式相关的应用(应用公式).数学概念、原理的初次学习是极其重要和关键的,如果初次学习囫囵吞枣、半生不熟,“先入为主”的心理作祟将使得后来花再多的气力也“扭转”不了.

2.小题小做,善于用数形结合思想方法解题;小题巧做,善于用特值法、检验法、排除法、构造法解题;小题少做,善于利用二级结论、解题经验解题

考试答题讲究方法技巧,尤其对小题而言.数学小题指只要答案、不管过程的题型,一般指选择题和填空题.针对小题的这个特点,产生了许多专门“对付”小题的方法.

小题解题策略在高三备考过程中,要长期灌输、不断强化.教师评讲试题时,应该多做示范,多进行小题小做,数形结合,画图准确,分析快速到位;小题巧做,特值检验、构造排除,如何选取特值? 如何构造模型? 需要解题经验积累;小题少做甚至不用做,常见的二级结论、经典问题的解答,要积累熟记,尤其备考后期更适用.

3.通过题组的变式与拓展,引导学生多思考,提升分析转化能力;少进行简单重复的“刷题”,“刷题”只会让学生进行简单机械模仿,一旦考题稍作变化,考生就无所适从

以第15 题为例,考生考前都练过曲线在某点处的切线方程,进一步求过曲线过某点处的切线方程,再进一步已知曲线方程求参数值,也许自认为已覆盖切线方程的所有题型.然而考题却总能出人意料,本题已知曲线过原点的切线条数,求参数取值范围.其实解题思路与解法是一致的,相通的;如果平时能够进行题组的变式与拓展教学,引导学生多思考、多总结,一解多题,就能较好的应对这样的考题,否则,一旦面对这样有别于平时练习的考题,考生就会无所适从.事实上,本题的解答自然顺利:y′=ex(x+a+1),设切点为P(x0,y0),则y0=ex0(x0+a),k=ex0(x0+a+1),从而切线方程为y-ex0(x0+a)=ex0(x0+a+1)(x-x0),代入(0,0),得-ex0(x0+a)=-x0·ex0(x0+a+1),即x0+a=+ax0+x0,题意等价于方程+ax0-a=0有两个实根,则Δ=a2+4a ＞0,解得a ＜-4 或a ＞0.

再如第16 题,画出图形后,不能直接求ΔADE的周长,由e=,得a=2c,所以ΔAF1F2是等边三角形,直线DE是AF2的中垂线,则|DA|=|DF2|,|EA|=|EF2|,从而把ΔADE的周长等价转化为ΔDEF2的周长,即为4a.这个转化过程很关键,只有转化了本题才能解答,而一旦转化了,就是一道常见的试题.这是试题常考常新的变化之处,而这是“刷题”无法穷尽的.把握试题本质,提升转化能力,避免机械“刷题”,才能应对这些考题.

4.注重通法,优化解法,简化算法,提高解题速度

第16 题作为填空压轴题,从常规解法可以发现,解法常见常用,就是解答线锥问题的一般模型.这启示我们,通性通法是解答常规试题的基本方法,也是解答综合性强试题的压舱石.本题转化为解三角形不是解答该题的通性通法,但若是一道解三角形试题,即转化为解三角形后,其解法也是通性通法.高中数学解题教学,一定要重视通性通法的培养与训练,让学生形成各专题的一般解题路径.另外,二级结论的应用,高观点下的解法,对学有余力的考生,可以适时适当拓展学习,而且要学得比较通透.这样,面对综合性强的考题,“秘密武器”就成为最后的“杀手锏”,常能收到“奇效”.

高中数学学习与高考数学备考是一个系统工程,数学试题要解答得好,不仅要具备体系化的数学知识,要形成模型化的解题路径,还要培养敏锐的数学思维,善于调整答题的策略.高考数学试题越来越灵活,深入考察考生的数学核心素养.数学素养的培养不是一蹴而就的,也不是多解几道题就培养起来的,更不是会解几道数学题就养成了数学思维.数学素养的培养是一个长期的过程,新高考试题从侧面反映,高中的教育与学习应该慢下来,不要过于“急功近利”,脚踏实地沉下心来学习才是正确的学习之道.