例谈面积法在不等式证明中的应用

广州市第二中学(510530) 程汉波

深圳中学(518000) 朱华伟

面积法,作为一个古老的方法,是强有力的解题工具.张景中院士对面积法的研究几十年来可谓情有独钟,成果丰富且引人注目.特别地,学术研究上以面积法为基础的“消点法”在计算机上可以生成平面几何问题的“可读证明”,这一成果被称为计算机处理几何问题上的“里程碑”[1];教学研究上以面积为起点改造初中数学内部结构,在初一用面积引入正弦,然后以三角带动几何,串联代数,初中数学得以一线串通,这样的构想与方案得到中学教师的广泛认可并付诸教学实践,且取得了非常了得的教学成绩[2].本文结合具体实例,谈谈面积法在三角不等式、函数不等式、代数不等式和数列不等式证明中的应用.

1.面积法证明三角不等式

自面积与三角诞生之初,它们都与测量问题脉脉相通,面积源于人们对土地或物件大小的度量,三角又源于对三角形或圆中边、角、弧长关系或天文、航海等实际测量问题中的的研究.利用面积法可以巧妙地证明很多与三角不等式问题,譬如,被广大师生熟知的不等式:当0＜x ＜时,有sinx ＜x ＜tanx.一般在学习完三角函数定义的几何刻画“三角函数线”后即可作为挑战例题或练习.该不等式在学习完导数后当然可以给出简单一般的证明,但是或多或少损失了一些初等数学的巧妙美! 下面再给出一例以展示面积法在证明三角不等式问题中的巧妙运用.

例1设0＜x ＜y ＜z ＜,求证:+2 sinxcosy+2 sinycosz ＞sin 2x+sin 2y+sin 2z.

证明由二倍角公式知,原不等式等价于证明sinx(cosx-cosy)+siny(cosy-cosz)+sinzcosz ＜,(*)

如图1,设A(cosx,sinx),B(cosy,siny),C(cosz,sinz)为单位圆上第一象限内的三个点,分别通过这三个点作x轴、y轴的垂线得到三个矩形(图1 中阴影部分),事实上,(*)式左端即表示图1 中三个矩形的面积之和,它显然小于四分之一单位圆的面积,得证.

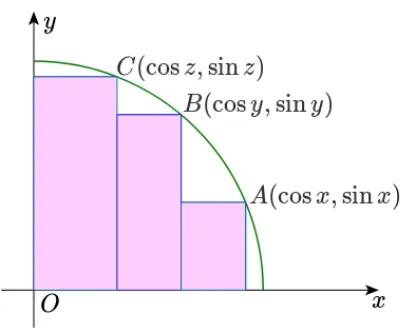
图1

单墫教授曾将该题在1990 年国家奥林匹克集训队中做过试验与统计:被检测的24 名优秀的中学生只有一个想到用面积法构图来解决[3].可见看似简洁巧妙的解法有时并不容易被发现.而且,他还用三角恒等变换的方法将该不等式加强为:若0＜x ＜y ＜z ＜,则+2 sinxcosy+2 sinycosz ＞sin 2x+sin 2y+sin 2z[3].另外,类似地利用面积法容易将该不等式推广到n元情形:设0＜x1＜x2＜···＜xn ＜,则+2 sinx1cosx2+2 sinx2cosx3+···+2 sinxn-1cosxn＞sin 2x1+sin 2x2+···+sin 2xn.

2.面积法证明函数不等式

随着微积分初步内容向高中的下放,及其一直以来在高考数学中压轴题的地位,函数不等式向中学的渗透也是水涨船高.函数与面积的联系也是一直被数学家所重视,例如,前文提到的张景中院士就利用单位菱形的面积引入正弦,重构三角,全局皆活,将初中数学一线串通[2].又如,林群院士和张景中院士还提倡在中学利用双曲线y=在u=1 与u=x之间与u轴所围成曲边梯形的“面积”来定义自然对数函数,由此可以很直观地推导出对数的运算性质,而且,该函数的学习时间点可以大大提前,甚至可以在初中学完反比例函数之后就进行拓展学习[4].下面再给出一例以展示面积法在证明函数不等式问题中的巧妙运用.

图2

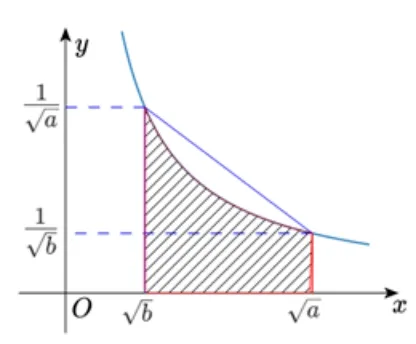
图3

3.面积法证明代数不等式

面积法与代数恒等式或不等式之间的关系在中学教材上屡次被关注,不论是初中学习平方差公式“a2-b2=(a+b)(a-b)”和完全平方公式“(a±b)2=a2±2ab+b2”等代数恒等式,还是高中学习的均值不等式“若a,b ＞0,则和二维形式的柯西不等式“若a,b,c,d ＞0,则(a2+b2c2+d2≥(ac+bd)2”等代数不等式,都有从几何直观的角度给出面积法证明,借以展示代数与几何的紧密相依.下面再给出一例以展示面积法在证明代数不等式问题的巧妙运用.

图4

图5

4.面积法与数列不等式

定积分的几何意义表示曲边梯形的面积,其定义涉及四个步骤:分割,近似代替,求和,取极限,在此即可窥见分割图形的面积之和与数列求和之间的联系.借此联系辅助以几何直观,搁置定义中取极限这一最后环节,曲边梯形面积可放大或缩小为容易计算的一系列小矩形面积之和,进而可以得到定积分所表示面积的上界与下界.这一想法的代数成果即可得到数列不等式,下面给出两例以展示面积法在证明代数不等式问题的巧妙运用.

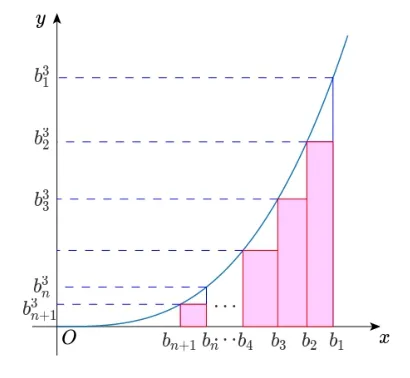
图6

由上观之,如果能够设法将欲证不等式以几何面积作为纽带,构造相应的几何图形,那么就可以将不等式的证明问题转化为几何图形面积的比较问题.这种由抽象的“式”到直观的“形”的转化,有时可使问题化难为易,起到事半功倍的效果.

“数”与“形”是数学中两个最基本的研究对象,而面积非常好地承载了它们的双重特征与优势,“以形助数”或“以数解形”,把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,使复杂问题简单化,抽象问题具体化,从而起到优化解题途径的目的.而且,在高等数学中,面积又以各种形式出现.面积是积分,是测度,是外微分形式,是向量的外积,也是行列式.因而,作为既古老又年轻的面积法,值得我们不断的学习与研究.