基于混沌浮点运算的医学图像加密方法与FPGA 实现*

庞 宇，魏 东，王俊超

（1.重庆邮电大学 光电信息感测与信息传输实验室 重庆 400065；2.重庆大学 微电子与通信工程学院，重庆 400044）

0 引言

目前，互联网技术的快速发展使电子医疗变得便捷可行和普遍流行。电子医疗提供了一种基于互联网系统的远程、在线就医技术。患者可以联系专家医生进行在线诊断。在线就医过程中，一些涉及患者隐私的医学图像数据需要通过互联网存储和传输，在此过程中可能会面临数据泄露问题。而数据加密是避免医学图像数据泄露、保护隐私的最佳方法。与普通图像相比，医学图像具有的冗余、数据量大、像素相关性大等特点[1−2]，使得类似于AES 等传统的加密技术对医学图像这类特殊格式数据的加密效率低下[3]。医学图像加密算法不仅需要很高的安全性，还需要可观的加密速度。

基于混沌算法的伪随机数生成器（Pseudo Random Number Generator,PRNG）生成的伪随机序列对初始值极度敏感、周期长、密钥空间大，与其他数据序列相比在安全性上具有明显的优势，用于医学图像加密具有很可观的加密效果[4]。除了算法严格性外，一种有效的加密系统实现技术可保证加密的速度得到提升。而硬件实现的方式在能够满足应用实时性的同时又可以防止运行算法的攻击[5]。现场可编程逻辑器件（Field -Programmable Gate Array，FPGA）以其高并行、可定制、能重构、低成本等特点十分适合于混沌加密算法的硬件实现[6]。

为了解决上述算法在实际医学图像加密应用中存在的问题，本文提出一种基于Logistic 映射浮点运算的伪随机序列生成方法用于加密医学图像从而达到提高加密强度的目的。考虑到加密实时性，在FPGA 上实现加密系统。混沌映射在有效保证加密随机性的同时，浮点运算能显著提升加密精度，扩大密钥空间。并对硬件加密系统进行稳定性测试，以及对密图数据进行统计分析，验证了算法的有效性以及硬件加密系统的稳定性。

1 密码系统设计

将医学图像数据输入到加密系统中，与PRNG 生成的伪随机数异或得到加密图像或原图数据。整个加密系统架构如图1 所示，加密的关键在于PRNG 的设计。

图1 加密系统框架图

1.1 引入浮点运算的Logistic 混沌系统

本文选择Logistic 映射作为混沌序列迭代算法，该算法结构简单，随机性好。方程式定义如式(1)所示：

式中，当控制参数μ∈[0，4]，可保证迭代值Xn∈[0，1]。随着μ值增大，系统出现不同的动力学行为，越接近于4[15]，迭代值在[0,1]之内分布越均匀。

数字计算机使用二进制数来表示数字，对于实数，有定点和浮点两种表示格式。浮点格式较之定点格式有更为宽广的动态范围，可以不用考虑数据的溢出和量化问题，因而可以缩短复杂算法的研发周期，与混沌系统结合可扩大混沌序列空间。

IEEE-754 标准定义了单精度(FP32)和双精度(FP64)两种浮点格式[16]，并将浮点数划分为符号位S、指数位E和尾数位F 三部分，各部分位数如表1 所示[17]。

表1 IEEE 754 标准浮点格式

在此文中设计了双精度浮点数运算迭代混沌序列可得到更高的精度。十进制μ和Xn用IEEE-754 表示：

其中：{Δx(i),Δy(i),Δθ(i)}来自里程计的观测值，{Ωx(i),Ωy(i),Ωθ(i)}是传感器噪声。

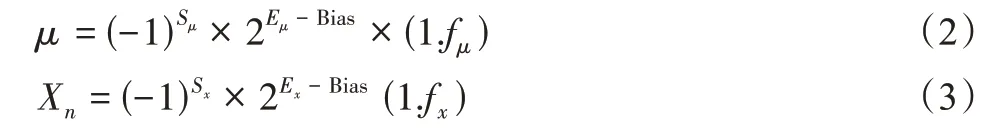
式(2)、式(3)中Bias 为指数偏移量，十进制表示为：则双精度指数偏移量为1 023。

混沌迭代过程涉及浮点数的减法和乘法运算模块，运算方程分别如下：

其中：m=(-1)S× (1.f)。

1.2 PRNG

为生成高质量的加密密钥，提出一种基于浮点数的PRNG 框架，如图2 所示,包括初始密钥输入、浮点混沌系统、随机序列量化三大模块。

图2 基于浮点数的PRNG 框架

初始密钥X0范围在(0,1)之间，双精度浮点格式表示在(0，3FF0000000000000) 之间。浮点混沌系统首先接收初始密钥，利用Logistic 混沌算法结合浮点运算迭代出浮点数格式的混沌伪随机序列Xn。利用阈值量化法将混沌随机序列Xn量化为单比特数据Sn(0,1)，具体量化方法是指将Xn与3FF0000000000000 比较，若大于此值则将Xn量化为1，否则为0。这种量化方式可有效继承原有序列的相关特性，并且量化后的输出结果难以推断出最初的混沌序列，可以提高安全性。

2 FPGA 加解密架构

在本文，所提出的基于FPGA 的加密系统流程如图3 所示。整个硬件加密系统在Altera 公司Cyclone IV EP4CE115F29C7N 开发平台上设计、综合以及验证。加密系统的硬件资源使用情况如表2 所示。初始密钥以及医学图像数据通过UART 串口通信模块依次进行传输。使能Load 以及复位后，初始密钥key_loaded[63∶0]通过Uart_rx 端口传输到PRNG 模块。在Logistic_Control 控制模块作用下PRNG 迭代出用于加密的密钥Xor_byte[7∶0]，再与医学图像数据Image[7∶0]进行异或加密，得到密图数据Enc_Image[7∶0]，并通过Uart_tx 发送出密图数据到PC。

表2 FPGA 硬件资源使用

图3 基于FPGA 的加密系统流程图

3 加密安全性分析

为了验证加密系统的可行性，用512×512 的Lena 灰色图像数据，在Altera 公司Cyclone IV EP4CE115F29C7 N 开发平台上进行加、解密。设置加密系统参数μ=64'h4010000000000000(4.0)，

初始密钥X0=64'h3FB999999999999A(0.1)。原图像、加密图像以及解密图像如图4 所示。结果显示无法从密图中识别出任何原图像信息。解密图像能够恢复明文信息。

图4 基于FPGA 的Logistic 混沌浮点加密过程

3.1 密钥敏感性分析

密钥敏感性表征了密码系统的安全性能。解密时，密钥微小变动便无法解密密文图像。为了检验加密系统的密钥敏感性能，对图像数据进行加密，研究在初始密钥上翻转一位，进行解密的效果。式（1）数据来源于将式（2）正确初始密钥数据尾数的第1 bit 翻转。式（3）将式（2）正确初始密钥数据尾数最后1 bit 翻转。分别将式（1）（2）（3）数据作为解密的初始密钥，对密图进行解密。解密效果如图5 所示。结果表明密钥仅改变1 bit便不能正确解密，十分敏感。

图5 初始密钥翻转1 位解密过程

3.2 统计分析

3.2.1 灰度直方图

图像的灰度直方图可以直观地显示每个灰度像素的统计特征[13]。从原图的灰度直方图可以很清晰看出图像像素值的统计特征。攻击者可以很轻易地从非均匀直方图中获取原图统计信息。而一种安全加密算法能够破坏原图像素值的统计关系，得到均匀分布的直方图，攻击者就难以从密图统计信息中获取原图相关信息。图6 测试了几组原始图像以及基于本文算法加密后密图的灰度直方图。经过对比验证了图像经过加密系统加密后灰度值分布无规律可循，加密性能良好。

3.2.2 相邻像素点相关性分析

为了进一步分析图像加密的效果，定性分析了图像原图与经过加密系统加密后的密图的相邻像素值，如图6 所示。图6 表明原图的两个相邻像素间存在极高的相关性。密图的像素值分布杂乱，相关性较低。也可用相关系数定量分析图像相邻像素的相关性，相关系数的计算过程如下:

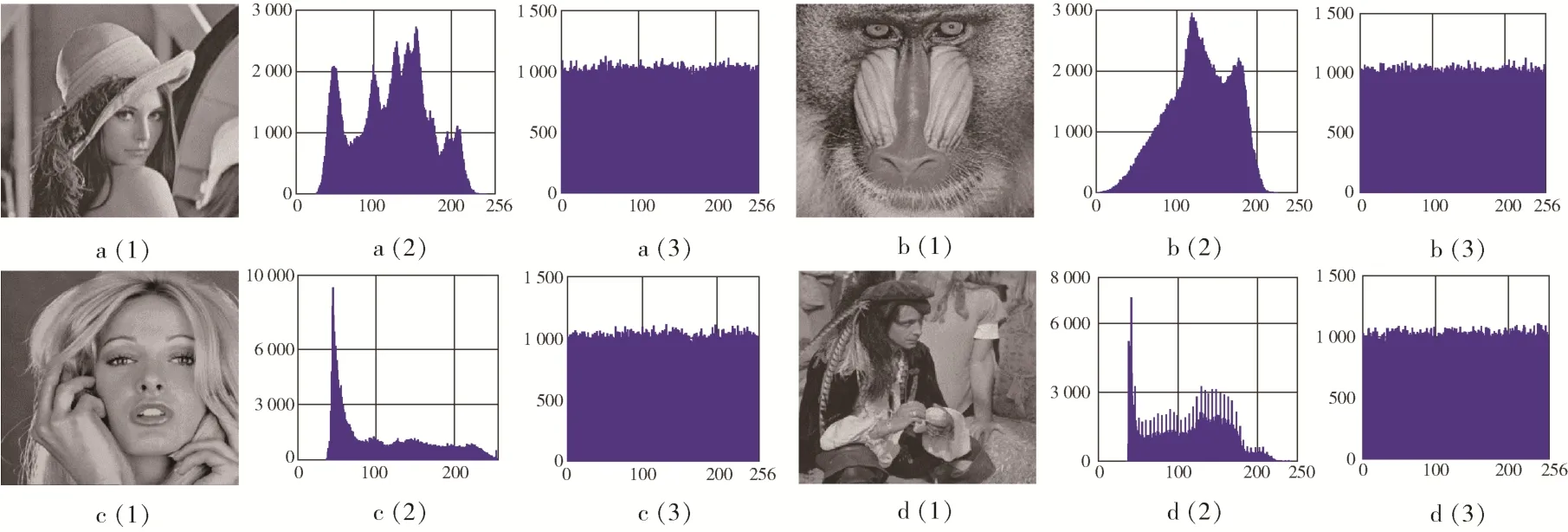
图6 各类图像加密前后灰度直方图

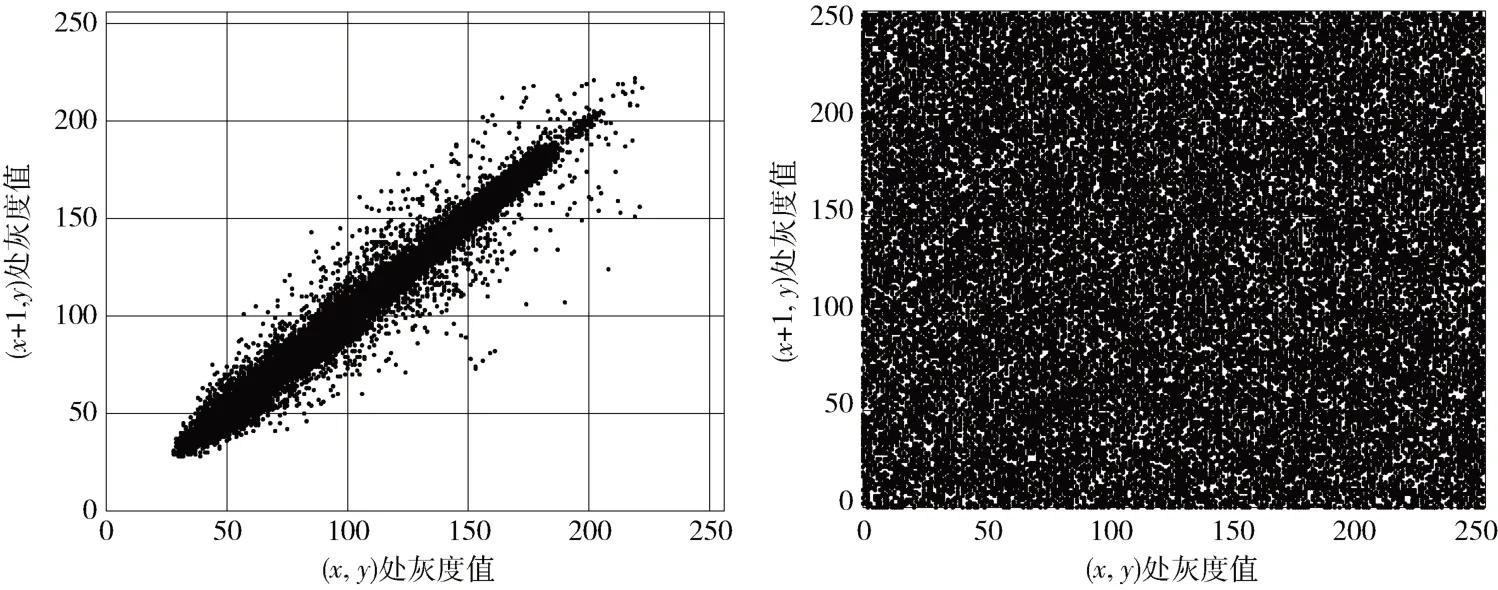
图7 Lena 图像加密前后相邻像素值分布

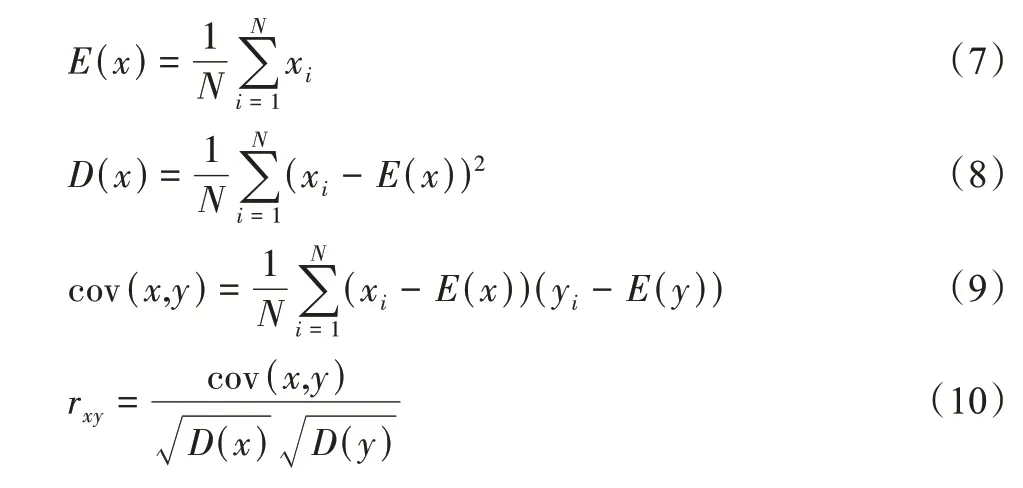
式中x、y是一对相邻像素值，E(x) 是平均值，D(x) 是平均方差，rxy代表相关系数，其值区间在[-1,1]之间。相关系数绝对值越低，加密效果越好。在表3 中将Lena 原始图像和经过本文算法加密后的图像从水平、垂直以及对角线三个方向上进行了相邻像素相关性系数计算，并与当前一些图像加密算法加密后相关系数计算结果进行了比较。可以看出图像加密前相关系数较高，接近于1，加密后图像相关系数很低，接近于0。

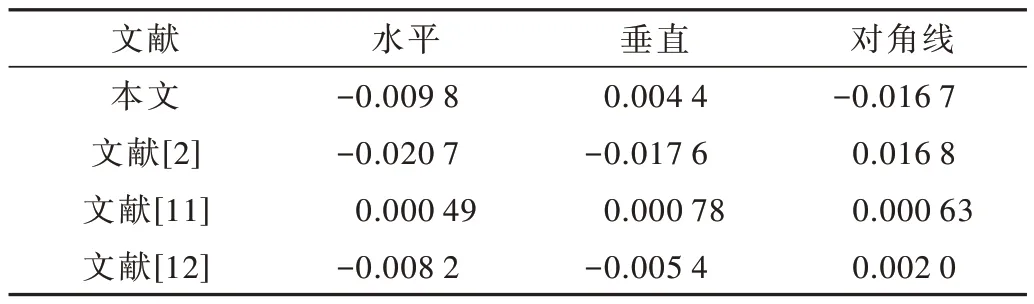
表3 图像的相邻像素相关系数

3.3 信息熵分析

信息熵反映了信息的不确定性。图像信息熵可以用来衡量加密后的图像的混乱程度，从而判断加密效果。信息熵的计算方法如下。

式中pi表示i发生的概率，对于灰度为256 的图像，信息熵越接近8，则它越接近随机图像。经过计算，表4 列出了本文Lena 密图的信息熵以及一些经过最新的图像加密算法加密后的密图的信息熵的对比。结果表明，基于本文算法计算的信息熵优于其他算法的信息熵。本文算法加密后的图像能有效降低成功攻击的几率。

表4 不同算法加密Lena 后的信息熵

4 结论

本文提出了将Logistic 混沌浮点运算作为基本随机序列迭代算法用于图像加密。在ED2-115 硬件平台上使用硬件描述语言Verilog 设计了基于上述算法的图像数据加解密系统，包括双精度浮点数运算。以Lena 标准测试图为例，对FPGA 硬件系统加密后的Lena 密图作安全性分析，实验验证了密图相邻像素相关性极低，信息熵达到7.999 3，接近于一幅随机图像，优于当前一些加密算法。并且整个FPGA 密码系统有较好的密钥敏感性以及系统稳定性。