一种基于线性规划的全局逃逸布线算法

陈 虹，陈传东，2，魏榕山

（1.福州大学 物理与信息工程学院，福建 福州 350108；2.福建省光电信息科学与技术实验室，福建 福州 350108）

0 引言

印制电路板（Printed Circuit Board，PCB）是集成电路（Integrated Circuit，IC）的载体[1]。随着大规模集成电路和超大规模集成电路的发展，PCB 的集成度要求越来越高，现有的电子设计自动化（Electronic Design Auto‐mation，EDA）工具已无法满足高密度引脚布线要求，一般与人工布线相结合，布线工作变得耗时且复杂[2]。因此，为了得到更高效的布线结果，EDA 自动布线算法成为近几年的研究热点。

传统意义上，PCB 布线分为逃逸布线（Escape Rout‐ing）和区域布线（Area Routing）[3]。逃逸布线是指将引脚按要求逃逸到组件边界，其作为PCB 布线的关键一环，对电路性能好坏和后期的区域布线起着决定性作用。区域布线是指将不同组件中对应功能的引脚实现互连，合法化的逃逸布线结果为区域布线阶段节省布线空间，并大大提升PCB 整体布通率。为实现更高的空间利用率，逃逸布线又可精细化分为有序逃逸布线（Or‐dered Escape Routing，OER）和无序逃逸布线[4]。

以往的工作中一般采用网络流方法解决无序逃逸布线问题[5−7]，然而网络流不能处理OER 问题，因为其并不携带有序信息，一般采用启发式算法叠加拆线重布进行布线[8]。Luo 等人首次提出了将OER 问题建模为平面布尔可满足性问题[9]，提出利用现有的布尔可满足性求解器进行求解，但其没有解决容量限制问题；2009 年，Yan 等人提出一种新的网络流模型建模[10]，在原本基础上解决了对角线容量建模的问题，但该模型有可能丧失大量最优解；2016 年，Jiao 等人首次提出将最小成本多商品流方法（Min-Cost Multi-Commodity Flow，MMCF）用于解决有序逃逸布线问题[11]，主要通过在原始网络流模型中加入大量虚拟中转节点，以满足有序逃逸布线的约束，并采用MMCF 求解器求解；最新的研究中，Jiao 等人将MMCF 模型充分扩展以求解差分对问题[12]，并首次考虑优化线长问题，但该模型由于加入过多的虚拟点，在求解大规模问题时，解空间规模过大，容易引起时间冲突。

本文主要讨论有序逃逸布线，即将PCB 上的所有待逃逸引脚按照一定的顺序逃逸到组件的边界，如图1所示。

图1 有序逃逸示例图

1 模型建立

1.1 问题描述

给定一个OER 实例R，包含了逃逸区域R 和待逃逸引脚集合Ρ。逃逸布线定义为：原始输入是一个m×n的针栅引脚阵列（Grid Pin Array，GPA），其中有n个待逃逸引脚P={p1,p2,p3,…,pn}，要求在满足指定布线约束下逃逸到指定边界，并输出所有逃逸路径Nets={net1,net2,net3,…,netn}。

多商品流问题是指将网络中的多种商品从不同的源节点运输到不同的汇节点的问题[13]，根据目标函数的不同主要分为最小化成本和最大化利润两类，且商品在流通中不能超过每条有向边（弧）的承载能力[14]。在传统多商品流模型基础之上，有序逃逸布线还需满足3 类布线约束，分别是线网非交叉约束、有序约束和容量约束[15]。

1.2 网络流建模

OER 问题是一类特殊的MMCF 问题。给定一个拓扑网络G=(V,E)，其中V代表的是所有节点的集合，E代表的是有向图中所有弧的集合。对于所有的节点，按照运输的目的分为供应节点、需求节点和中转节点3 类，其中：Vi代表逃逸引脚点的集合，对应MMCF 模型中的供应节点；Vt代表加入的假想节点，对应中转节点；Vb代表组件边界节点，对应需求节点。其中(i,j) ∈E代表从节点i到达节点j的有向弧。最终的网络流建模如图2所示。

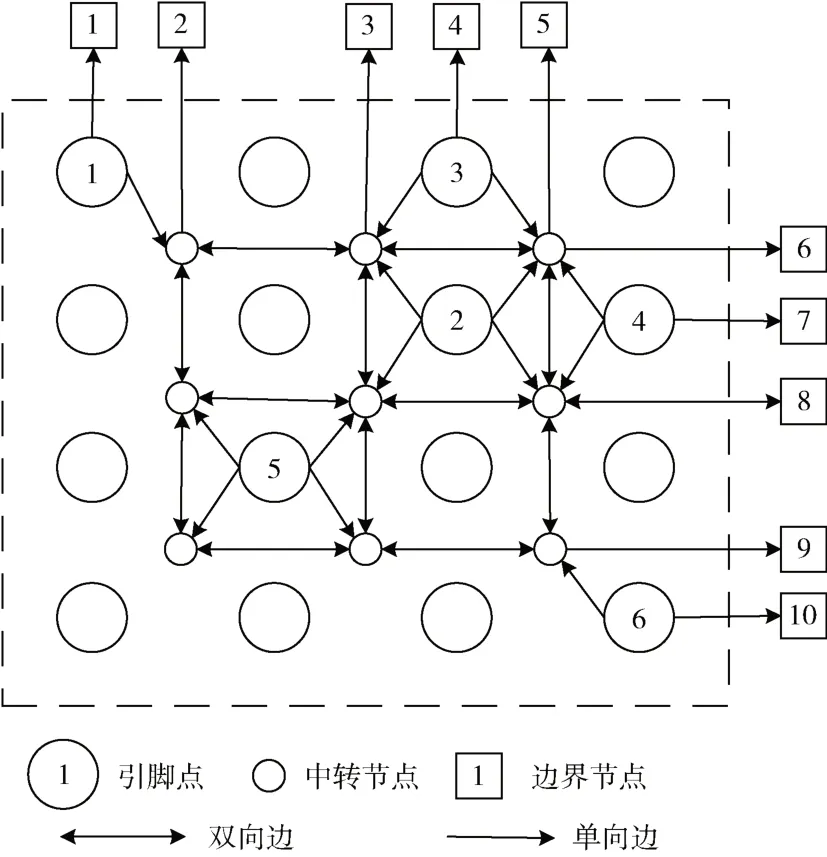
图2 网络流建模

为了便于描述问题，将其描述为整数线性规划约束式，引入以下符号：K表示所有待运输商品集合；表示弧段(i,j)上的最大运输量；表示第k个商品在节点i的需求量，>0 表示节点i是供应节点，<0 表示节点i是需求节点，=0 表示节点i是中转节点，每一个商品都需要从供应节点开始，经过一定的中转节点，最后到达需求节点；表示第k个商品在弧段(i,j)上的运输量；如果第k个商品在弧段(i,j)上有运输量，则=1，否则=0；表示第k个商品在弧段(i,j)上的成本。

目标函数：

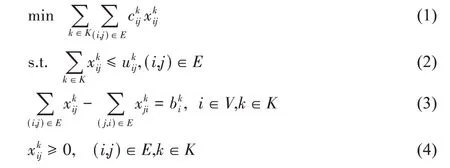
其中，目标函数（1）限制了每个弧段上所有商品的总流量；约束式（2）限制了每条弧段的容量；约束式（3）对3类节点分别作了约束，保证商品流在每个节点守恒；约束（4）为变量取值约束。

2 算法的设计与实现

一般来说，网络流问题通常采用启发式算法或者是整数线性规划求解。小规模的OER 问题可以采用整数线性规划求解，但处理大规模问题时，由于变量个数骤增，导致求解规模过大，无法直接求解。因此，本文采用线性化手段将其转化为线性规划问题，首先通过线性规划求解初始解，将其分解为多个逃逸路径，然后设计算法解决线网资源拥塞问题，最后迭代LP 从而得到最优解，算法主要流程如图3 所示。

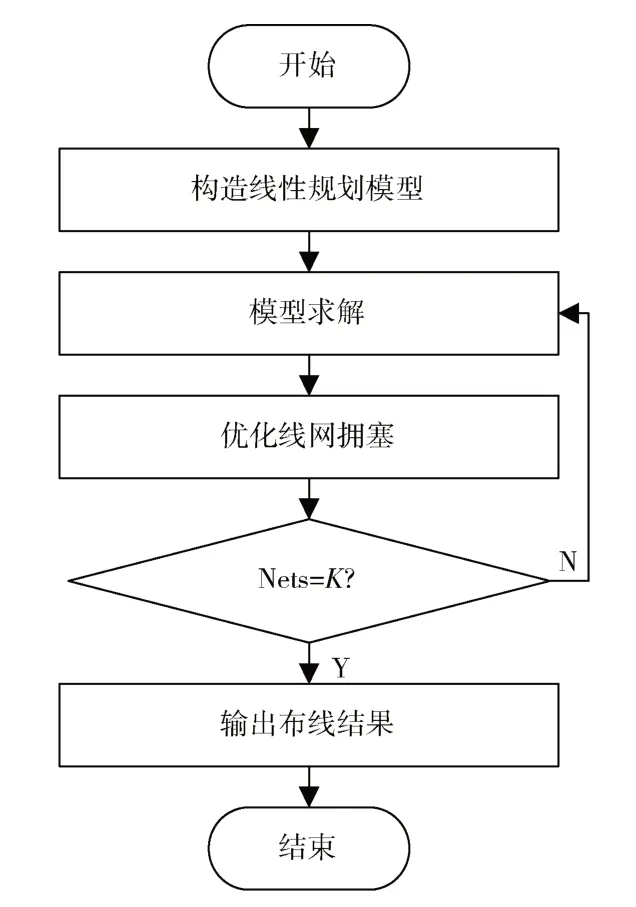
图3 算法流程图

LP 迭代算法的基本流程：

(1)对于每个逃逸引脚，构造其到边界节点的最短线长路径的线性规划式，从而形成初始逃逸方案，该方案可能存在多种逃逸路径，因为线性规划求解结果可能非整数。

(2)求解该线性规划模型，得到当前的最优解，并依照流值分配结果，生成逃逸路径。

(3)设计最大独立集算法求解所有路径结果是否为每个引脚根据主问题得到的路径结果。若路径数不满足逃逸引脚数目，则降低容量，返回步骤(2)；若满足，则进行步骤(4)。

(4)输出布线结果。

2.1 全局求解阶段

OER 问题主要考虑的因素除了容量和有序之外，还要考虑为了方便走线而加入的中转节点的交叉问题。记容量变量为，在LP 迭代过程中，其随着需求不断变化，直至满足可行解。

为了保证布通率的同时最小化线长，目标函数如下：

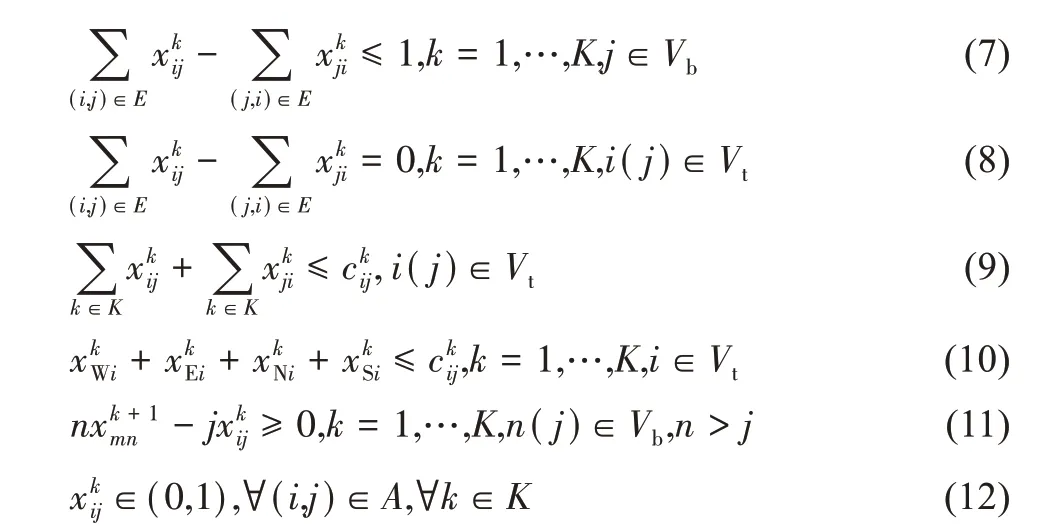
其中，ω是一个很大的常量。目标函数（5）是最小化线长和违反逃逸引脚数目yk的惩罚成本之和，只有当时，所得到的才是主问题的最优解；约束（6）为引脚点作为起始点的网络约束；约束（7）为边界点作为逃逸终点的网络约束；约束（8）为中转节点的流量守恒约束；约束（9）限制所有经过某中转节点的流值不超过其容量；约束（10）限制中转节点出现走线交叉情况，其中W、E、N、S 代表以i节点作为入点的4 个方向的有向边；约束（11）为有序约束；约束（12）为变量取值约束。

2.2 局部优化阶段

基于上述操作，得到了LP 初始解，但由于线性规划的解集为非整数，因此本次结果并不能作为最终的布线结果。根据LP 初始解的结果构造新的子图，使用深度优先搜索找到每个引脚对应的所有路径，将每条路径映射为路径点集。遍历所有路径线网，若不同引脚对应的线网之间存在交叉，表示有多个引脚重复占用局部线网资源，判定为拥塞区域，将这两个路径点对应相连，完成子图构建。

与传统增大拥塞区域权重来协商拥塞的方法不同，本文提出降低容量，迫使LP 求解时发散出更多的路径边，增加可选路的概率。为了得到具体的拥塞区域，采用最大独立集方法求解子图中的非交叉路径点集合，一方面得到当前部分引脚的逃逸路线，另一方面得到当前存在交叉拥塞的剩余路径集合。降低剩余路径中的容量并返回LP 模型，迭代求解，直至最大独立集求解出全部待逃逸引脚的逃逸路径，该路径集合则为主问题的最优解结构。

2.3 加速策略

对于大规模的OER 问题中引脚个数庞大，导致约束式规模骤增、求解速度缓慢、效率低下等问题，设计了相应的加速策略来提高迭代算法的求解效率。加速策略如下：

（1）利用启发式算法添加初始可行解

线性规划迭代求解算法需要不断根据局部优化阶段返回的拥塞结果调整区域容量，在求解过程中，LP 可能需要根据优化结果求解多次，如果重复重新建模并求解，则时间成本过大。采用Gurobi 支持利用启发式算法输入初始可行解的功能，可以提早确认部分引脚的逃逸结果，将其作为初始解输入到后期迭代模型中，这样既可以消除重复建模求解的时间消耗，还可以保存之前模型的最优解结构，加速Gurobi 的迭代求解。

（2）利用ILP 实现小规模分区求解

由于线性规划是全局求解函数，求解时间与变量规模成正相关，当迭代时间超过允许范围时，将线性规划作为分区条件，保留当前可行解。在未逃逸的引脚集合中，以当前引脚点为中心选定初始范围，并利用ILP 求解，若范围内未包含最优解，则向外扩散逃逸范围。经验证ILP 算法在小规模OER 问题求解已十分成熟，该策略大大缩减了不必要的迭代时间，加速主问题的求解。

3 实验结果

本节展示了所提出的基于线性规划的全局布线算法在有序逃逸布线方面的高效性。由于知识产权的限制，无法获得已发表的研究的执行代码，本文基本复现了MMCF 算法[12]来比较最终布线结果。由于设备差异和算法的实施具有随机性，本文复现的算法所得到的结果可能与原数据存在差异，但是对比文献[12]所给定的结果相差较小，因此将复现代码的结果作为本文算法结果的对比数据。另外，由于该问题缺少基准数据，因此在算法性能分析上除了采用从各类学术工作中收集的数据集(包括Case2、Case3、Case6、Case7、Case8）之外，为了更好对比算法在复杂绕障方面的性能，本文还随机生成了一些可布线的测试用例，共计10 组不同的测试用例。

本文算法采用C++语言在VS2019 平台上编程实现，线性模型采用Gurobi9.1 求解器优化求解[16]。算法在处理器为英特尔酷睿i7（主频为2.30 GHz）、内存为16 GB的PC 上运行。表1 所示为不同测试用例的布线结果。其中Col 和Row 表示引脚阵列的列数和行数，Pins 表示待逃逸引脚数量，Type 表示逃逸方向，本文默认引脚按顺时针方向逃逸。图4 给出了Case10 的布线结果。

表1 全局逃逸布线算法结果对比

图4 Case10 最终布线结果

在小规模引脚阵列情况下，本文算法与MMCF[12]运行性能相差不大，二者都可以在合理的CPU 时间内保持高布通率。随着引脚阵列规模和PCB 复杂程度增大，MMCF 方法[12]的时间复杂度增长很快，在Case9 中，两种算法都能实现100%的布通率，但是本文算法相较于MMCF 算法，CPU 时间平均优化50%，线长优化平均提升31%。当处理大规模引脚阵列如Case10 时，MMCF 求解器在求解过程出现CPU 运行时间违规，布线失败。而本文算法不仅能够逃逸出全部的引脚，而且能够实现线长和运行时间的双重优化。

4 结论

本文提出采用线性规划方法作为全局求解器求解有序逃逸布线问题，建立了相应的求解约束式，通过流分解成路之后采用最大独立集方式优化拥塞，为求解大规模的此类问题提供了一种新的方法。测试结果表明，所设计的基于线性规划的迭代算法在解决大规模或者是引脚阵列密集的有序逃逸布线问题时有很大的潜力。后续的研究可以在多商品流问题中考虑更多的加速策略，如优化求解方式等。