K-means 聚类-DCT 压缩算法在振动传感器中的研究与应用*

王昱钦，王 鑫，刘保强，李 轶，洪 晟

（1.江苏自动化研究所，江苏 连云港 222000；2.中国人民解放军32381 部队，北京 100000；3.北京航空航天大学 网络空间安全学院，北京 100191）

0 引言

在工作时机械设备基本都存在比较明显的振动情况，如果想要监测设备的运行状态，是可以通过分析机械设备所产生的振动信号来实现的，并且通过分析监测结果的变化情况可以在早期及时地发现机械设备可能出现的故障情况[1]。但是如果要想通过设备所产生的振动信号对其运行状态情况获得非常准确的评估或预测结果，则需要对机械设备所产生的大量高频振动数据进行有效分析[2]，为了能够有效采集到大量高频振动数据，需要安装大量的传感器用于采集机械设备在工作时所产生的高频振动数据[3]。但是现有的基于ZigBee、蓝牙技术等低功耗、低速率的无线传输技术是无法满足此类应用需求的，无法满足需求的原因主要有两个方面[4]:(1)对高频振动数据进行采集会快速消耗终端节点所使用的电池电量，进而影响整个采集系统的工作寿命；(2)大量数据的无线传输会严重占用系统带宽资源，从而会造成传输过程丢包率的升高，最终会影响到数据分析的准确性[5]。

对数据进行压缩的主要目的就是想要通过传感器在边缘侧的运算，较大幅度地减少数据在无线传输过程中所消耗的能耗，虽然这样会损失传感器的部分能耗[6]，但只要确保传感器所消耗的这部分能耗要大大低于传输过程所需能耗，就可以实现总能耗的减少，但并不是所有的数据压缩算法都可以达到这一目的的[1]。针对上述问题，本文首先对现有多种振动数据压缩算法进行了研究，对现有压缩算法存在的问题进行了分析，并在此基础上提出了一种面向无线通信的数据压缩算法——K-means 聚类-DCT 双重压缩算法。通过实际验证表明，采用该算法对振动数据进行数据聚合，可以非常明显地提高数据压缩的效率，从而在传输时将冗余数据有效减少[7]。而在相同数据量情况下，采用改进算法的峰值信噪比与其他算法相比，具有更好的性能。

1 振动数据压缩研究概述

设备预测性维护是通过采集机械设备运行时所产生的振动数据，然后对振动数据进行分析，通过分析所采集到振动数据并根据分析结果来确认机械设备的运行状态是否正常。奈奎斯特采样定理指出，如果需要对模拟数字信号进行转换，在其转换的过程当中，如果采样频率是所采样信号中最高频率的2 倍及以上时，完成采样后所得到的数字信号就能够将原始信号中的全部信息完整地保留下来[8]。机械设备可能在特定情况下产生高频振动，为防止振动数据在采样后频域出现混叠情况，在对振动数据进行采样时，有必要采用较高的采样频率。这造成了传感器将采集大量的振动数据，由于无线传感器对于功耗的要求，将大量数据直接上传至采集基站无疑将大大降低无线传感器的实际使用寿命。为有效延长传感器实际使用寿命，在确保较高采样频率的前提下，通常会应用数据压缩算法对传感器采集到的振动数据进行压缩，从而能够将传感器传输数据的效率大幅提高，并且可以将数据传输的时间大大降低，最终大幅降低传感器的实际功耗。通过压缩算法来提高数据传输效率是振动监测领域通用做法[9]。

无线传感器所采用的压缩算法可分为无损压缩算法和有损压缩算法。其中无损压缩算法是指接收到被压缩的数据后能够将压缩后的数据完整恢复的算法，最为典型的无损压缩算法有LZW 压缩算法、Huffman编码、行程编码方法等[10]。LZW 压缩算法是一种基于字符字典库的无损压缩算法，该算法通过建立一个字符字典库，用一个数字来代表放入字符字典库中的第一次出现的字符串，如果这个字符串再次出现时，即可用表示它的数字来代替，然后使用较短长度编码来对较长的字符串进行标识，通过这样的方法来最终实现对数据的压缩[11]；Huffman 编码是一种用于无损压缩的熵编码算法，该算法首先会统计出需要压缩的数据当中所有字符出现的概率，然后在对数据进行重构的过程中是按照字符出现概率的高低进行的，使用较短的编码字符来代替所有出现概率高的字符，最终将整体数据量压缩到最小[12]；行程编码方法也叫RLE 压缩编码，是Golomb 于1966 年提出的一种相对简单的编码技术，其原理是将由相同数值组成的连续数值串通过数值串的长度以及代表数值来表示，从而使得压缩后的数据量要小于初始的数据量[13]。目前有损压缩算法主要都是对现有算法的改进或者裁剪，其中比较典型的有损压缩算法主要有小波变换方法、时间顺序近似方法等。

对于预测性维护，在满足系统要求的前提下，可对振动数据进行有损压缩。Liu 和Cheng[14]提出了一种应用于设备状态监测的传感器数据压缩方法，方法是用DWT 和DSC 实现对振动数据的压缩处理。Steffen 等人在文献[15]中提出了一种传感器的自适应压缩算法，该方案对传感器性能要求非常高，而传感器往往出于节能考虑，采用的控制处理器性能都比较低，复杂的压缩算法增加了传感器的处理时间，导致数据无法及时发送[16]。Yoon[17]提出了一种基于无线传感器网络自适应压缩率的选择方案，该方案可以根据电池的电量状况来选择不同的压缩模式，在电池电量充足时，自适应选择使用高性能的压缩方案；反之，在电池电量较低时，则自适应选择计算量相对较低的压缩方案，通过该方式实现能量使用的均衡。在文献[18]中，作者提出基于近似多项式的数据压缩算法，并将其应用于非周期信号测量中。在文献[19]中，作者提出了一种应用于无线传感器网络数据传输的压缩效率较高的无损压缩算法，该算法的核心采用了LZW 算法[11]，实际由于LZW 算法较复杂，对于传感器硬件压力过大，且对RAM 要求过高，使用该算法将极大地影响传感器功耗，由于LZW 算法为通用压缩算法，实际用于传感器数据压缩性能提高有限。

但是大部分的以上工作并不适用于机械振动的振动数据压缩，由于算法复杂度以及低功耗无线传感器的资源限制，其中有些算法不适用于此类应用场景。鉴于此，本文着重针对机械振动数据的监测，提出了一种新的高效数据压缩算法，在重复考虑算法复杂度和计算复杂度的同时，对振动数据处理有着更高的压缩效率，适用于预测性维护的应用场景。

2 K-means 聚类-DCT 双重压缩算法研究

没有一种压缩算法能适用于各种传感器数据的压缩，例如振动旋转电机的振动数据压缩算法，用于往返振动所采集的信号时，可能性能也存在问题。因此，算法需要针对所监测对象进行设计。机械振动信号在时域变换较快，但是在频域表现为重叠和噪声[20]。Kmeans 聚类-DCT 双重压缩算法针对预测性维护数据特点，本文首先利用K-means 算法对振动数据进行聚合分类，再根据振动信号频域特点进行离散余弦变换(Dis‐cret Cosine Transform,DCT)压缩。压缩流程如图1所示。

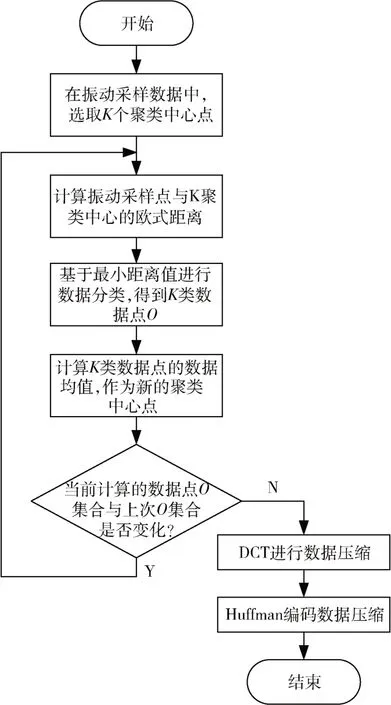
图1 数据压缩流程

针对振动数据特点对ADC 所采集到的数据进行初步类，主要步骤如下：

(1)将ADC 采集的振动数据D={x1，x2，…，xn}，任取k个数作为聚类中心，用M={m1，m2，…，mk}表示。

(2)算出N={n1，n2，…，nm}与聚类中心M之间的欧式距离，N∈D且N∉M。

(3) 比较距离值，依据d(mi,ni)=min{d(m1,ni),d(m2,ni),…,d(mk,ni)}，将振动数据D根据最小距离划分为k类O={o1，o2,…,ok}。

(4) 重新计算O中数据均值，作为新的中心M∗，重复步骤(1)～(3)。将数据重新归类为新的k类

(5) 比较O与O*中数据情况，如果数据依然存在变化，重复步骤(4)，直到每类中数据对象在误差平方和函数收敛时，停止迭代。

对振动信号进行FFT 能直观地反映信号的频域特点，振动信号可能包含多个高频域振动信号，或是分布在宽频的随机信号构成。振动信号在基于K-means 聚类算法处理后，利用离散余弦变换的变换域压缩，去除信号的相关性，减少冗余数据。由于小波变换具有良好的时域定位和能量集中特性，对归类后的振动信号f(x)进行DCT 变换，用下列公式表示：

其中，k(m,x)为DCT 变换的变换核。

将振动数据变换到频域后，对变换后的数据进行量化，并采用Huffman 编码对变换后的数据进行二次数据压缩。

3 实验数据分析

无线振动传感器硬件基于STMicroelectronics 公司低功耗单片机STM32l476 实现，振动MEMS 芯片采用ADI 公司ADXL1002，线性度为±0.1%，量程为±50 g。采样频率20 kHz，采用ADI 公司ADS8689 16 位ADC。采用K-means 聚类-DCT 双重压缩算法，与标准DCT、DWT、LZO 编码进行压缩对比。

STM32l476 MCU 一款基于高性能的Arm® Cortex®-M4 32 位内核，最大工作频率为为80 MHz。考虑到采集的振动数据量，传感器采用UWB 模块实现无线通信，将数据采集数据通过UWB 模块发送至实验计算机，再使用仿真工具对数据进行处理。测试环境由SD&PTI PE 型通用振动台功放设备及泰克AFG1062 任意波形函数信号发生器构成，AFG1062 生成正弦振荡波形，经由功放设备放大，驱动振动台振动。传感器硬件如图2 所示。在真实测试环境中，传感器采用磁吸方式吸附在传动机构电机的轴向位置，与电机轴水平位置垂直，并采用粘胶固定。

图2 传感器硬件图

3.1 算法效果评估指标

为评估算法效果，文中使用压缩率衡量算法压缩情况，压缩率定义如式(1)所示:

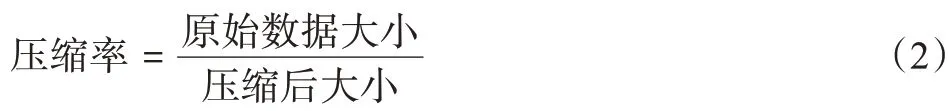
由于DCT 是有损压缩方式，本文用峰值信噪比（Peak Signal to Noise Ratio,PSNR）来评估压缩质量，计算公式如式(2)、式(3)所示。

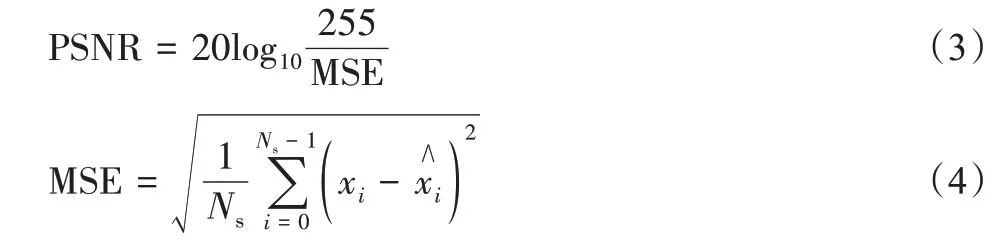
其中，Ns为总采样数据量，为压缩后的振动数据。

3.2 数据分析

实验分别采集1 k、2 k、4 k、16 k 个点，每个点为16 bit浮点数，每次采集10 次，使用MATLAB 进程处理，并对每种算法的实验结果进行均值处理，结果如表1 所示。

表1 实验数据表

从图3 和图4 的实验结果看，采用K-means 算法对振动数据进行数据聚合，可以非常明显地提高数据压缩的效率，从而在传输时将冗余数据有效减少。而在相同数据量情况下，改进算法在峰值信噪比方面与其他算法相比具有更好的性能。

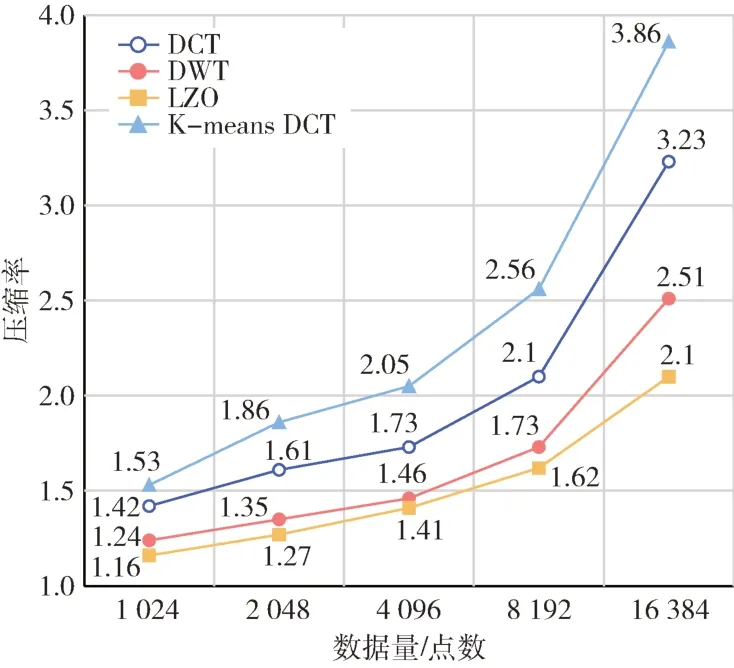
图3 压缩率曲线

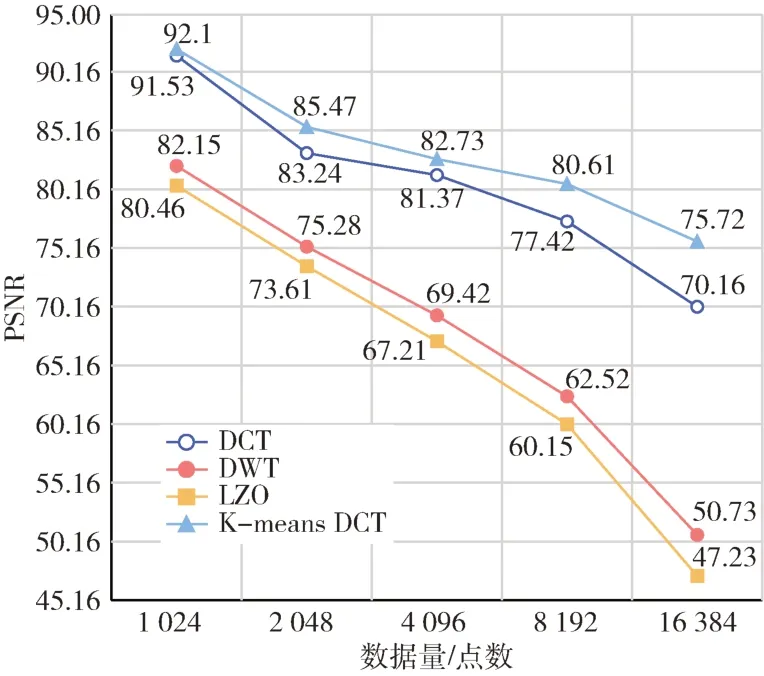
图4 PSNR 曲线

4 结论

本文针对预测性维护振动数据的特点，对DCT 算法进行了针对性的改进，并且通过K-means 聚类算法对振动数据进行了进一步处理，根据数据特性将数据进行了相应分类，从而可以更好地利用DCT 算法的压缩性能。通过对实验数据的处理分析，与DCT、DWT、LZO 算法进行对比，双重压缩算法在压缩率和峰值信噪比上具有更好的性能。