基于时差法的双声道超声波水流量计

刘 伟，秦会斌

（杭州电子科技大学 新型电子器件与应用研究所，浙江 杭州 310018）

0 引言

流量检测是工业自动化检测中的一个重要指标，与温度、压力并称为热工计量的三大重要参数[1]。流量计作为流量检测的标准计量器具，在于流体相关的工业控制中起到重要作用。传统的流量计大多为机械式流量计，机械部件占据主体部分，流体流经流量计时，流量计借助机械部件的转动完成流量计量。因此，机械式流量计普遍存在始动流量高、压力损耗大、需要人工抄表的问题。随着超声波检测技术的发展，出现了利用超声波完成流量测量的超声波水流量计。超声波流量计内部采用全电子结构，无阻流部件，相较于传统机械式流量计具有非接触式、无机械化部件、测量灵敏度高、受环境影响较小等优点[2]。因此，基于超声波检测技术的流量计逐渐成为热门研究领域。研究人员从超声波测量原理、传播时间计算方法和流量计设计等各个方面开展研究。涂晓立等人采用多普勒法研制了一种超声波多普勒流量计，并对流量计的性能进行了测试[3]；王安然等人对超声时差法的传播时间测量进行分析，提出了一种基于电容积分的间接传播时间测量方法[4]；胡海霞采用高精度计时芯片TDC-GP22 设计了一款运用于小口径管道的超声波计量模块[5]。

这些研究为超声波水流量测量领域的发展起到了重要作用。但是，现有的中小管径超声波流量计设计大都采用单声道，少有采用双声道或者多声道，而由于管道内存在气泡、颗粒物等杂质，流场分布不均匀等因素的影响，单声道流量计测得的流速并不能充分反映管道流体流速，而多声道流量计通过测量每个声道的线速度，并通过数据融合的方式将多个线速度进行融合，融合结果作为管道内的流体流速，因此测量精度更高[6−7]。为了进一步提高超声波流量计的精度和稳定性，本文设计了一种基于时差法的双声道小管径超声波流量计。此外，如何将多个单声道流量计的测量结果融合，直接影响到了双声道流量计的性能。对此，本文提出了一种基于卡尔曼滤波算法的数据融合方法，有效地降低了外部噪声的干扰，提高了流量计的测量精度。

1 系统工作原理

1.1 时差法测量流量原理

超声波流量计测管道流体流量的工作原理是时差法。超声波在顺流传播状态下，超声波声速和流体流速叠加，导致超声波传播时间减少。在逆流传播状态下，超声波传播速度与流体速度相抵，造成超声波传播速度下降，进而使传播时间增加。通过测量超声波顺逆流传播时间差可以间接计算出流量大小，其具体的计算方式如下文所示，超声波流量计时差法测量原理图如图1所示。

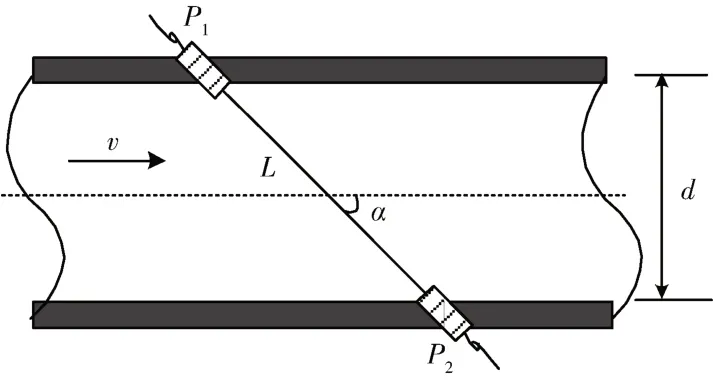
图1 超声波时差法流量测量原理图

图1 中，P1、P2为两个收发式两用超声波换能器，两换能器之间的距离为L，管道直径为d，水的正向流速为ν，换能器之间连线与管道中心线之间的夹角为α。通过换能器P1和P2交替发射和接收超声波，可测得超声波顺流传播时间和逆流传播时间的时间差[8]：

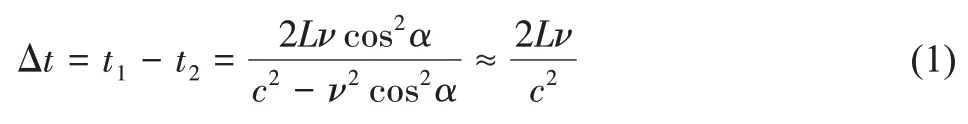
由于超声波传播速度c远远大于水流速ν，因此式（1）中ν2可以忽略不计。由式（1）可得水流速ν：

已知管径为d，则管道水体的累计水流量为Q：

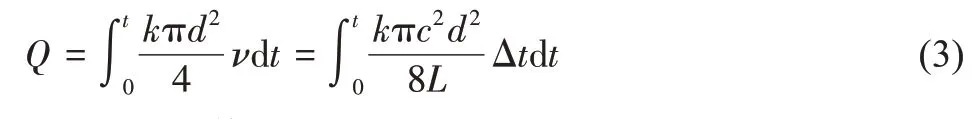
式中：k为流速修正系数。

1.2 基于卡尔曼滤波的双声道数据融合方法

在超声波流量测量过程中，由于外部环境噪声的干扰与系统内部结构的限制，如环境设备振动、工频干扰、流体扰动等[9]，使得超声波信号在传播过程中被掺杂大量噪声，测量结果与实际流量值存在误差，影响流量计的测量精度。因此，为了提高超声波测量信号的信噪比，需要对测得的时差数据进行滤波处理。为了同时对多个声道的测量结果进行滤波处理，本文设计了一种基于卡尔曼滤波的数据融合方法来处理两个单声道流量计的测量结果。

1.2.1 双声道数据融合方法

数据融合方法建立在双声道布置结构上，双声道交叉布置结构如图2 所示。对双声道交叉布置方式进行拆分，可以看作是两个单声道超声波流量计，换能器1、2组成单声道超声波流量计A 的一对换能器；换能器3、4组成单声道超声波流量计B 的一对换能器，从管道侧面看，两个换能器对正交分布。

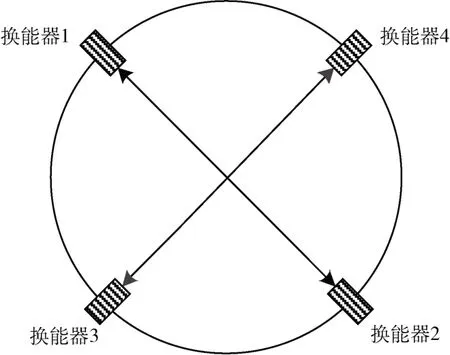
图2 双声道超声波流量计声道布置结构侧面图

管道内流场的分布情况较为复杂，需要根据管道内的流场分布情况，分别计算出两个单声道流量计所在声道的测量结果在卡尔曼滤波融合方法中的权重系数，即流速修正系数。假设管道半径为R，距离管道中心轴线距离为r的流体流速为ν(r)。对速度ν(r)关于横截面积S进行积分，求得面平均速度。

对某个单声道超声波流量计换能器对连线上的线速度ν(r)进行积分，求得线平均速度:

式中：L为测量单元两换能器的距离，dl为L的微元，i为声道数。

根据式(4)和式(5)可求得第i个声道的权重系数ki。

根据式(6)计算出声道权重系数k1和k2之后，对两个单声道流量计的测量结果进行卡尔曼滤波融合计算。

则最终水流量的计算公式修正为：

1.2.2 卡尔曼滤波融合计算

卡尔曼滤波分为预测和修正两个步骤，其计算逻辑是：先用上一时刻最优估计值预估当前状态，再根据预估值来修正当前测量值，其具体迭代过程如下：

计算上一时刻的输出结果来预测当前状态:

式中：A和B是系统参数，液位稳定时为单位矩阵，Δt'Last是上一采样点的最优预测值，ULast为上一采样点的系统控制量。

由于测量值、真实值和噪声的协方差都符合高斯分布，因此当前测量协方差定义为：

式中：Plast为上一个采样点的预估协方差，本文设定初始采样点的Plast和PNow是相等的，q为过程噪声的协方差。

当前时刻的卡尔曼增益Kg为：

式中：R为观测噪声的协方差。

当前传播时间差输出结果ΔtNow可由当前两个声道的测量值Δt1、Δt2和上一个输出结果ΔtLast计算得出：

式中：ΔtNow即为卡尔曼滤波的输出结果Δto。

计算下一个采样点的预估协方差：

2 系统硬件电路设计

双声道超声波流量计的系统硬件结构图如图3 所示。系统采用低功耗单片机STM32L431 为主控芯片，单片机主要负责控制声道切换电路完成声道切换，驱动TDC-GP22 模块和LCD 屏，完成对测量数据的处理和计算。TDC-GP22 模块为高精度计时芯片，在单片机的驱动下发射和接收超声波，完成超声波传播时间的测量。电源模块提供3.3 V 电压供电单片机，通过稳压芯片AMS1117 输出3.0 V 电压为计时芯片供电。

图3 超声波流量计硬件结构图

2.1 TDC-GP22 计时模块

本系统采用TDC-GP22 高精度时间数字转换芯片完成传播时间差的测量。该模块内部集成了温度测量电路、TDC 测量电路、时钟控制电路、高速脉冲信号发生电路[10]。计时芯片的FIRE_UP 和FIRE_DOWN 端口分别和两个超声波换能器相连。XIN 和XOUT 两个端口连接在4 MHz 晶振电路上，用于内部时钟校准。TDCGP22 通过SPI 通信与单片机进行信息交互。INTN 端与单片机的IO 口相连，当达到了预设的采样数或者测量溢出，该端口为低电平。CLK32OUT 和CLK32IN 端口为32 kHz 晶振端口，其用于校准温漂较大的4 MHz 高频陶瓷晶振。模块电路原理图如图4 所示。

图4 TDC-GP22 硬件电路

2.2 声道切换电路

系统选用双四通道模拟开关CD4052 实现声道切换，其中每个声道都是独立的输入/输出通道，由于系统采用的是双声道布置结构，因此只需要使用其中的两个声道。CD4052 具有较低的导通阻抗和截止电流，通过信号的幅值最高可达20 V，完全符合设计要求。

3 软件设计

系统软件设计完成包括单片机的初始化、LCD 屏的驱动、设置采样频率等，主要实现对TDC-GP22 模块和声道切换电路的控制，完成水流量的测量，并将测量结果显示在LCD 屏上。主程序流程图如图5 所示。

图5 系统主流程图

时间测量程序流程图如图6 所示。

图6 时间差测量程序流程图

系统上电后，单片机先发送指令0x50 给TDC-GP22芯片上电；然后发送指令0x03，计时芯片会根据晶振电路完成时钟校准，发送0x07 初始化计时芯片的相关寄存器配置，包括芯片开启第一波检测模式、选择测量模式2等；发送指令0x05 开启两次时间间隔的测量；之后等待芯片内部产生START 信号，接收到信号后计时开始；当STOP 端接收到预置的采样数或者测量溢出，计时单元停止计时；测量结束，中断端口INTN 被置0，单片机可以通过循环检测INTN 端状态判断测量是否完成；发送指令0xB3 读取结果寄存器结果，完成上游时间间隔的测量。再次初始化计时芯片，以便可以接收新的START和STOP 信号，等待START 信号，开启下游时间间隔的测量。完成两次时间间隔的测量，即可计算出传播时间差。传播时间差通过卡尔曼融合滤波算法滤除噪声获得更精准的时间差数据，根据时间差数据采用时差法即可计算出水流速和水流量[11−12]。

4 测试与分析

4.1 测试方案与结果

实验中，将设计的双声道超声波流量计样机和标准流量计安装在同一管段上，标准流量计采用精度等级为0.5 级、测量范围为0.1～15 m/s 的电磁流量计，通过阀门调节流量大小，根据标准流量计示数调节流量大小，分别读取样机和标准流量计的流量数据。实验管径为DN50，实验的测试范围为0.1 m3/h～31.25 m3/h，设置8 个流量点。每个流量点测量6 次，取平均值作为测量值，并计算每个流量点的测量数据与标准流量计之间的相对误差。

表1 为实验样机与标准流量计测得的流量数据对比，示出了8 个流量点的累计流量数据。从数据对比结果可以看出，在管道流量较小的情况下，样机和标准流量计的测量值相对误差较大，随着流量的增大，相对误差减小，从总体上看相对误差控制在2.5%以内。

表1 数据对比

4.2 算法效果分析

为验证卡尔曼融合滤波算法的滤波效果，随机选取某流量点进行测试，验证实验一共测量100 组时差数据。单声道流量计A 在该流量点测得的顺逆流传播时间差Δt1如图7 所示；同理，单声道流量计B 测得另一组顺逆流传播时间差Δt2如图8 所示；然后，采用卡尔曼融合滤波算法对数据进行融合滤波，得到的滤波结果如图9 所示。

图7 Δt1 的时差数据

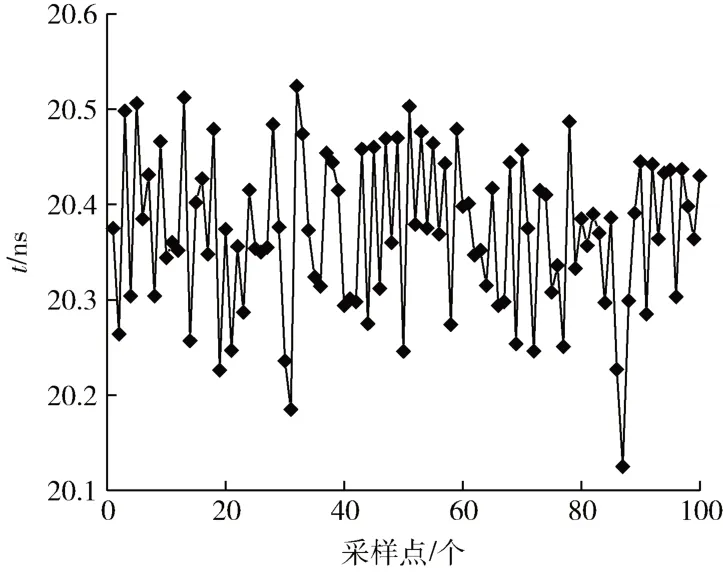
图8 Δt2 的时差数据

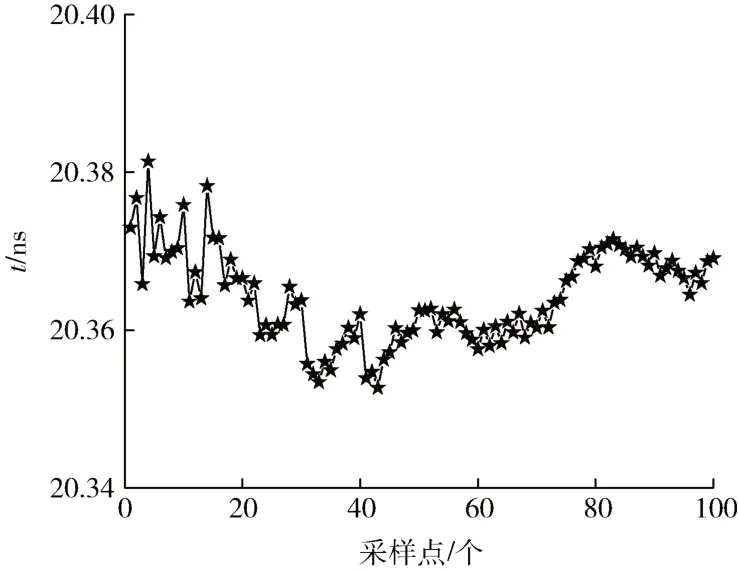
图9 滤波后的时差数据

从图7～图9 可以看出，两个单声道流量计的时间差输出波动较大，而经过双声道卡尔曼融合滤波之后，波动明显下降。由此可见经过双声道卡尔曼滤波处理后，超声波流量计具有更高的精度和更好的稳定性。

对该流量点，计算两个单声道流量计输出结果的标准差和双声道卡尔曼融合滤波输出结果的标准差，标准差std(Δt)的计算方式如下：

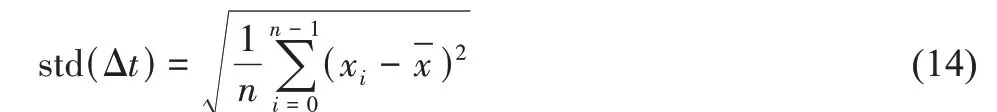
5 结论

本文设计了一种基于时差法的双声道超声波流量计。采用高精度时间计数芯片TDC-GP22 完成对超声波顺逆流传播时间差的测量，并采用时差法计算对应的水流量；根据双声道布置结构提出了一种基于卡尔曼滤波的融合滤波算法，提高了流量计的测量精度。测试结果表明，流量计流量测量相对误差在2.5%以内，符合超声波流量计的行业标准，对工业流量测量领域的发展具有一定的现实意义。