基于EEMD-PSO-ELM的RV减速器故障诊断模型
刘永明,叶国文,赵转哲+,张 振
(1.安徽工程大学 机械工程学院,安徽 芜湖 241000;2.安徽工程大学 人机自然交互和高效协同技术研究中心安徽省新型研发机构,安徽 芜湖 241000)
0 引言
旋转矢量(Rotate Vector, RV)减速器是一种新型的摆线针轮行星传动的二级减速器,目前主要应用在机器人领域和航空领域。随着工业机器人的需求日益增加,作为机器人核心部件,形成鲜明对比的是RV减速器的可靠性问题,亟需一种关于RV减速器的故障诊断和寿命预测平台来降低由于RV减速器故障带来的损失。
近年来,学者们对于减速器做了大量研究,潘柏松等[1]在考虑齿轮磨损的情况下对行星齿轮减速器做了传动精度的可靠性分析;AN等[2]提出一种使用声发射(Acoustic Emission, AE)测量的基于隐马尔可夫模型(Hidden Markov Model, HMM)的RV减速器故障检测。CHEN等[3]提出一种基于非线性输出频率响应函数(Nonlinear Output Frequency Response Fuctions, NOFRFs)和深度卷积神经网络(Convolutional Neural Network, CNN)的RV减速器故障诊断新方法。为了识别RV减速器在不同工况下的故障,PENG等[4]提出一种噪声深度卷积神经网络(Noise deep Convolution Neural Network, NOSCNN)模型。YANG等[5]提出一种二维卷积神经网络(2D-CNN)用于安装在工业机器人(Industrial Robot, IR)上的RV减速器的故障诊断。ROHAN等[6]提出使用控制单元(Motor Current Signature Analysis, MCSA)的嵌入式电流信号作为检测和诊断机械故障的方法,并将其应用到RV减速器上。GUO等[7]提出一种带有基于水平的学习群优化器(Level-based Learning Swarm Optimizer with Extreme Learning Machine, LLSO-ELM)的极限学习机,用于工业机器人RV减速器的故障诊断。WANG等[8]利用RV减速器刚度波动机理实现对RV减速器缺陷部位的快速诊断,具有很强的工程应用价值。李哲等[9]采用在多个位置放置传感器进行数据提取,并进行预处理,进行初步处理,将解析出的信息引入到深度卷积神经元网络中,改善了现有针对减速器故障诊断的准确性和鲁棒性;王久根等[10]将振动试验台测得的不同故障模式数据输入残差神经网络进行训练和5折交叉验证,并与多个神经网络模型比较,同时采用西储大学数据库验证;毛君等[11]将减速器常见的几种故障特征作为输入,有无故障作为输出;彭鹏等[12]明确提出了噪声影响下的卷积神经元网络实体模型,将RV减速器的一维振动数据信号二维化后转变成灰度图像,将其作为输入并融合了特征;陈乐瑞等[13]根据离散系统的输出相位频率特征函数和核主成分分析(Kernel Principle Component Analysis, KPCA),选择了一种紧密结合频带的方法,并选择了大量可能的优化算法,得到前4个频带值在每种情况下,使用KPCA解决方案后,引入支持向量机(Support Vector Machine, SVM),并与多种诊断方法进行比较。安海博等[14]分析了RV减速器动力学的基本原理,建立了RV减速器内部声发射数据信号的传播模型;于宁等[15]对故障信号进行组合模态函数(Combined Mode Function, CMF)分解,改进局部均值分解(Complementary Ensemble Local Mean Decomposition, CELMD),结合多尺度排列熵法(Multiscale Permutation Entropy, MPE)选取乘积函数(Product Function, PF)分量进行重构和包络分析等综合诊断方法。QIAN等[16]提出一种使用克里金模型的具有多种故障模式的工业机器人RV减速器的时变可靠性方法。上述针对RV减速器的故障诊断方法精度较高,但方法内容较复杂,复杂计算较多,同时需要大量的数据支撑,往往RV减速器在产生初期故障的时候数据特征较少,而且大多数故障诊断的特征均从时域和频域入手,选择旋转周期作为故障特征较少。
随着人工智能发展,极限学习机由于其运行速度快,训练数据量少,作为一种模式识别得到了重视,WANG等[17]采用极限学习机方法对燃油系统的故障进行分类。GUO等[18]将圆模型和极限学习机(Extereme Learning Machine, ELM)相结合,形成一种线性模拟电路的故障诊断方法。XIA等[19]报告了一种结合核熵分量分析(Kernel Entropy Component Analysis, KECA)和基于投票的ELM(Voting based ELM, VELM)的冷水机组早期故障的有效诊断方法。LI等[20]提出一种基于极限学习机和AdaBoost. SAMME的核电站故障诊断框架。LIU等[21]提出了一种使用有限元法(Finite Element Method, FEM)仿真和ELM的个性化故障诊断方法来检测齿轮中的故障。上述研究通过各种方法与极限学习机结合进行故障诊断,取得了较好的结果,但大多普适性较差,而且由于ELM的权值和阈值具有随机性,每次出的结果并不稳定,容易影响预测结果。
对此,本文提出一种基于集成经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)的小样本工业机器人RV减速器PSO-ELM故障诊断分类模型。每个旋转机械受加工精度和装配精度等因素影响,在运行时都会或多或少地偏离轴心,假设偏离的距离为h,h=Asin(ωθ+γ),式中:A表示旋转时偏移轴心的最大距离;ω表示旋转时的周期频率,γ表示旋转时的初始相位角。随着旋转机械使用时间的增长,在摩擦磨损作用下,其偏离的距离h会随着使用时间的增长而变大和变得不规律,继而产生断裂等故障。由于故障的位置不同,h也会产生不同的变化,而导致h变化的原因为wθ+γ发生变化,其中ω变化在旋转机械中可通过分析测得数据的周期性得知。
由于RV减速器产生的故障特征并不明显,造成了RV减速器在运行时的精度降低而无法发觉,基于旋转机械ω变化可通过分析测得数据的周期性的思想,本文提出一种基于EEMD-PSO-ELM的故障诊断模型。其中,EEMD可以很好地反应出数据在故障时的瞬时频率,在故障数据信息较少的情况下,从瞬时频率中反映出的周期性可以提高RV减速器故障诊断的准确率,进行合理的故障检测。
1 工业机器人RV减速器
1.1 工业机器人RV减速机结构
如图1所示,RV减速器由太阳轮作为输入轴,由少齿数的太阳轮带动多齿数、大一点的行星轮转动进行一级减速;大行星轮推动曲柄轴旋转,曲柄轴带动2个RV轮旋转,两个RV轮转动一圈,针齿轮转动一齿,进行二级减速。
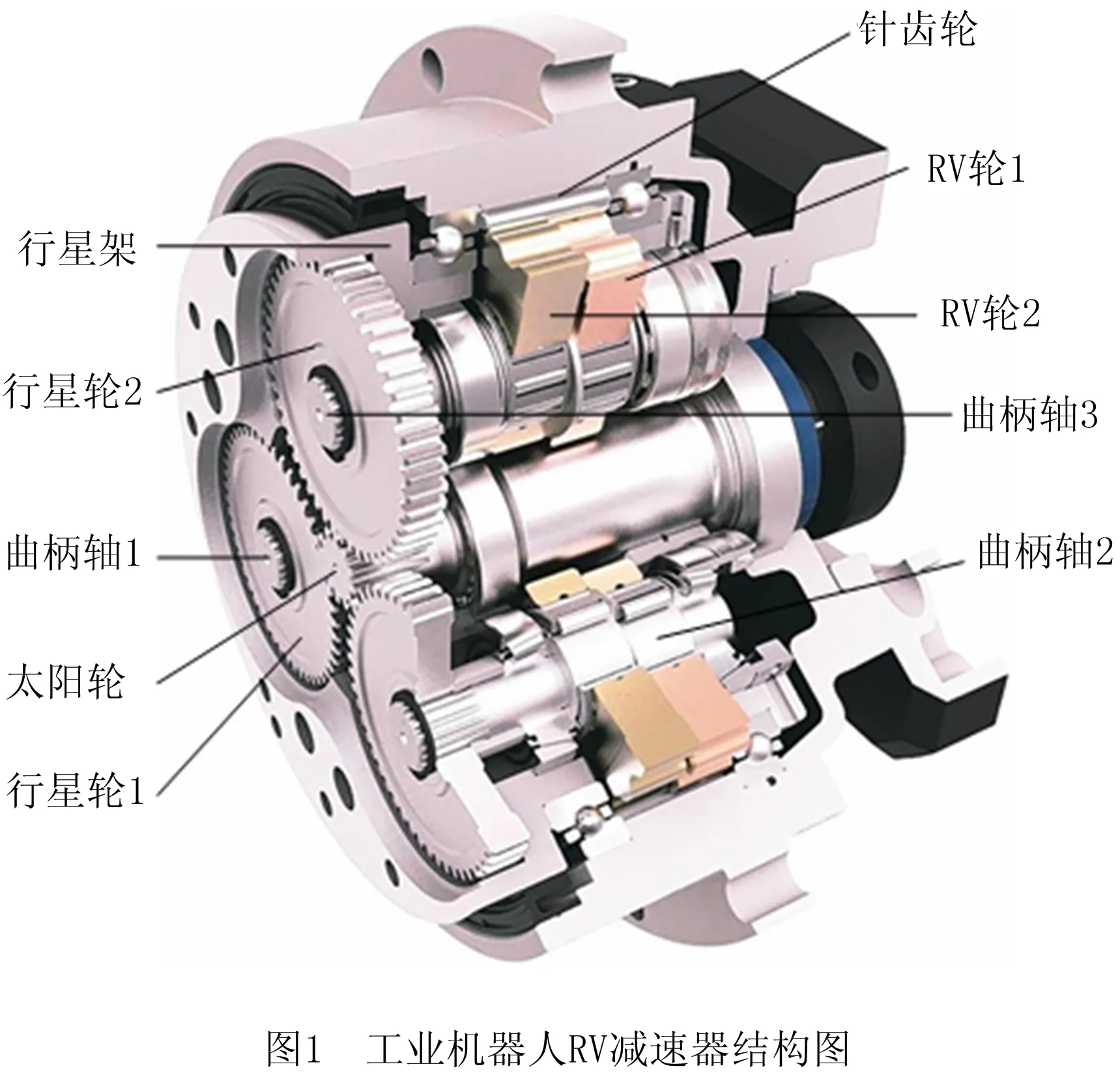
曲柄轴由于其重心不在轴心上,其扭矩会随着转动呈周期性变化,计算公式如式(1)所示[22]:
(1)
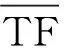
(2)
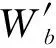
由于RV减速器曲柄轴不需要曲柄平衡块,对于RV减速器式子可以表示为:
(3)
扭矩因数可以表示为:
(4)
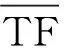
(5)
而摆线轮的中心与轴心不在一条线上,假设其差值为s,摆线轮的半径为r,则摆线轮的公式为:
(6)
摆线轮与针齿轮传递扭矩时,其扭矩需要添加一个啮合系数c1。则其最终的输出扭矩为:
(7)
由于效率公式为:
(8)
式中n表示减速比,则由式(8)可以得出正常运行RV减速器的效率具有周期性。
2 EEMD-PSO-ELM模型的建立
2.1 EEMD预处理
经验模式分解(Empirical Mode Decomposition, EMD)是一种可以反映出数据瞬时频率的分解方法,但由于加入的噪声为随机产生,容易导致模态混叠、端点效应、筛分迭代停止标准等问题。针对上述问题,WU等[23]提出了集成经验模式分解(EEMD)。该方法通过加入白噪声填补非连续信号段信号解决模态混叠现象。在噪声信号分解的过程中,运用白噪声信号的滤波特性,多次求解本征模态分量(IMF)平均值,消除在非连续点白噪声对于原始信号的干扰[12]。
数据预处理步骤如下:
步骤1将故障数据划分为若干个样本数据,对每个样本数据x(t)样本数据较大添加正态白噪声Sw(ω),得到一个新的整体xs(t),即
xs(t)=x(t)+Sw(ω)。
(9)
其中正态白噪声Sw(ω)的表达式如下:
(10)
式中:Rw(l)=σ2δl,l=0,±1,±2,…。
(11)
(12)
步骤2对已添加白噪声的样本数据xs(t)进行EMD分解,得到若干IMF分量,其表达式如下所示:
式中:imfc(t)为EMD分解的第c个IMF;rn(t)为分解n个IMF后的参与分量。
步骤3重复上述步骤,每次加入新的白噪声序列。
步骤4将每次得到的IMF进行定积分并除以分段长度,为了防止分解后数值的正负号影响,故在之前先将IMF绝对值化处理。其流程图如图2所示。

2.2 PSO-ELM模型
ELM是由HUANG等[25]提出的一种针对单隐含层前馈神经网络(Single-hiddenLayerFeedforwardNeuralnetwork,SLFN)的算法。ELM具有训练参数少、学习速度快、泛化能力强大等特点,训练过程中随机生成了输入层和隐藏层之间的连接权重W和阈值B,然后连接权重与训练集的输入矩阵相乘叠加求和,由于W和B为随机生成,在一定程度上影响了ELM的准确度。而粒子群优化(Particle Swarm Optimization, PSO)算法可以有更多机会求解全局的最优解,同时还可以进行多目标优化,具有搜索速度快,效率高的优点。用PSO算法来优化ELM权重W与隐含神经元的阈值B以达到提升ELM准确度的目的。
过程1设输入层与隐含层间的连接权值W为:
(13)
设隐含层神经元的阈值B为:
(14)
将W与B分别作为PSO的速度与位置代入,得到最优解。
过程2定义适应度函数,从PSO的粒子中得到ELM的原始权值W和阈值B,使用n个任意不同的训练样本练习ELM神经元网络。
(15)
其中:i=1,2,3,…,n;xi=[xi1,xi2,…,xid]T∈Rd;ti=[ti1,ti2,…,tiK]T∈Rk;xi、ti分别表示训练样本输入的特征值和输出的真实值;d、k分别表示输入特征值与输出真实值的维数;L表示隐含层节点数;j=1,2,3,…,n;g(x)为其中的激励函数;βi=[βi1,βi2,…,βik]为隐含层第i个节点与输出层之间的连接权值。
Hβ=T。
(16)
将式(16)写为矩阵形式
(17)
(18)
(19)
其中:H为隐含输出矩阵;T为期望输出向量矩阵。
根据广义阵矩阵理论,求解式(16)的最小范数二乘解,从而求得β:
(20)
式中:H+为H的Moore-Penrose广义逆矩阵;E为单位矩阵;与HHT具有相同的维数;G为常量。
过程3测量粒子的适应度值,以均方根误差为适应度函数,求出个体的最佳值及其全局值。
过程4通过设定的目标误差判断是否达到迭代的终止条件,若达到目标误差,则将得到的最优的权值W和隐含层阈值B,如未达到,则返回上一层继续寻优,直到最大迭代次数为止。
其流程框图如图3所示。

2.3 模型性能测试
模型测试采用西安交通大学XJTU-SY轴承实验数据集[26],实验中采样频率设置为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。轴承的转速设置均为2 100 r/min,受到的径向力均为12 kN,每个样本包含32 768组数据,每组数据包含一个竖直方向加速度数据和一个水平方向加速度数据。由文献[27]可知,水平方向的振动信号能够包含更多的退化信息,故选取水平方向加速度标准差作为评判标准,采用了数据集中的Bearing1_1、Bearing1_4、Bearing1_5作为测试数据集,其对应的故障形式如表1所示,根据测试结果,无故障数据样本选取Bearing1_4前10个样本作为正常的数据集。

表1 轴承数据信息
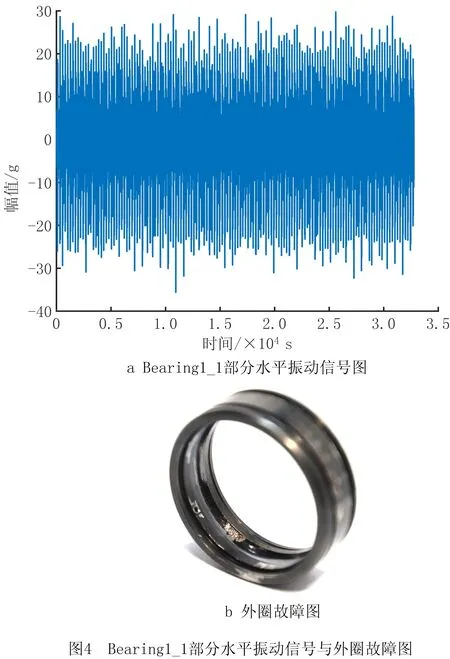
Bearing1_1数据集的部分水平方向的振动信号及故障形式如图4a和图4b所示,均值为-0.004 2,标准偏差为2.119 4。
Bearing1_4数据集的部分水平方向的振动信号及故障形式如图5a和图5b所示,均值为-0.004 9,标准偏差为0.466 3。

Bearing1_5数据集的部分水平方向的振动信号及故障形式如图6a和图6b所示,均值为-0.000 523,标准偏差为2.892 8。

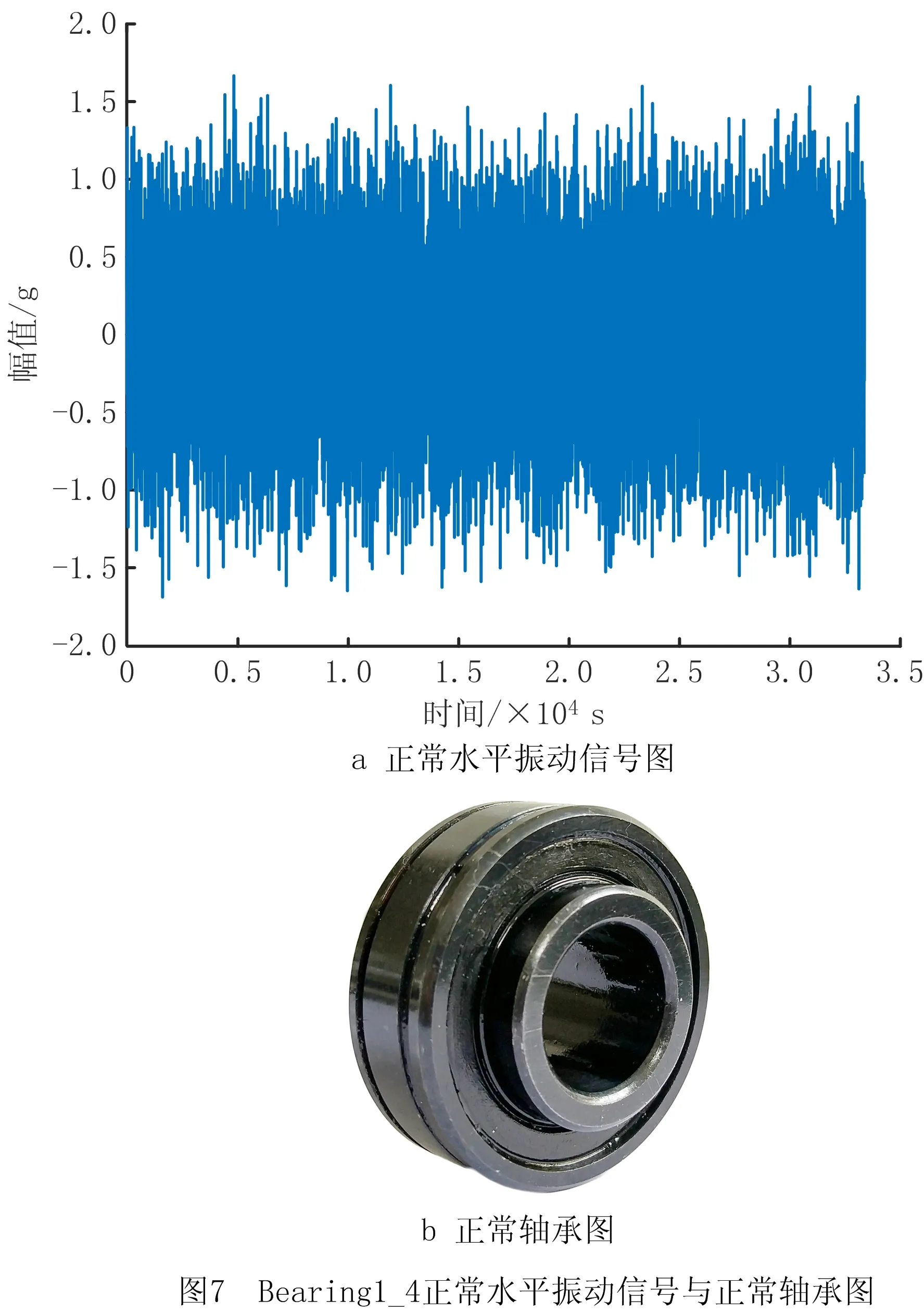
Bearing1_4数据集前10个样本的部分水平方向的振动信号及正常形式如图7a和图7b所示,均值为-0.004 4,标准偏差为0.428 2。
将数据样本均分为16组样本数据并对其进行EEMD分解。将分解后的IMF作为输入,分类号作为输出,其中分类1表示外圈故障、分类2表示保持架故障、分类3表示内圈、外圈故障,分类4表示正常。其输出结果如表2和图8所示。

表2 模型预测对比表
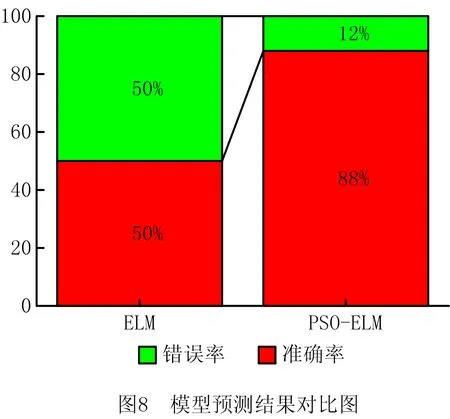
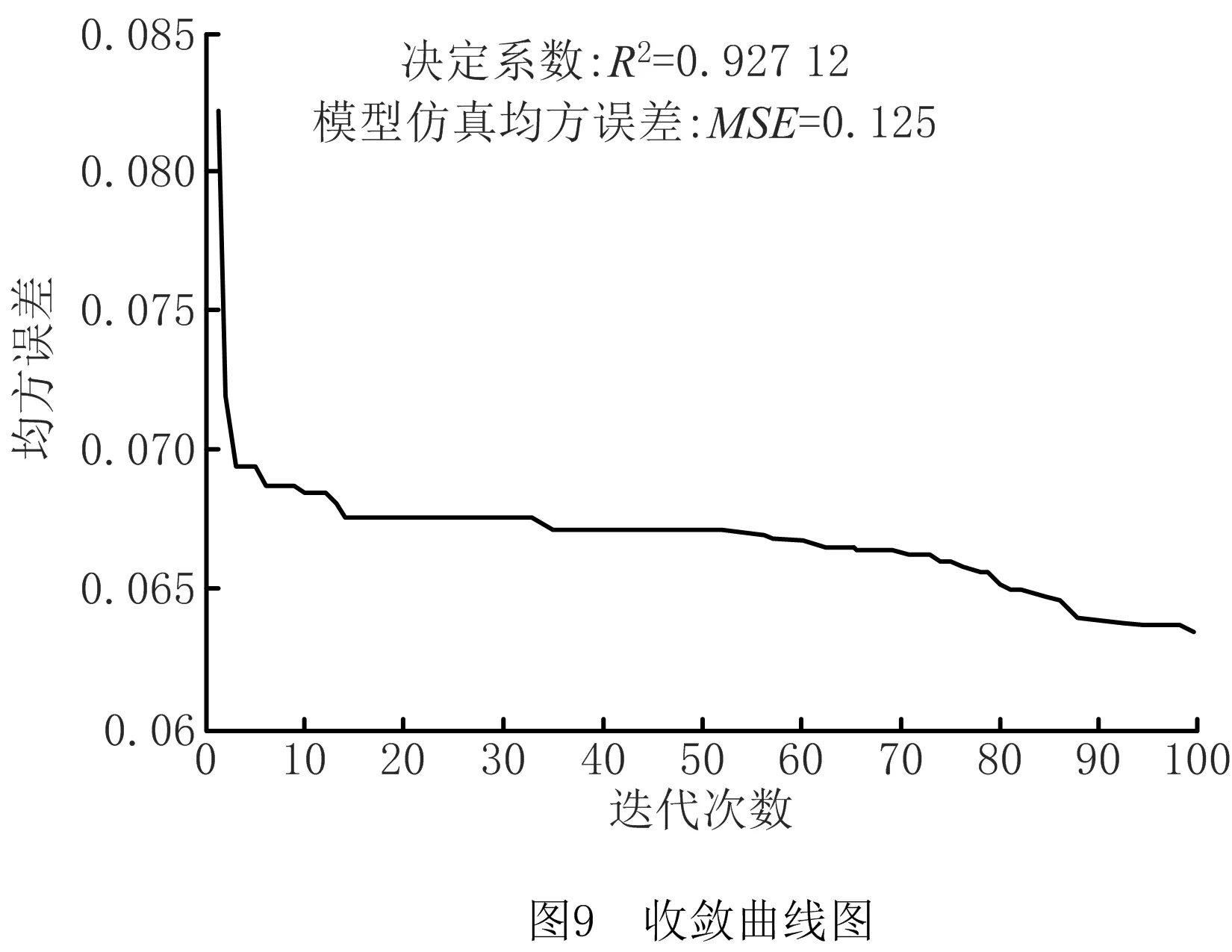
由表2和图8可以看出,PSO-ELM模型的预测准确度高于ELM模型预测准确度。PSO-ELM模型100次迭代误差变化如图9所示,由图9可以看出,PSO-ELM预测模型的性能较好,运行速度快,均方误差较小,稳定性较好。
3 试验及数据分析
3.1 试验平台
试验所用的RV减速器测试平台如图10所示,伺服电机的功率为5 kw,扭矩传感器的量程为15 N·m,力矩传感器的量程为200 N·m,磁粉制动器的规格为1.5 kw。主轴的转速设置为151 r/min,RV减速机的输入轴和输出轴均由扭矩传感器测得数据,RV减速机型号为RV-20E。每隔0.5 s采样一次,实验在常温下进行,共采集200 h的数据。RV减速器平台型号参数如表3所示。


表3 RV减速器平台型号参数
采集的试验数据如图11所示。
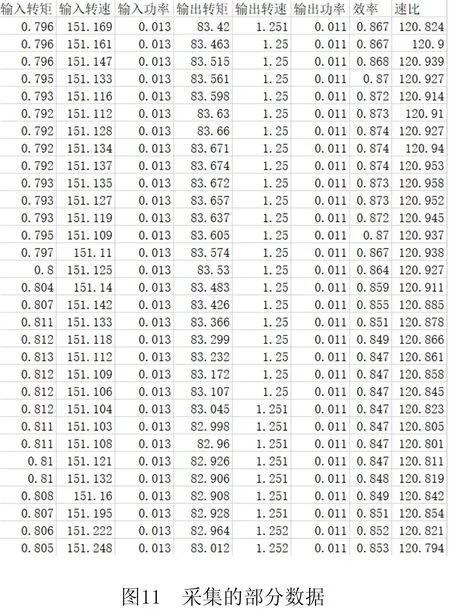
试验结束后,其扭矩、转速、功率出现反常数据,如图12所示,减速机出现故障。

为避免试验的偶然性,进行了多次试验的数据采集,选取故障前的数据和故障后的效率数据进行对比,如图13和图14所示。

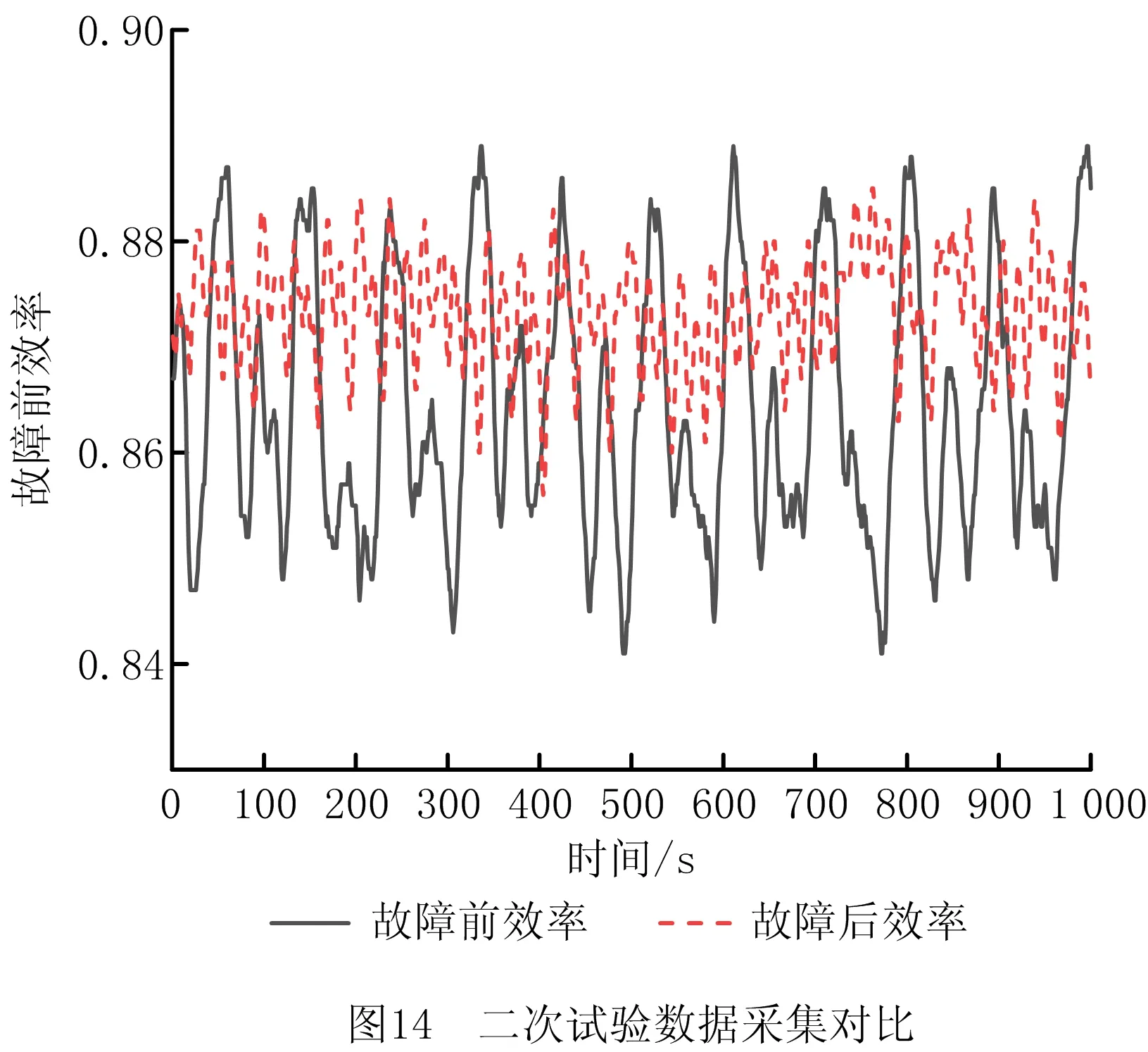
由图13和图14可知,故障前效率具备一定的周期性,故障后的效率周期性明显遭到破坏,符合式(8)的结论;拆解RV减速器后,发现曲柄轴磨损如图15所示;为了保证测试系统的传动刚度,轴向连接施加一定的预紧力,预紧力的施加及同轴度误差的存在,导致齿轮啮合存在一定偏载,故障后由于RV减速器曲柄磨损导致行星轮沿轴向发生微弱滑动,预紧力减小,曲柄轴杆力与轴向夹角减小,曲柄轴杆力径向分量减小,偏心距h减小,齿轮啮合偏载状态及润滑状态改善,啮合点处摩擦力减小,传动效率上升。

3.2 EEMD-PSO-ELM故障分类模型仿真
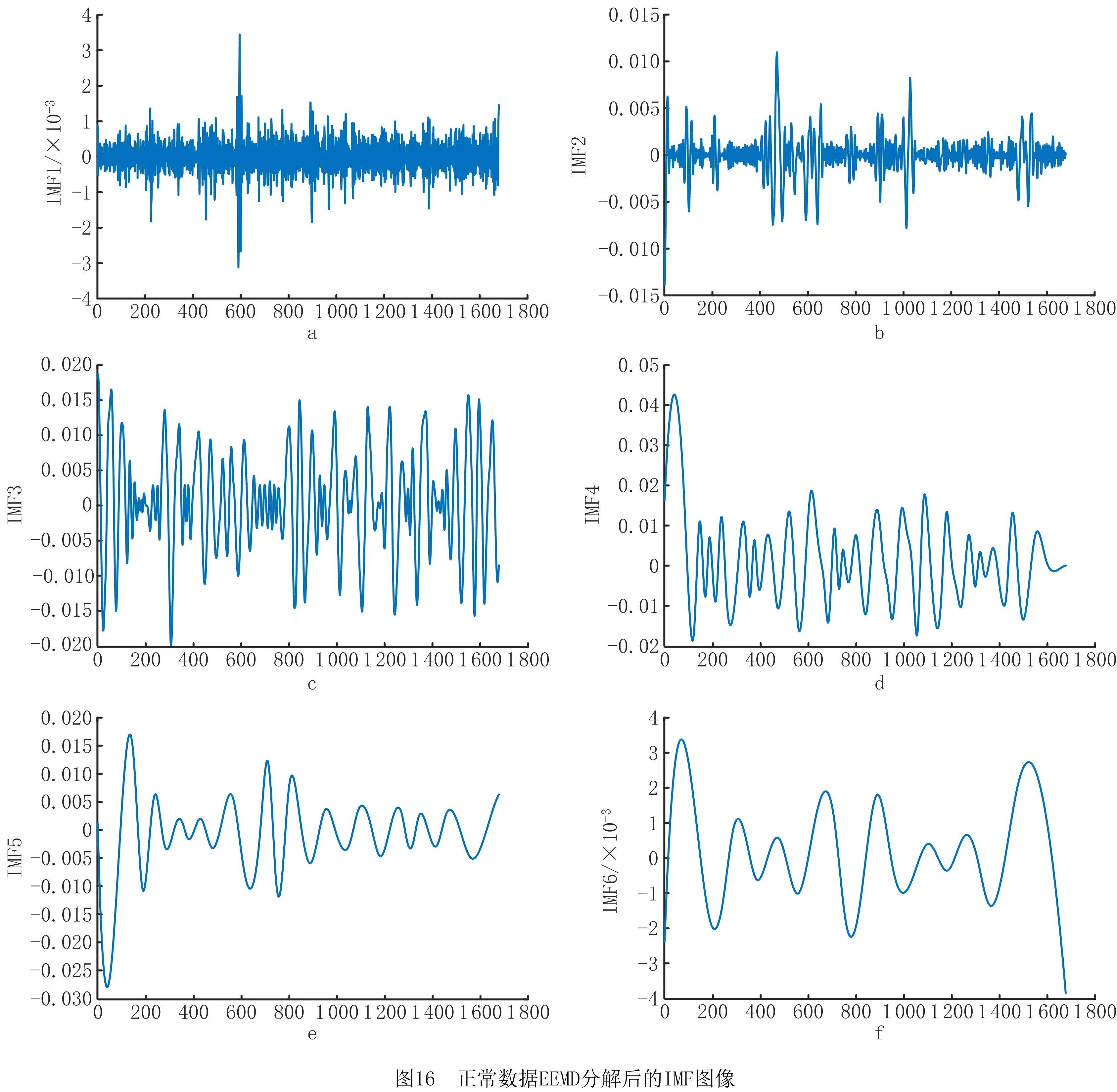
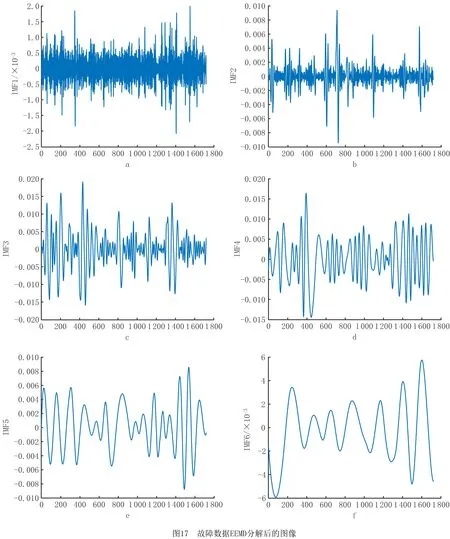
运用MATLAB R2018a编程,分别选取故障前效率和故障后效率1 680个监测数据作为样本数据,进行EEMD分解,得到的部分图形如图16和图17所示。
由图16和图17可以看出正常数据与故障数据在经过EEMD分解后差异明显。由于信号的能量主要集中在较低的IMF中[25],每组均取前6个IMF分量进行平均验算。
两组数据经过集合平均计算后分别得到21个特征值,此时将特征值输入PSO-ELM分类模型进行训练与分类,ELM隐含层神经元个数设定为5,激活函数为sigmoid;粒子的速度范围设置为-1~1,位置范围设置为[0.3-0.9],最大迭代次数设置为100,c1设置为2.8,c2设置为1.3。
在运行EEMD-PSO-ELM模型时,同时与ELM、EEMD-ELM、EEMD-PNN、EEMD-GRNN、EEMD-DE-ELM和EEMD-GA-ELM 6种模型进行对比,其结果如图18和图19所示:
由图18可以看出,ELM的识别准确率最低,为30%,在加入EEMD后,准确率有了明显提高,达到了60%,效果较为显著,但概率神经网络(Probabilistic Neural Networks, PNN)和广义神经网络(General Regression Neural Network, GRNN)表现较差,准确率分别为50%和40%,而差分优化算法(Differential Evolution, DE)优化的ELM在本次运行效果并不明显;遗传算法(Genetic Algorithm, GA)优化的ELM在本次运行效果较为明显,准确率达到了80%;EEMD-PSO-ELM识别模型在本次运行结果的准确率达到了90%,优化效果最为显著。
为排除试验结果的偶然性,共运行20次,其结果如图19所示。

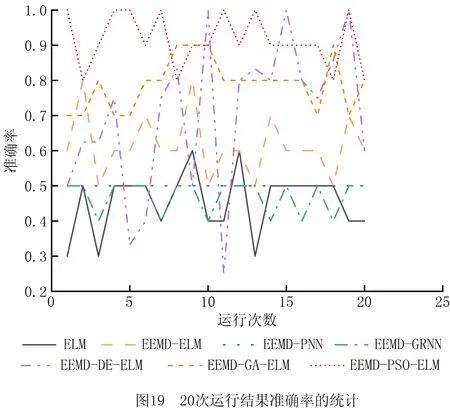

表4 运行20次后各模型准确率统计 %
由图19和表4可知,ELM模型的准确率最低,且不稳定,准确率经常在30%~50%之间浮动,整体的准确率只有45.5%;加入EEMD后的ELM准确率有了明显提高,整体的准确率达到了61.5%,但不稳定,在50%~80%之间浮动;而EEMD-PNN模型和EEMD-GRNN模型虽然稳定,但准率却没有EEMD-ELM模型高,整体准确率分别只有50%和47%,表明了ELM的准确度比一般的神经网络更高;而EEMD-DE-ELM模型虽然偶尔的准确率达到100%但其准确度最低能达到20%,极不稳定;EEMD-GA-ELM模型准确率较高,多数在80%左右,偶尔会达到90%。EEMD-PSO-ELM模型整体准确率最高,20次的平均准确率达到了91.5%,整体准确率在90%以上,甚至有几次达到100%,准确率较为稳定。
综上所述,EEMD-PSO-ELM工业机器人RV减速器故障诊断模型的准确度和稳定性均优于另外6种模型。
4 结束语
本文将RV减速机测试平台所测得的数据经过EEMD法分解出RV减速器在故障时的特征值,包含效率监测数据潜在特征。将ELM的连接权值W及隐含层神经元阈值B用PSO进行优化,从而提升ELM的预测精度和稳定性。将特征值作为输入导入到PSO-ELM故障识别模型。
以此构建的EEMD-PSO-ELM工业机器人RV减速器故障诊断分类模型与ELM、EEMD-ELM、EEMD-PNN、EEMD-GRNN、EEMD-DE-ELM、EEMD-GA-ELM模型相比,该模型更加快速、精确度更高且更稳定。
及时准确地判断出RV减速机运行状态有利于对RV减速机进行及时的维护,能有效地帮助工厂及企业降低损失,更可以在一定程度上帮助RV减速机测试厂家提升测量RV减速机测试数据的准确度,从而达到减少RV减速机使用厂家的经济损失,提升RV减速机使用厂家效益的目的。
未来,作者团队将继续在基于深度学习的工业机器人RV减速器故障诊断和在线健康评估方向开展持续性研究。

