基于交替混合迭代搜索方法的预制构件生产调度与工人配置集成优化

熊福力，杜 瑶，曹劲松，汪琳婷

(西安建筑科技大学 信息与控制工程学院，陕西 西安 710055)

0 引言

装配式建筑现已成为国家和行业大力发展的新型建筑模式，具有施工时间短、生产效率高、环境污染小等特点。预制构件作为装配式建筑中极为重要的一环，也受到了这种新兴建筑模式发展带来的机遇和挑战。然而，对于国内现阶段预制构件生产模式而言，全自动化生产方式现在还为时过早，所有预制件工厂都采用机器处理与工人作业共存的方式。因此对于这种生产模式，同一项工作的效益可能随所配置的工人不同而有很大的区别。这也导致相同工序的处理时间的可变性，最终将影响生产调度的可靠性。这种缺陷将造成生产管理效率低下、生产计划失效，潜在地导致运营混乱、工期延长和供应链成本增加。因此，工人配置与预制构件生产调度的集成优化对现阶段预制构件生产调度研究具有重要的理论意义和实用价值。

在预制构件生产调度问题上，近年来已取得一定的成果。CHAN等[1]以最小化完工时间和拖期/提前交货惩罚成本为目标建立了流水车间调度模型(Flow Shop Scheduling Model, FSSM)；KO等[2]在此基础上建立了预制构件生产六阶段生产模型；YANG等[3]以最小化空闲时间、拖期和提前惩罚、存储成本、完工时间等目标建立了多预制生产线的FSSM。随后WANG等[4]提出了改进的九阶段生产调度模型，并考虑了模具制造、预制件存储和运输等因素对生产过程的影响。熊福力等[5]以最大化总净利润为目标解决了预制构件生产中交货期配置、订单选择与生产调度的同时决策问题。秦璇等[6]则考虑了预制构件生产过程中受资源约束的多目标调度问题。上述研究缺乏实现生产成本和及时交货这两个相互冲突的目标之间权衡的方法。此外，实际生产中会有一定因素的干扰，每道工序的处理时间会随着工人资源配置的不同而不同，进而对生产调度造成直接影响，但以上研究中皆把每道工序的处理时间设置为固定值，即假定工人资源已经配置好，在实际生产过程中往往需要根据实际订单情况，对工人资源和生产调度进行集成优化。

在考虑劳动力资源的调度优化方面，YURA[7]首先加入了对人员因素的考虑，提出员工对于生产进度表的满意度是维持员工士气的重要原因，理想的生产计划应根据员工的工作日、休假、加班等偏好调度，提出在到期日约束下满足工人的偏好；THOMPSON等[8]考虑使用具有不同生产力的员工组来制定劳动力计划的问题；ELSHAFEI等[9]提出一种动态规划(Dynamic Programming, DP)算法，解决具有若干实际休假时间约束的人工调度问题，并给出了每个员工的工作顺序所决定的成本结构，同时提出一个适合于中等规模实例的DP算法来确定最优的工作分配，使总人工成本最小化，同时在规定的约束条件下满足工作需求；PAN等[10]提出一种具有两阶段启发式算法的混合整数规划模型，用于解决精密工程行业的人力调度问题，并提出一个两阶段的启发式算法，第一阶段通过考虑作业，机器和其生产计划来计算每个班次的技能要求，第二阶段通过考虑技能及来分配操作员到机器；ZHANG等[11]开发了一种改进的学习曲线来代替对数线性学习曲线，以监控工人绩效的提升，还考虑了工人先前的经验和机器在学习过程中的影响；AHMADIAN FARD FINI等[12]提出一种数学模型，用于确定机组人员具有不同经验水平的单技能和多技能工人的最佳组合，以通过考虑多技能、不同技能水平和学习对机组人员的重叠影响来最大限度地缩短建设项目的工期生产率;陈俊杰等[13]建立了考虑胜任力差异的人力资源受限多目标项目调度问题模型，提出两阶段优化算法。上述工人配置问题研究中，在装配式建筑背景下，尚未有集成预制构件生产调度与工人配置的研究，究其原因主要有以下两点：

(1)从研究背景层面看，装配式建筑背景下的预制构件生产属于新兴产业，发展时间较短，虽然目前已有一些针对预制构件生产调度问题的相关研究，随着实际生产管理问题的不断涌现，以及信息技术和优化技术的不断发展，还存在较大的研究发展空间。而本文所研究的问题就是其中之一。

(2)从问题本身层面看，预制构件生产工序之间的差异较大，具有可利用时间与不可利用时间混合、串并行混合、可中断和不可中断混合以及资源可利用时间和资源量受限等特点，通常来讲，即使是单一工人配置问题和单一的生产调度问题就已经是NP-hard问题，因此在这种复杂生产背景下，将二者集成优化无疑具有一定的挑战性，但同时对于提高预制构件生产企业净收益和改善客户满意度具有重要的意义。

基于以上分析，本文考虑了预制构件生产背景下的生产调度与工人配置集成优化问题，以期为预制构件制造企业及类似制造企业提供有价值的管理启示。首先以最小化工人成本和拖期惩罚总费用为目标建立了预制构件工人配置与生产调度集成优化数学模型，随后基于交替分解思想，提出一种交替式混合遗传—迭代贪婪搜索算法(Alternative Hybrid Genetic-Iterated Greedy Algorithm, AHGA_IG)，并通过大量计算实验验证了所提算法的有效性。

1 问题描述与数学模型

1.1 生产背景描述

预制构件生产一般包含6道工序：①铸模；②放置预埋件；③混凝土浇灌；④蒸汽养护；⑤脱模；⑥修复。每道工序仅有一台机器(即单生产线工作模式)。预制构件生产不同于传统流水车间问题，其生产工序分为可中断工序(如第1、2、5、6工序)和不可中断工序(如第3、4工序)。如图1中可中断工序情形1和情形2所示，可中断工序如果可以在工作时间内完成，则正常生产；否则，订单需继续处理至下班时间，剩余工作中断至次日工作时间完成。不可中断工序(如第3、4工序)指工序在处理完成前不能中断操作，否则会出现工件损坏等情况，不可中断工序如果在工人允许加班时间内可以完成则加班完成，否则该工序推迟于次日工作时间开始处理，如图1中不可中断工序且需要人工情形1和情形2所示。第4道工序蒸汽养护属于不可中断工序，但不需要工人操作，因此不受工作时间约束。其完工时间如图1中不可中断且不需要人工情形1～情形3所示。

不同的工人配置方案不但会造成订单处理时间的变化，影响订单的最大完工时间，而且配置不同等级或不同数量的工人需要支付的工人薪资成本也会随之变化。根据预制生产过程的实际工人需求，对各工序中所需工人数量进行约束，如表1所示。其中第4道工序为蒸汽养护，工厂采用全自动化方式处理，不需要工人干预且处理时间不随工人配置方案调整而变化。不同等级的工人具有不同的处理水平和操作熟练度，对同一订单的处理时间也不相同，同时也具有不同的薪资待遇。因此，对不同等级工人的工作效率和薪资水平作出如下假设：①将工人分为初级工人、中级工人、高级工人3种等级；②不同等级工人具有不同的工作效率ηl和薪资水平Wl；③工人等级越低，工作效率ηl和薪资水平Wl也越低。订单调整处理时间与原处理时间成正比，与分配工人的工作效率ηl和工人数量Nl,s成反比。为使模型更加精确，工人成本的计算采用绩效制，即以工人工作时间计算工人工资，若工作时间为0，则该工人没有工资。

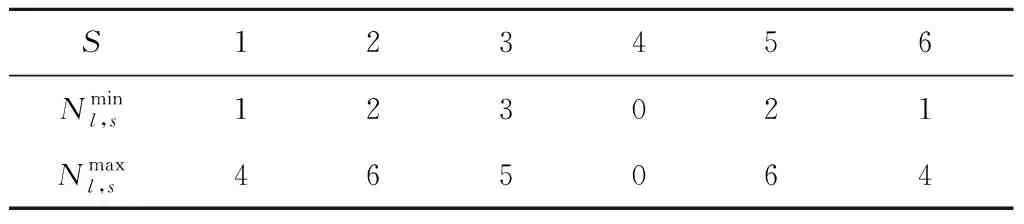
表1 各生产工序工人数量约束

1.2 问题描述

基于以上预制构件生产背景，预制构件生产调度与工人配置集成优化问题可描述如下：J个订单需要按照相同的处理顺序经过S道预制构件生产工序且订单在每道工序上只能处理一次，每道工序每次只能同时处理一个订单(第4道工序蒸汽养护除外，其采用并行处理方式)。各订单在各工序上所需的处理时间已知，但其会随工人配置方案的改变而变化，受工人配置方案影响的调整处理时间在订单处理前为已知。问题需要对各处理工序上的工人进行配置，计算工人配置后的调整处理时间，并以最小化工人成本和订单拖期惩罚为目标优化生产调度和工人配置。

为使问题更加明确，对生产过程作出如下假设：

(1)每道工序有且仅有一台机器；(2)所有工件、机器在调度零时刻均为可用状态；(3)所有工人在上班时间均为可配置状态；(4)所有工人均有能力处理所有工序；(5)每道工序配置的工人均为同一等级；(6)工序间缓冲区容量为无限；(7)不考虑工件恶化、人员请假和机器突发故障情况。

(8)各工人采用8小时工作制，允许加班时间不超过3小时，否则必须停止工作。即工作时间HW=8，可加班时间HO=3，非工作时间HN=16。

1.3 数学模型

基于以上问题描述，建立如下数学模型：

(1)标引和输入参数

J为订单数量;

N为工人数量;

S为工序数量;

L为工人等级数量;

j∶={1,2,…,J}为订单编号;

s∶={1,2,…,S}为工序编号;

l∶={1,2,…,L}为工人等级编号;

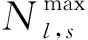
Pj,s为工序s上订单j的原处理时间;

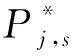
dj为订单j交货期;

βj为订单j单位时间拖期惩罚;

Wl为l级工人单位时间薪水;

ηl为l级工人工作效率;

HW为工作时间;

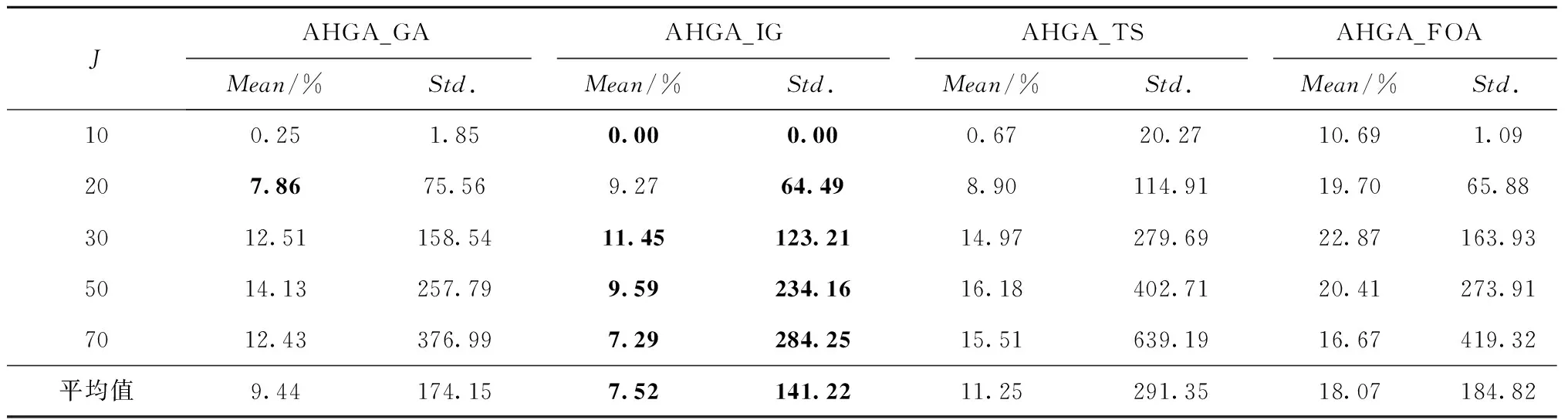
HO为可加班时间(HO

HN为非工作时间(HN=24-Hw)。

(2)决策变量

Xl,s为工序s中配置的l级工人的数量;

Yl,s为0-1决策变量，表示工序s中是否配置l级工人;

Cj,s为订单j在工序s上的完工时间;

Aj,s为订单j在工序s上的累计完成时间。

(3)目标函数

(1)

(4)约束条件

(2)

(3)

s∈{1,2,5,6},∀j；

(4)

s∈{1,2,3,5,6},∀j；

(5)

(6)

Cj,3=

(7)

Cj,4=

(8)

(9)

(10)

(11)

(12)

(13)

Xl,s,Cj,s≥0,∀l,s；

(14)

(15)

从以上模型可以看出，从变量角度看，模型中既包括连续变量(如Cj,s)，也包括离散变量(如Xl,s和Yl,s)。从约束角度看，模型中既包括线性约束(如式(2)和式(3))，同时还包括非线性约束(如式(4)～式(8))。综上所述，该模型难以利用现有商业优化软件进行直接求解。

本文所研究的问题具有如下特点：①从研究对象层面看，本文所研究的预制构件流水车间具有可利用时间与不可利用时间、串并行混合、可中断与不可中断混合、不同技术等级工人混合等生产特点，比传统的流水车间更为复杂。②从问题求解层面看，本文所研究的问题，是比传统单一流水车间调度问题或者单一的工人资源配置更为复杂的多决策离散集成优化问题，需要以拖期惩罚和工人成本费用最小化为目标，根据预制构件企业机器资源和劳动力资源能力以及客户实际需求，同时对工人配置和生产调度进行综合决策，对生产调度方案和工人配置方案作出综合决策。需要指出的是，传统的单一流水车间调度和工人资源配置问题在大多数情况下都是典型的NP-hard问题[14]，对于中大规模问题，精确算法通常难以在合理的时间内求得最优解，因此，对于本文的集成优化问题，将通过深入分析问题结构，集成构造启发式、最优交货期配置、邻域搜索以及破坏—构造机制，提出有效的混合智能优化方法，克服整数变量、多决策属性和大量非线性复杂约束带来的求解困难。

2 算法设计

生产调度与工人配置是预制构件生产中两个非常重要的管理问题。其中工人配置会对预制构件生产各阶段处理时间和生产成本造成较大影响，而各阶段处理时间又会对生产调度结果产生直接影响；同时生产调度方案也会对不同等级工人资源配置策略产生直接影响。而在已有对于工人配置问题研究的文献中，通常采用工人配置与生产调度的递阶优化，而没有考虑生产调度方案也会对工人配置造成影响[14]。因此生产调度与工人配置二者的集成优化尤为重要，但这也无疑增加了求解难度。为降低问题求解难度，本文借鉴分解协调的思想，将原问题分解为工人指派层子问题和生产调度层子问题，通过两个子问题的求解结果信息交互，交替求解改进每个子问题的解，进而优化原问题的总目标值。具体来说，基于交替分解思想，通过集成构造启发式、群体搜索、邻域搜索和破坏—构造机制，提出了一种混合遗传—迭代贪婪交替搜索算法(AHGA_IG)：其主要思想是首先利用启发式方法产生一初始工人配置和生产调度解；随后，固定生产调度方案，设计一种混合遗传配置算法用于优化工人配置方案；反过来固定工人配置方案，设计一种迭代贪婪调度算法用于优化生产调度，如此两阶段交替优化，直到满足终止条件。

与传统流水车间调度问题相比，预制构件调度因为生产工艺中存在串并行混合、可中断与不可中断工序和资源可利用时间受限等特点，所以更为复杂。传统流水车间调度问题已被证明具有强NP难特性[15]，因此本文所研究问题同样属于NP难问题。对于此类问题，精确算法理论上虽然可以求得最优解，但是其求解时间随问题规模增大呈指数倍增长，很难在较短时间内给出满足工业实际需求的合理解决方案。鉴于智能优化方法在解决大规模组合优化问题方面的优势[1-6]，基于交替迭代框架，通过集成构造启发式、群体搜索、邻域搜索，以及破坏—构造机制，提出一种混合遗传—迭代贪婪交替搜索算法(AHGA_IG)。其算法流程如图2所示。在AHGA_IG中，首先根据启发式规则构造初始解，即初始化工人配置方案和生产调度方案；随后固定初始生产调度方案使用遗传配置算法优化工人配置方案；当满足工人配置终止条件时输出优化后工人配置方案，并计算订单调整处理时间；再使用迭代贪婪调度算法优化生产调度方案；当满足生产调度终止条件时判断是否满足总体终止条件，若未满足则返回工人配置阶段按照优化后生产调度方案继续优化工人配置方案，如此交替迭代优化。满足算法终止条件则输出优化后工人指派方案、生产调度方案、目标函数值。以下将对混合遗传—迭代贪婪交替搜索算法的编码方式、初始解构造、遗传配置算法、迭代贪婪调度算法和接受准则部分进行详细介绍。

2.1 编码方式

工人配置问题需要同时为各工序分配不同等级和不同数量的工人，采用双层整数编码方式。编码长度为S×n，n=J/n1为订单组数，n1为每组订单的数量。预制构件生产过程中，预制构件处理时间较长，在大规模生产问题中，若皆采用同一人员配置不符合实际生产要求，因此将n1个订单分为一组，每组订单之间产生不同的工人配置方案。每组工人配置方案中，第一层为分配给各工序的工人数量；第二层为分配给各工序的工人等级。为便于理解，给出如下实例，如图3所示。编码表示第1组(G1)中，第1道工序分配到2级(中级)工人3名；第2道工序分配到1级(初级)工人6名；以此类推，第6道工序则分配到1级(初级)工人4名；其他分组也同样如此。其中第6道工序为蒸汽养护，属于自动化过程，不需要工人操作，因此不进行工人分配，工人等级和工人数量均设为0。

调度层采用整数编码方式。其中编码表示为订单的编号，编号在序列中的前后顺序表示订单的处理顺序，位置越靠前，则处理优先级越高。如图4所示，该编码方式表示的订单处理顺序为：1→3→2→6→8→5→7→9→4→10，则在生产中订单将按照该顺序依次经过所有处理工序，不得抢占。

2.2 初始解构造

初始解的构造对算法的求解速度和解的质量有较大的影响，适合于问题的初始解能够显著提高算法的搜索性能。因此对初始化工人配置方案和生产调度方案进行如下说明：

工人配置阶段决策变量为各工序所分配的工人数量和工人等级。因此工人配置问题初始解构造采用最小化工人成本和最小化订单处理时间两种启发式规则。根据这两种启发式规则将产生两种初始解:①所有分组中的所有工序工人等级分配初级工人，且工人数量设定为工序人数约束的最小值。该初始解分配最小工人数和最低等级工人，将具有最小的工人成本。②所有分组中的所有工序工人等级分配高级工人，且工人数量设定为工序人数约束的最大值。该初始解将分配最高等级工人和最大工人数，将具有最高的处理效率，即最小的订单处理时间。

生产调度阶段中订单拖期惩罚和订单交货期密切相关，订单交货期越长，产生拖期惩罚的可能性越低或产生的拖期惩罚越小。因此，生产调度问题初始解将按照订单交货期排序，交货期越短则订单越早处理。

2.3 遗传配置算法

遗传算法(Genetic Algorithm, GA)通过模拟生物界中“适者生存”原则，对种群内的染色体使用选择、交叉、变异等操作来更新当前解，目前在指派问题的研究中得到广泛应用[16-17]。工人配置问题中采用遗传配置算法，利用双层编码表示工人配置方案，因此采用交叉、变异、选择3种操作来更新当前解具有较大操作便利性。以订单数量=20，每组订单的数量n1=10，即订单组数n=2为例，具体操作流程如图5a所示，工人配置方案当前解为(3,6,1,0,3,4,4,3,3,0,2,4;2,1,2,0,2,1,3,1,1,0,2,3)。首先使用轮盘赌法对种群进行选择操作，得到(3,6,1,0,3,4,4,3,3,0,2,4;2,1,2,0,2,1,3,1,1,0,2,3)，(3,4,1,0,2,3,2,4,3,0,1,1;3,2,3,0,1,2,3,1,2,0,1,2)两组解。随后使用交叉操作。在交叉过程中，首先对染色体第一层工人数量进行两点交叉，随机产生两个交叉点，将两交叉点间的染色体交换，保证交叉过程中互换的为相同工序的工人数量，保证满足工序上的工人数量约束。再对第二层进行两点交叉，随机产生两个交叉点，将两条染色体交叉点间的部分进行交换。对两层分别进行交叉操作，将增大对解空间的探索和开发。交叉操作将形成两条新的染色体(3,4,1,0,3,4,4,4,3,0,1,4;2,2,3,0,2,1,3,1,1,0,1,2)和(3,6,1,0,2,3,2,3,3,0,2,1;3,1,2,0,1,2,3,1,2,0,2,3)。最后对染色体进行变异操作，将变异点处配置的工人数量和等级按照约束重新配置。变异后形成两组新的解分别为：(3,4,1,0,5,4,4,4,4,0,1,4;2,2,3,0,1,1,3,1,3,0,1,2)和(3,6,1,0,2,1,2,3,3,0,2,4;3,1,2,0,1,3,3,1,2,0,2,1)。

2.4 迭代贪婪调度算法

迭代贪婪(Iterative Greedy, IG)算法是一种简单的算法，具有易于实现、效率高、参数少等特点，并且适用于任何考虑构造方法的问题。IG算法主要通过迭代破坏阶段和后续重建阶段来构建解决方案，再配合局部搜索与类似于模拟退火的接受准则来更新当前解。并且IG算法在求解生产调度问题方面已有应用并取得了较好的效果[18-19]。因此在解决调度层问题时设计了一种混合迭代贪婪调度算法，使用破坏操作、重建操作以及局部搜索来更新当前解。订单数量J=10为例，具体操作流程如图5b所示。生产调度方案的当前解为(1,3,2,6,8,5,7,9,4,10)。破坏规则为将解决方案中的部分部件剔除，产生不完全的解决方案，被破坏的方案构件为(2,5,10)，破坏后的解决方案为(1,3,6,8,7,9,4)。重建操作使用NEH(Nawaz-Enscore-Ham)启发式方法，将剔除的部件按照最优的方式重新插入不完全的解决方案中，重新构成完整的解决方案(5,1,3,10,6,2,8,7,9,4)。最后对完整的解决方案进行局部搜索，将前插点后面的解决方案插入序列最前方，形成新的解(9,4,5,1,3,10,6,2,8,7)。

2.5 接受准则

3 实验设计与计算结果分析

3.1 实验设计

遗传算法近年来在流水车间生产调度问题中有较多应用，并取得了良好的效果[20-21]，同样，禁忌搜索算法依据禁忌表特性避免重复搜索解决方案，大大提高搜索到全局最优解的概率和搜索效率，并且具有较强的避免陷入局部最优的能力，在生产调度问题中也有广泛应用[22-23]。果蝇算法为近年来流水车间中较为新颖的算法[24-25]。因此，为充分验证AHGA_IG算法的性能，本文还设计了混合遗传—禁忌交替搜索算法(AHGA and Tabu Search, AHGA_TS)、混合遗传交替搜索算法(AHGA_GA)和混合遗传—果蝇交替搜索算法(AHGA and Fruitfly Optimization Algorithm, AHGA_FOA)用于与AHGA_IG算法进行对比。AHGA_TS算法在生产调度层中将破坏和重建操作改为禁忌操作；AHGA_GA算法在生产调度层使用经典遗传算法实现；在AHGA_FOA算法中，调度层主要参考王凌等[24]提出的离散果蝇算法进行设计，使用嗅觉和视觉搜索过程对生产调度层问题进行求解。

目标函数为最小化工人成本与拖期惩罚，但由于各工厂具有不同的薪资待遇，当工人成本和拖期惩罚处于不同比重时，可能会对问题的结果有所影响。为测试不同薪资水平对实验结果的影响，将分为3种不同薪资水平情况对各算法进行实验。实验中所有算法均采用JAVA语言编程实现，代码测试环境为Intel i7_9750H/2.6 GHz/16.0 GB/IntelliJ IDEA。

各订单交货期dj按照[MK(1-τ-R/2),MK(1-τ+R/2)]均匀随机产生，其中MK为利用构造启发式得到的最大完工时间，τ为松紧系数，R为产生宽度。实验数据如下：订单数量J∈{10,20,30,50,70}，拖期惩罚系数βj∈{10,20}，每组订单数量n1=10。按照订单数量分为小(J∈{10})、中(J∈{20,30})、大(J∈{20,70})三种问题规模进行试验。每种订单规模生成10组不同测试算例，每组算例运行30次，避免随机误差对于试验的影响。对同一规模算例，为公平起见，所有算法均采用相同时间运行。为评估算法性能，定义平均相对偏差率(ARPD)如下：

(16)

其中：Fmin(Alg)表示当前算例中Alg算法取得的最小值(最小化问题的最优值);ref为当前测试算例的参考值，即所有算法在当前测试算例中取得的最小值。

3.2 计算结果

3.2.1 情形一：低等薪资水平

当工人处于低等薪资水平时，为测试3种算法的求解能力和算法间的差异。将各等级工人工作效率ηl及单位时间薪资Wl设置如表2所示。实验通过5种订单规模，分50组测试算例进行，将每种订单规模的10组算例结果取平均值，得到表3中各算法ARPD均值和标准差均值统计结果。由表3可以看出，AHGA_IG算法ARPD值最小，其中在订单规模为10时，ARPD=0.00%，说明其在该订单规模时每次都能求解得到3种算法中的最小值，在3种算法中具有较好的求解质量。AHGA_IG算法标准差在各个规模下均优于其他两种算法，说明该算法具有更好的鲁棒性。AHGA_GA算法在求解质量上略差于AHGA_IG算法，但优于AHGA_TS算法和AHGA_FOA算法。AHGA_TS算法平均标准差达到216.76，远超于其他算法，因此其鲁棒性较差，AHGA_FOA算法标准差与AHGA_IG算法相近，但ARPD值远超AHGA_IG算法，具有较差的求解质量。由此可知，AHGA_IG算法在工人处于低等薪资水平时较其他算法具有较强的求解质量和鲁棒性。

表2 各级工人工作效率及单位时间薪资表

表3 情形一各算法ARPD均值、标准差(std.)均值统计结果

3.2.2 情形二：中等薪资水平

在中等薪资水平下，将各等级工人工作效率ηl及单位时间薪资Wl设置如表4所示。各算法ARPD均值和标准差均值统计结果如表5所示。由表5中数据可以得出，当工人处于中等薪资水平时，就ARPD而言，AHGA_IG算法在各规模上均优于其他3种算法，具有较高的求解质量。就标准差而言，AHGA_IG算法在大多数规模小于其他算法，当订单数量J=20时，AHGA_GA算法优于AHGA_IG算法，但差距较小。AHGA_TS算法依旧在所有算法中标准差最大，具有较差的稳定性，AHGA_FOA算法ARPD值远大于其他算法，具有较差的求解质量。综合分析，AHGA_IG算法在此情形下依旧是综合性能表现较好的算法。

表4 各级工人工作效率及单位时间薪资表

表5 情形二各算法ARPD均值、标准差(std.)均值统计结果

3.2.3 情形三：高等薪资水平

在工人处于高等薪资水平时，各等级工人工作效率ηl及单位时间薪资Wl设置和各算法ARPD均值和标准差均值统计结果如表6和表7所示。从表7中数据可得，3种算法标准差较大，这是由于工人处于高等薪资水平，工人成本增大，导致目标值变大，标准差与目标值比值平均值为4.06%，处于合理范围。AHGA_IG算法ARPD和标准差值均小于其他算法，AHGA_TS算法在此情形下标准差和ARPD值优于AHGA_GA算法和AHGA_FOA算法，AHGA_FOA在标准差和ARPD方面均表现较差。由此可得，AHGA_IG算法在此情况下仍是求解性能和鲁棒性更优的算法。

表6 各级工人工作效率及单位时间薪资表

表7 情形三各算法ARPD均值、标准差(std.)均值统计结果

3.3 结果分析

以订单规模30为例，3种算法在各薪资水平下的收敛情况如图6所示。AHGA_IG算法在各薪资水平下均收敛最快，并且具有较高的求解质量。AHGA_FOA算法也能较快达到收敛状态，但其解的质量较差，AHGA_GA算法能够在较快达到收敛状态的同时兼顾解的质量，AHGA_TS算法则在收敛效果上表现较差。AHGA_IG算法各情形下在求解质量、鲁棒性均优于其他算法，在收敛性上，AHGA_IG算法均能够较快地达到收敛。因此，认为AHGA_IG算法相较于AHGA_TS算法、AHGA_GA算法和AHGA_FOA算法具有更好的求解能力、鲁棒性和收敛性，在预制构件生产调度与工人配置集成优化问题上表现更优。

现阶段各预制构件生产工厂多采用基于经验的启发式方式进行工人配置和生产调度，为验证AHGA_IG算法与启发式方式间求解性能差异，各工人薪资水平下算法改进率如表8所示。由此可得，AHGA_IG在各工人薪资水平下各订单规模均相比启发式方法求解性能有较大的提升，其中各工人薪资水平分别对应贫困地区、一般地区和发达地区的工人薪资。由此可得，AHGA_IG算法适用于各地区预制构件生产工厂，对预制构件生产调度问题与工人配置问题集成优化，具有较好的优化性能。

表8 各工人薪资水平情形下算法改进率 %

4 结束语

本文研究了一类预制构件生产调度与工人配置集成优化问题，充分考虑了预制构件生产工艺、工人配置以及资源受限等实际生产特点，以最小化工人成本和拖期惩罚为目标，建立了预制构件生产调度与工人配置集成优化数学模型，并提出一种有效的混合遗传—迭代贪婪交替搜索算法。并与AHGA_GA算法和AHGA_TS算法在不同工人薪资水平情况下通过不同数据规模订单进行了算法性能测试。计算结果显示，与其他两种交替式混合智能优化算法相比，AHGA_IG在搜索性能、稳定性和收敛性上均具有较好的表现，并且相对于预制构件企业常用的基于经验的启发式方法具有较大改进，平均改进13%以上，有望在实际应用中取得显著的经济效益并改善顾客满意度。

在预制生产6道工序中，第1,2,5,6阶段主要由人工完成，因此处理时间有一定波动，增加考虑工人配置的不确定处理时间和订单接收与调度问题将是下一步研究重点，并以此为目标，进一步挖掘问题特征，设计更高效的求解算法。