金属橡胶粘弹性阻尼迟滞力学与数值模型

吴瑞先，阮仕鑫, 2，吴芳，薛新，陈小超

(1. 福州大学机械工程及自动化学院, 金属橡胶与振动噪声研究所，福建 福州 350108； 2. 安徽信息工程学院机械工程学院，安徽 芜湖 241000)

0 引言

金属橡胶是一种以金属螺旋卷为原材料，通过冲压工艺制备而成的弹性多孔材料，具有承载能力强、 耐高低温、 耐疲劳、 环境适应性好等优点[1]. 当金属橡胶受到外载荷激励时，相互接触的金属螺旋卷之间相互滑动，产生滑动摩擦力，以热能的形式耗散能量，从而表现出阻尼耗能特性. 因此，金属橡胶通常作为各种减振装置的阻尼耗能元件，应用于振动控制领域[2-6]. 然而，由于金属橡胶具有很强的非线性，建立有效的力学模型描述金属橡胶的力学特性，成为国内外学者研究的热点问题.

部分学者将金属橡胶的空间结构简化为某一基本单元的组合，分析基本单元的受力特点建立力学模型，采用这种方法建立的理论模型称之为细观力学模型[7-13]. 细观力学模型虽然可以从本质上描述金属橡胶的力学特性，但其实际上是一种简化模型，无法精确描述金属橡胶的空间结构，存在一定的局限性. Zhang等[14]将金属橡胶分解为非线性弹簧单元、 干摩擦阻尼单元和粘性阻尼单元，提出非线性弹簧-干摩擦阻尼-粘性阻尼单元模型. 由于金属橡胶的阻尼成分比较复杂，理论建模比较困难，所以邹广平等[15]将金属橡胶的阻尼成分等效为粘性阻尼，将金属橡胶分解为非线性弹簧单元和粘性阻尼单元，提出非线性弹簧-粘性阻尼单元模型. 此外，部分学者[16-17]基于曲线分解的思想，将动态恢复力-位移曲线分解为弹性恢复力-位移曲线和阻尼恢复力-位移曲线，使用最小二乘法、 遗传算法等参数识别方法进行力学建模.

针对金属橡胶的有限元仿真问题，开展了不同方向的研究. 崔亮等[18]和邹龙庆等[19]基于悬臂梁模型建立有限元模型，仿真金属橡胶的迟滞力学特性. 邹广平等[20]将金属橡胶看成正交各向异性材料，仿真金属橡胶在随机激励下的加速度响应. 黄凯等[21]推导圆环形金属橡胶空间结构的数学方程，建立了金属橡胶参数化数值模型.

本研究基于曲线分解的思想，将动态恢复力-位移曲线分解为非线性弹性力-位移曲线和椭圆曲线，利用阻尼耗能相等的原理进行参数识别，建立描述金属橡胶迟滞力学特性的非线性弹簧-粘性阻尼单元模型. 将金属橡胶分解为非线性弹簧单元和粘性阻尼单元，仿真金属橡胶的迟滞力学特性. 研究结果对金属橡胶在振动控制领域的力学建模和工程应用具有指导意义.

1 非线性弹簧-粘性阻尼单元模型

1.1 力学建模

动态恢复力-位移曲线可以分解为速度大于零的上半支曲线和速度小于零的下半支曲线，如图1所示.

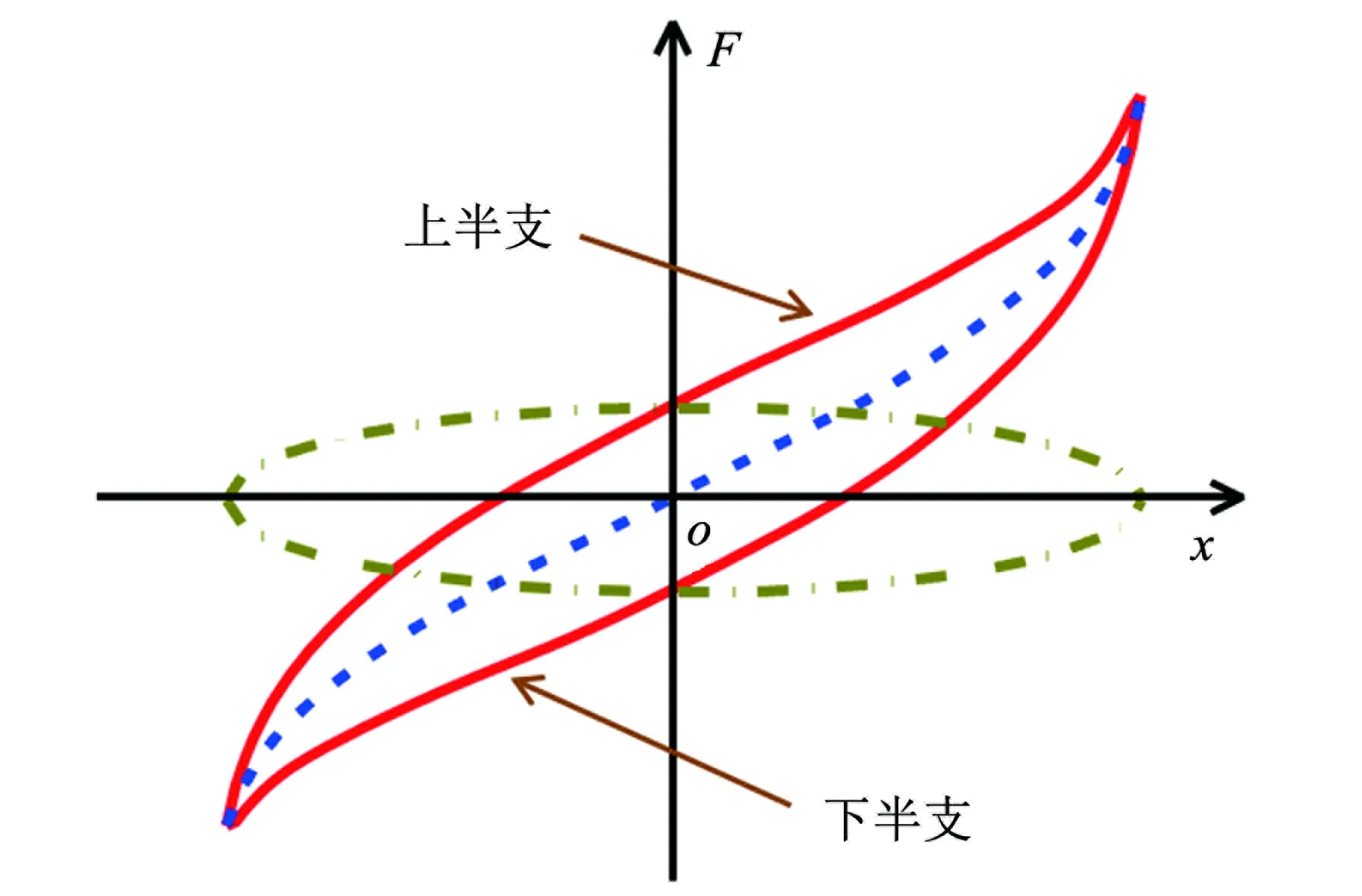
图1 动态恢复力-位移曲线

上半支曲线的方程为：

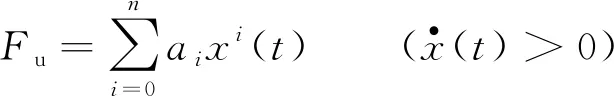
(1)

其中：Fu表示上半支曲线的动态恢复力；ai表示多项式系数；n表示多项式的项数；x(t)表示加载位移.

将式(1)按奇次项和偶次项分开的形式，可示为：

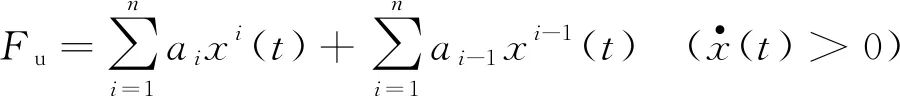
(2)

其中：i为奇数.

同理，下半支曲线的方程为：

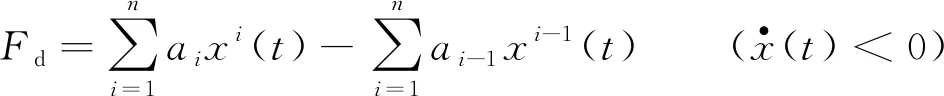
(3)

其中：Fd表示下半支曲线的动态恢复力.

结合式(2)和(3)，则动态恢复力-位移曲线的方程为：

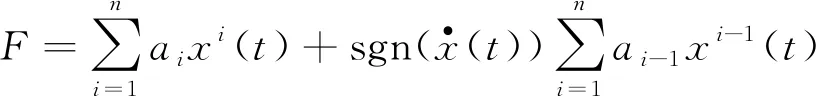
(4)

其中：F表示动态恢复力； sgn为符号函数.

从式(4)可以看出，表达式的第一项实际上是一条关于原点对称的奇函数曲线，第二项是一条关于横轴对称的曲线. 定义式(4)的第一项为非线性弹性力-位移曲线，第二项为粘性阻尼力-位移曲线.

由图1可知，粘性阻尼力-位移曲线近似为椭圆，所以式(4)可示为：

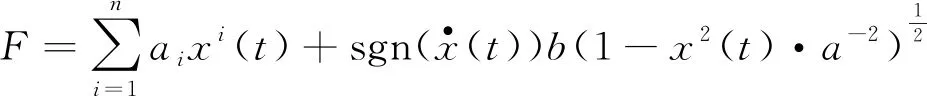
(5)

其中：a表示椭圆半长轴；b表示椭圆半短轴.

当外载荷为正弦激励x(t)=Asinωt时，椭圆半长轴a与正弦激励的振幅A相等，式(5)可示为：

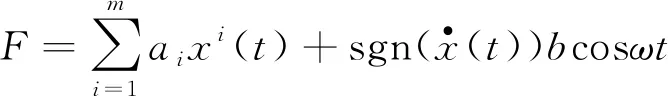
(6)

对正弦激励x(t)=Asinωt求导，可求得正弦激励的速度-时间关系：

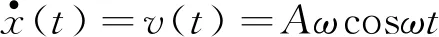
(7)

将式(7)代入式(6)，则动态恢复力-位移曲线的方程为：

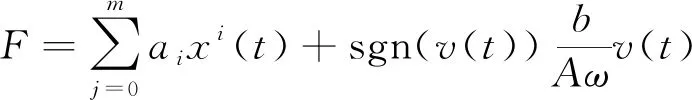
(8)

令等效粘性阻尼系数c=b/Aω，式(8)可示为：

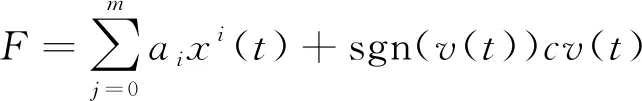
(9)

式(9)的第一项是非线性弹簧的力-位移关系，第二项是粘性阻尼材料的力-速度关系，则式(9)本质上是将金属橡胶分解为非线性弹簧单元和粘性阻尼单元. 该模型即为非线性弹簧-粘性阻尼单元模型.

若要得到动态恢复力-位移曲线的方程，需要对式(9)中的刚度系数ai和等效粘性阻尼系数c进行参数识别.

1.2 刚度系数的参数识别

根据曲线分解的原理，动态恢复力为非线性弹性力与粘性阻尼力之和，如：

Fu=Ft+Fcu;Fd=Ft+Fcd

(10)

其中:Fcu和Fcd分别表示椭圆曲线上半支和下半支的阻尼力.

由于椭圆曲线关于横轴对称，可得：

Fcu=-Fcd

(11)

将式(11)代入式(10)，然后将式(10)两式相加，可得：

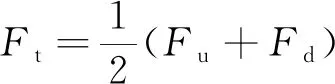
(12)

式(12)说明非线性弹性力-位移曲线为动态恢复力-位移曲线上半支和下半支的中线，利用式(9)的第一项对中线进行拟合，即可识别出刚度系数ai.

1.3 等效粘性阻尼系数的参数识别

非线性弹性力-位移曲线是一条单值曲线，说明非线性弹性力只影响金属橡胶的动态刚度特性，不影响金属橡胶的动态阻尼耗能，所以粘性阻尼力-位移曲线围成的椭圆面积代表了金属橡胶的动态阻尼耗能. 然而，动态恢复力-位移曲线的面积也代表了金属橡胶的动态阻尼耗能，根据动态阻尼耗能相等原理，该曲线面积必须相等. 基于上述分析，可得以下关系：

ΔWd=πab=πAb； ΔWd=∮Fdx

(13)

其中： ΔWd表示金属橡胶的动态阻尼耗能；A表示正弦激励的幅值.

将c=b/ωA代入式(13)，可求得等效粘性阻尼系数c：

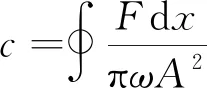
(14)

2 试样制备与试验方法

2.1 金属橡胶的制备

本研究所制备的圆环形金属橡胶内径为12 mm，外径为22 mm，长度为10 mm，分别制备密度为3.0和3.5 g·cm-3两种金属橡胶，成型压力分别为63和100 kN. 制备工艺流程图如图2所示.

图2 金属橡胶的制备工艺流程图

选用0.15 mm的304奥氏体不锈钢丝制备圆环形金属橡胶，制备主要分为如下3个步骤：

1) 将不锈钢丝绕制成类似弹簧形状的螺旋卷.

2) 将螺旋卷拉伸至合适的螺距，以交叉缠绕的方式制备缠绕毛坯.

3) 设计冲压模具，将缠绕好的毛坯装入冲压模具内进行冲压成型.

2.2 测试系统

测试系统采用长春机械科学研究院研制的SDS-200型高低温动静万能试验机，如图3所示. 测试系统的工作原理如图4所示.

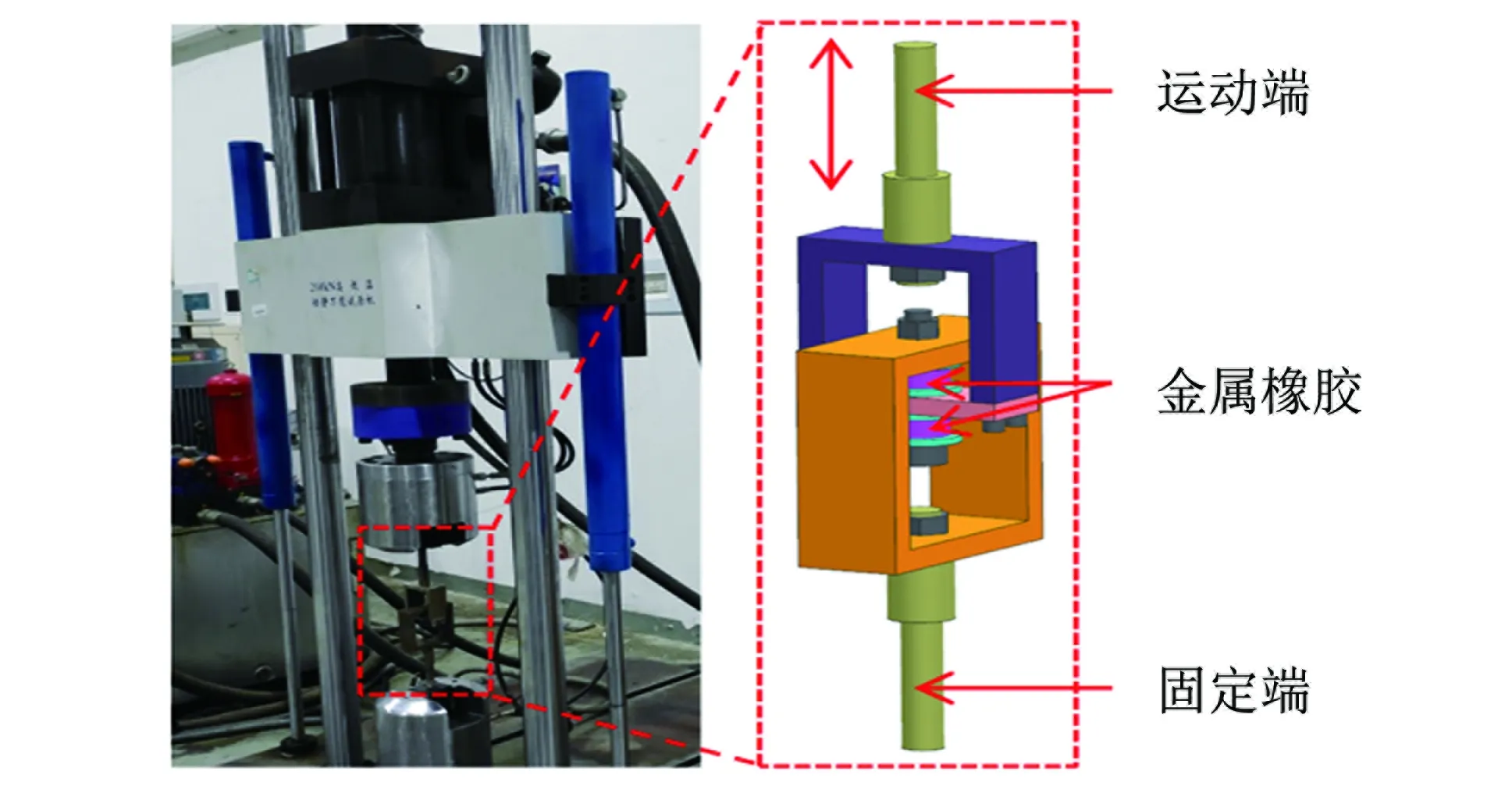
图3 动态测试系统

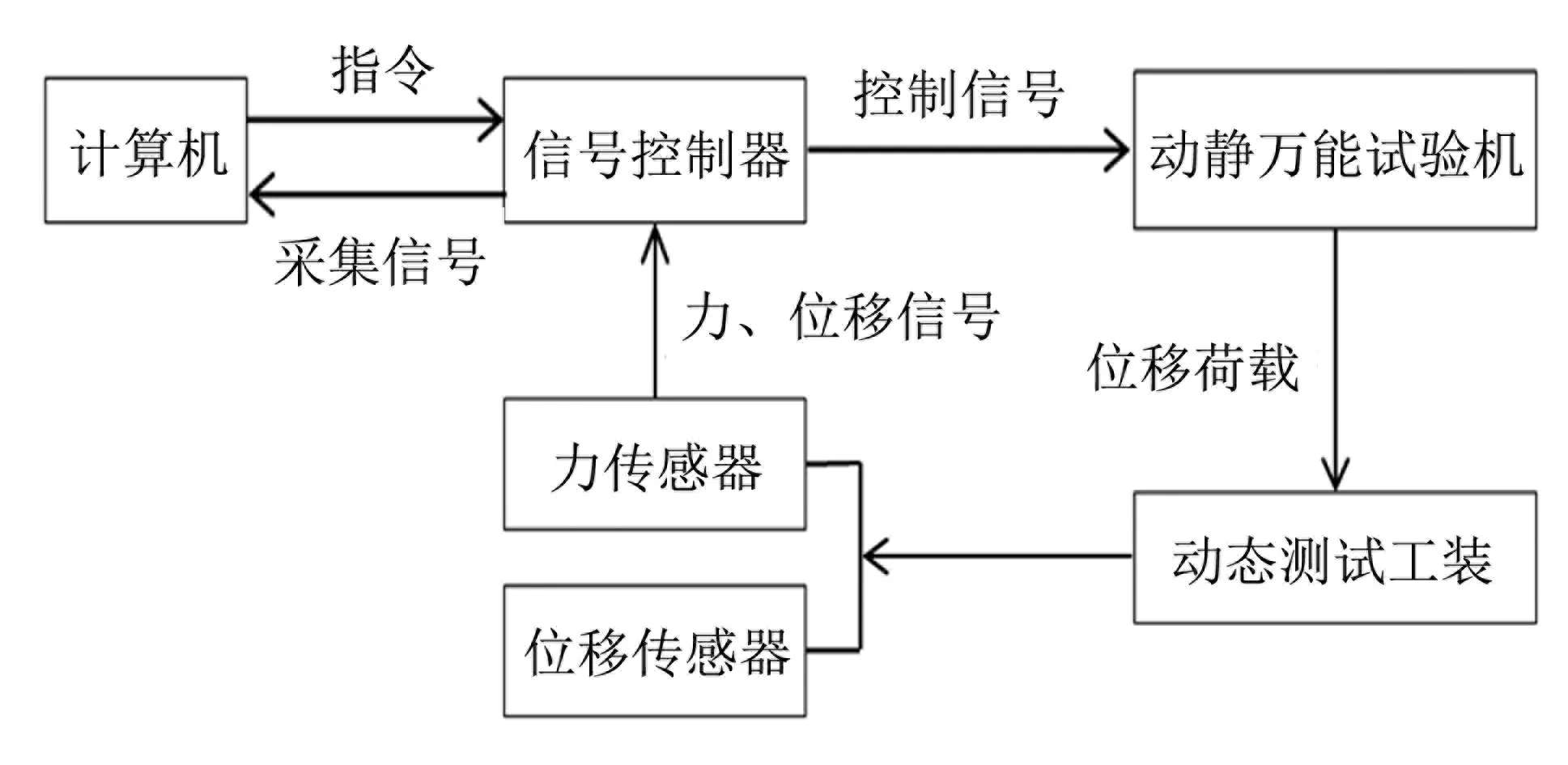
图4 动态测试系统原理图

本次试验采用正弦位移载荷加载，对密度为3.0 g·cm-3的金属橡胶采用固定频率为2 Hz, 加载位移振幅为1.0 mm； 对密度为3.5 g·cm-3的金属橡胶采用固有频率为1 Hz，加载位移振幅为0.6 mm.

3 实验验证

分别取动态恢复力-位移曲线上半支曲线和下半支曲线的平均值，得到非线性弹性力-位移曲线. 采用只含奇次项的5次多项式拟合非线性弹性力-位移曲线，识别出刚度系数ai，再根据式(14)识别出等效粘性阻尼系数c. 参数识别结果如表1所示.

表1 参数识别结果

动态恢复力-位移曲线如图5所示. 从图5可以看出，理论曲线和实验曲线的变化趋势较为一致，偏差也较小，所以非线性弹簧-粘性阻尼单元模型可以较好地描述金属橡胶的迟滞力学特性.

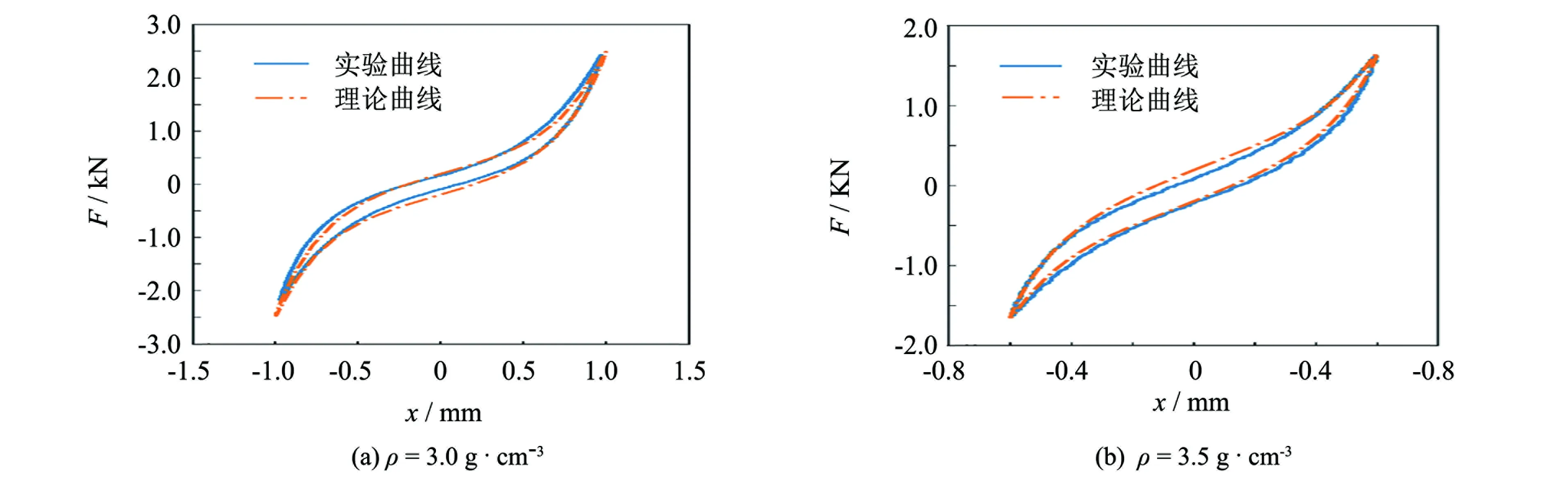
图5 动态恢复力-位移理论曲线

4 迟滞特性的有限元仿真

为研究金属橡胶的动态恢复力-位移曲线的仿真曲线，需要建立其有限元模型，设置单元类型、 材料属性，定义边界条件. 金属橡胶可以分解为非线性弹簧单元和粘性阻尼单元，非线性弹性属性可以模拟非线性弹簧单元的力学特性，粘性阻尼属性可以模拟粘性阻尼单元的力学特性. 通过理论模型定义单元的非线性弹性属性和粘性阻尼属性，再对模型进行仿真，即可得到动态恢复力-位移的仿真曲线.

4.1 有限元建模

从图3可以看出，运动端在关于零点位移对称的位置，金属橡胶对运动端的压力大小相等，方向相反. 因此，可以将金属橡胶等效为一个可以承受拉压载荷的连接器单元. 当运动端向上运动时，连接器单元对其产生向下的拉力； 当运动端向下运动时，连接器单元对其产生向上的压力.

基于上述分析，可以建立有限元模型，如图6所示.

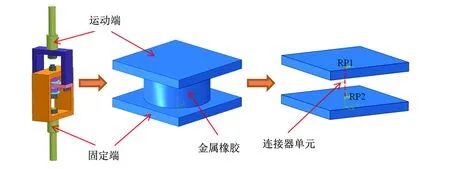
图6 金属橡胶等效模型

4.2 模型参数设置

Abaqus中的连接器单元可同时定义非线性弹性属性和粘性阻尼属性，所以可将金属橡胶等效为连接器单元，连接器单元的非线性弹性属性由式(9)的第一项决定，粘性阻尼属性由式(9)的第二项决定，根据表3的参数识别结果定义连接器单元的非线性弹性属性和粘性阻尼属性.

4.3 仿真结果及结论

按上述步骤设置模型并提交分析，仿真结果如图7所示. 通过对比图5和图7可以发现，动态恢复力位移曲线的仿真曲线与理论曲线变化规律基本一致，这是由于仿真值并不是通过拟合实验值的方式得到的，而是直接通过理论模型定义连接器单元的非线性弹性属性和粘性阻尼属性得到的，所以仿真值和理论值之间基本不存在拟合误差. 从图7可以看出，仿真曲线和实验曲线的变化趋势较为一致. 所以将金属橡胶等效为连接器单元，通过非线性弹簧-粘性阻尼单元模型定义连接器单元的非线性弹性属性和粘性阻尼属性，仿真金属橡胶的迟滞力学特性，具有较好的仿真精度.

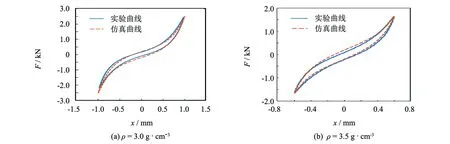
图7 动态恢复力-位移仿真曲线

5 结语

将金属橡胶分解为非线性弹簧单元和粘性阻尼单元的力学模型，提出描述金属橡胶动态力学性能的非线性弹簧-粘性阻尼单元模型和有限元仿真方法，得出如下3个主要结论：

1) 基于曲线分解思想的参数识别方法是有效的. 理论曲线和实验曲线的对比分析结果表明，该方法建立的金属橡胶粘弹性阻尼迟滞力学模型具有较高的精度.

2) 将金属橡胶的阻尼成分等效为粘性阻尼，可以将与位移成非线性关系的阻尼力简化为与速度呈线性关系的粘性阻尼，为含有金属橡胶的非线性系统的理论建模提供新的研究方法.

3) 将金属橡胶等效为连接器单元，通过非线性弹簧-粘性阻尼单元模型定义连接器单元的非线性弹性属性和粘性阻尼属性，是仿真金属橡胶迟滞力学特性的有效方法，具有较高的仿真精度.