基于二元维纳过程的水工闸门剩余寿命预测

杨 涛，张 钰 奇，李 凯 旋，韩 明 海，赵 华 东

(1.郑州大学 机械与动力工程学院，河南 郑州 450001； 2.河南省陆浑水库管理局，河南 洛阳 471000)

0 引 言

水工闸门随着运行年限的增加，会出现腐蚀、磨损等情况，从而严重影响闸门的运行安全[1-2]。一旦闸门出现破坏，会带来巨大的经济损失，甚至会造成人员伤亡[3]。目前，随着数字化、信息化技术的发展，对闸门进行健康状态评估越来越重要。剩余寿命预测作为健康监测的核心部分，对于指导闸门进行预测性维护以保证闸门安全运行具有重要意义。

近年来，闸门寿命预测方法越来越受到学者们的重视。赵林章等[4]利用分形维数法对闸门进行了寿命预测；Abdul等[5]计算了闸门侧轮和轨道的疲劳寿命；徐卫敏等[6]利用Gamma随机过程对钢板锈蚀量进行随机模拟，并采用Monte-Carlo法对闸门上某构件进行了时变可靠度计算；李伟康等[7]考虑到闸门锈蚀对材料性能会产生影响，基于D-H曲线推导出了闸门构件寿命预测的公式。但以上研究还存在着一些不足之处，主要体现在寿命预测的精度不高，用某个构件代替整个闸门，缺乏合理性。

基于随机过程的寿命预测方法可以很好地描述装备的不确定性，现已逐渐被应用于长寿命、高可靠度的装备寿命预测[8-9]。Huang等[10]基于逆高斯过程对刀具寿命进行预测，达到了较高的精度；Lin等[11]基于Gamma过程对锂电池剩余寿命进行了预测；Wang等[12]利用维纳过程建立了状态空间模型，并对轴承进行了寿命预测；Wu等[13]基于维纳过程对复杂机电系统进行了寿命预测。但是可以发现，以往研究未充分考虑闸门在运行过程中的复杂工况，且单个指标难以准确反映出其健康状态。Copula函数可以合理刻画出不同性能指标间的相关特性。Zhou等[14]运用Copula函数表征了腐蚀管道不同缺陷间的相关关系；Song等[15]利用Copula函数分析了轴承多种失效模式的相关性，并进行了寿命预测。因此本文采用多个指标进行寿命预测。

基于上述分析，本文选取闸门在腐蚀情况下变形和应力两个性能指标来表征其健康状态。首先，基于维纳过程对闸门变形和应力进行退化性建模；其次利用Copula函数分析其相关特性，得到闸门剩余寿命概率密度函数；通过分步极大似然估计法对维纳过程和Copula函数中的参数进行估计；最后对比分析了基于二元维纳过程和只考虑应力影响下的一元维纳过程进行寿命预测的精度，同时利用剩余寿命预测结果指导闸门确定了合理的维修时间。

1 基于二元维纳过程的退化建模

1.1 维纳过程

当采用维纳过程进行闸门退化建模时，第k个性能指标的退化过程可表示为

X(k)(t)=X(k)(0)+λ(k)t+σ(k)B(t)

(1)

式中：X(k)(t)为t时刻第k个指标退化值；X(k)(0)为退化初始值；λ(k)为漂移系数；σ(k)为扩散系数；B(t)为标准维纳过程。

1.2 基于Copula函数的相关性分析

由于闸门的变形和应力两个指标之间不是相互独立，也不是简单的线性关系，所以需要选择出合理的方法刻画不同指标间的关系。Copula函数能有效地将联合分布函数与边缘分布函数联合起来，常用于分析不同指标之间的相关特性。因此，本文利用Copula函数来分析闸门上多元性能指标之间的相关性，如式(2)所示：

F(x1，x2，…，xn)=C(F1(x1)，F2(x2)，…，Fn(xn))

=C(u1，u2，…，un；θ)

(2)

式中：F(x1，x2，…，xn)为各个变量联合分布函数；F1(x1)，F2(x2)，…，Fn(xn)为各个变量的边缘分布函数；C为Copula函数；θ为Copula中的参数。

Copula函数常见的4种类型如表1所列，其中u1，u2表示边缘分布函数。

由Sklar定理得，闸门变形和应力的相关特性可表示为[16]

F(x1，x2)=C[F1(x1)，F2(x2)；θ]

(3)

由于不同的Copula函数对于描述变形和应力两个退化指标的相关特性具有较大影响，所以应结合闸门实际退化情况选择合适的Copula函数。AIC信息准则鼓励数据拟合的优良性，被广泛运用于评价模型拟合数据效果的优劣。AIC值越小，则说明拟合的效果越好。本文采用AIC准则选择Copula函数：

AIC=-2lnA+2m

(4)

式中：A为模型对应的似然函数；m为模型中参数的个数。

2 剩余寿命预测模型

2.1 剩余寿命分布

当闸门两个性能指标均服从维纳过程时，其剩余寿命服从逆高斯分布[17]，剩余寿命的概率密度函数为

(5)

式中：ωk为第k个性能指标的失效阈值；xjk为第k个性能指标在tj时刻的性能退化值。

当获得闸门上变形和应力各自的剩余寿命概率密度函数后，由Copula函数可以得到应力和变形剩余寿命分布函数的联合概率密度函数：

(6)

式中：F1(t)、F2(t)为变形和应力剩余寿命边缘分布函数；c(F1(t)，F2(t)；θ)为C(F1(t)，F2(t)；θ)的概率密度函数。

定义变形和应力中任一性能指标超过失效阈值ωk，便认为装备失效。则闸门的剩余寿命T=min(T1，T2)。

因此，闸门剩余寿命的分布函数为

FRUL=P{min(T1，T2)≤t}

=F1(t)+F2(t)-C(F1(t)，F2(t))

(7)

闸门剩余寿命的概率密度函数为

(8)

2.2 参数估计

由于要估计的参数较多，分步极大似然估计法具有计算简单、流程清晰等优点，所以采用分步极大似然估计法更新模型中的参数。

(1) 由维纳过程的性质可知，增量服从正态分布：

(9)

式中：ΔXk为第k个性能指标退化量增量。

所以参数(λk，σk)的极大似然函数为

(10)

对λk，σk求偏导，可得λk，σk的极大似然估计值：

(11)

(12)

(13)

3 工程实例分析

陆浑水库溢洪道露顶式弧形钢闸门构件采用Q235钢，闸门面板中心弧面半径为12 m，面板、纵梁厚度为12 mm，支臂厚度为16 mm，主横梁厚度为18 mm，作用水头为9.84 m。闸门变形和应力作为闸门上重要的性能指标，在运行过程中会发生退化，可反映出闸门的健康状态状况。变形会影响闸门安全运行[18]，本文定义变形阈值为10 mm。根据SL 74-2019《水利水电工程钢闸门设计规范》，容许应力与闸门运行情况和钢材的厚度有关[19]。该弧形闸门最大应力处构件厚度均不大于16 mm，属于钢材尺寸分组中的第一组，同时取修正系数K=0.9，所以定义闸门上最大应力阈值为144 MPa。

本文采用文献[20]中所论述的Guedes Soares锈蚀深度非线性变化公式，如式(14)所示，并根据文献[21]中的统计数据确定参数，计算时段取13 a，同时利用有限元仿真得到闸门不同年份上的变形和应力变化。

(14)

式中：d∞为腐蚀量的长期厚度，全面腐蚀取d∞=1.6 mm，局部腐蚀取d∞=2.5 mm；d(t)为t时刻的腐蚀量厚度；τc为涂层寿命，取τc=5 a；τt为过渡时间，取τt=4.5 a。

由于ANSYS中的APDL模块有着简单的格式，可以方便对有限元模型进行计算，所以利用APDL对弧形钢闸门进行参数化建模和求解。由于闸门属于空间薄壁结构，因此采用shell 181单元进行建模。闸门上锈蚀主要分为全面锈蚀和局部锈蚀：对于全面锈蚀，采用平均蚀余厚度法进行模拟；对于局部锈蚀，通过改变锈蚀坑所在位置节点的厚度来实现对锈蚀坑的模拟[22]。根据闸门实际运行情况，局部锈蚀一般情况下出现在闸门的面板右下角漏水的部位、右下角边梁处以及下主梁经常性积水区域，所以通过改变上述区域的节点厚度实现对局部锈蚀坑的模拟。闸门的局部锈蚀区域如图1所示。

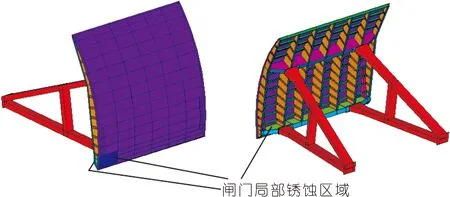
图1 闸门局部锈蚀区域Fig.1 Local corrosion area of gate

利用APDL对闸门进行有限元分析，可以得到闸门的变形和等效应力。闸门初始状态的变形和等效应力云图如图2～3所示。

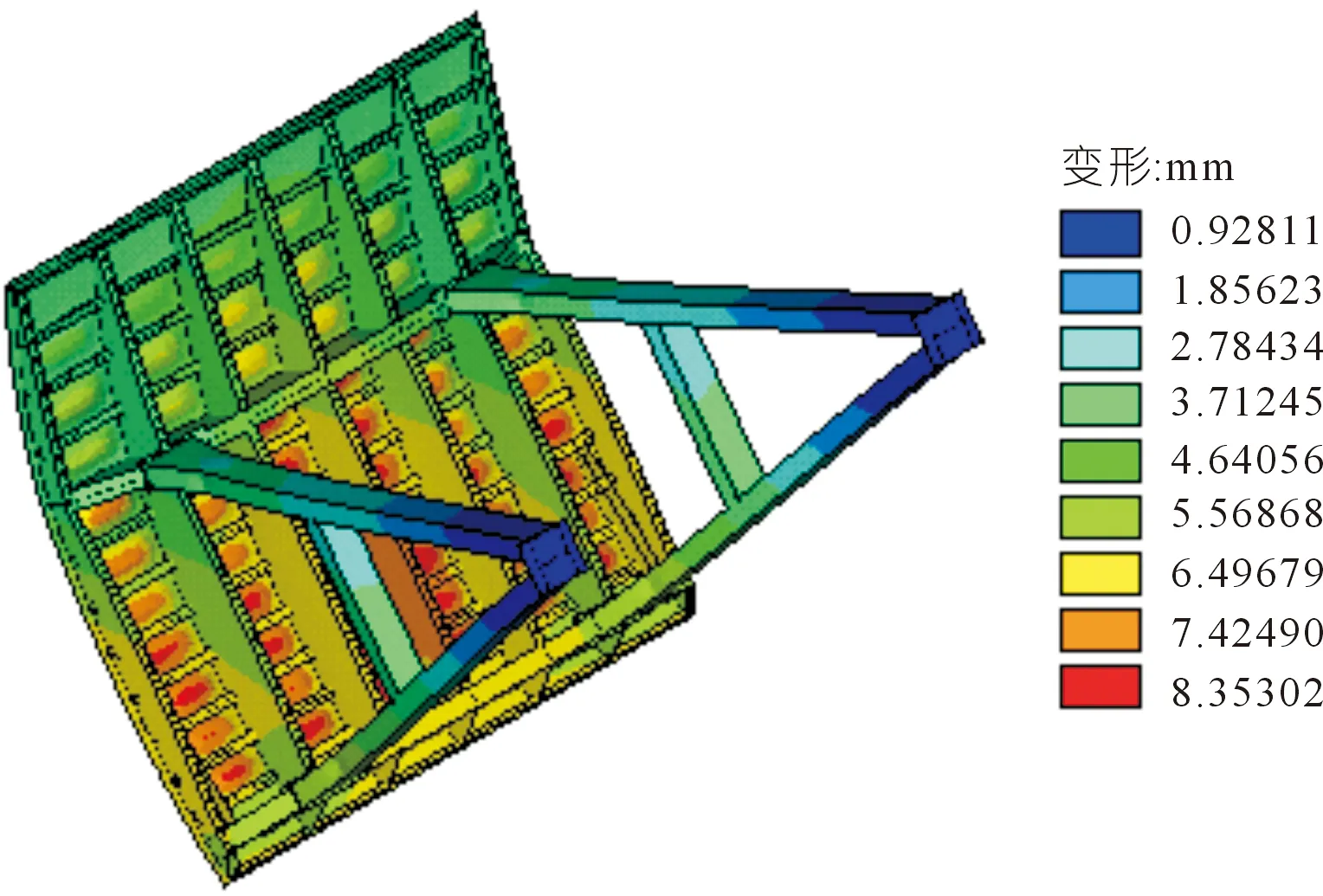
图2 闸门变形云图Fig.2 Gate deformation nephogram

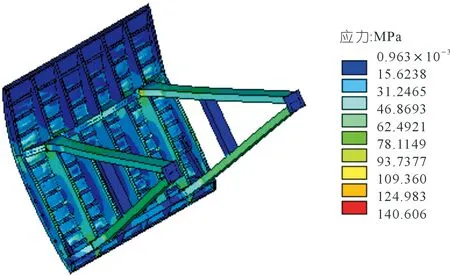
图3 闸门应力云图Fig.3 Gate stress nephogram

根据腐蚀非线性规律改变闸门对应部分的厚度，同时利用APDL仿真可以得出闸门在退化过程中不同运行年限的变形和等效应力，将不同运行年限的闸门变形和应力值连接成线，可以得到闸门上变形和应力退化曲线，如图4所示。

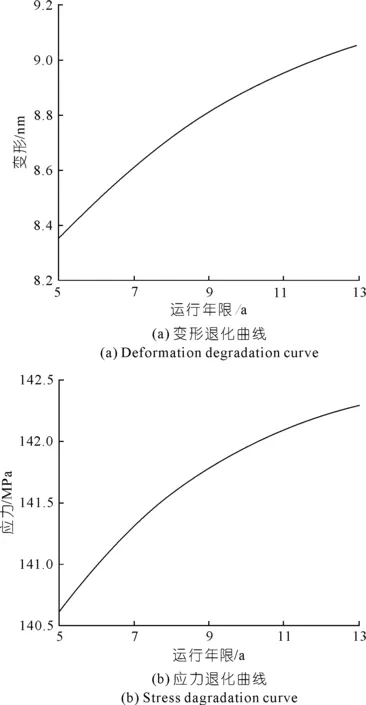
图4 闸门性能指标退化曲线Fig.4 Degradation curve of gate performance indices

为了验证使用维纳过程模型对闸门因腐蚀而产生的退化过程建模是否合理，需要对变形和应力退化数据进行检验。由于K-S检验法能够利用样本数据推断样本的总体是否服从某一理论分布，因此利用K-S检验法对闸门退化数据进行检验，检验结果如表2所列。其中：h=0表示在置信水平为α=0.05时接受退化量增量为正态分布的原假设，h=1时表示拒绝原假设；当p>α时，表示不拒绝退化增量为正态分布的原假设。通过分析可以看出闸门上的变形和应力退化量均满足正态分布假设，故可以采用维纳过程模型来描述闸门退化过程。

表2 K-S检验结果

通过式(5) 得到变形和应力的剩余寿命边缘概率密度函数后，利用AIC准则选择合适的Copula函数，不同Copula函数得到的AIC值如表3所列。由表3可以看出：Gumbel函数的AIC值最小，所以选择Gumbel函数来分析变形和应力的相关特性。由Gumbel函数得到变形和应力的剩余寿命联合概率密度函数图如图5所示。由图5可以看出Gumbel函数具有不对称的尾部结构，上尾高，下尾低，这说明在分布的上尾部变形和应力之间具有较强的相关性，在分布的下尾部两者之间则为渐进独立的。

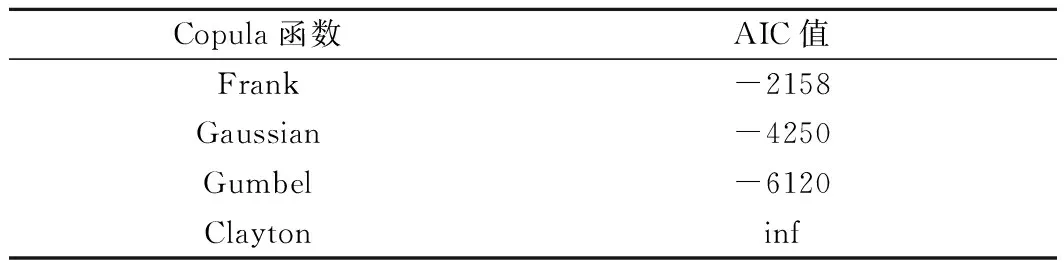
表3 4种Copula函数的AIC值

图5 二元Gumbel-Copula概率密度函数Fig.5 Density function of 2D Gumbel-Copula function

在选择好合适的Copula函数之后，由式(9)～(13)可得到不同运行年限的参数值，如表4所列。之后结合式(8)可以得到不同时刻的闸门剩余寿命概率密度函数，同时计算出基于应力退化的一元维纳过程预测的剩余寿命概率密度函数，将闸门概率密度函数最大值对应的时刻作为剩余寿命的预测值，如图6所示。由图6可以看出，随着闸门运行年限的增加，数据的增多，剩余寿命预测结果的分布范围越来越小，说明其预测结果的精确度越来越高，闸门发生失效的概率越来越高，闸门寿命减少，符合工程实际。

表4 不同运行年限的参数估计值

为了能够清晰地看出基于一元维纳过程和二元维纳过程预测闸门剩余寿命的变化趋势，将闸门实际寿命取SL 226-98《水利水电金属结构报废标准》中所规定的大型闸门折旧年限30 a[23]，将两种方法预测的闸门剩余寿命与真实剩余寿命相比较，如图7所示。从图7可以看出随着闸门运行年限的增加，基于二元维纳过程的闸门剩余寿命预测与真实寿命差距较小。

图6 闸门剩余寿命概率密度Fig.6 Probability density of remaining life of gate

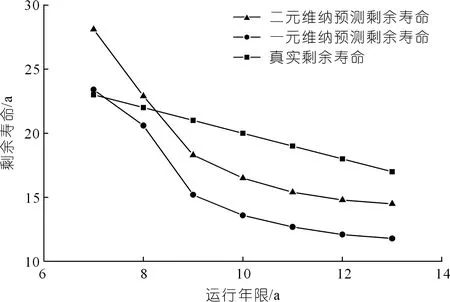
图7 不同方法预测寿命变化趋势Fig.7 Predicting trends of life expectancy by differet methods

为了客观比较两种方法预测闸门剩余寿命的精度，引入均方根误差(RMSE)和相对误差指标进行评价[24]。定义相对误差指标E：

(15)

式中：S为闸门剩余寿命预测值；T为闸门实际剩余寿命。

一元维纳过程和二元维纳过程预测结果的RMSE分别为4.72和3.46，这说明相较于单一指标，两个指标更能全面准确反映出闸门的寿命状态。不同预测方法的相对误差E如表5所列，由表5可以看出二元维纳过程的E<20%占比达到85.8%，而一元维纳过程E<20%仅占比28.6%，同时，基于二元维纳过程的E≥25%，占比为0，这说明基于二元维纳过程进行闸门寿命预测的方法可信度较高。

表5 不同预测方法的相对误差指标

通过对闸门剩余寿命预测可以指导闸门确定合理的维修时间，既避免了经常性维修造成的资金浪费，又避免了闸门因过久不维修而发生破坏，造成巨大的安全事故。基于随机过程预测闸门维修时间，可以根据闸门的重要性程度和维修的费用，确定闸门上的维修阈值ωm[25]。

本文假设闸门上的变形维修阈值为9.5 mm，应力维修阈值为143 MPa，当闸门到达维修阈值后，便进行一次全面大修，以延长闸门的剩余使用寿命。由于数据越多，预测越精确，因此根据13 a的数据，将维修阈值代入式(5)～(13)可以得到闸门的维修时间，如图8所示。由图8可知，维修阈值下剩余寿命还剩6 a，说明至少应在闸门运行19 a的时候进行一次大修，以确保闸门的运行安全。

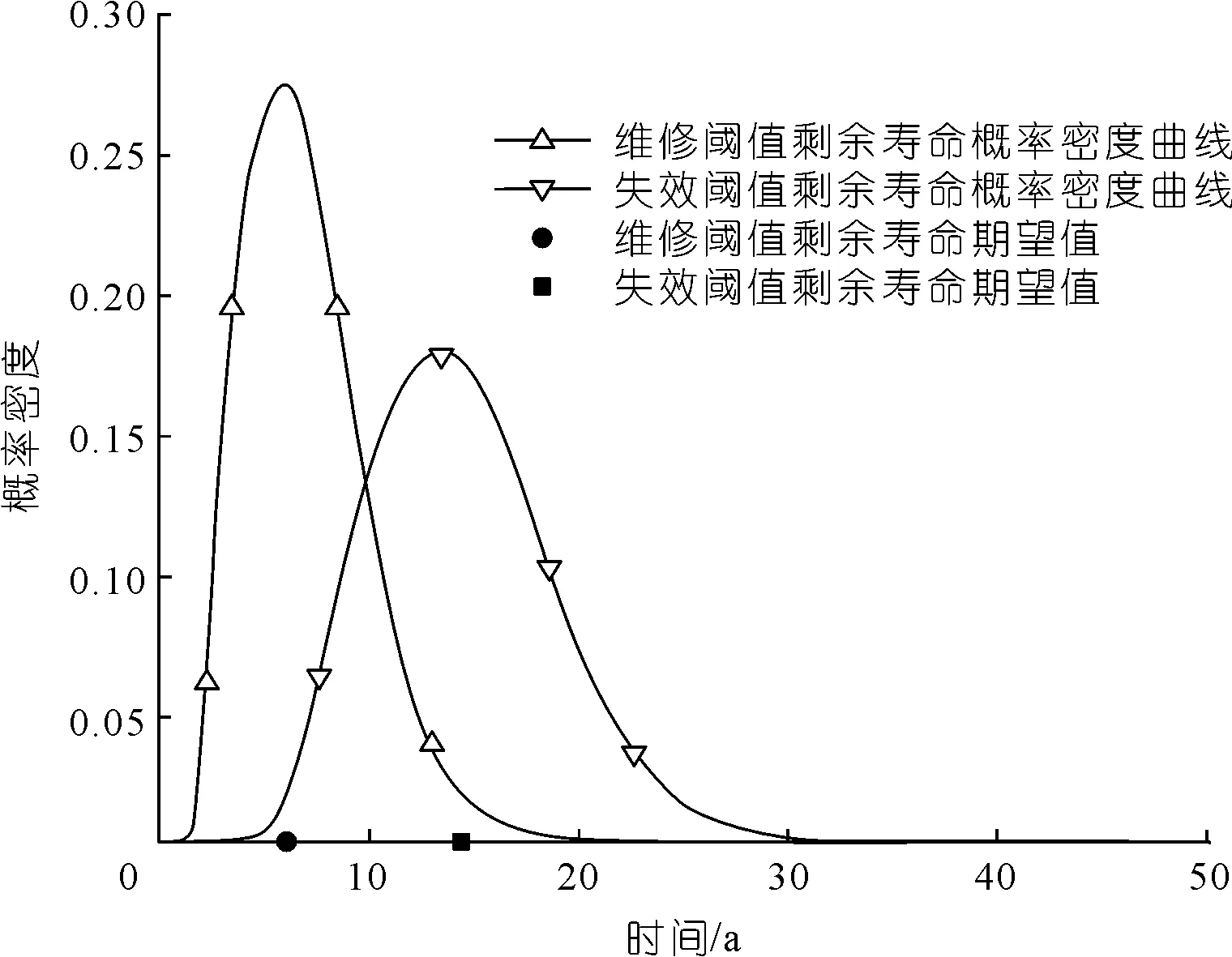
图8 闸门维修时间预测Fig.8 Forecast on gate maintenance time

4 结 论

(1) 利用二元维纳过程描述腐蚀情况下闸门退化过程，预测闸门剩余寿命的均方根误差RMSE为3.46，低于单一应力指标的RMSE值，说明用二元维纳过程方法来描述闸门退化过程具有合理性。

(2) 考虑到单一指标难以准确反映闸门的健康状态，利用变形和应力两个退化性能指标来预测闸门寿命，运用Gumbel函数描述其相关特性，预测寿命相对误差指标E≥25%占比为0，说明基于二元维纳过程的闸门剩余寿命预测具有较高的精度。

(3) 基于闸门剩余寿命预测结果，确定维修阈值，确定了闸门至少在运行19 a进行一次大修，以延长闸门使用寿命。同时，闸门上的失效形式众多，如何考虑更多的性能指标和维修过程对闸门的退化过程的影响，以达到更高的预测精度有待进一步研究。