基于改进纯跟踪的智能车路径跟随方法*
潘世举,李永乐,李子先,何滨兵,朱 愿,徐友春
(陆军军事交通学院,天津 300161)
前言
近年来,智能车辆迅速发展,逐步在矿区、港口、园区等相对封闭场景中进行商业化应用,并以辅助驾驶的方式参与人们的日常交通,具有广阔的前景。智能车系统涉及定位导航、环境感知、决策规划、运动控制等关键技术[1-3],其中路径跟随技术是通过控制转向系统改变横向运动状态,使车辆按照预设路线行驶,是运动控制的重要组成部分。
针对路径跟随技术,国内外学者进行了大量研究。根据是否需要建立车辆模型,可将现有研究分为无模型方法和有模型方法两大类。无模型的控制方法主要包括PID 方法[4]、模糊方法[5]、神经网络方法[6]等,这类方法主要依靠人类经验或大量训练样本,能够实现路径跟随功能,但参数选定过程复杂,或需要采集大量的高质量训练样本,训练耗时长,泛化能力较弱。有模型的控制方法主要包括Stanley方 法[7]、LQR方法[8]、MPC方法[9]和纯跟踪(pure pursuit,PP)方法[10-15]等,这类方法具备参数选定简单、跟随精度高的特点,但随着模型复杂度的提高,求解难度和运算成本升高,甚至无法满足实时性要求;另外,复杂车辆模型参数较多,无法对其进行充分的测量或辨识,也是导致复杂车辆模型在实际车辆控制应用中难于部署和控制精度达不到预期要求的重要原因。
上述方法中,PP 方法是以阿克曼转向模型为基础的控制方法,考虑了车辆的系统特性,控制参数少,可移植性和泛化能力较强,但前视距离的选择主要依靠人工经验,且跟随曲率较大的路径时精度较低,因此目前的研究主要集中在前视距离的选择和偏差反馈的利用。文献[10]中将车速作为选择前视距离的依据,车速越高,前视距离越长,并提出基于横向偏差的PI 转角补偿策略,提高了转弯精度,但跟随直线时的抗扰动能力较弱。文献[11]中将目标点的确定分为两步:第1 步利用速度和横向偏差得到路径上的目标点,以求快速消除偏差;第2 步利用横向偏差和曲率确定路径外的目标点,但存在直线超调问题。文献[12]中以横向偏差和航向偏差为基础,通过粒子群优化算法实时选定前视距离,提高直线行驶精度,但未考虑转弯工况。文献[13]中将PID 控制器和PP 控制器结合在一起,利用强化学习模型在两者之间进行权衡,但路径跟随精度较低。文献[14]中利用PP 方法得到基本转向控制量、深度强化学习得到校正控制量,两者结合提高了低速行驶条件下的路径跟随能力,但需采集训练样本和消耗大量训练时间。文献[15]中根据速度和路径弯度动态调节前视距离,实现农机的路径跟随控制,同时设置横向偏差阈值,当偏差大于阈值时对控制量进行放大处理,提高直线行驶的精度,但无法解决消除初始偏差过程中的超调问题。
针对以上问题,本文中提出一种基于改进纯跟踪(improved pure pursuit,I-PP)的路径跟随方法。首先建立纯跟踪模型,并分析纯跟踪模型在初始偏差条件下的控制效果;然后将航向偏差作为反馈量,对前轮转角控制量进行补偿,采用类模糊方法动态调节补偿权重,并根据期望转弯半径限制行驶速度;最后通过实车试验选定控制参数,并验证控制效果。结果表明,I-PP 方法能够快速消除初始偏差,提高行驶平稳性,并保持较低的运算耗时。
1 纯跟踪方法
1.1 纯跟踪模型
纯跟踪模型如图1 所示。图中:(x,y)为车辆后轴中心位置坐标;l为轴距;θ为航向角;v为行驶速度;Ld为前视距离;Pd为目标路径点;Rd为车辆的期望转弯半径;δd为前轮转角控制量;Od为车辆的转向中心;α为车辆与目标路径点的前视角度偏差。由阿克曼转向几何关系得前轮转角、轴距和转弯半径的关系:
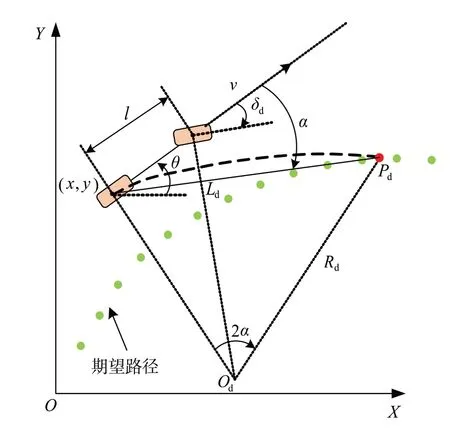
图1 PP方法示意图

由PP方法得前轮转角控制量为

1.2 控制效果分析
如图2(a)所示,智能车与期望路径存在初始偏差:横向偏差为le;航向偏差为θe;红色圆弧为由PP方法确定的行驶路线,与期望路径的夹角为θd。
随着时间的推移,车辆与期望路径的横向偏差逐渐减小,车辆行驶路线与期望路径之间始终存在夹角θd,由此导致在消除初始横向偏差后,车辆以航向偏差θe向期望路径另一侧行驶,横向偏差反向增大,从而导致车辆在期望路径附近振荡,如图2(b)所示。
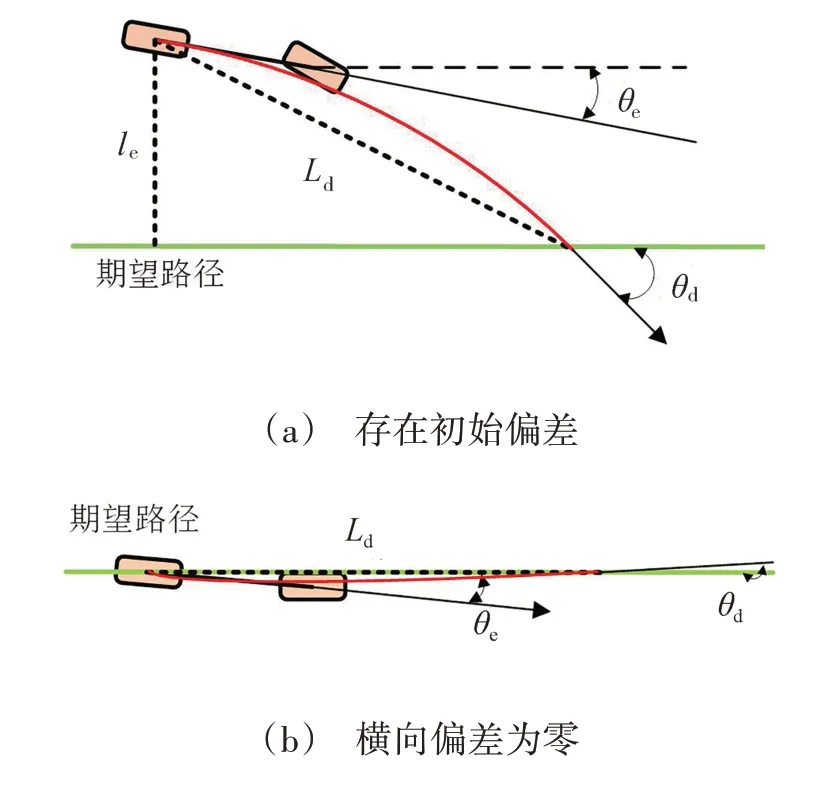
图2 PP方法跟随期望路径
综上所述,PP 方法具有约束条件少、计算量小和控制参数少等优点,但无法满足实际应用中对消除误差速度和较小振荡的要求。
2 改进纯跟踪方法
为实现快速消除偏差,同时保证振荡较小的目标,将航向偏差作为反馈量,对前轮转角控制量进行补偿,采用类模糊方法对补偿权重进行动态调节,并根据期望转弯半径限制行驶速度。
2.1 基于航向偏差的转角补偿
航向偏差反映车辆与期望路径之间的相对方向关系,是衡量路径跟随效果的重要指标之一。参考斯坦福大学提出的Stanley 方法,将航向偏差作为动态反馈变量对前轮转角进行补偿。

式中:δc为补偿后的前轮转角控制量;k为补偿权重。
2.2 类模糊的补偿权重
为快速消除路径跟随过程中的偏差,同时在靠近期望路径时减小振荡,根据横向偏差和航向偏差动态调节补偿权重k。当横向偏差le较大、航向偏差θe较小时,补偿权重k应为负大;当横向偏差le较小、航向偏差θe较小时,补偿权重k应为零;当横向偏差le较小、航向偏差θe较大时,补偿权重k应为正大。
根据上述权重调节规则,可实现补偿权重k随偏差动态变化,各变量论域如表1 所示,其中lmax、θmax、m分别为横向偏差极值、航向偏差极值、补偿权重极值,均为定值。
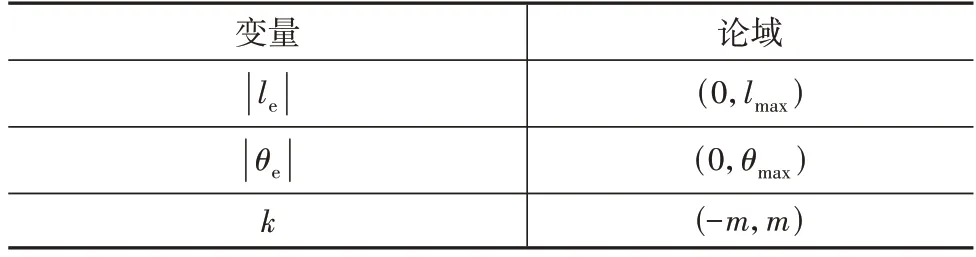
表1 变量论域
为减少计算量,采用类模糊方法,省略模糊化处理、模糊规则、解模糊等步骤,根据空间中不同线3点确定唯一平面的方法,确定横向偏差、航向偏差和补偿权重之间的关系。空间中不同线的3 点为(lmax,0,-m)、(0,0,0)、(0,θmax,m),则补偿权重k为
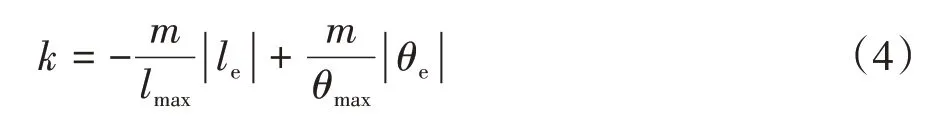
2.3 基于转弯半径的速度限制
为保证车辆行驶的平稳性,根据转弯半径对行驶速度进行限制:

式中:vc为速度控制量;vmax为目标行驶速度;Rc为期望转弯半径。
根据阿克曼转向模型,由控制量δc确定的转弯半径为Rc,即式(6)。

3 实车试验
3.1 试验平台
为验证本文方法在实车环境中的有效性,利用“军交木牛Ⅱ”平台进行实车试验,如图3(a)所示。该平台为课题组自行设计研制的无人载货运输智能车,搭载云台相机、激光雷达、超声波雷达、惯性导航等高性能传感器,以及工控机、DSRC、远距离电台等设备,能够实现超视距操控、自主行驶、编队运输等功能,软件架构如图3(b)所示。在校园内部的平坦道路开展试验,路面为干燥且较新的沥青路面,附着系数在0.8~1.0 之间。试验平台参数和部分控制参数如表2所示。

表2 车辆参数和部分控制参数
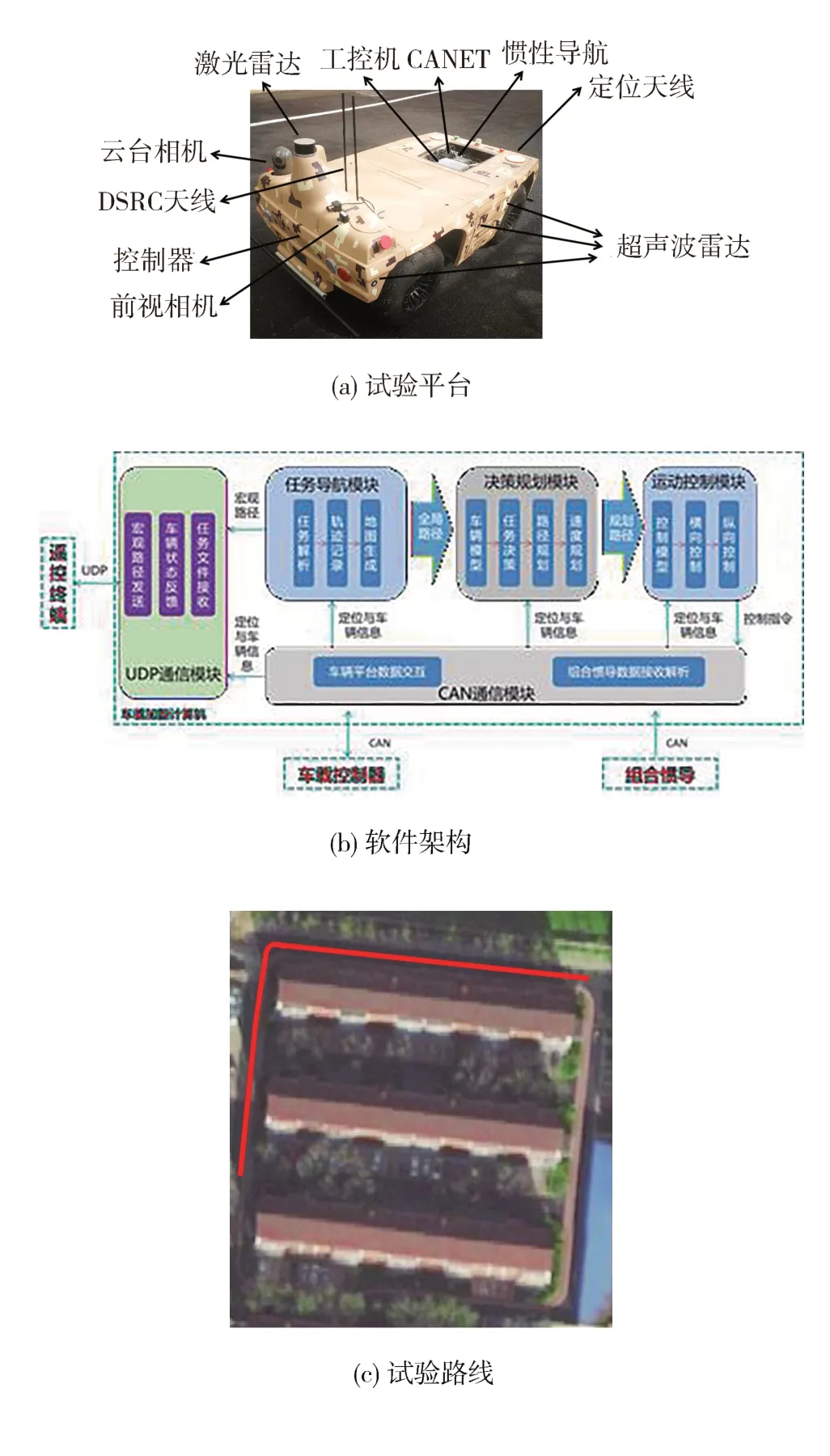
图3 “军交木牛Ⅱ”试验平台
3.2 前视距离选定试验
为选定合适的前视距离Ld,分别设定为2、3、4 m,初始横向偏差为-1 m,初始航向偏差为零,vmax为2 km/h,期望路径为直线,采用PP 方法进行路径跟随试验,结果如图4所示。
图4(a)为横向偏差变化曲线,前视距离为2、3 m时的超调量分别为0.13、0.07 m,前视距离为4 m 时无超调,但行驶后期的路径跟随偏差较大,路径跟随精度较低。图4(b)为航向偏差变化曲线,随着前视距离的增大,航向偏差极值减小,但收敛速度基本一致。图4(c)为转角控制量变化曲线,为方便数据分析,将转角控制量进行归一化处理,由图可知,前视距离越大,控制量变化越平稳。
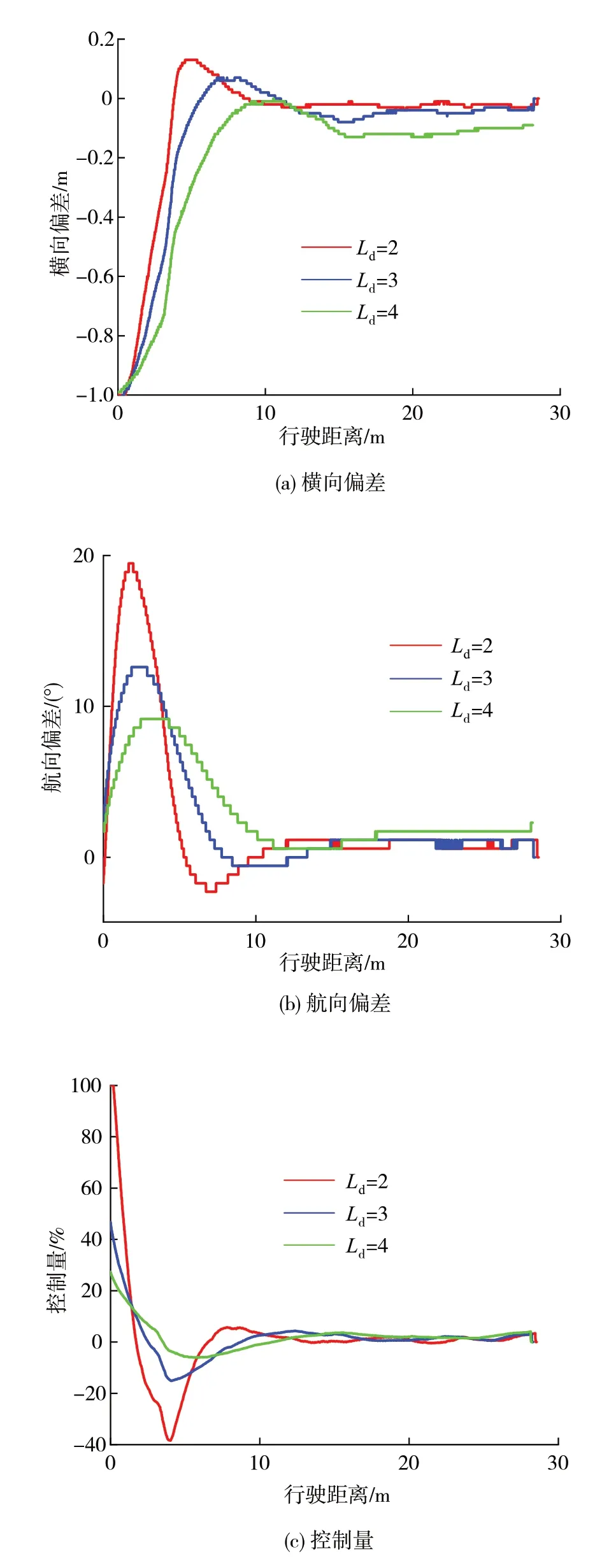
图4 不同前视距离的试验结果
综上,为保持较高的路径跟随精度,同时保证控制量的平稳变化,选定3 m为前视距离。
3.3 m值选定试验
为选定I-PP 方法的权重极值m,分别设定为2、4、6,Ld=3,初始横向偏差为-1 m,初始航向偏差为零,vmax为2 km/h,期望路径为直线,以PP 方法为对照组进行试验,结果如图5所示。
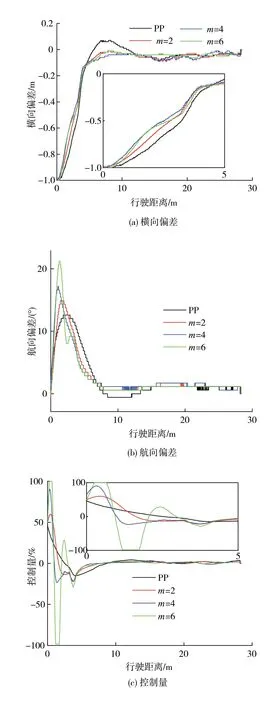
图5 不同m值的试验结果
图5(a)为横向偏差变化曲线,PP 方法的超调量为0.07 m,m为2、4、6 时无超调现象,随着m值增大,偏差消除速度加快。图5(b)为航向偏差变化曲线,PP 方法的航向偏差极值最小,但存在超调现象;随着m值的增大,航线偏差极值逐渐增大,且变化越剧烈。由图5(c)可知,在消除初始偏差的过程中,PP方法的控制量变化平稳,m值越大,控制量的变化越剧烈。
综上,为快速消除偏差,保证转角控制量平稳变化,选定m值为4。
3.4 不同初始偏差试验
为验证所提方法在不同初始偏差条件下的路径跟随效果,控制参数不变,vmax为2 km/h,期望路径为直线,以PP方法为对照组进行试验。
3.4.1 不同初始横向偏差
初始航向偏差为零,初始横向偏差分别为-0.5、1.5 m,结果如图6 所示。图6(a)中,PP 方法在不同初始横向偏差下的超调量分别为0.03、0.14 m,存在小幅振荡;I-PP 方法的偏差收敛速度更快,且不存在超调振荡现象。图6(b)中,在初始阶段,I-PP方法的控制量远大于PP 方法,初始偏差的消除速度更快,当偏差较小时,减小控制量,避免超调振荡。
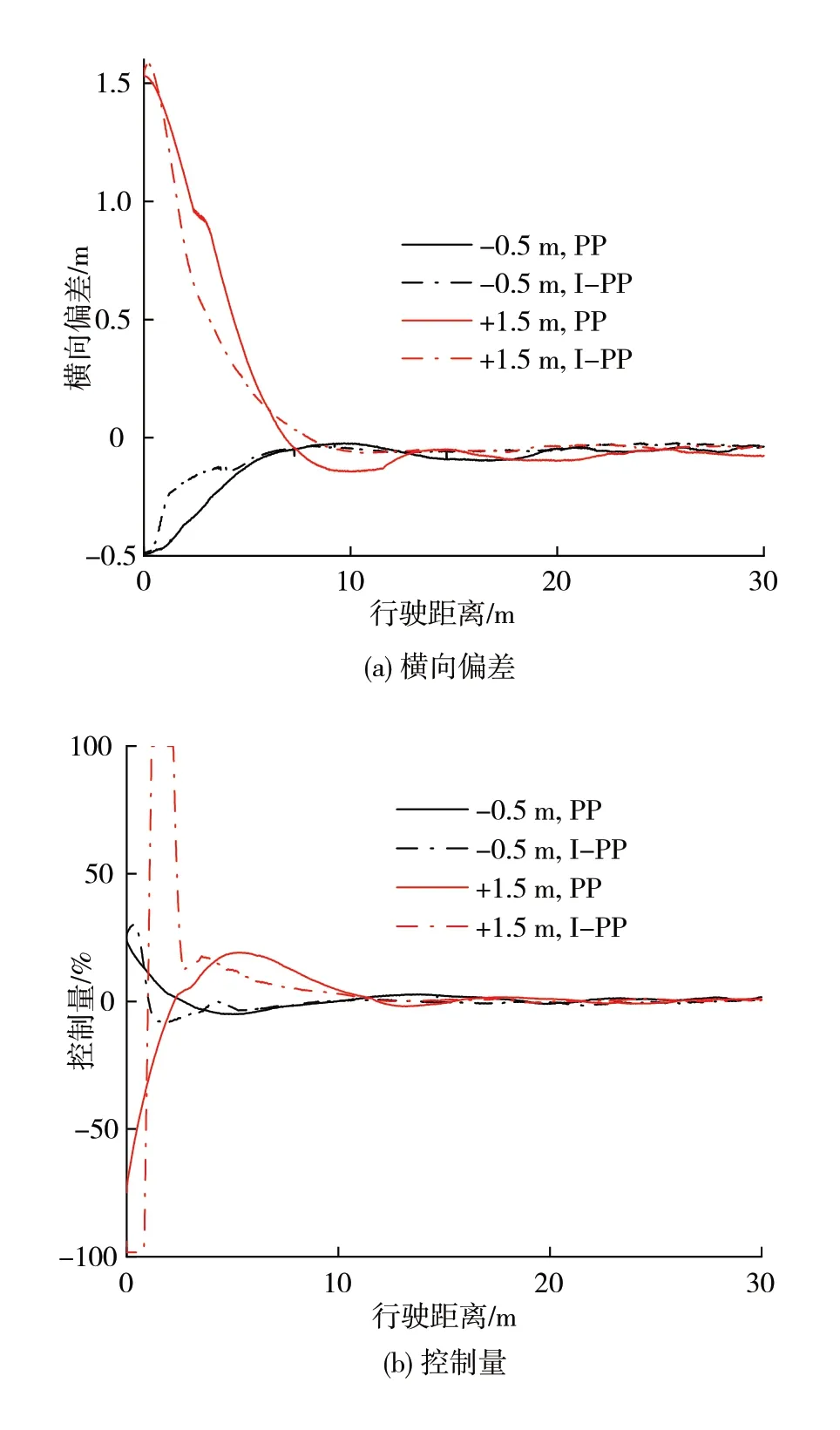
图6 不同初始横向偏差的试验结果
结果表明,I-PP 方法能够适应不同初始横向偏差的工况。
3.4.2 不同初始航向偏差
初始横向偏差为-1.5 m,初始航向偏差分别为-45°、-10°、10°、45°,结果如图7所示。
图7(a)中,在上述初始航向偏差下,PP 方法的超调量为0.08、0.04、0.05、0.32 m,I-PP 方法无超调,初始横向偏差消除速度更快。
图7(b)中,当初始航向偏差为-45°、-10°、10°时,I-PP 方法下的偏差极值大于PP 方法;当初始航向偏差为45°时,PP 方法下的偏差极值大于I-PP 方法。I-PP 方法下的航向偏差向零收敛的速度更快,且无超调振荡;PP 方法下的航向偏差变化更平稳,但存在超调振荡。
图7(c)中,I-PP方法的控制量极值远大于PP方法,在短时间内迅速变化,加快初始偏差的消除速度,同时避免超调振荡。
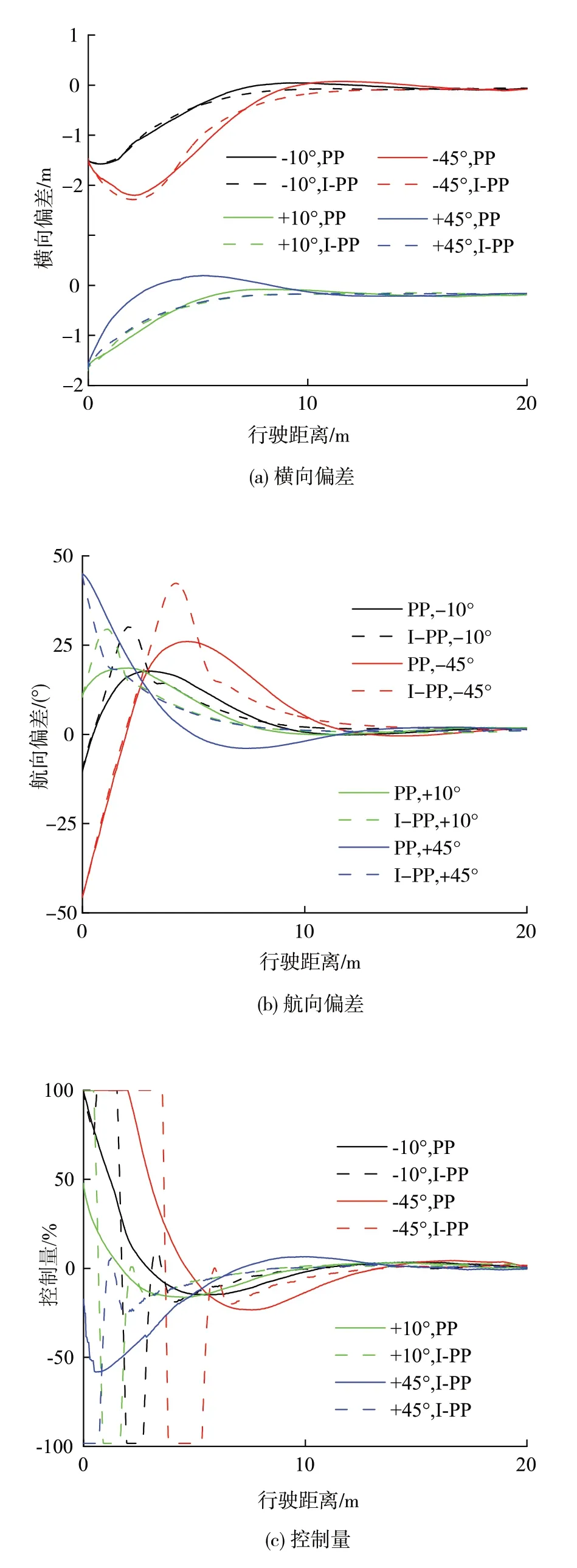
图7 不同初始航向偏差的试验结果
结果表明,所提I-PP 方法能够在不同初始横向偏差和不同航向偏差的工况下,具有较好的路径跟随效果。
3.5 不同速度试验
为验证所提方法在不同目标行驶速度条件下的路径跟随效果,控制参数保持不变,初始横向偏差为1.5 m,初始航向偏差为30°,vmax分别为5、10 km/h,期望路径为直线,以PP 方法为对照组进行试验,结果如图8所示。
由图8(a)可得,5 和10 km/h 的工况下,PP 方法的超调量分别为0.14、0.09 m,偏差消除速度较慢;I-PP 方法的超调量分别为0.02、0.004 m,初始偏差消除速度较快,且无明显超调振荡。由图8(b)可得,PP 方法下的航向变化更平稳,且航向偏差极值小于I-PP 方法。由图8(c)可得,为快速消除初始偏差,I-PP 方法下的控制量极值更大。图8(d)可得,在初始阶段,I-PP 方法的行驶速度小于PP 方法,主要原因是:I-PP 方法转角控制量较大,为保证平稳性,根据转弯半径对行驶速度进行了限制。由图8(e)可得,PP 方法的横摆角速度极值分别为94、100(°)/s,I-PP 方法为64、73(°)/s,在消除初始偏差的过程中,I-PP方法的行驶状态更平稳。
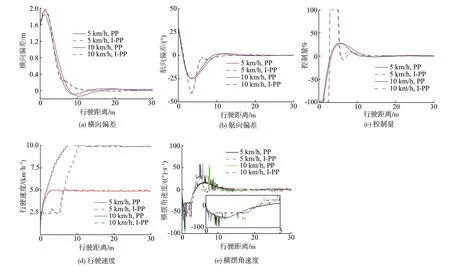
图8 不同速度的试验结果
结果表明,所提I-PP 方法能够在不同目标行驶速度条件下,根据期望转弯半径调节行驶速度,在快速消除初始偏差的同时,提高行驶平稳性,路径跟随效果较好。
3.6 不同期望路径试验
上述试验中的期望路径均为直线路径,期望航向为定值。为验证所提方法对转弯路径的跟随效果,控制参数不变,初始横向偏差为1.5 m,航向偏差分别为-30°、30°,以PP 方法为对照组进行试验,结果如图9所示。
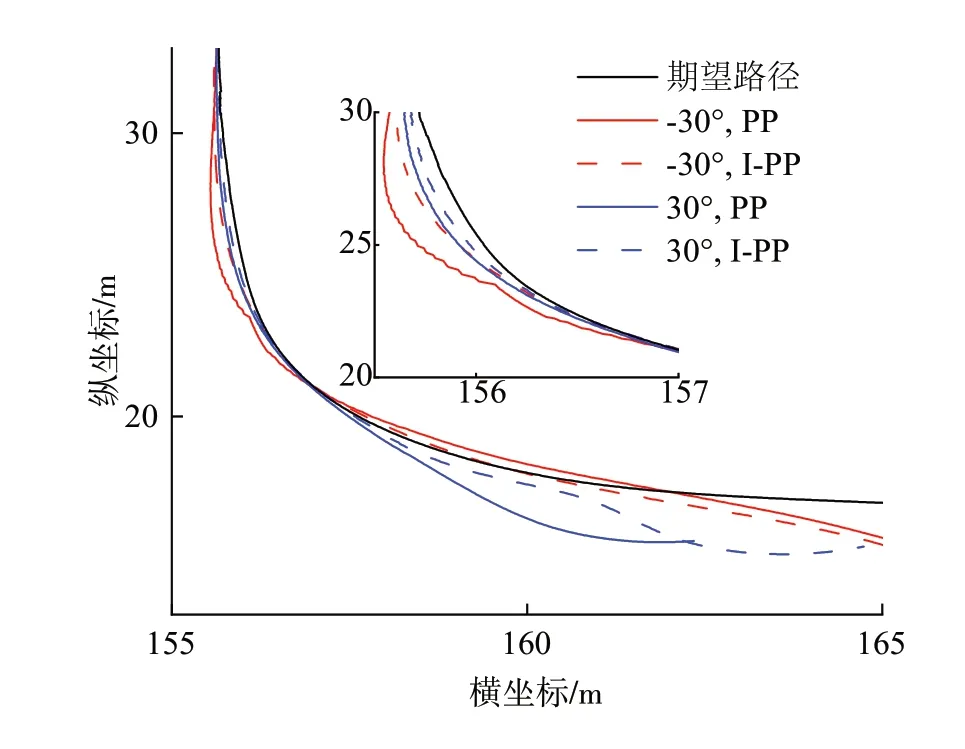
图9 期望路径与行驶路径
由图9 可得,当初始航向偏差为-30°时,两种方法下的行驶路径向期望路径靠拢,但PP方法的超调量大于I-PP 方法。当初始航向偏差为30°时,PP 方法向期望路径靠拢的更平滑,I-PP 方法向期望路径靠拢的速度更快。在消除初始偏差后,与PP方法相比,I-PP 方法下的行驶路径与期望路径的偏差较小,路径跟随效果较好。
在干燥且较新的平坦沥青路面选定I-PP 方法的控制参数,与PP 方法相比,I-PP 方法的初始偏差消除速度和行驶稳定性有所提高。路面附着系数发生变化时,路径跟随精度降低,横向偏差和航向偏差增大。I-PP 方法采用基于航向偏差的转角补偿策略,补偿权重与横向偏差、航向偏差相关,因此横向偏差和航向偏差变化时,转角控制量也随之变化,保持较高的路径跟随精度。
当路面的侧倾角度、俯仰角度和附着系数等状态发生变化时,车辆的质心和转向特性等随之发生变化,阿克曼转向模型与车辆实际运动状态的匹配程度降低,为保持较高的路径跟随精度,应适当减小前视距离、增大m值。随着前视距离的减小和m值的增大,I-PP 方法对偏差的响应更加敏感,转角控制量变化更剧烈,行驶稳定性下降。
3.7 不同控制方法试验
为验证所提路径跟随方法的优势,控制参数不变,初始横向偏差为1.5 m,初始航向偏差为30°,vmax为5 km/h,期望路径为直线,以LQR 方法和MPC 方法为对照组进行试验,结果如图10所示。
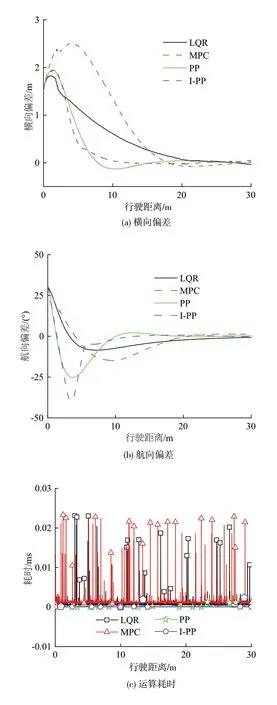
图10 不同控制方法的试验结果
由图10(a)的横向偏差变化曲线可得,与PP 方法相比,LQR 方法和MPC 方法能够消除初始偏差,横向偏差变化更平稳且无超调现象,但偏差消除速度较慢。由图10(b)可知,I-PP 方法的航向偏差极值最大,LQR 方法的最小;与其他3 种方向相比,IPP 方法的航向偏差收敛速度更快,且无超调现象。由图10(c)可得,MPC、LQR、PP、I-PP 方法的平均耗时分别为0.015、0.008、0.007、0.007 ms,MPC 方法和LQR 方法的部分耗时过长,在PP 方法的基础上,引入转角动态补偿方法对运算耗时影响不大。
结果表明,I-PP 方法的初始偏差消除速度更快,与MPC 方法和LQR 方法相比具有运算耗时少的优势。
4 结论
本文中提出一种基于改进纯跟踪的路径跟随方法。以纯跟踪方法为基础,以航向偏差为反馈变量对前轮转角进行补偿;以横向偏差和航向偏差为输入,采用类模糊的方法动态调节补偿权重;根据期望转弯半径限制行驶速度,提高行驶平稳性。试验结果表明,在初始偏差、目标行驶速度和期望路径不同的工况下,所提方法能够实现偏差的快速收敛,改善路径跟随效果,提高行驶平稳性,同时保持较低运算耗时。

