地铁钢弹簧浮置板轨道结构振动传递特性分析
汪杰


[摘要]为分析钢弹簧浮置板轨道结构在不同减振参数下的振动传递特性,将钢弹簧浮置板轨道系统简化为3层叠合梁的计算模型分析振动系统的振动传递系数,根据多参数下的振动传递系数曲线来分析钢弹簧浮置板轨道振动传递特性。结果表明:不同刚度下的振动传递系数曲线在频率分布上存在频率敏感性,离散刚度比为0.1~0.4时,振动传递系数的频率敏感区间分别为15~32 Hz、20~32 Hz、22~32 Hz及25~32 Hz;考虑全频域激振力作用下,建议扣件垂向阻尼值取为93.75×103~125×103 N·s/m,钢弹簧垂向阻尼取为18.75×103~37.5×103 N·s/m,并增大浮置板的单位质量,可使传递到下部基础的振动响应较小。
[关键词]钢弹簧浮置板轨道; 振动传递系数; 传递特性; 频率敏感性; 振动响应; 敏感区间
[中国分类号]U213.2+1 [文献标志码]A
0引言
随着城市地铁网建设的快速发展,由地铁运营引起的环境噪声和振动问题日趋严重[1-2]。为进一步控制其影响,在地铁建设中采用多种减振型轨道结构,如弹性支承块式轨道、埋入式轨道、浮置板轨道等[3-4]。其中,钢弹簧浮置板轨道相比,具有减振效果显著、维修工作量少等优点[5-6],但钢弹簧浮置板轨道造价高昂,在工程设计之初,需结合轨道结构设计特点对其振动传递特性进行分析,来确定钢弹簧浮置板轨道减振参数的合理取值,否则难以达到预期减振效果,造成一定的经济损失。因此,针对钢弹簧浮置板轨道结构的振动传递特性进行分析研究,对实际工程应用具有重要的理论价值和现实意义。本文将钢弹簧浮置板轨道结构简化为3层叠合梁模型,根据简谐荷载作用下钢弹簧浮置板轨道系统的振动微分方程,求解钢弹簧浮置板振动系统的振动传递系数,通过多参数下振动传递系数曲线分析钢弹簧浮置板轨道结构的振动传递特性,并给出相关减振参数的建议取值。
1振动传递系数求解
钢弹簧浮置板轨道结构形式见图1。
简谐激振力作用下钢弹簧浮置板轨道结构的3层叠合梁计算模型如图2所示。钢轨简化为离散点支承的无限长梁,具有抗弯刚度EI和分布质量m1;扣件和钢弹簧简化为弹簧—阻尼单元,支承间距分别为0.625、1.25 m,离散刚度(支承刚度与支承间距比值)分别为k1和k2,離散阻尼(阻尼与支承间距比值)分别为c1和c2;不考虑浮置板和刚性基础的抗弯刚度,将其视为弹性支承刚性梁,浮置板计算长度为25 m,浮置板和刚性基础分布质量分别为m2和m3;将地基础视为均匀分布的弹簧—阻尼单元,支承刚度和阻尼分别为k3和c3。则钢弹簧浮置板轨道系统的振动微分方程见式(1)。
EI4z1(x,t)x4+m12z1(x,t)t2+
c1(z1(x,t)t-z2(x,t)t)+k1z1(x,t)-k1z2(x,t)=Fejωtm22z2(x,t)t2+c2(z2(x,t)t-z3(x,t)t)+
k2(z2(x,t)-z3(x,t))=(1)c1(z1(x,t)t-z2(x,t)t)+k1(z1(x,t)-z2(x,t))m32z3(x,t)t2+c3z3(x,t)t+k3z3(x,t)=
c2(z2(x,t)t-z3(x,t)t)+k2(z2(x,t)-z3(x,t))令:zi(x,t)=Zi(x)·ejωt(i =1~3),则zi(x,t)t=jω·Zi(x)·ejωt,2zi(x,t)t2=-ω2·Zi(x)·ejωt,
4zi(x,t)x4=Zi(4)(x)·ejωt,代入式(1)中可得式(2):
EI·Z(4)1(x)+(-m1ω2+jωc1+k1)·Z1(x)-
(jωc1+k1)·Z1(x)=F[-m2ω2+jω(c1+c2)+
k1+k2]·Z2(x)-(jωc1+k1)·Z1(x)-(2)(jωc2+k2)·Z3(x)=0[-m3ω2+jω(c2+c3)+k2+k3]·Z3(x)-
(jωc2+k2)·Z2(x)=0
由式(2)得钢弹簧浮置板轨道系统的振动传递系数式(3):
β=|G+HjM+Nj|=(GM+HN)2+(HM-GN)2M2+N2
式中,G=k1k2-c1c2ω2,H=ω(c1k2+c2k1),
M=m2m3ω4-ω2[m2(k2+k3)+m3(k1+k2)+c1(c2+c3)+c2c3]+k1(k2+k3)+k2k3(3)
N=ω[c1(k2+k3)+c2(k1+k3)+c3(k1+k2)]-ω3[m2(c2+c3)+m3(c1+c2)]
式中:ω为简谐荷载的激振频率。
2振动传递系数曲线分析
钢弹簧浮置板轨道结构中,钢轨采用CHN60轨,其分布质量m1=60 kg/m,浮置板分布质量m2与浮置板密度和尺寸有关,刚性基础分布质量m3=3000 kg/m;扣件采用DTⅥ2型扣件,其静刚度为(20~40)×106 N/m,则k1=(32~64)×106 N/m,地基础支承刚度为k3=26×107 N/m;扣件垂向离散阻尼取值为c1=(25~300)×103 N·s/m,钢弹簧垂向离散阻尼取值为c2=(5~150)×103 N·s/m,地基础阻尼为c3=25×104 N·s/m。
2.1振动传递系数随刚度变化分析
分布质量和阻尼值一定时,考虑扣件垂向刚度和刚弹簧垂向刚度变化对振动传递系数随频率分布的影响,令k2=nk1(n为离散刚度比),振动传递系数曲线如图3所示。
由图3可知:在振动系统固有频率处,振动传递系数达到峰值,随着扣件垂向离散刚度和刚度比的增大,振动传递系数的峰值也随之增大;随着离散刚度比(钢弹簧垂向离散刚度)的增大,振动系统的振动传递系数也随之增大;扣件垂向刚度和钢弹簧垂向刚度的增大将削弱振动系统二阶固有频率的影响,振动传递系数的峰值集中在一阶固有频率处;激振频率大于80 Hz时,振动传递系数值趋于稳定,即扣件和钢弹簧刚度取值对振动传递系数大小基本没有影响。
不同扣件及钢弹簧垂向离散刚度下振动传递系数曲线在频域上某一频率区间的分布存在频率敏感性,截取某一敏感频段范围内振动传递系数曲线如图4所示。
离散刚度比为0.1~0.4时,振动传递系数的频率敏感区间分别为15~32 Hz、20~32 Hz、22~32 Hz及25~32 Hz。由图4可知:激振频率不在振动传递系数频率敏感区间时,随着扣件垂向离散刚度增大,振动传递系数也随之增大;激振频率处在振动传递系数频率敏感区间时,不同扣件垂向离散刚度呈现出了频率敏感性;随着离散刚度比的增大,振动传递系数的频率敏感性逐渐被削弱。若在全频域或非频率敏感区间激振力作用下,选择较小的扣件和钢弹簧垂向刚度时,可使振动传递系数取得较小值,传递到下部基础的振动响应较小;在频率敏感区间激振力作用下,可根据扣件垂向刚度的频率敏感性选择合理的刚度值,匹配较小的钢弹簧垂向刚度时,可使传递到下部基础的振动响应较小。
2.2振动传递系数随阻尼变化分析
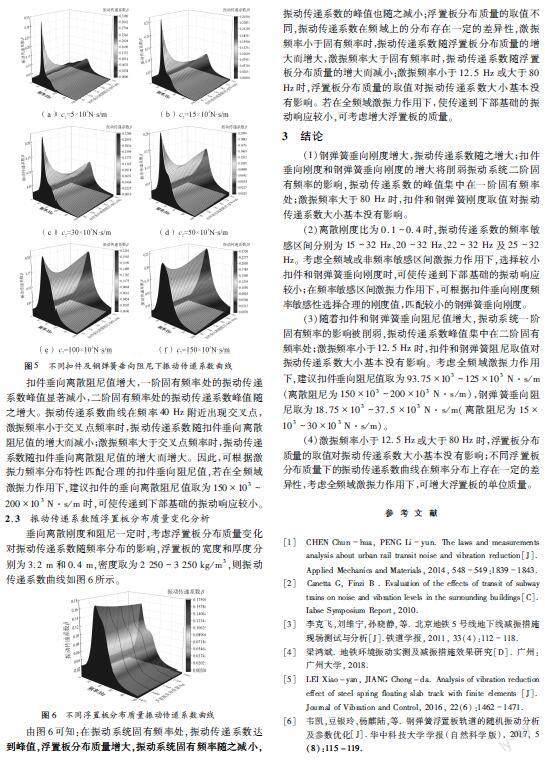
垂向刚度和分布质量一定时,考虑扣件垂向离散阻尼和刚弹簧垂向离散阻尼变化对振动传递系数随频率分布的影响,则振动传递系数曲线如图5所示。
由图5可知:在振动系统固有频率处,振动传递系数达到峰值,随着扣件和钢弹簧的垂向离散阻尼值的增大,振动系统一阶固有频率的影响将被削弱,振动传递系数的峰值集中在二阶固有频率处;激振频率小于12.5 Hz时,扣件和钢弹簧的阻尼取值对振动传递系数大小基本没有影响。
扣件垂向离散阻尼值大于75×103 N·s/m时,振动传递系数随着钢弹簧垂向离散阻尼值的增大而增大,钢弹簧垂向离散阻尼值大于30×103 N·s/m时,振动传递系数将明显增大。扣件垂向离散阻尼值小于75×103 N·s/m时,一阶固有频率处的振动传递系数峰值随着钢弹簧离散阻尼值的增大先减小后增大,二阶固有频率处的振动传递系数值峰值随之增大;钢弹簧垂向离散阻尼值大于30×103 N·s/m时,将明显增大二阶固有频率处振动传递系数的峰值;钢弹簧垂向离散阻尼值小于15×103 N·s/m时,将明显增大一阶固有频率处振动传递系数的峰值。因此,建议钢弹簧垂向离散阻尼值取为15×103~30×103 N·s/m。
扣件垂向离散阻尼值增大,一阶固有频率处的振动传递系数峰值显著减小,二阶固有频率处的振动传递系数峰值随之增大。振动传递系数曲线在频率40 Hz附近出现交叉点,激振频率小于交叉点频率时,振动传递系数随扣件垂向离散阻尼值的增大而减小;激振频率大于交叉点频率时,振动传递系数随扣件垂向离散阻尼值的增大而增大。因此,可根据激振力频率分布特性匹配合理的扣件垂向阻尼值,若在全频域激振力作用下,建议扣件的垂向离散阻尼值取为150×103~200×103 N·s/m时,可使传递到下部基础的振动响应较小。
2.3振动传递系数随浮置板分布质量变化分析
垂向离散刚度和阻尼一定时,考虑浮置板分布质量变化对振动传递系数随频率分布的影响,浮置板的宽度和厚度分别为3.2 m和0.4 m,密度取为2 250~3 250 kg/m3,则振动传递系数曲线如图6所示。
由图6可知:在振动系统固有频率处,振动传递系数达到峰值,浮置板分布质量增大,振动系统固有频率随之减小,振动传递系数的峰值也随之减小;浮置板分布质量的取值不同,振动传递系数在频域上的分布存在一定的差异性,激振频率小于固有频率时,振动传递系数随浮置板分布质量的增大而增大,激振频率大于固有频率时,振动传递系数随浮置板分布质量的增大而减小;激振频率小于12.5 Hz或大于80 Hz时,浮置板分布质量的取值对振动传递系数大小基本没有影响。若在全频域激振力作用下,使传递到下部基础的振动响应较小,可考虑增大浮置板的质量。
3结论
(1)钢弹簧垂向刚度增大,振动传递系数随之增大;扣件垂向刚度和钢弹簧垂向刚度的增大将削弱振动系统二阶固有频率的影响,振动传递系数的峰值集中在一阶固有频率处;激振频率大于80 Hz时,扣件和钢弹簧刚度取值对振动传递系数大小基本没有影响。
(2)离散刚度比为0.1~0.4時,振动传递系数的频率敏感区间分别为15~32 Hz、20~32 Hz、22~32 Hz及25~32 Hz。考虑全频域或非频率敏感区间激振力作用下,选择较小扣件和钢弹簧垂向刚度时,可使传递到下部基础的振动响应较小;在频率敏感区间激振力作用下,可根据扣件垂向刚度频率敏感性选择合理的刚度值,匹配较小的钢弹簧垂向刚度。
(3)随着扣件和钢弹簧垂向阻尼值增大,振动系统一阶固有频率的影响被削弱,振动传递系数峰值集中在二阶固有频率处;激振频率小于12.5 Hz时,扣件和钢弹簧阻尼取值对振动传递系数大小基本没有影响。考虑全频域激振力作用下,建议扣件垂向阻尼值取为93.75×103~125×103 N·s/m(离散阻尼为150×103~200×103 N·s/m),钢弹簧垂向阻尼取为18.75×103~37.5×103 N·s/m(离散阻尼为15×103~30×103 N·s/m)。
(4)激振频率小于12.5 Hz或大于80 Hz时,浮置板分布质量的取值对振动传递系数大小基本没有影响;不同浮置板分布质量下的振动传递系数曲线在频率分布上存在一定的差异性,考虑全频域激振力作用下,可增大浮置板的单位质量。
参考文献
[1]CHEN Chun-hua, PENG Li-yun. The laws and measurements analysis about urban rail transit noise and vibration reduction[J]. Applied Mechanics and Materials, 2014, 548-549:1839-1843.
[2]Canetta G, Finzi B . Evaluation of the effects of transit of subway trains on noise and vibration levels in the surrounding buildings[C]. Iabse Symposium Report, 2010.
[3]李克飞,刘维宁,孙晓静,等. 北京地铁5号线地下线减振措施现场测试与分析[J].铁道学报, 2011, 33(4):112-118.
[4]梁鸿斌. 地铁环境振动实测及减振措施效果研究[D]. 广州:广州大学, 2018.
[5]LEI Xiao-yan, JIANG Chong-da. Analysis of vibration reduction effect of steel spring floating slab track with finite elements [J]. Journal of Vibration and Control, 2016, 22(6):1462-1471.
[6]韦凯,豆银玲,杨麒陆,等. 钢弹簧浮置板轨道的随机振动分析及参数优化[J].华中科技大学学报(自然科学版), 2017, 5(8):115-119.

