新型油水相渗数学模型的建立及应用

李婧，范晖，刘春茹，杨芳

(中国石油 吐哈油田分公司a.勘探开发研究院；b.三塘湖采油管理区；c.鄯善采油管理区，新疆 哈密 839009)

油水两相相对渗透率是研究油水两相渗流的基础参数，也是进行油田开发设计、动态分析以及数值模拟的重要参数[1-3]。研究油水相渗曲线应用较多的是Willhite 数学模型[4-7]，但利用该数学模型拟合实验数据时，含水饱和度越低，油相相对渗透率拟合误差越大；水相整体误差相对较小，但随含水饱和度增大，也出现水相相对渗透率拟合误差也增大的现象[8]。针对此现象，文献［8］提出油相和水相指数并非常数，并对Willhite 数学模型进行了改进，使得相对渗透率拟合精度得到很大的提高，但改进后的水相相渗关系式在拟合渗透率差异较大的多产层油井相渗曲线时，不同层水相相渗曲线的待定参数差异较大，利用算术平均法确定的油藏标准水相相渗曲线偏离层数较少的高渗主力产层，而偏向层数较多的低渗透非主力产层。为此，本文提出了一种新型Willhite数学模型。

1 新模型的建立

文献［8］中提出了一种改进Willhite数学模型：

选取红台油田红台2301 井岩样17、岩样18 和岩样43，其空气渗透率分别为0.497 mD、0.306 mD 和1.730 mD，有效渗透率分别为0.256 mD、0.146 mD 和0.412 mD。在应用上述改进Willhite 数学模型时，发现水相相渗曲线呈现弓背式形态时(图1)，拟合待定参数与凹型形态的参数差异较大[9]。如岩样43 的拟合参数m是其他岩样的4 倍多，c的绝对值变大，数值变小，d远小于其他岩样，这对利用岩样拟合参数平均值来确定油藏标准油水相渗曲线将产生很大的影响(表1)。因此，需要对(2)式进行改进。

图1 红台2301井油水相渗曲线Fig.1.Relative permeability curves of oil/water phase in Well HT2301

表1 红台2301井按文献［8］中改进水相相渗曲线拟合结果Table 1.Fitting results of the improved relative permeability curves of water phase in Well HT2301 according to Ref.[8]

由于Willhite 提出的幂函数模型在水相指数m为常数时，随归一化含水饱和度的增大单调递增，而(2)式只对比较敏感的幂指数进行了改变，未对幂函数底数结构进行改变，在拟合弓背式水相相渗曲线时，容易出现待定参数m和c过大、d过小的现象。若对Willhite 提出的水相相渗关系式的幂指数和底数同时进行结构改进，即确保归一化含水饱和度为0 时，水相相对渗透率为0，归一化含水饱和度为1时，水相相对渗透率为残余油饱和度下的水相相对渗透率的条件成立，固定(2)式幂指数中归一化含水饱和度的指数为1，d前移到底数的变量中，得到如下数学模型：

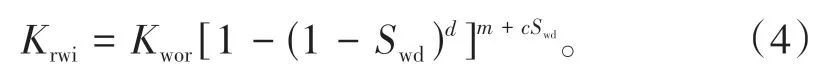
从拟合相关系数来看，(4)式比(2)式的拟合效果要好，3 个岩样的拟合相关系数均大于0.986 6。从红台2301 井不同岩样拟合参数来看，(4)式的m、c和d变化区间比(2)式小，相对较集中(表2)。

表2 红台2301井新型油水相渗曲线拟合结果Table 2.Fitting results of the new relative permeability curves of oil/water phase in Well HT2301

2 新模型的求解

由于束缚水饱和度下的油相相对渗透率一般为1，令y0=lnKro/ln(1 -Swd)，x0=，a0=n，a1=b，则(1)式转化为

对于(4)式，令y1=lnKrwi，x1=ln[1 -(1 -Swd)d]，x2=Swdln[1 -(1 -Swd)d]，a2=lnKwor，a3=m，a4=c，则(4)式转化为

利用(5)式和(6)式，对红台2301井3块岩样相对渗透率和归一化含水饱和度进行拟合，再计算拟合参数的算术平均值，得到n为3.912 2，b为-1.924 9，k为5.170 1，m为1.362 1，c为0.941 1，d为1.295 7，这些参数值作为红台2301井油水相渗曲线的特征值[10]；其次，利用空气渗透率加权平均确定出3块岩样的束缚水饱和度为0.420 9，残余油饱和度为0.223 5；最后，将拟合参数的算术平均值、束缚水饱和度和残余油饱和度代入(1)式和(4)式，得到红台2301井标准油水相渗曲线(图2)。

图2 红台2301井标准油水相渗曲线Fig.2.Standard relative permeability curves of oil/water phase in Well HT2301

同理，利用(1)式和(2)式，也可得到红台2301 井的标准油水相渗曲线。很明显，本文改进模型确定的标准油水相渗曲线与岩样43 的油水相渗曲线相似，而根据文献［8］改进模型确定的标准油水相渗曲线在中—高含水期与岩样17和岩样18的油水相渗曲线相似，在高含水期与岩样43 的油水相渗曲线相似。这对于多层生产的红台2301 井而言，物性好的岩样43代表主力油层，物性较差的岩样17 和岩样18 代表非主力油层，因此，按照试井解释[11]，油井的油水两相渗流特征应与主力油层的油水两相渗流特征相近，即利用(1)式和(4)式确定的标准油水相渗曲线，更能反映红台2301井的油水两相渗流特征。

在很多低渗油田中，水相相渗曲线为凹型(含直线型)和凸型(弓背式)[3]。储集层物性越差，伊蒙混层和高岭石含量越高，水敏或速敏越强，水相相渗曲线越容易呈凸型。如红台2301 井岩样43，空气渗透率为1.730 mD，有效渗透率为0.412 mD，孔隙度为8.9%，储集层黏土矿物中伊蒙混层含量为24.8%，高岭石含量为35.2%，测试得到的水相相渗曲线呈弓背式；其他2 块岩样物性差，储集层黏土矿物中伊蒙混层和高岭石含量较低，水相相渗曲线呈现凹型。因此，如果采用(2)式取3 块岩样拟合参数的算术平均值来求取标准油水相渗曲线，容易因低渗岩样占比较大，造成水相相渗曲线偏向凹型。采用(4)式得到的水相指数差异较小，求取的标准油水相渗曲线基本位于3 块岩样油水相渗曲线的中部。

3 新模型的应用

鉴于对Willhite 数学模型作了改进，为便于水驱油规律的研究和矿场应用，按照水驱油解析法[12]，以本文新型油水相渗数学模型为基础，绘制各种经典开发曲线，得出参数关系式。

由(1)式和(4)式，得到无因次采油指数和无因次采液指数[13]：

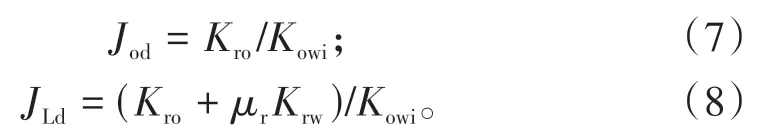
由分流量方程[14]，可得：

利用(7)式—(9)式，可得到红台2301 井无因次采油指数和无因次采液指数曲线(图3)，其变化特征符合中黏度油藏的水驱特征[12]。

图3 红台2301井无因次采油指数和无因次采液指数曲线Fig.3.Curves of dimensionless oil productivity index and dimensionless fluid productivity index for Well HT2301

令a5=μwKowi/(μoKwor)，将(1)式和(4)式代入(9)式，得分流量解析式：

对(10)式求导，得含水率导数[15]：

当出口端含水饱和度等于水驱前缘含水饱和度时，油井含水率等于水驱前缘含水率，代入(11)式，可得：

由Buckley-Leverett 的线性驱替理论可知，水驱前缘含水饱和度和水驱前缘后平均含水饱和度分别满足以下方程[16]：

将(12)式代入(15)式，则：

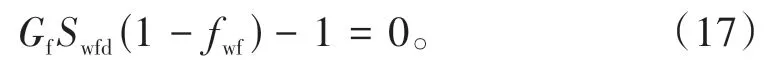
求解(17)式，得到水驱前缘含水饱和度和水驱前缘含水率分别为0.549 0 和0.690 2，再通过(16)式得到水驱前缘后平均含水饱和度为0.606 4(图4)。

图4 红台2301井分流量曲线Fig.4.Curves of distributed flow in Well HT2301

由Welge方程可知[16]，油井见水后，油层平均含水饱和度：

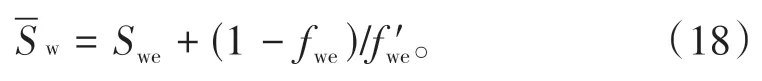
若油层间物性和开采无差异，那么，油井含水率等于出口端含水率，将(11)式代入(18)式，得：

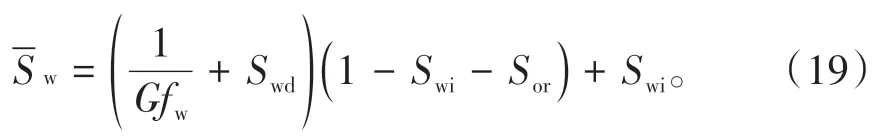
不同含水阶段驱油效率：

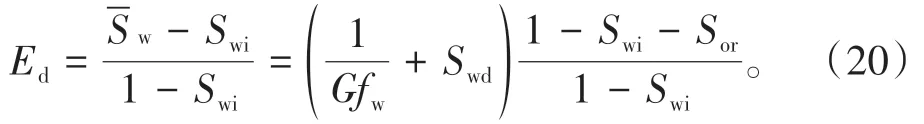
将利用(5)式和(6)式确定的参数值、束缚水饱和度和残余油饱和度代入(20)式，归一化含水饱和度取值范围为0.050～1.000，步长为0.025，可得到一组驱油效率与含水率的变化曲线。由于分流量导数曲线是一个具有极值的双值函数(图5a)，只有计算得到的驱油效率与含水率呈递增关系时才具有实际意义。因此，选用分流量导数曲线右半部分驱油效率和含水率，作为水驱波及体积系数为1 时的采出程度和含水率，再利用广义含水变化规律[17]：

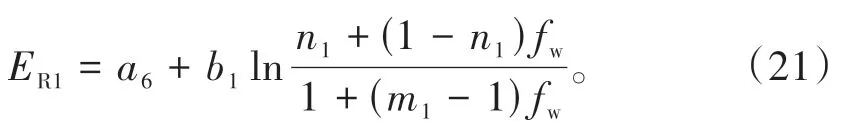
拟合得到水驱波及体积系数为1 时含水变化规律曲线(图5b)。选取红台2301 井水驱波及体积系数为0.56，得到标定的水驱含水变化规律[18]：

图5 红台2301井含水变化规律曲线Fig.5.Variations of water cut in Well HT2301

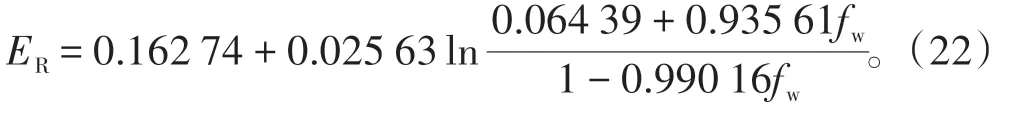
4 结论

(1)新的水相相渗数学模型在拟合不同岩样水相相渗数据时，待定参数估值变化区间小，确定的标准水相相渗曲线受单个岩样拟合参数的影响较小。

(2)部分岩样为弓背式水相相渗曲线时，建议采用本文给出的(4)式进行拟合。

(3)新型油水相渗数学模型减少了复杂的数学推导过程，为矿场应用和水驱规律研究提供了方便快捷的方法。

符号注释

a0、a1、a2、a3、a4、a5、a6、b、b1、c、d、k、m、m1、n、n1、x0、x1、x2、y0、y1——待定参数；

Ed——驱油效率；

ER——采出程度；

ER1——水驱波及体积系数为1时的采出程度；

fw——含水率；

fwe——出口端含水率；

fwf——水驱前缘含水率；

G——出口端含水饱和度函数；

Gf——水驱前缘含水饱和度函数；

JLd——无因次采液指数；

Jod——无因次采油指数；

Kowi——束缚水饱和度下的油相相对渗透率；

Kro——油相相对渗透率；

Krw——水相相对渗透率；

Krwi——本文新模型求取的水相相对渗透率；

Kwor——残余油饱和度下的水相相对渗透率；

Sor——残余油饱和度；

Swd——归一化含水饱和度；

Swe——出口端含水饱和度；

Swf——水驱前缘含水饱和度；

Swfd——归一化水驱前缘含水饱和度；

Swi——束缚水饱和度；

μo——原油黏度，mPa·s；

μr——地下油水黏度比；

μw——地层水黏度，mPa·s。