中国似大地水准面模型CQG2000的梯度分析

聂建亮 张雪萍 郭鑫伟 王莉莉 赵文普

1 陕西测绘地理信息局，西安市友谊东路334号，710054 2 自然资源部大地测量数据处理中心，西安市友谊东路334号，710054 3 自然资源部第二地形测量队，西安市测绘路6号，710054

为满足社会发展需要，我国建立了新一代中国似大地水准面模型CQG2000。21世纪初，陈俊勇等[1-3]和晁定波[4]基于地面重力、卫星测高、船测重力等数据，采用EGM96全球重力场，建立重力似大地水准面模型。利用高程异常控制网对其进行拟合纠正，获取15′×15′分辨率的似大地水准面模型，其中102°E以东地区中误差小于±0.3 m，102°E以西、36°N以北地区中误差小于±0.4 m，102°E以西、36°N以南地区中误差小于±0.6 m。近年来，各省市陆续建立了高精度、高分辨率的区域似大地水准面模型[5-11]。虽然高精度似大地水准面模型能够满足精度要求，但高程转换计算量巨大。以1∶10 000图幅为例，单个图幅的高程基准转换通常需要几十万到上百万个要素点，然而图幅高程基准转换所需的高程精度却较低，在遥感行业，精度一般为dm级甚至m级[12-13]。区域似大地水准面在地球表面空间域内变化较缓，但在地形剧烈变化区域或地类变化过渡区域的变化较为明显。梯度作为数值变化的表征量，可以反映数值在一定区域内变化的大小、方向。CQG2000的梯度用格网点在经、纬度方向上的高程异常空间变化率表示，该数值可以量化不同比例尺图幅内高程异常的变化幅度，可用于分析图幅内平均高程异常对不同比例尺高程精度的适用性。此外，CQG2000的梯度也能反映我国大陆范围内重力场的空间变化特性，有助于解译地球内部质量分布等相关问题。

基于此，本文利用梯度定量描绘CQG2000在全国范围空间域内的变化趋势，分析CQG2000在空间域中的相关性，为建立实用化区域似大地水准面模型提供基础数据，同时也为深入解释似大地水准面变化机理提供科学依据。

1 梯度模型及计算方法

1.1 梯度模型

区域似大地水准面受地球质量分布的影响，在平原、丘陵及高山区的变化趋势不同，变化剧烈区域的结果可能未达到行业应用的精度标准。为更好地表述区域似大地水准面格网模型变化，引入梯度函数，即格网点(B,L)处的梯度：

(1)

式中，f(B,L)为区域似大地水准面模型，B、L为纬度和经度，ΔB、ΔL为纬度、经度方向上的分辨率，m、n为格网模型的行、列数，i、j为梯度矢量的分量方向。

对比分析多种方法发现，三阶反距离平方权差分方法计算效果较好[14]。因此，本文采用坡度的三阶反距离权差分方法计算CQG2000格网点的梯度数值。

1.2 三阶反距离平方权差分方法

采用三阶反距离平方权差分方法选取3×3的移动窗口，计算似大地水准面规则格网点的梯度(图1)，即

(2)

(3)

式中，fB、fL为纬度、经度方向上的梯度分量，ΔB、ΔL为纬度、经度方向上的分辨率，ζ1～ζ9分别为9个格网点的高程异常值。

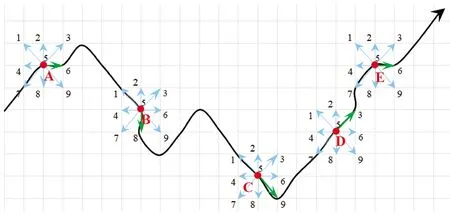
图1 梯度计算示意图Fig.1 Schematic diagram of gradient calculation

梯度方位角α为：

(4)

1.3 梯度精度推导

假设在3×3的窗口内，区域似大地水准面可以表示为曲面ζk=f(Bk,Lk)，且三阶连续可微，按泰勒级数展开并取至三次项，即

f(B+ΔB,L)=f(B,L)+fB(B,L)ΔB+

(5)

f(B-ΔB,L)=f(B,L)-fB(B,L)ΔB+

(6)

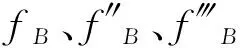
在8个格网点处按泰勒级数展开，整理后的fB为：

(f‴B(ζB,L-ΔL)-f‴B(γB,L-ΔL))+

(f‴B(ζB,L+ΔL)-f‴B(γB,L+ΔL))]}

(7)

令MB、ML为f‴B、f‴L关于B、L的三阶导数最大范围，其误差具有随机性，则有：

(8)

式中，fB一般取式(8)第1项，第2、3项为数据误差及其他误差。

同理可得fL为：

(9)

假设区域似大地水准面格网点中误差为σζ，MB、ML中误差相等且均为M，则σfB为：

(10)

同理可得σfL为：

(11)

由于M数值较小，因此式(10)、(11)中的第2项可以忽略。

根据误差传播定律，由式(4)、(10)、(11)推导出梯度方位角误差σα为：

(12)

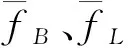
2 CQG2000的梯度分析

为更加精细地描绘CQG2000的空间域变化，在计算梯度时，对原有15′×15′分辨率的模型进行双线性内插处理成5′×5′分辨率的格网模型(忽略内插误差影响)。按照§1.3中公式计算格网点梯度数值及方向，获取全国似大地水准面的梯度，如图2所示。同时，根据表1、2中的全国梯度信息，按照CQG2000精度划分的3个区域范围统计102°E以东(区域1)，102°E以西、36°N以北(区域2)和102°E以西、36 °N以南(区域3)3个区域的梯度分量精度和梯度方位角平均精度，结果见表3、图2。

表1 CQG2000的梯度数值

表2 CQG2000的梯度方位角

表3 CQG2000的梯度精度

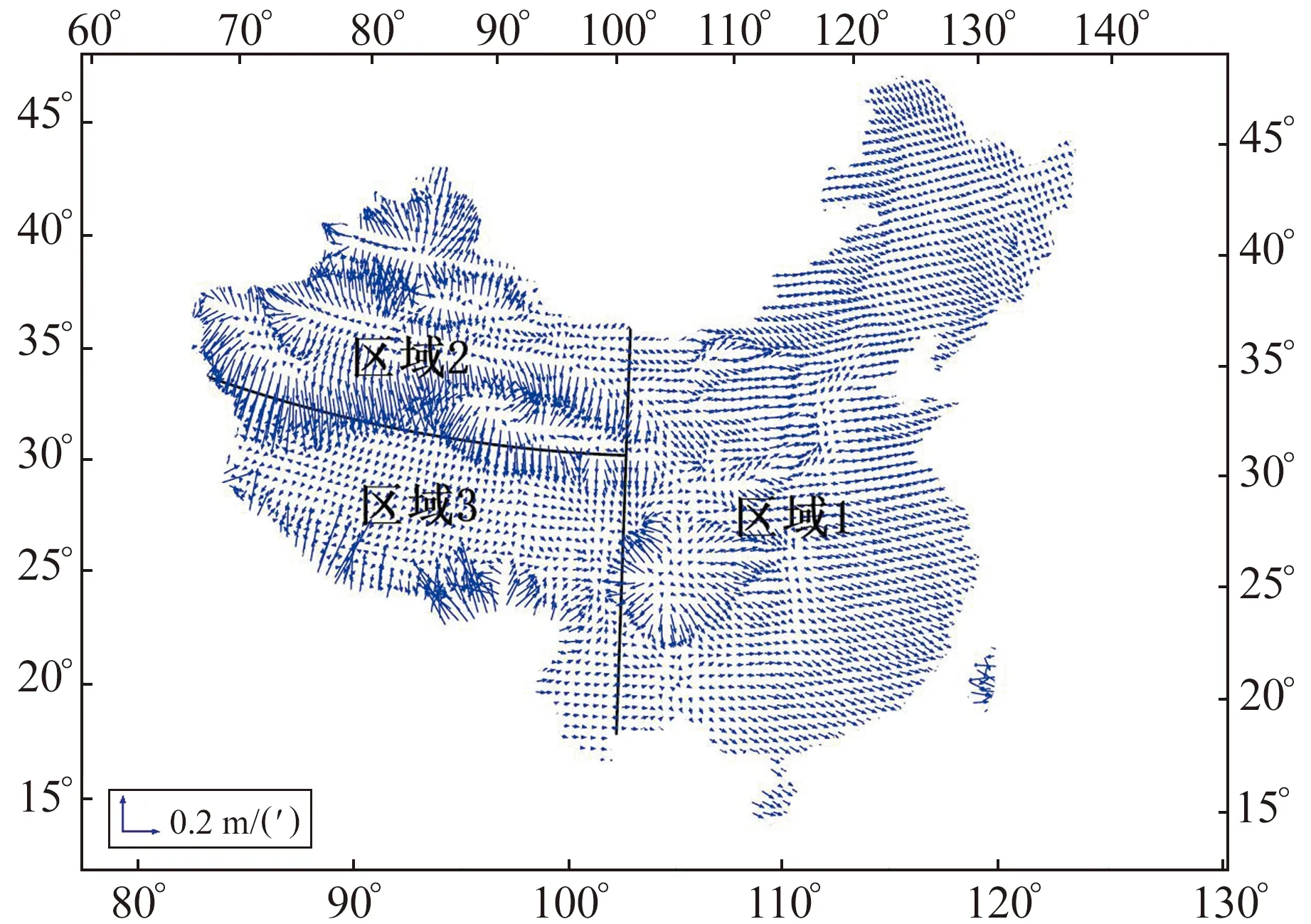
图2 CQG2000的梯度分布Fig.2 The distribution of gradient for CQG2000

综合分析表1～3和图2可知：

1)102°E以东地区CQG2000的梯度方位角方向主要为东，量级小于0.2 m/(′)，且变化平缓。其中，东北地区、华南地区梯度方向主要为东南，角度约为东向南45°；30°～40°N区间内的梯度方位角方向为正东。102°E以西地区CQG2000梯度在不同地类区域的方向不同，且梯度数值变化幅度较大。

2)我国东部、西北、西南地区的梯度分量精度σfB、σfL随似大地水准面格网点精度σζ的增大而增大，随分辨率的增大而减小。西南地区σα误差最大，为50.1°；西北地区σα误差最小，为16.4°。造成上述差异的主要原因为梯度方位角精度σα主要受梯度分量及其精度的影响，较小的梯度数值变化会导致较大的梯度方位角精度变化。进一步说明，相比于梯度分量精度σfB、σfL，梯度方位角误差σα对梯度方位角α更加敏感。

3)新疆北部与南部、青海、成都平原等地存在多个梯度扩散中心，区域似大地水准面格网点高程异常值由中心向四周逐渐增大；喜马拉雅山脉、新疆中部地区出现区域似大地水准面梯度会聚现象；河西走廊也出现区域似大地水准面梯度会聚现象，甘南西部梯度方向为正南，同时顺时针旋转；宁夏南部、甘肃东北部地区区域似大地水准面梯度方向为正东，同时逆时针旋转。喜马拉雅山脉、新疆南部昆仑山脉等地的区域似大地水准面梯度数值较大，最大值位于西藏墨脱县(0.625 m/(′))；青藏高原绝大部分区域的区域似大地水准面梯度较小，变化较平缓。

4)CQG2000梯度变化剧烈区域与我国大山脉走向一致，说明区域似大地水准面与地球内部质量分布密切相关。在喜马拉雅山、昆仑山、天山、秦岭等山脉区域，区域似大地水准面变化速度较大，梯度数值变化为小-大-小。

5)CQG2000自身精度为dm级，实际分辨率为15′×15′。虽然区域似大地水准面梯度精度不高，但能整体反映我国范围内似大地水准面空间域的变化特征。此外，CQG2000梯度与全国范围内的垂线偏差分布[15]一致，仅在西藏东南部地区存在一定差异，可能是该区域缺乏重力等基础资料、似大地水准面精度较低所致。

6)由于CQG2000是利用EGM96参考重力场模型获取高精度重力似大地水准面，再通过GNSS水准点纠正融合得到，因此重力似大地水准面梯度与似大地水准面梯度的总体趋势一致，二者系统偏差较小，梯度大小与方向差异也较小。CQG2000梯度与高精度EGM2008重力场模型梯度在我国中东地区的差异较小，在喜马拉雅山、昆仑山、天山、秦岭等山脉区域存在一定差异，最大差值位于喜马拉雅山地区，约为0.18 m/(′)，可能是CQG2000在该区域缺乏基础资料所致。

3 结 语

梯度信息可反映我国似大地水准面CQG2000在空间域内的整体变化情况，描述不同范围内高程异常变化的量级和方向，可为建立行业所需的实用化模型提供基础数据。整体上看，东北地区CQG2000梯度方位角方向为正东且运动规律与地壳水平运动趋势一致；西部地区梯度方位角方向随地形分布逐渐变化，梯度剧烈变化区域与昆仑山等大山脉走向一致。本文可为进一步开展地球动力学机理研究提供科学依据。此外，高分七号等遥感卫星能够开展大范围1∶10 000立体测图工作，满足各行业对高精度产品的需求，但如何综合利用区域似大地水准面及梯度信息快速、高效地实现卫星遥感影像数据处理的高程自动化转换，是下一步的研究重点。