云贵川地区ZTD垂直剖面格网模型
谢劭峰 张继洪 张亚博 曾 印 唐友兵 熊 思
1 桂林理工大学测绘地理信息学院,桂林市雁山街319号,541006 2 湖北科技学院资源环境科学与工程学院,湖北省咸宁市咸宁大道88号,437100
由于对流层天顶延迟(ZTD)在天顶方向上的误差约为2 m,随高度角的降低误差会增大至20 m[1],因此对流层天顶延迟改正对全球导航卫星系统GNSS实时高精度导航定位及GNSS水汽反演具有重要意义。目前,对流层天顶延迟模型主要分为2大类:1)需要实测气象参数的模型,如Hopfield模型[2]和Saastamoinen模型[3];2)实时模型,如UNB3m模型[4]和EGNOS模型[5]。但上述2类模型均存在一些缺陷:用户位置的实时气象参数难以获取,限制了气象参数模型的应用;UNB3m模型和EGNOS模型的时空分辨率较低,限制了实时模型的应用。GPT2w与GPT3模型是全球格网经验模型,GPT3模型改善了GPT2w模型中的映射函数体系,性能优异且应用广泛,但不能提供对流层天顶延迟的垂直剖面信息。近年来,众多学者利用大气再分析资料对对流层垂直剖面函数展开广泛研究[6],采用二次多项式[7]和负指数函数[8-10]进行模型构建。此外,姚宜斌等[11]利用多源数据建立考虑季节变化的对流层天顶延迟模型;毛健等[12]、黄良珂等[13]建立同时顾及高程和季节变化的对流层天顶延迟模型。上述模型均表现出较好的性能。
在地形起伏极大、气候复杂多变、昼夜大气差异显著的云贵川地区,已有模型难以提供该地区实时高精度对流层天顶延迟信息。基于此,本文利用2015~2017年高时空分辨率的ERA5再分析资料积分计算分层ZTD,分析高程尺度因子的精细时间变化特征,采用负指数函数形式构建顾及高程尺度因子精细时空变化的云贵川地区ZTD垂直剖面格网模型(YZTD-H模型)。其中,YZTD-H1模型顾及了年周期、半年周期、日周期;YZTD-H2模型在YZTD-H1模型的基础上增加了半日周期。本文还利用2018年云贵川地区探空站分层ZTD数据对模型进行精度检验。
1 数据来源
ERA5大气再分析资料(https:∥apps.ecmwf.int/datasets/data/interim-full-daily)是欧洲中尺度天气预报中心ECMWF第五代全球气候再分析数据集,可提供逐小时的地表参数和等压分层数据,有望在未来得到广泛应用。ERA5数据的水平分辨率为0.25°×0.25°,垂直分辨率为37层。探空站数据来源于美国俄怀明大学官网(http:∥weather.uwyo.edu/upperair/sounding.html),该数据可提供从地面到近地空间约30 km的气压、温度、风速、相对湿度等气象参数的分层数据和大气水汽等地表参数,每日进行2次探测(UTC00:00和12:00)。探空站数据为实测值,具有较高的精度和可靠性,可作为模型检验的参考值。本文选取云贵川地区9个探空站对YZTD-H模型进行检验。
2 模型建立
覃泽颖等[14]对ERA5数据计算得到的ZTD精度进行评估,结果表明,ERA5数据可作为ZTD模型建立的数据源。本文利用2015~2017年云贵川地区的ERA5数据,通过积分法计算得到格网垂直剖面ZTD。
2.1 高程尺度因子的特性分析
负指数函数在表示ZTD垂直剖面变化方面具有较好的优越性,公式如下:
(1)
式中,ZTDt为目标高程Ht处的ZTD,ZTDr为起算高程Hr处的ZTD,Hz为ZTD的高程尺度因子。利用2015~2017年云贵川地区ERA5格网垂直剖面ZTD数据对Hz进行拟合,得到每个格网点的逐小时Hz。为分析Hz的精细时间变化特性,选取云贵川地区的2个格网点,计算这2个格网点2015~2017年的日均Hz,对其进行年周期和半年周期的三角函数拟合,并采用快速傅里叶变换法分析其周期性,结果如图1所示。图1(a)、(b)分别为2个格网点3 a日均Hz的时间序列及其拟合线;图1(c)、(d)分别为2个格网点Hz的频谱分析结果。
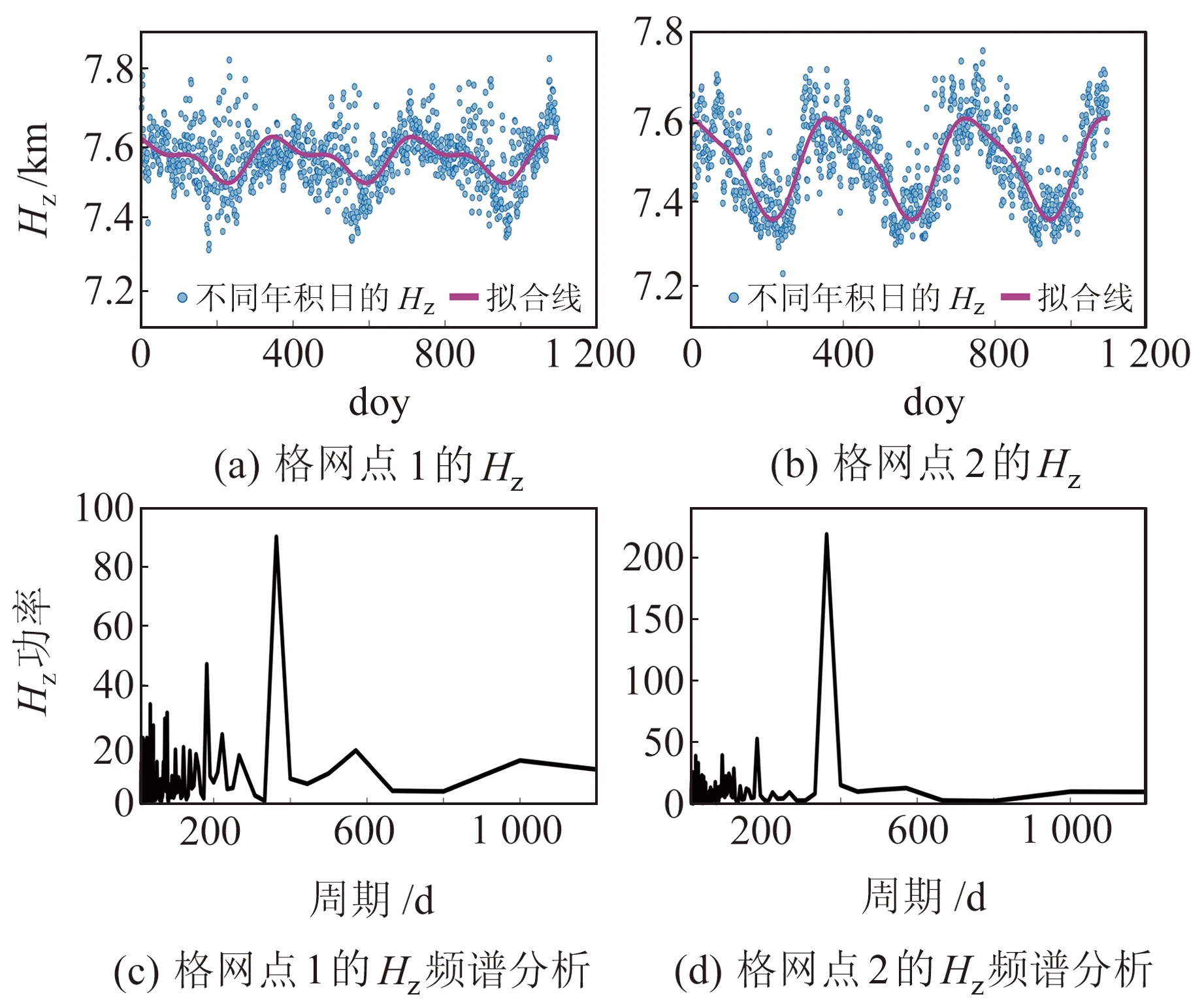
图1 Hz的季节变化及其频谱分析Fig.1 Seasonal variation of Hz and its spectral analysis
由图1可见,Hz存在明显的年周期和半年周期,其中格网点1的半年周期较格网点2更加明显。为分析Hz的精细时间变化特性,同样选取上述2个格网点计算年均UTC 00:00~23:00的逐小时Hz,对其进行日周期和半日周期的三角函数拟合,并采用快速傅里叶变换法分析其周期性(图2)。由图可见,Hz存在显著的日周期和半日周期。

图2 Hz的日变化及其频谱分析Fig.2 Daily variation of Hz and its spectral analysis
2.2 模型建立
在上述Hz周期特性分析的基础上,对Hz进行顾及年均值、年周期、半年周期、日周期、半日周期的三角函数拟合,表达式如下:
(2)

由图3可见,Hz的各拟合系数存在显著的区域性。由于云贵川地区的地势特征为西北高、东南低,因此各拟合系数呈现出由东南向西北逐渐减小的趋势。多个拟合系数在四川盆地和西北高海拔地区存在显著差异,说明拟合系数受海拔影响较大。拟合系数在东南沿海与内陆地区也存在显著差异,可能是沿海与内陆的气候差异和昼夜大气差异所致。由此可知,Hz具有精细的时空分布特征,需要对每个ERA5格网点的Hz进行精细的周期性拟合。考虑拟合系数存储量及半日周期对Hz的影响程度后,本文选用2种方式对2015~2017年云贵川地区ERA5格网Hz进行拟合:顾及年周期、半年周期、日周期的拟合以及顾及年周期、半年周期、日周期、半日周期的拟合。Hz的模型系数以0.25°×0.25°水平分辨率的格网进行存储,最终构建出云贵川地区ZTD垂直剖面格网模型YZTD-H1和YZTD-H2。用户只需提供经纬度、高程、年积日及UTC时等数据,模型便可结合式(1)和式(2)将用户位置从起算高程处的ZTD改正到目标高程处。

图3 Hz各拟合系数的分布Fig.3 Distribution of fitting coefficients of Hz
3 模型精度验证
3.1 模型精度对比
利用云贵川地区9个探空站数据对YZTD-H1和YZTD-H2模型进行精度检验,并将其与性能优异的GPT2w、GPT3模型进行精度对比(GPT2w模型和GPT3模型的水平分辨率均为1°×1°)。UNB3模型可将天顶静力学延迟(zenith hydrostatic delay, ZHD)和天顶湿延迟(zenith wet delay, ZWD)由海平面高度改正至目标高度,但该模型需要气象参数,而GPT2w与GPT3模型可提供全球任意位置的气象参数,因此将二者结合即可实现ZTD的垂直剖面改正。由于作为参考值的探空站数据并非从海平面开始分层,因此需要对UNB3模型进行推导,使其能够对任意高度的ZHD和ZWD进行高程改正。推导结果如式(3)、式(4)所示:
(3)

(4)
式中,ZHDt和ZHDr分别为目标高度和起算高度的ZHD值;ZWDt和ZWDr分别为目标高度和起算高度的ZWD值;Ht和Hr分别为目标高度和起算高度;β为温度梯度;T0为热力学温度;Rd为干气体常量(Rd=287.053 8 J/kg);g为地表重力加速度;λ′=1+λ,λ为水汽梯度。首先采用积分法计算2018年云贵川地区探空站分层ZTD值及首层ZHD/ZWD值,将分层ZTD值作为模型检验的参考值;然后以探空站首层高度作为起算高度,以探空站首层ZTD作为起算值、其他层高作为目标高度,利用YZTD-H1、YZTD-H2模型将探空站首层ZTD依次改正至其他各层。同样,首先以探空站首层高度作为起算高度,以探空站首层ZHD/ZWD作为起算值、其他层高作为目标高度,利用GPT2w、GPT3模型将探空站首层ZHD/ZWD依次改正至其他各层,然后对目标高度的ZHD和ZWD求和,即可得到目标高度的ZTD值。将偏差bias和均方根误差RMSE作为精度指标,计算2018年云贵川地区9个探空站UTC 00:00和12:00的各模型分层ZTD值,得到各模型的总体bias和RMSE,结果如表1所示(单位mm)。
由表1可见,YZTD-H1和YZTD-H2模型均表现出接近于0的平均bias值,分别为-7.81 mm和-7.60 mm,其中YZTD-H2模型略优于YZTD-H1模型;GPT2w和GPT3模型均表现出较大的正bias值,说明二者存在较大的系统偏差,其中GPT3模型略优于GPT2w模型。YZTD-H1和YZTD-H2模型的平均RMSE分别为50.50 mm和50.44 mm,YZTD-H2模型略优于YZTD-H1模型;GPT2w和GPT3模型的平均RMSE分别为79.94 mm和79.93 mm,GPT3模型略优于GPT2w模型。由此可知,YZTD-H1和YZTD-H2模型优于GPT2w和GPT3模型:YZTD-H1模型较GPT2w和GPT3模型的RMSE分别减少29.44 mm和29.43 mm;YZTD-H2模型较GPT2w和GPT3模型的RMSE分别减少29.50 mm和29.49 mm。综上可知,YZTD-H1和YZTD-H2模型具有更高的精度和更好的稳定性。

表1 不同模型的精度统计
3.2 各模型在探空站的精度对比
为分析各模型在探空站的精度表现,计算4种模型在各探空站的年均bias和RMSE,结果如图4所示。
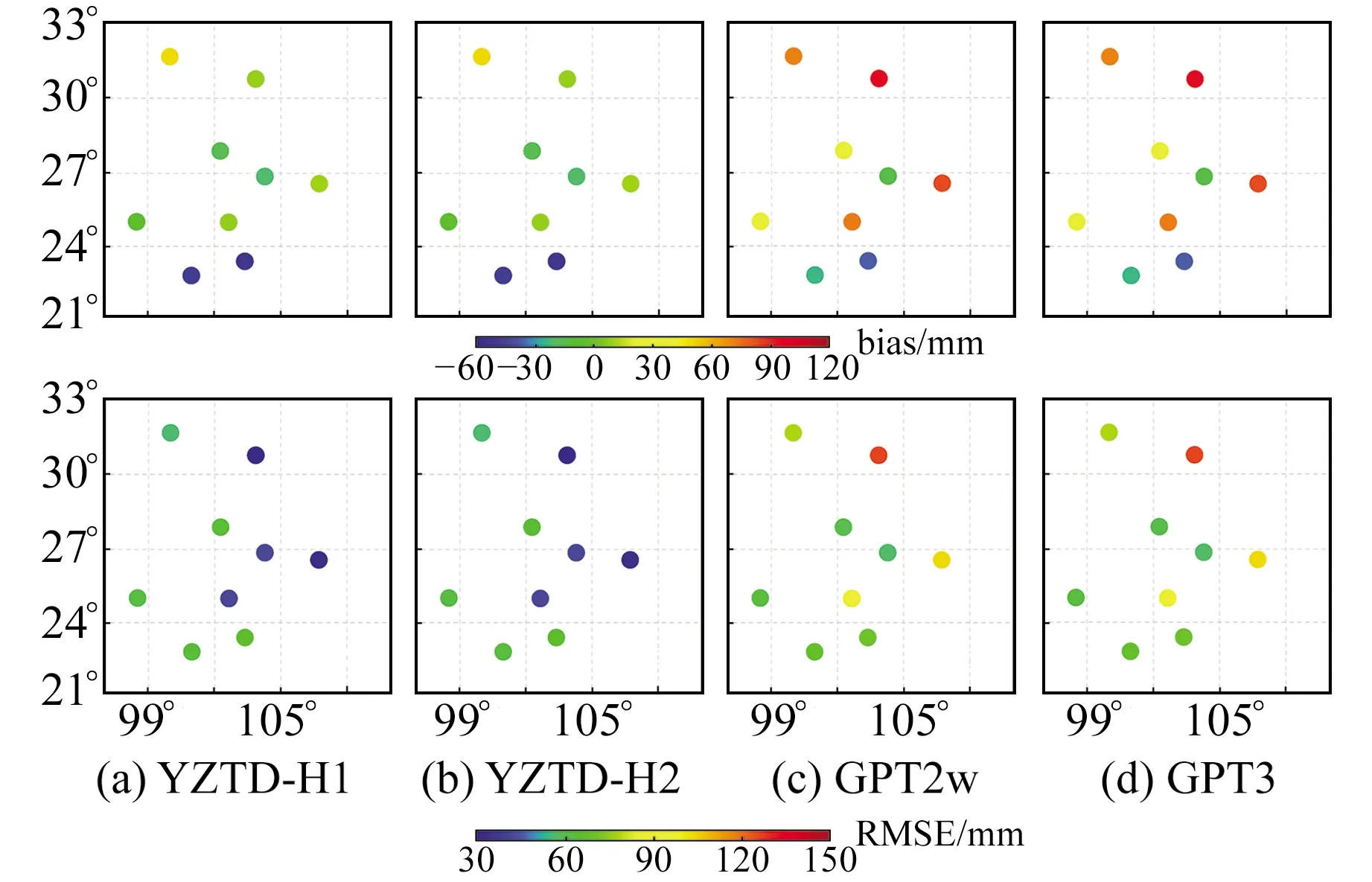
图4 不同模型的精度分布Fig.4 Precision distribution of different models
由图4可见,各模型的年均bias和RMSE存在一定的区域性,可能与云贵川地区复杂的地形、多变的气候和较大的昼夜大气差异有关。YZTD-H1和YZTD-H2模型在各探空站的年均bias总体接近于0,纬度较低的2个探空站表现出较大的负偏差;GPT2w和GPT3模型在各探空站的年均bias总体呈现出较大的正偏差。YZTD-H1和YZTD-H2模型在各探空站的年均RMSE约为50 mm,东北方向的探空站精度更高;GPT2w和GPT3模型在各探空站的年均RMSE均大于60 mm,西南方向的探空站精度更高。由此可知,YZTD-H1和YZTD-H2模型对地理位置的适应性更强。
3.3 模型精度的季节变化特征
由于顾及半日周期的YZTD-H2模型与未顾及半日周期的YZTD-H1模型性能相当,且YZTD-H2模型的RMSE比YZTD-H1模型仅高了0.06 mm,因此选用YZTD-H1模型能够在保证模型精度的前提下减少2个模型系数,减小模型计算量。由于GPT2w模型与GPT3模型精度相当,因此本文仅对YZTD-H1模型与GPT3模型进行精度对比。为分析模型精度的季节变化特征,利用YZTD-H1模型与GPT3模型计算2018年云贵川地区各探空站的日均bias和RMSE,结果如图5所示。

图5 不同模型日均bias和RMSE的散点分布Fig.5 Scatter distribution of daily bias and RMSE for different models
由图5可见,GPT3模型的日均bias呈现出明显的季节性,夏季的正偏差较大;YZTD-H1模型的日均bias均在略小于0的附近波动。GPT3模型的日均RMSE同样呈现出明显的季节性,夏季的RMSE大于春、冬季节,可能是因为夏季特殊的气候导致大气水汽和其他气象参数发生变化,进而导致模型难以精准预测ZTD;YZTD-H1模型的日均RMSE稳定在50 mm附近。由此可知,YZTD-H1模型能够在气候条件复杂和昼夜大气差异大的云贵川地区表现出更好的适应性。
3.4 模型在不同插值高度上的精度变化
为分析模型在不同插值高度上的精度变化,将探空站首层高度与其他层的高度差分为6个区间,统计YZTD-H1模型和GPT3模型在各区间内的bias和RMSE,结果如图6所示。
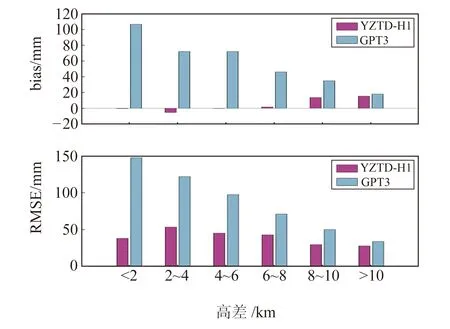
图6 不同模型bias和RMSE随插值高度的变化Fig.6 Variations with interpolated height of bias and RMSE for different models
由图6可见,GPT3模型的bias在各插值高度上均表现出正偏差,且bias随插值高度的增大而减小;YZTD-H1模型的bias在4 km以下为负偏差,在4 km以上为正偏差,整体偏差较小。GPT3模型的RMSE随插值高度的增大而减小;YZTD-H1模型的RMSE随插值高度的增大呈现出先增大后减小的变化趋势,整体变化较为平缓。8 km以上的GPT3模型精度与YZTD-H1模型相当,说明GPT3模型只有在较高的插值高度上才具有较好的适应性,而YZTD-H1在任意插值高度上均有很好的适应性。
3.5 模型在不同误差区间内的分布特征
为分析模型在不同误差区间内的分布特征,将bias和RMSE均分为7个区间,分别统计YZTD-H1模型和GPT3模型的日均bias和RMSE在各区间的数量,结果如图7所示。

图7 不同模型日均bias和RMSE在不同区间内的分布Fig.7 Distribution of daily bias and RMSE for different models in different interval
由图7可见,GPT3模型的bias和RMSE在各区间内均匀分布,说明该模型稳定性较差;YZTD-H1模型的bias集中分布在0 附近,RMSE集中分布在40~60 mm之间,进一步说明YZTD-H1模型具有更优的性能与更好的稳定性。
4 结 语
1)YZTD-H1模型和YZTD-H2模型的总体精度(年均RMSE)均优于GPT2w模型和GPT3模型,YZTD-H2模型精度略优于YZTD-H1模型,二者在各探空站的年均bias和RMSE表现稳定,且并未表现出较为明显的区域性。
2)在YZTD-H1模型与GPT3模型的不同季节精度对比中,GPT3模型表现出明显的季节性,而YZTD-H1模型的全年性能表现稳定。
3)在YZTD-H1模型与GPT3模型的不同插值高度精度对比中,GPT3模型受插值高度的影响较大,而YZTD-H1模型在各插值高度区间内表现稳定,能将RMSE控制在50 mm左右,说明负指数函数形式能够较好地将垂直剖面ZTD模型化。
4)在YZTD-H1模型与GPT3模型的不同误差区间对比中,YZTD-H1模型的日均RMSE集中分布在40~60 mm之间,而GPT3模型在各区间内均匀分布,进一步说明YZTD-H1模型具有更优的性能与更好的稳定性。
综上所述,YZTD-H1模型在不同地理位置、不同季节、不同插值高度上均表现出良好的稳定性和优异的性能,更适用于云贵川地区ZTD的垂直剖面插值计算。本研究对云贵川地区GNSS实时高精度导航定位和GNSS水汽反演具有很好的参考价值。
——环地平弧&环天顶弧

