转台-陀螺飞轮标定系统误差灵敏度分析方法
赵昱宇,李冠璁,崔家山,王雨潇
(1.中国民航大学 电子信息与自动化学院,天津 300300;2.西安电子科技大学 空间科学与技术学院,西安 710126)
1 引言
陀螺飞轮是一种新型姿态控制执行与测量一体化装置,它具有高集成度、低成本的优点,在微小航天器中具有广阔的应用前景[1-2]。作为姿态敏感器,尽管陀螺飞轮与传统机械陀螺仪有相似之处,但为兼顾姿控力矩输出,陀螺飞轮的转子尺寸、质量和转动惯量比传统陀螺仪放大近千倍[3-4]。在系统结构偏差和环境干扰等因素的影响下,相比于传统陀螺仪,作用于陀螺飞轮的干扰力矩也大幅增加,其漂移误差更为显著,误差模型中所包含的误差项也更为复杂[5]。
为使陀螺飞轮实现较高精度的姿态测量,通常利用转台进行多位置标定试验,以实现漂移误差的标定与补偿[6]。受伺服控制精度、加工制造与装配工艺水平等的限制,标定系统不可避免受到多种误差因素的影响[7]。相比于传统陀螺仪,标定系统的多种误差因素会给陀螺飞轮的标定精度带来更为显著、不容忽视的影响。因此,有必要研究多种误差因素对转台-陀螺飞轮标定系统的影响,通过误差建模与误差灵敏度分析,为陀螺飞轮标定精度的提升提供有效指导。
在转台误差对传统惯性仪器标定精度的影响分析方面已有较多研究成果,文献[8-9]分别分析了典型转台误差因素对MEMS陀螺和激光陀螺标定精度的影响;文献[10-11]主要探讨了转台不正交度、定位精度等因素对惯性测量单元标定精度的影响;文献[12]则针对液浮陀螺仪提出了一种降低转台误差影响的标定策略。上述研究成果为标定试验设计、标定精度提升提供了理论支撑,但它们多局限于单个误差因素或部分误差因素的讨论,缺少对误差因素的全面分析和对多误差因素共同作用下误差传递机理和误差灵敏度的讨论。此外,现有文献多在已知待标定参数量级的前提下给出定量分析结果,相关方法和结论往往推广性较差。而陀螺飞轮作为一种新型惯性仪器,为保证其标定精度,文献[6,13]从多元回归数据处理的角度分别对标定方案和标定参数解算进行了研究,其他相关研究成果较少。
因此,本文综合考虑转台自身的定位误差、轴线回转误差、垂直度误差、相交度误差、以及转台与陀螺飞轮间的安装误差等因素的影响,研究多误差因素作用下的误差传递机理。针对标定系统误差因素较多、误差传递模型非线性、误差变化范围较大的问题,给出全局误差灵敏度分析方法,以实现关键误差因素的辨识,为标定系统误差指标的确定、标定试验的优化设计等提供理论支撑。
2 陀螺飞轮标定原理
陀螺飞轮是一种适用于微小航天器的新型姿态测控一体化装置,其结构如图1所示[2]。结构非理想因素、外部环境等会导致干扰力矩作用于陀螺飞轮转子,从而引起漂移误差。为实现较高精度的姿态测量,需要进行多位置试验对其漂移误差进行标定,以实现漂移误差的补偿,含有补偿项的测量方程可简化描述为[5]
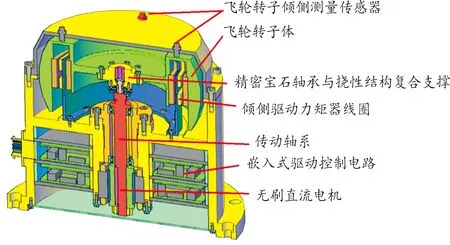
图1 陀螺飞轮结构示意图
(1)
式(1)中: ωbx,ωby为外部输入角速度;Tcx,Tcy为两轴控制力矩;方程中其余项表示漂移误差,其ax,ay,az分别为沿陀螺飞轮三轴的加速度分量,dx(·),dy(·)分别代表陀螺飞轮两敏感轴的漂移误差系数,其下标表示该误差项与加速度的相关性。
在地面测试环境中可以利用两轴转台提供精确的位置基准,陀螺飞轮作为转台负载,通过夹具固装于转台内环,转台与陀螺飞轮的初始安装示意图由图2给出。
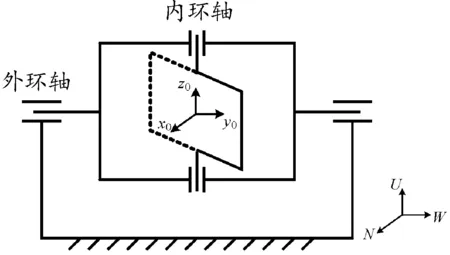
图2 转台与陀螺飞轮安装示意图
通过将转台按照标定路径转动到多个位置,可以使陀螺飞轮在不同位置敏感不同的重力加速度和地球自转角速度分量,从而根据测量方程建立如式(2)所示的多元回归模型,合理设计标定位置可使式(2)满足有解条件,则可通过解算式(2)实现对漂移误差系数的标定:
yg=Agβg+eg
(2)
式(2)所示的多元回归模型中,βg为待标定的误差参数向量,eg为观测误差向量,而系数矩阵Ag和观测向量yg中的各元素则由重力加速度和地球自转角速度在各标定位置的投影分量决定。
可见,重力加速度分量和地球自转角速度分量是陀螺飞轮的标定基准量,它们在不同标定位置的取值取决于转台通过内外环旋转而提供的不同姿态。实际系统受多种误差因素的影响,在标定试验中,陀螺飞轮三轴的实际指向必然与理想值间存在偏差,使得标定基准量存在误差,从而影响陀螺飞轮的标定精度。因此,为有针对性地提升标定精度,第2节考虑标定系统的多种误差来源,建立误差传递模型,以获得多误差因素与标定基准量误差之间的映射关系。
3 标定系统误差建模
3.1 标定系统误差来源
转台-陀螺飞轮标定系统的误差来源包括:转台定位误差、转台轴系回转误差、转台垂直度误差、转台相交度误差以及陀螺飞轮安装误差。为便于后续进行误差描述和建模,将上述误差因素总结如表1所示。

表1 标定系统的误差因素
3.2 基于多体系统理论的误差模型推导
将转台-陀螺飞轮标定系统视为多刚体系统,基于多体系统理论对其误差模型进行推导。
为便于误差描述和建模,定义如下坐标系:基座坐标系F0:O0X0Y0Z0,外环坐标系F1:O1X1Y1Z1,内环参考坐标系F2:O2X2Y2Z2,内环坐标系F3:O3X3Y3Z3,以及负载坐标系F4:O4X4Y4Z4。坐标系F0,F1,F3,F4分别与转台基座、转台外环、转台内环、陀螺飞轮固连,F1的x轴与转台外环轴线方向一致,F3的z轴与转台内环轴线方向一致。坐标系F2与F1间的变换体现转台内外环轴间的垂直度和相交度误差。设转台外环轴和内环轴的期望转角分别为φ1和φ2,标定系统的误差因素如表1所述,则相邻坐标系间的相对运动关系如图3所示。
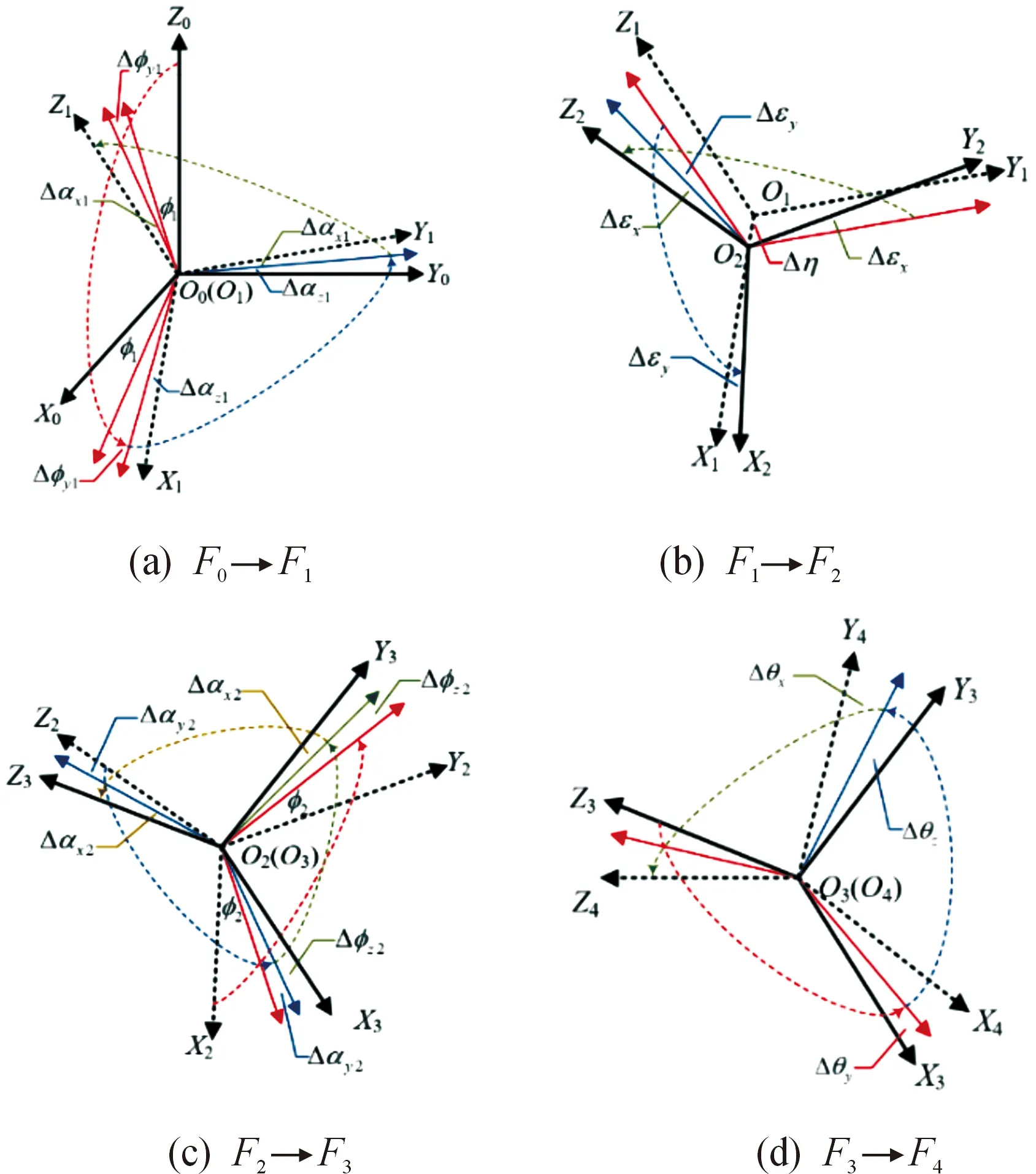
图3 相邻坐标系之间的运动关系
根据多体运动学理论,相邻两坐标系Fi→Fi+1的相对位姿变换关系可用齐次变换矩阵表示,记作iTi+1。则基座坐标系与外环坐标系间的变换关系为
(3)
外环坐标系与内环参考坐标系间的变换关系为
(4)
内环参考坐标系与内环坐标系间的变换关系为
(5)
内环坐标系与负载坐标系间的变换关系为
(6)
定义Td,Tt分别为理想情况下和多误差因素作用下陀螺飞轮相对于惯性坐标系的位姿变换矩阵,则
(7)
(8)
考虑多位置标定试验中,转台负载端的姿态误差会影响陀螺飞轮三轴敏感的地球自转角速度和重力加速度分量,因此,定义Rd,Rt分别表示理想情况和多误差源作用下陀螺飞轮相对于惯性坐标系的姿态变换矩阵,则有
Rd(φ)=M·Td·MT
(9)
Rt(φ,χ)=M·Tt·MT
(10)
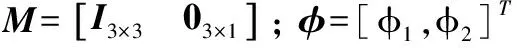
χ=[Δφy1,Δφz2,Δαx1,Δαz1,Δαx2,Δαy2,
Δεx,Δεy,Δθx,Δθy,Δθz]T
注:χ中不包含转台相交度误差Δη,这是由于Δη只影响转台负载端的位置而不影响姿态,因此可不考虑其对标定精度的影响。
在多位置标定试验中,假设理想情况下陀螺飞轮的初始指向为北-西-天。记ωe为地球自转角速度,λ为试验地点纬度。在理想情况下,投影在陀螺飞轮各轴的重力加速度分量和地球自转角速度分量只与转台转角φ相关,即
[axayaz]=[0 0 -g]·Rd(φ)
(11)
[ωexωey] =[ωecosλ 0 ωesinλ]·Rdφ)·Mω
(12)
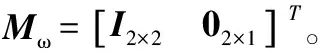
而当标定系统受多种误差因素影响时,重力加速度和地球自转角速度分量不但与转台转角φ相关,还与误差参数χ相关,即
(14)
根据式(11)~式(14),转台-陀螺飞轮标定系统中的多种误差因素共同引起的标定基准量误差为
[ΔaxΔayΔaz] =[0 0 -g]·ΔR(φ,χ})
(15)
[ΔωexΔωey]=[ωecosλ 0 ωesinλ]·ΔR(φ,χ})·Mω
(16)
式中:ΔR(φ,χ})=Rt(φ,χ})-Rd(φ)表示转台负载端的姿态误差矩阵。
将式(3)~式(10)代入式(15)~式(16)中,可计算多种因素共同作用所引起的标定基准量误差,式(15)~式(16)为转台-陀螺飞轮标定系统的误差传递模型。该误差传递模型综合考虑了标定系统的多种误差因素,且以标定基准量误差作为终端输出误差有效避免了模型中包含待标定参数,这一模型具有更好的适用性与推广性。
4 标定系统误差灵敏度分析方法
为充分探讨各误差因素对基准量误差的影响程度,本节基于误差传递模型进行误差灵敏度分析。分析结果能够为关键误差因素的辨别、标定系统误差指标的确定、标定试验的优化设计等提供理论依据,对降低标定试验成本、提升陀螺飞轮的标定精度具有重要意义。
常规误差灵敏度分析一般采用局部分析方法,即基于微分或差分理论,在固定其余因素的前提下,只改变被研究单个因素的数值,可以得到该因素的灵敏度分析结果[14-15],这类方法较为简单、易于计算。然而,考虑转台-陀螺飞轮标定系统的标定精度受诸多因素影响,需要在变化范围内同时对多个误差因素进行灵敏度分析,且其误差传递模型具有非线性,局部灵敏度分析方法无法给出可靠的分析结果。因此,本文采用一种全局灵敏度分析方法——Sobol法[16-18]以充分探讨各个误差参数对标定基准量误差的影响程度。
4.1 全局灵敏度
假设待分析模型为Y≡f(X),X∈Rk为k维输入向量,X=[X1,…,Xk]。根据Sobol方法,对于平方可积的f(X),可将其分解为[16]
(17)
式(17)中各加数项之间相互正交,从而能够对总方差进行分解,得到
(18)
式(18)中总方差V表示所有因素对模型输出的影响,Vi表示单个因素Xi对输出的影响,Vij表示Xi和Xj两因素交互作用对输出的影响,以此类推。输入参数对输出的灵敏度可用其对输出总方差的贡献量来评价,其中最为常用的灵敏度系数为一阶灵敏度和总体灵敏度,它们分别定义为
(19)
(20)
其中:~i表示除Xi外的其他所有因素,Si代表因素Xi单独作用对总方差的贡献,未包含Xi与其他因素相关的更高阶方差;STi则表示所有来自因素Xi的方差的总贡献。
4.2 基于Sobol法的标定系统误差灵敏度分析
根据Sobol方法,所定义的灵敏度系数可通过蒙特卡洛方法进行数值计算,在此基础上,给出转台-陀螺飞轮标定系统的误差灵敏度分析算法如下:
算法步骤:
1) 确定采样样本数N,误差因素个数k,转台内外环转角φ,待分析模型f(χ)∈{Δax,Δay,Δaz,Δωex,Δωey};
2) 在误差参数空间Θχ内进行蒙特卡洛随机采样,生成N×k维采样矩阵A和重采样矩阵B;
3) 初始化i=1;
5) 根据下式计算第i个误差因素的灵敏度系数:
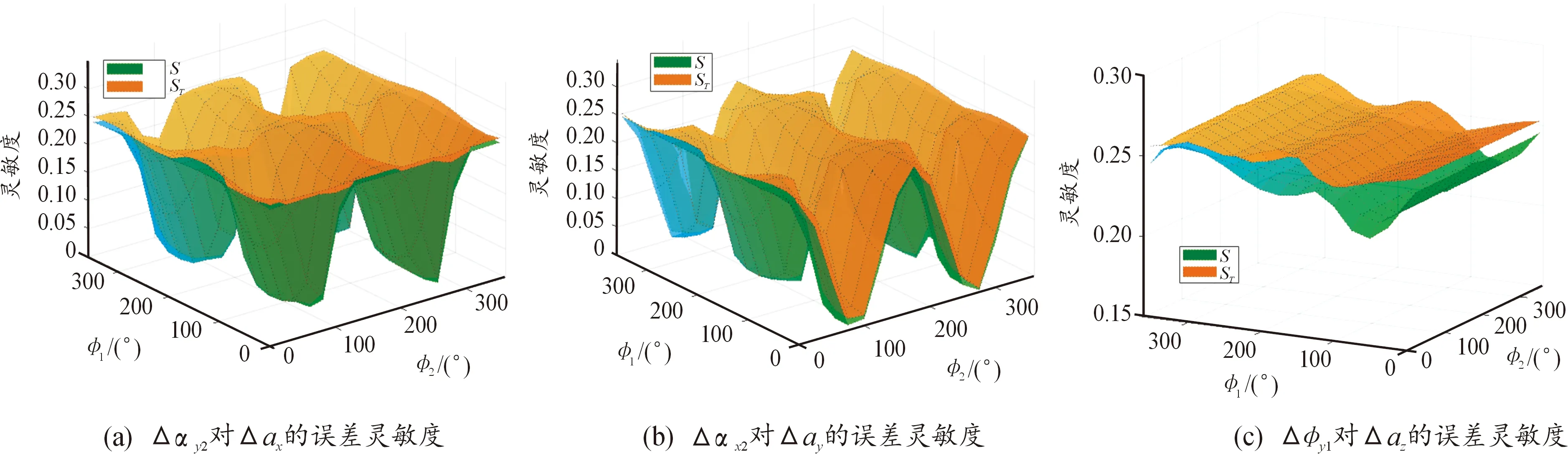
6) 若i 根据给出的分析算法,设定采样样本数N=1 000,对式(15)~式(16)所描述的标定系统误差传递模型进行灵敏度分析。考虑工程实际,本文在如下误差参数空间内: Θχ={χ∈R11∶∀χi∈[-2′,2′]} 分析11个误差因素对5个标定基准量的影响。 如误差传递模型所示,标定基准量误差随转台转角φ1、φ2变化而变化,在每一转角位置应用上述算法可得到一组误差灵敏度分析结果。为从整体上讨论各个误差因素的影响程度,将不同转角位置的误差灵敏度取平均值,分析结果如图4所示。 根据图4所示的误差灵敏度分析结果,对于x轴标定基准量ax和ωex,误差因素Δαx2,Δθx的灵敏度为10-5量级,其影响可以忽略;而误差因素Δαy2,Δθy的灵敏度为其余误差因素的3~5倍,其影响最大。反之,对于y轴标定基准量ay和ωey,Δαy2,Δθy的灵敏度为10-5量级,其影响可以忽略;而Δαx2,Δθx的灵敏度为其余误差因素的3~5倍,其影响最大。Δφz2,Δαx1,Δαz1,Δεx,Δθz对z轴标定基准量az的灵敏度为10-4~10-5量级,其影响可以忽略;而Δφy1,Δεy的灵敏度为其余误差因素的4~5倍,其影响最大。综合上述分析,Δαx2,Δαy2,Δφy1,Δεy,Δθx,Δθy是标定系统的关键误差来源,因此,为兼顾陀螺飞轮的标定精度和试验成本,可以有针对性地对上述关键误差因素的误差指标提出更高要求。 注:根据误差传递模型(15)~(16),χ对同一轴标定基准量的误差传递关系相同,因而各误差因素对同一轴标定基准量的误差灵敏度分析结果一致。 如图4所示,同一误差因素的一阶灵敏度和总体灵敏度值相差不大,两者之差不超过10-3量级,这表明各误差因素间的交互作用相对较小。 图4 误差灵敏度均值 另外,考虑误差灵敏度随转台转角位置的变化而变化,对于上述关键误差因素,有必要进一步探讨其误差灵敏度在转角空间的分布。根据灵敏度计算结果,Δαy2,Δθy对x轴标定基准量的影响几乎一致,Δαy2,Δθy对y轴标定基准量的影响几乎一致,而Δφy1,Δεy对z轴标定基准量的影响也几乎一致,因此图5以Δαy2对Δax、Δαx2对Δay、Δφy1对Δaz为例,给出不同转台转角下的误差灵敏度分布结果。 如图5(a)和图5(b)所示,对x轴和y轴标定基准量来说,误差灵敏度随两轴转角变化呈现周期性变化,因此,在标定试验设计环节,根据灵敏度分析结果可以合理设计标定位置,以尽量减小误差因素的影响,这为标定试验的优化设计提供了理论依据。现有研究通常将标定试验设计问题转化为多目标优化问题进行求解[6],因此可将误差灵敏度数值作为优化问题的约束条件之一,以进一步改善标定试验精度。从图5(c)可见,Δφy1(及Δεy)在整个转角空间均对z轴标定基准量产生明显影响,因而很难通过试验设计减小其影响,为保证标定精度可有针对性地对Δφy1,Δεy的误差指标提出更高要求。 图5 不同转台转角下的误差灵敏度 建立了转台-陀螺飞轮标定系统的误差传递模型,误差传递模型考虑了多种误差因素的共同作用,且为显式映射形式便于进行定量分析。提出了基于Sobol法的标定系统全局误差灵敏度分析方法,根据分析结果确定了标定系统的关键性误差因素,实现了误差溯源。 定量分析结果为进一步提升陀螺飞轮标定精度提供了理论依据,一是合理设计标定试验位置能够减小关键误差因素Δαx2,Δαy2,Δθx,Δθy的影响,二是严格控制误差指标要求能够减小关键误差Δφy1,Δεy的影响。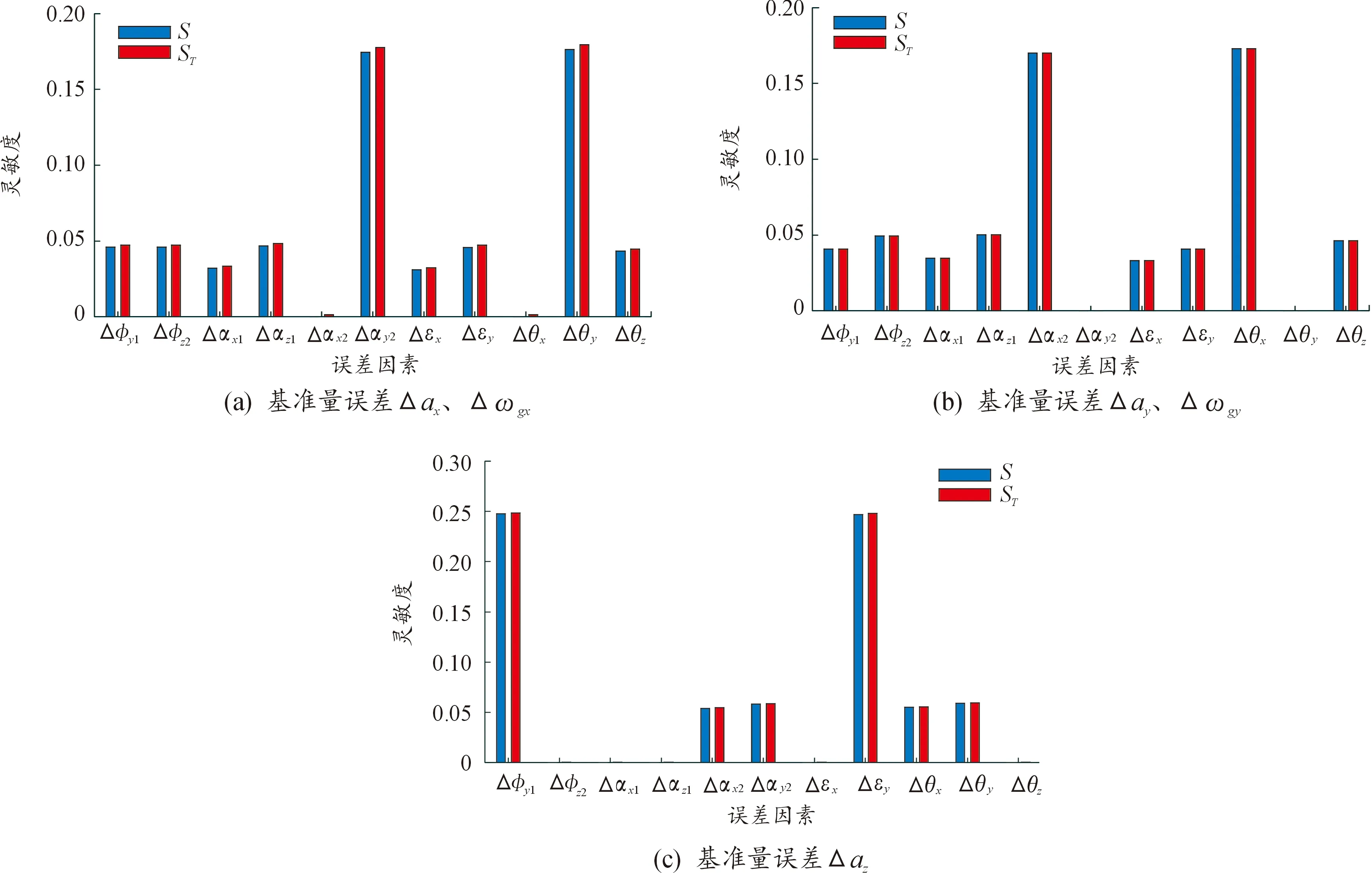
5 结论

