Meat Grinder放电特性分析

向红军,曹根荣,吕庆敖,雷 彬,梁春燕

(1.陆军工程大学石家庄校区 弹药工程系，石家庄 050003；2北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

1 引言

电磁轨道炮是一种依靠电能加速宏观弹丸到超高速的新概念动能武器，具有初速高、射程远、噪声小、防御难等优点，可应用于超远程火力支援、防空反导等方面，成为各军事大国的研究热点。制约电磁轨道炮发展的一个重要原因在于其脉冲功率电源的小型化和机动性[1-3]。作为一种具有强耦合电感储能的脉冲功率电源，Meat Grinder[4-5]储能密度非常高，能够通过电磁耦合的原理实现电流放大功能，从而满足电磁轨道炮所需脉冲大电流的要求，具有广阔的应用前景[6-9]。

目前关于Meat Grinder的研究已经有很多[10]，主要集中在基于超导储能电感的Meat Grinder[11-12]，将漏感能量再利用的STREYCH Meat Grinder[13-14]，能够克服大电流关断困难的基于ICCOS换流的Meat Grinder[15-17]以及兼顾漏感能量利用以及大电流关断功能的Meat Grinder with SECT[18-20]等方面。然而，对于Meat Grinder基础结构的研究较少，导致在进行电路设计时，通常首先利用软件进行建模，仿真计算，而后观察系统性能。上述方法存在耗时较长，效率不高，程序可移植性差等问题，因此，仿真计算方法不便对电路进行系统优化。

基于电路系统模型的数学解析计算方法，计算速度快且精度高，且可灵活修改参数，方便系统优化设计。为此，本研究着重于对Meat Grinder输出性能进行理论分析,从而为实验提供参考。

2 基于电路模型的Meat Grinder工作过程

图1展示的是Meat Grinder的基本结构[4]。其中，Us为直流充电电源；R为充电回路的电阻；L1～Ln为紧密耦合的理想电感；电感值均为L；且每2个电感之间的耦合系数均为k；D为晶闸管；R0和L0为负载电阻和负载电感；在这里假设所有的开关均为理想开关。

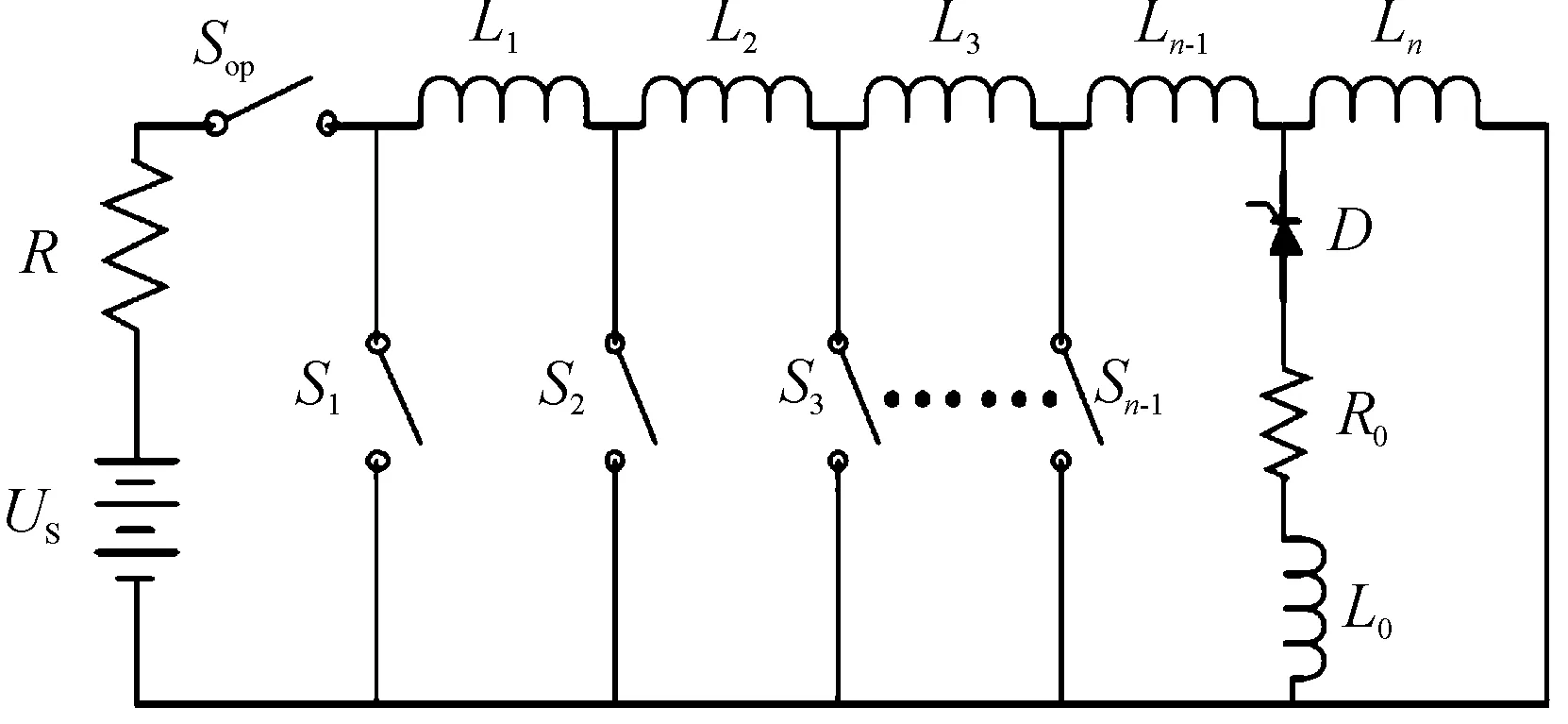
图1 Meat Grinder基础结构

在初始状态时，开关S1～Sn-1断开，开关Sop闭合，晶闸管未触发，直流电源Us对储能电感链进行串联充电，此时电路为一阶RL电路，充电至初始电流I0后，S1闭合，同时Sop断开。

为了达到电流放大的目的，从i=1开始，闭合Si+1的同时断开Si。由于放电回路被断开，Li中的电流会迅速下降，突变为零。而电感之间存在强耦合，根据法拉第电磁感应定律，Li中磁通减小，在剩余电感中会产生感应电动势，导致电流增大，补偿由于Li中电流下降带来的磁通损失，上一级被断开电感Li中所储存电磁能就被转移到了剩余电感中，通过不断地重复此操作，从而实现能量传递，最终触发晶闸管D，同时断开Sn-1，Ln中的电流将以初始电流的数倍，对负载进行放电。相比于直流电源直接对负载进行放电，Meat Grinder极大地提升了放电电流和放电功率。

3 Meat Grinder模型的计算

3.1 单级耦合

首先对单级耦合时的Meat Grinder工作过程进行分析。文献[10]认为在开关闭合前后，储能电感链中的磁通量守恒，可以利用此方法大致估计出耦合后的电流。这种方法虽然具有一定理论依据，但无法对电流的变化做出准确计算。实际上，电流变化的基本原理是电磁感应原理，单独进行一次开关断开动作，其物理模型可以看作是一个变压器模型，断开的开关可看作一个无穷大的电阻Ropen，基于此设想，构建了如图2所示的等效电路模型。

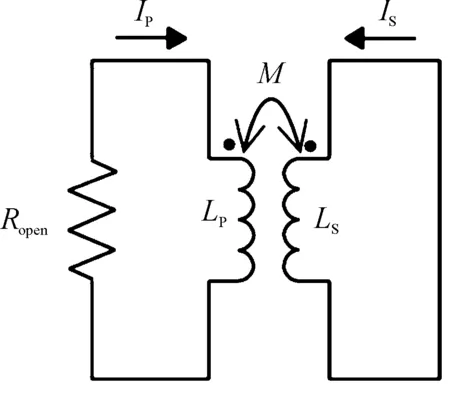
图2 单级耦合电路的等效电路图

在图2中，Lp为初级线圈电感，Ls为次级线圈电感，Ip为流经初级线圈的电流，Is为流经次级线圈的电流，初级线圈和次级线圈之间的互感为M。在这里将Ip降低到零的瞬态过程宏观化，以便利用数学方法进行计算，由电路的初始状态可知Ip(0)=Is(0)=I0。根据基尔霍夫电压定律，可列出下列方程组：

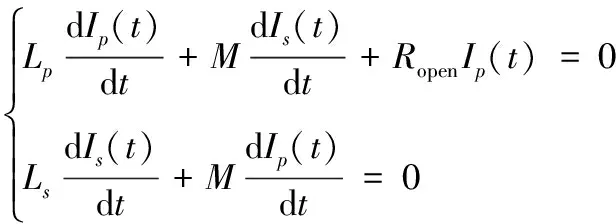
(1)

通过对此方程进行拉氏变换求解，可以得到Ip、Is关于时间t的表达式：

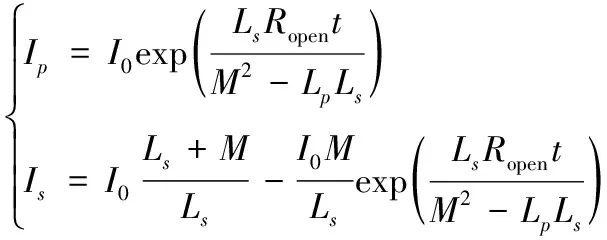
(2)

分析Ip和Is，可以发现当t=0时，Ip=I0，Is=I0，因此电路的初始条件是满足的。下面考虑当t+∞时，Ip和Is的取值。

由于M2-LpLs≤0，且Ropen～+∞，因此当t变化很小时，指数项即变为0，I1和I2最终的电流为

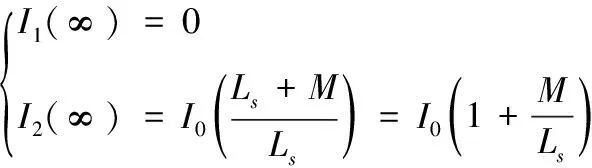
(3)

从式(2)和式(3)可以看出，从开关断开到Ip和Is电流稳定，Ip电流随着时间呈指数律衰减，并且Ropen越大衰减越快，互感越大衰减越快。最终衰减到无限趋近于零；Is电流随着时间指数上升，最终趋近于I0(1+M/Ls)。因此可得到单级耦合时电流放大倍数ε的表达式：

(4)

由式(3)，可得到单级耦合时的能量利用率η以及能量损耗ΔE的表达式：

(5)

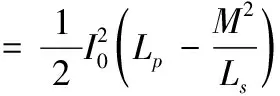
(6)

3.2 多级耦合

以上为单级耦合Meat Grinder输出性能变化情况。而多级耦合是单级耦合的叠加，因此其输出性能可以通过对单级耦合的对应参数进行叠加得到。

由给定条件，假设多级耦合Meat grinder中每两级电感之间的耦合系数均为k，可得到Lp，Ls，M在n级电路中的表达式：

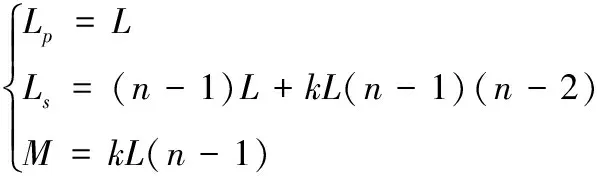
(7)

在具有n级电感的Meat Grinder中，对式(4)(5)(6)进行叠加，可以得到电流放大倍数εsum，能量损耗ΔEsum，能量利用率ηsum的表达式：

(8)

(9)

(10)

利用Matlab进行数值计算，得到电流放大倍数εsum，能量利用率ηsum，能量损耗ΔEsum，关于级数n和耦合系数k的变化曲线，如图3、图4、图5所示。

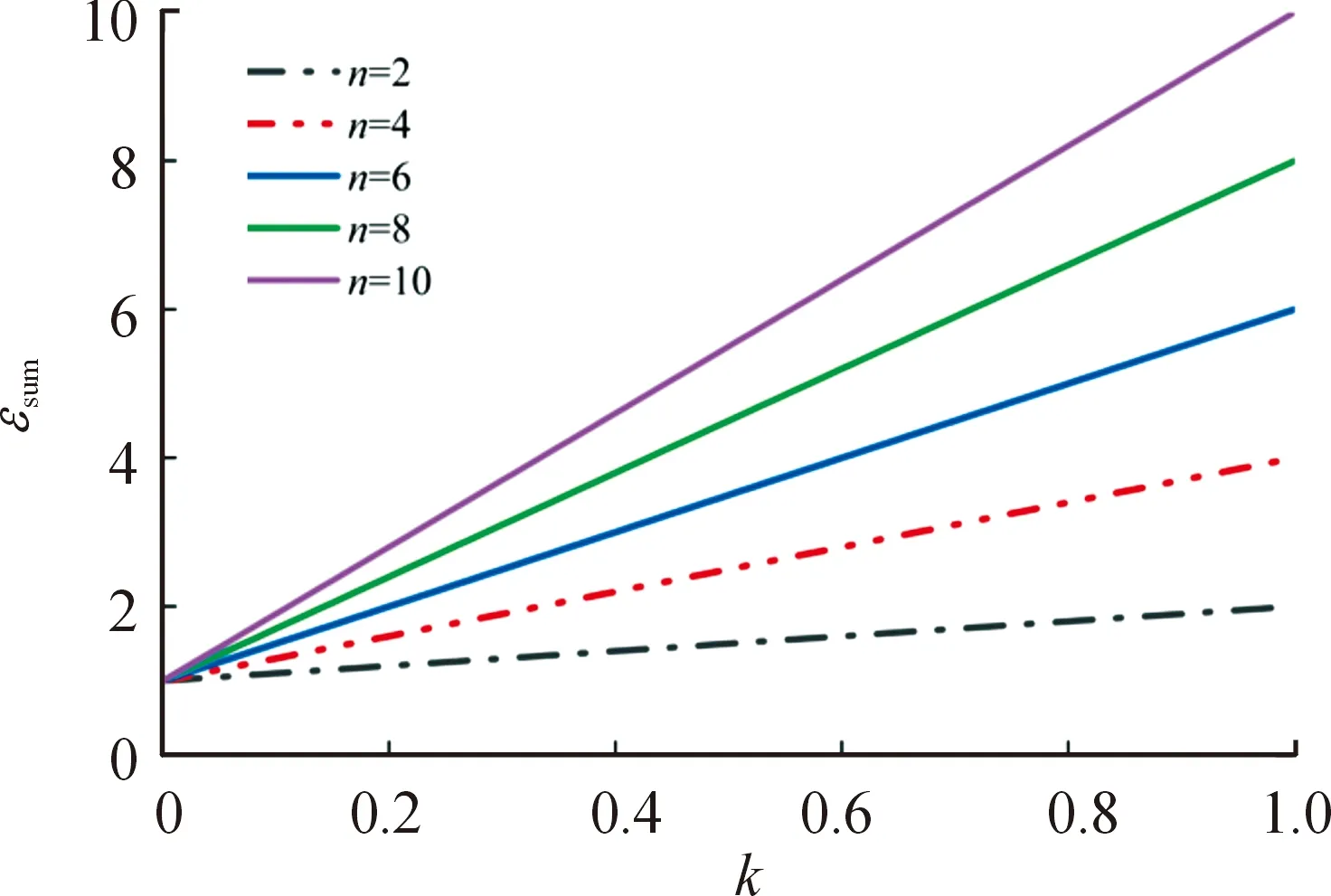
图3 电流放大倍数εsum随耦合系数k与级数n的变化

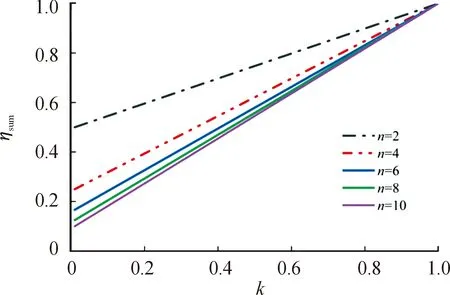
图4 能量利用率ηsum随耦合系数k与级数n的变化

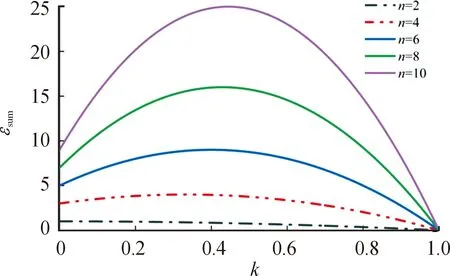
图5 能量损耗ΔEsum随耦合系数k与级数n的变化

在图3、图4、图5中，对于确定的耦合系数k，提升n能够显著提高电流放大倍数εsum，但能量损耗ΔEsum也会增大，能量利用率ηsum则相应降低；对于确定的级数n，当提高耦合系数k时，电流放大倍数εsum和能量利用率ηsum都呈线性增长，能量损耗ΔEsum却呈二次曲线的形式。

从物理意义上考虑，当提高级数n时，MeatGrinder初始储能增大，同时断开开关的次数也会增多，能量损耗ΔEsum变大，但增加一级电感带来的损耗要小于其增加的初始储能，因此最终输出的电流仍会增大；能量利用率ηsum随着n的减小而提高，但以此种方式提高能量利用率ηsum的原理并不是减小能量损耗，而是当n降低时，每一级电感的能量占初始储能的比值提高，即便耦合系数k为零，能量利用率仍然能够维持在较大值。

当提高耦合系数k时，MeatGrinder系统互感增大，因此初始储能增大，并且断开每一级时的能量损耗减小，因此电流放大倍数εsum和能量利用率ηsum也会增大。能量损耗ΔEsum与耦合系数k的关系呈二次曲线的形式，这是因为当耦合系数k较低时，虽然能量利用率ηsum不高，但系统初始储能也较少，因此耗损能量不多；但随着耦合系数k的增大，能量利用率ηsum提高，系统初始储能也增大，此时系统损耗的能量相比于低耦合系数时也要更多；随着k进一步增大，能量利用率ηsum达到较高水平，损失的能量仅占系统能量总量极小的一部分，因此能量损耗会降低，能量损耗随着k的变化呈现出二次曲线的形式。

对式(8)(9)(10)进行进一步推导，可得

εsum=(n-1)×k+1

(11)

(12)

(13)

式(11)(12)(13)即多级Meat Grinder输出电流放大倍数εsum，能量损耗ΔEsum，能量利用率ηsum的表达式，从中同样可以看出能量损耗ΔEsum与耦合系数k的关系呈二次曲线。

3.3 仿真分析

利用simplorer仿真软件对5级Meat Grinder进行输出性能进行仿真验证，由于能量利用率ηsum以及能量损耗ΔEsum可以通过电流的初态和终态求解，因此仿真主要对电流的变化进行分析。

Meat Grinder电路主要用于提供强电流，而电流在电路中长时间的流动会导致衰减，因此理论上各个开关的触发间隔越短，就越能够减小电能的消耗，同时考虑到开关动作的实际误差，开关的触发间隔设置为0.1 ms，仿真电路参数设置如表1所示。

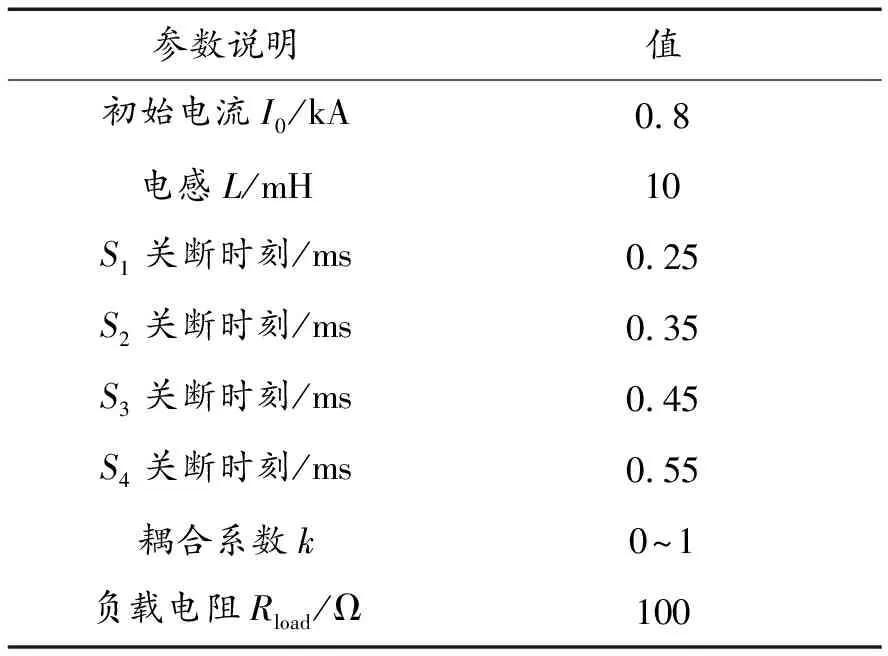
表1 仿真参数设置

采用直流恒压电源对电感进行充电，当电流达到初始电流800 A时，充电回路开关Sop断开，以此时刻作为零时刻，之后按照表1中的时序，S1～S4依次断开，S4断开的同时接通负载Rload，此时电路转变为一阶RL电路。

图6显示，在Si断开至Si+1断开时间内，电流几乎不会衰减，这是因为在晶闸管D接通之前，电路中没有负载，且开关触发间隔很短，仅存在微小的线缆电阻消耗电能；当负载Rload接通后，电流迅速下降，曲线符合一阶RL放电曲线。同时可观察到，在每一级开关关断时，电流均有较大幅度上升，且耦合系数k越大，电流提升的幅度越大，这与理论上的分析保持一致，图7显示仿真结果和构建的数学模型计算结果完全吻合。

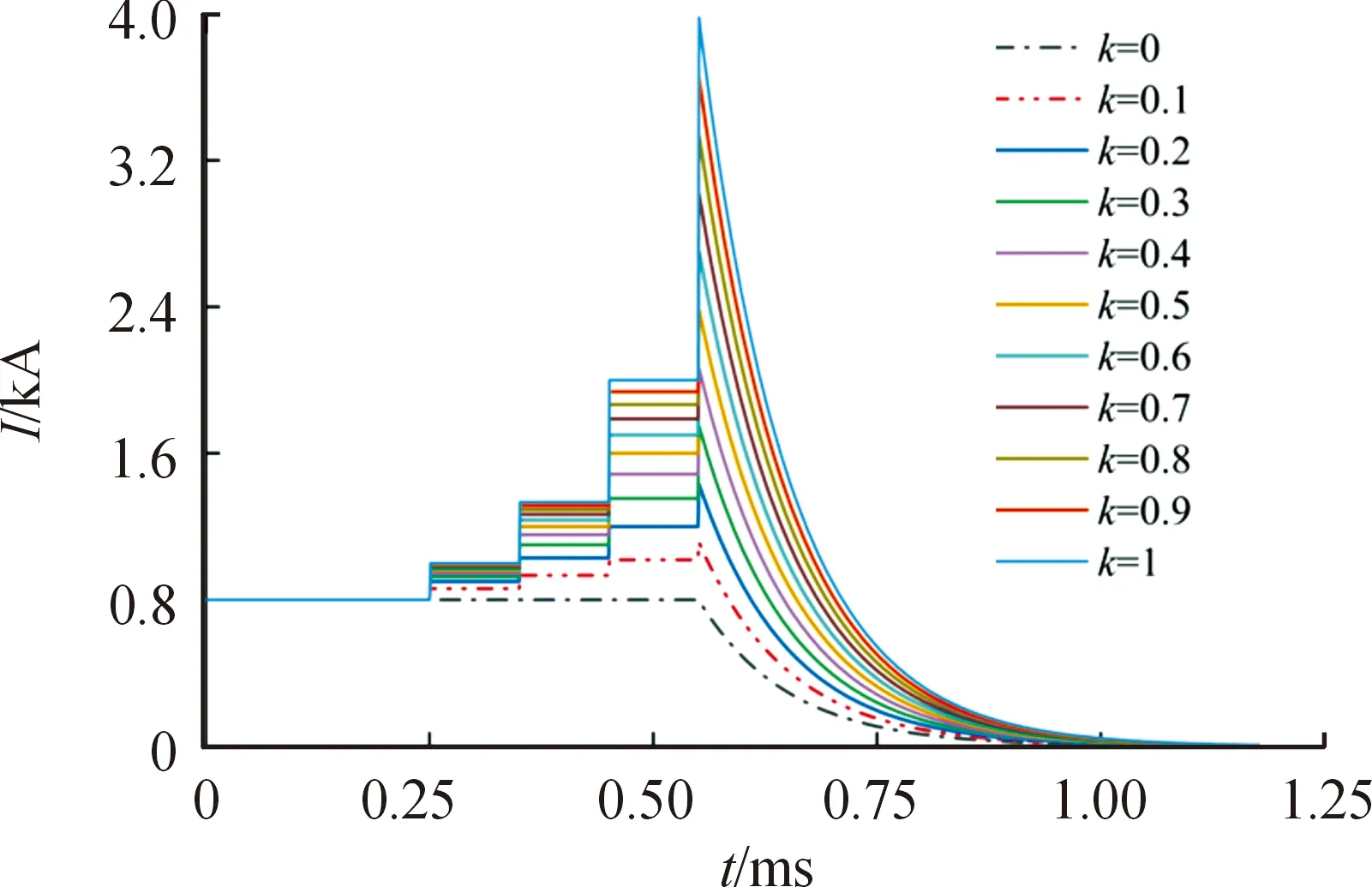
图6 5级耦合Meat Grinder输出电流仿真

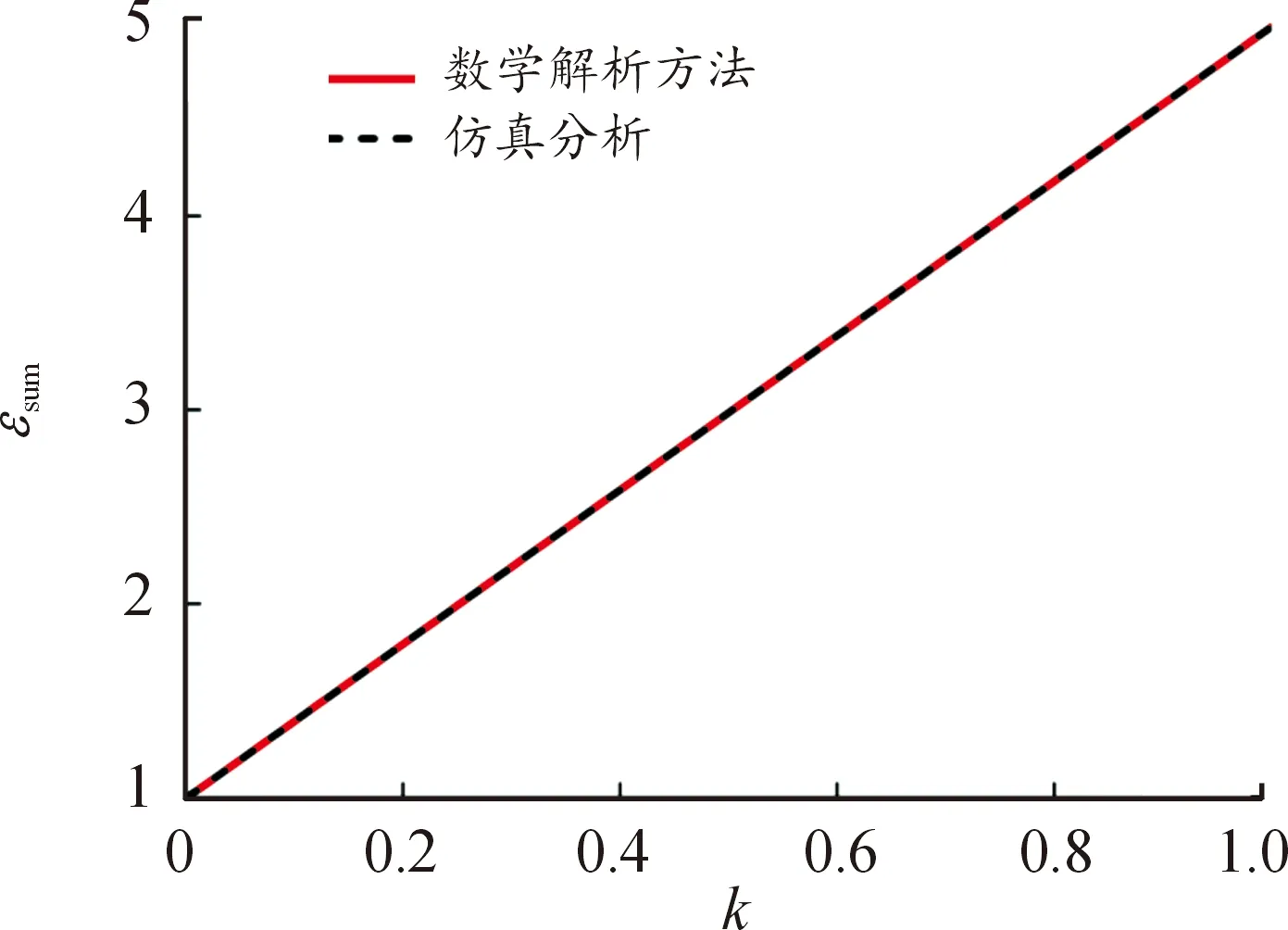
图7 数学解析方法与仿真结果的比较

4 单级耦合及多级耦合的Meat Grinder工程应用分析

n级Meat Grinder每次电流倍增都对应一次开关断开动作，由第一部分的电路等效模型可知，在理想状态下，流经关断开关的电流会在极短时间内衰减为零。然而实际应用中，开关可靠关断电流的能力具有一定限度，当关断电流过大时，开关会承受很强的电压应力，导致开关受损，这也是目前制约Meat Grinder电路应用的主要因素。美国Sitzman等提出引入辅助电容降低开关电压的方法，最终由于器件限制，最大可关断电流提高至4 kA[14]。德法联合实验室Dedie等采用逆流换路技术，实现了28 kA强电流的可靠关断[15]。

然而，对于n级Meat Grinder中的每一级电感，都需要一个大电流断路开关，随着电流增大，开关的关断难度越来越高，最后一个开关的关断电流最高将达到最终需求强电流的一半。若采用上述方法克服强电流关断的问题，无疑使电路结构更加复杂，因此需要考虑更为简便的方法，文献[11-20]均采用单级耦合的方式实现电流放大，但在理论分析方面有所欠缺，特别是在和多级Meat Grinder性能的比较方面，缺乏相关的研究。

通过前面的分析可知，单级耦合Meat Grinder的电流放大倍数计算公式为：

(14)

假设单级耦合Meat Grinder电感之间的耦合系数与多级耦合每两级电感之间的耦合系数k相等，且初级线圈电感与次级线圈电感的比为r，则电流放大倍数的公式可写为：

(15)

从式(15)可以看出，电流放大倍数ε受耦合系数k和电感比r的影响，在k固定且不为零的情况下，提升r的值，可以达到和n级Meat Grinder一样的电流放大效果。对式(11)(15)进行联立：

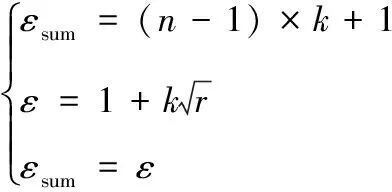
(16)

得到

r=(n-1)2

(17)

在耦合系数相同的情况下，若单级耦合电路的初级线圈与次级线圈电感值之比r满足式(17)，则其电流放大效果与n级Meat Grinder的相同。

利用simplorer仿真软件对与5级Meat Grinder电流放大效果等效的单级耦合电路进行仿真分析，同样以电流作为主要分析指标。

电路参数设置如表2所示。仿真实验结果如图8所示。

表2 对比仿真参数设置

通过对比图8和图6，当耦合系数k=0.2、0.4、0.6、0.8、1时，单级耦合电路与5级Meat grinder的电流放大效果均相同，最大可以从800 A放大至4 kA。下面对耦合系数等差为0.01时的单级耦合电路与5级Meatgrinder电流放大效果进行仿真分析，结果如图9所示。

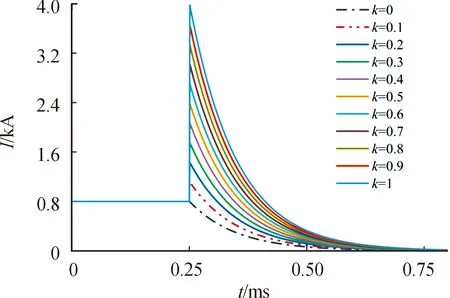
图8 单级耦合电路的输出电流仿真

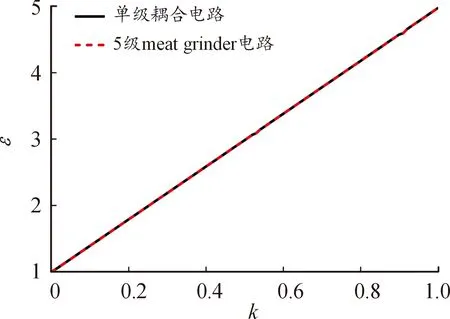
图9 5级Meat Grinder与单级耦合电路电流放大性能比较

从图9可以看出，利用搭建的单级耦合电路，在电流放大倍数方面，能够起到与多级Meat Grinder几乎完全一致的效果。然而，单级耦合电路仅进行了一次开关动作，只需完成800 A电流的关断，而多级Meat Grinder最高需要完成2 kA电流的关断，相比之下前者极大缓解了开关的关断压力。根据文献[6]中对电磁轨道炮电源技术的研究，驱动电磁轨道炮发射的电流通常在百千安级，如果采用上述2种电路对电磁轨道炮提供电流，则至少需要将种子电流放大数十倍以上，在这种情况下，单级耦合电路仍然只需克服种子电流的关断，而多级Meat Grinder最高面临几十千安的电流关断困难，而这在当前是无法解决的。

假设2种电路初始储能均为E0，电流放大效果相同的2种电路由于初始电感不同，因此初始电流也会有差异。基于此种情况，对2种电路的最终放大电流进行分析。设单级耦合电路初始电感为L01，n级MeatGrinder初始电感为L02，耦合系数均为k，2种电路初始电感可分别表示为：

L01=L+(n-1)2L+2kL(n-1)

(18)

L02=nL+n(n-1)kL

(19)

结合电感的储能公式E=0.5LI2与电流放大倍数计算式(11)，得到最终放大电流I1和I2的表达式：

(20)

(21)

利用Matlab软件进行数值计算，分别比较了n=2，4，6时的Meat Grinder电路和与其等效的单级耦合电路的电流放大效果，对比结果如图10所示。

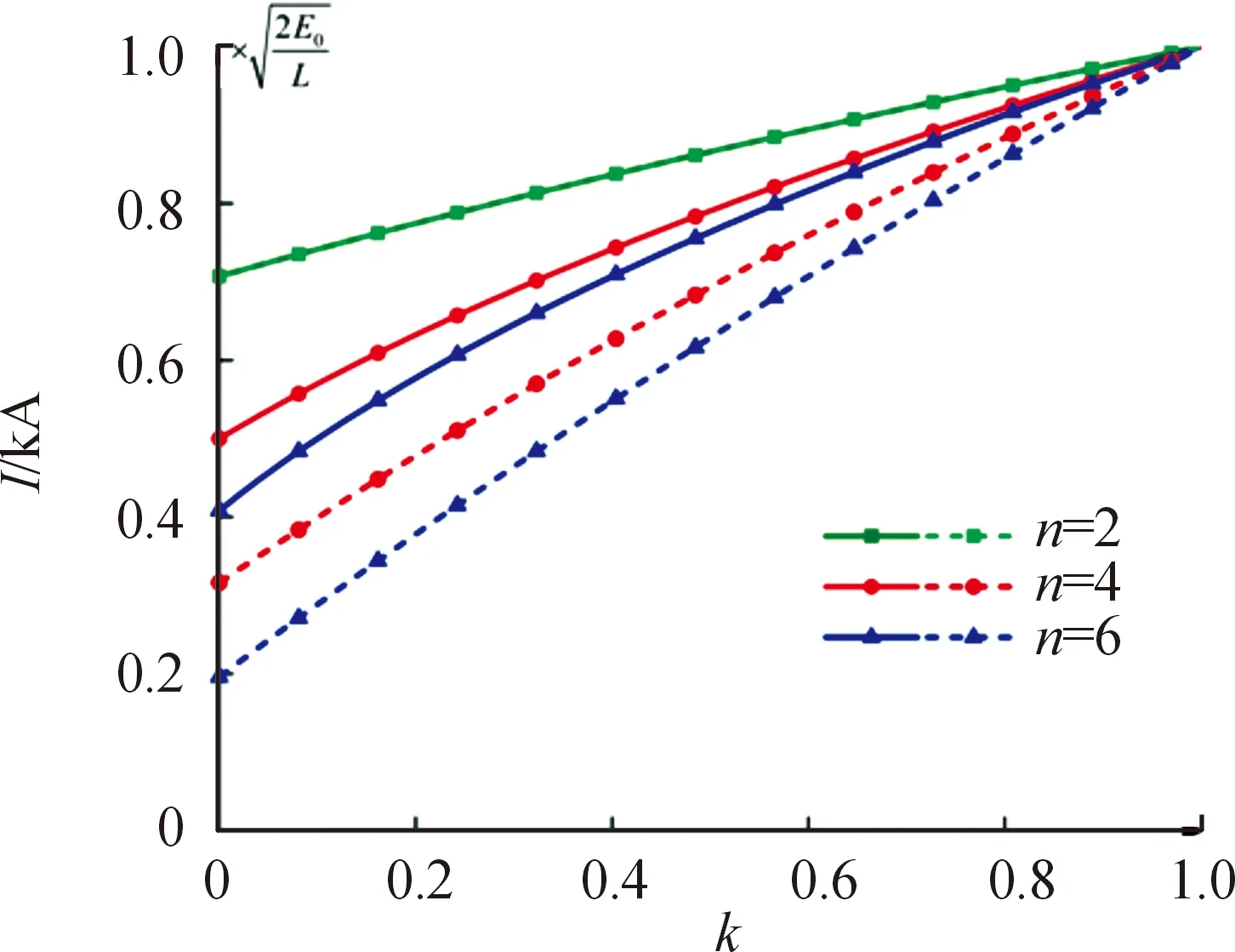
图10 初始储能相同时2种电路输出电流的比较

图10中使用了不同符号区分Meat Grinder的级数n，直线线型曲线为Meat Grinder，短横线线型曲线为与其等效的单级耦合电路，n=2时两条曲线重合。图10显示，当耦合系数相同时，单级耦合电路最终放大电流要小于n级Meat Grinder，随着耦合系数k不断增大，两者的最终的放大电流越来越接近。从物理意义上考虑，上述结论是在n级Meat Grinder各级电感线圈耦合系数k均相同的情况下的得出的结论，由于n级Meat Grinder的初始电感要小于单级耦合电路，因此初始电流更大，导致最终放大电流更大。在实际应用中，n级Meatgrinder各级电感线圈径向及轴向尺寸的不同必然会导致互感的差异，使平均耦合系数k难以达到较高水平；而单级耦合电路由于只具有两级电感线圈，通过适当地调整尺寸参数，使初级电感与次级电感紧密耦合，耦合系数k更易提高。因此可认为初始储能相同时，2种电路在最终输出电流方面并无太大差异。

从工程应用的角度考虑，单级耦合电路的设计难度更低，只需要一个大电流断路开关即可完成电流放大功能；使用起来更加方便灵活，降低初始电流I0的同时扩大电感比，既能够降低开关关断难度，也可以得到较大的放电电流；由于只有两级电感，因此耦合系数的设计相较于多级Meat Grinder要更加可控，制造难度更低。

5 结论

基于电磁耦合原理，对多级Meat Grinder电路输出性能进行了理论推导并开展了仿真实验，并针对多级Meat Grinder实际应用过程中大电流关断困难的问题，提出了等效单级耦合电路改进方案。研究结论如下：

1)耦合系数k是Meat Grinder电路输出性能的决定性因素，在电感级数一定的条件下，耦合系数越大，电流放大倍数ε越大，能量转换效率η越高。

2)通过增强级间耦合，单级耦合电路可达到多级meatgrinder电路相同的电路性能，且单级耦合电路在开关数量、动作时间等方面具有优势，于工程应用更易实现。