基于田口法的感应点火系统中线圈参数优化分析

王永艳，解志坚，杨 臻，黎 强，刘双庆

(1.中北大学，太原 030051；2.四川华川工业有限公司，成都 610100)

1 引言

电磁感应底火是一种利用无线能量传输技术实现点火的新型电底火，通过电磁感应原理，将电能从发射线圈传递到接受线圈，发射线圈和接收线圈间无机械连接，使得这种供电方式具有非接触、无机械摩擦、可靠性高等优势[1]。常规电底火由于工作环境恶劣，击针等部件因磨损、脏污等原因可能导致偶发接触或断路、接触不良的情况，不能有效击发电底火，直接影响武器效能[2-3]。使用感应底火，能够实现非接触点火，减少常规电底火的接触和磨损过程，同时避免因环境因素造成的短路、断路以及接触不良等问题，能够有效提高点火可靠性。

电磁感应无线能量传输技术在医疗、工业、兵器等领域应用广泛，如何提高无线能量传输效率是各研究领域面临的共同难题[4-6]。由于枪械身管、底火的结构特殊性，对无线传输电路发射、接受线圈的种类和大小限制较大。为保证感应点火能量，针对单一结构、在一定范围尺寸线圈间提高无线能量传输效率是本文中研究重点。文献[7-9]对线圈偏移角度对无线电能传输特性的影响做了具体分析，并利用Maxwell软件分析了线圈形状对耦合系数的影响，提出了耦合线圈的优化设计方案，对非接触式电能传输系统功率及效率影响因素进行了具体分析，得出了相关结论；文献[10]提出了一套线圈优化设计方案，并通过仿真分析验证了该方案的有效性和正确性。上述文献分别对线圈偏移角度、线圈形状和实际误差以及盘式线圈具体线圈参数对感应传输效率的影响进行了分析，但尚未对螺旋线圈初、次级线圈不相同情况下，各自线圈参数对能量传输效率的影响进行系统性研究。

本文中在XX项目的基础上开展了感应点火无线能量传输效率研究，建立了感应点火的数学模型和Maxwell同轴螺线管型线圈模型，采用单一变量法，取初、次级线圈参数如匝数、高度、半径等不同情况下，利用田口法建立直角表，分别对螺线管线圈互感进行仿真计算，并通过实验验证仿真计算正确性。基于仿真计算结果分析各参数对感应点火能量传输效率的影响情况，研究提高感应点火传输效率、提升感应底火工作可靠性的有效途径。

2 感应底火电能传输模型

感应底火初、次级线圈之间的传输效率受内部结构的影响较大，有针对性地进行改进，可以很大程度上提升电能的传输效率。接收端的并联谐振，适合给负载电阻进行充电，发射端串联谐振，可以降低系统对电源电压额定值的要求，故选择串并式模型(Series-Parallel)进行分析[11-14]。建立感应底火电能传输模型的谐振电路如图1所示。

图1中，U为输入电源，R1、R2为等效电阻，电阻大小相同，L1、L2为等效电感，M为L1、L2之间的互感，R3为负载电阻，Rs为电源内阻可以忽略。

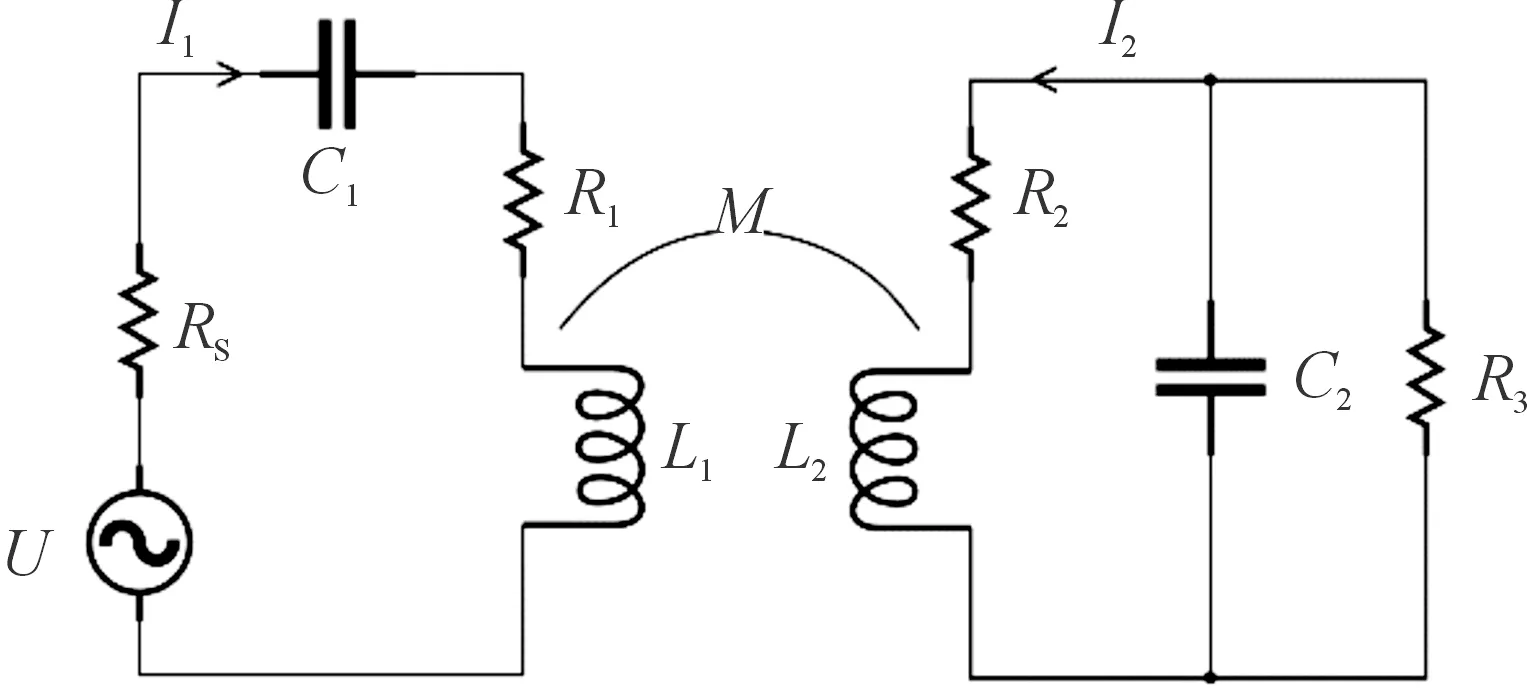
图1 电能传输模型电路图

原边电路和副边电路的等效阻抗Z1、Z2分别如式(1)和式(2)所示：

(1)

(2)

由于线圈之间存在互感，在初级侧和次级侧的互感电压分别为jωMI2和jωMI1。根据基尔霍夫电压定律可知回路的电压降总和为0，得：

(3)

(4)

由此可得谐振式无线电能传输系统的输入功率Pin、输出功率Pout和传输效率η：

(5)

(6)

(7)

如图2所示，将副边阻抗等效在原边电路中，Zeq1是副边回路在原边回路的反映阻抗。将原边阻抗等效在副边电路中，Zeq2是原边回路在副边回路的反映阻抗。在磁场中原、副边回路产生谐振，R1，R2为自感电阻非常小可以忽略。当系统发生谐振电路中感性和容性相互抵消，电路呈纯电阻特性。则原边电路和副边电路的等效阻抗Zin，Zout为

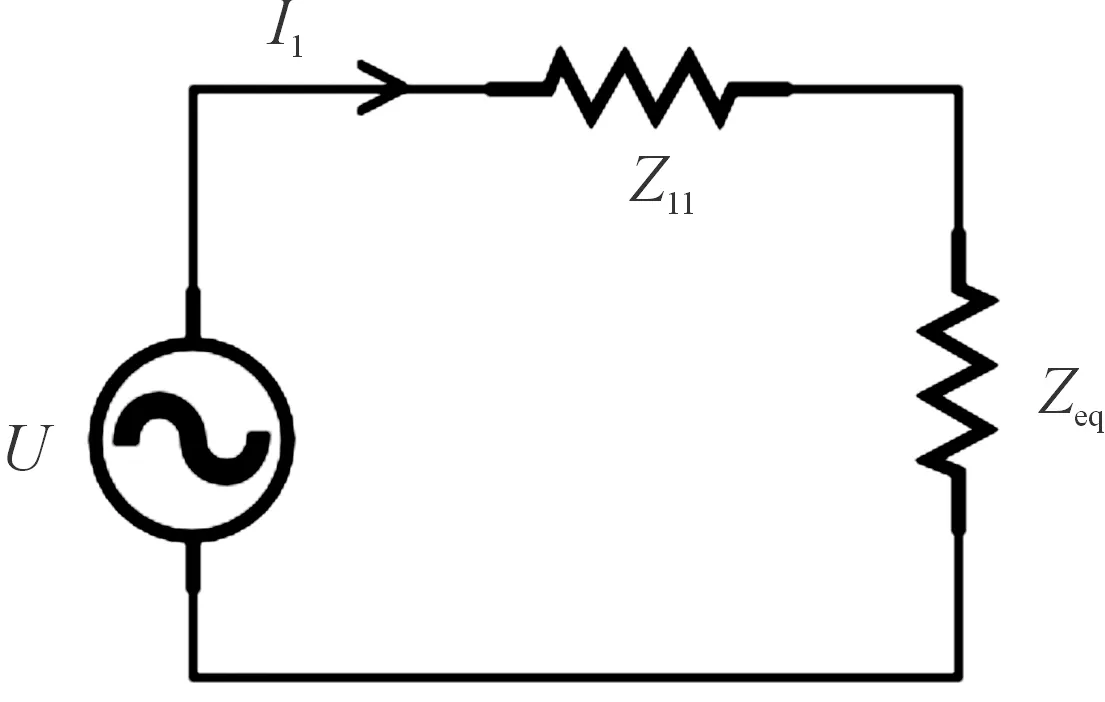
图2 等效电路图

(8)

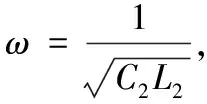
(9)

Zin=Z1+Zeq1

(10)

Zout=Z2+Zeq2

(11)

原边回路发生谐振时其阻抗Zin的虚部为零，化简可得：

(12)

(13)

将式(10)～式(15)代入式(8)、式(9)，可得谐振状态下输出功率Pout和传输效率η：

(14)

(15)

对于中等距离谐振耦合的无线输电系统，可忽略辐射损耗，线圈损耗电阻[15]

(16)

式中：μ0为真空磁导率，σ为电导率，a为导线半径，r为线圈半径，n为线圈匝数。

设线圈匝数6匝，线圈半径5 mm，导线半径0.4 mm的铜线圈，根据式(16)得欧姆损耗电阻为0.06 Ω，可见线圈损耗电阻很小，可以忽略。由式(15)可知，工作频率一定，负载电阻一定，存在一个互感M使得效率η存在最大值。

设初级线圈与次级线圈同心放置，如图3所示。互感计算公式为[14-16]：

(17)

(18)

(19)

H为螺线管的高度，D为线圈直径，角标1代表初级，角标2代表次级，D=2r，F1，F2为查表所得[18]。

由式(19)可知，存在一组参数，使得互感M达到最大，且互感M受匝数n，线圈高度H，线圈半径r的影响。

3 基于田口法的仿真分析

3.1 控制因子及干扰因子的选取

在田口算法中，选取对目标影响较大的参数作为控制因子[19]。本文中以获取最大传输效率为目标，以感应底火电能传输模型为基础，对控制因子进行选取。变量参数有初级匝数，次级匝数，初级线圈高度，次级线圈高度，初级线圈半径和次级线圈半径，由于线圈高度为匝数与螺距的乘积加上导线直径，匝数与导线半径对应高度，为简化计算，将控制因子线圈高度换为螺距。其余非控制因子对互感影响较小，可通过查阅相关材料选取合适的数值。为明确田口算法所优化的参数尺寸，图4对参数进行了重新定义，根据图3可知，控制因子对应图4的参数为A～F。

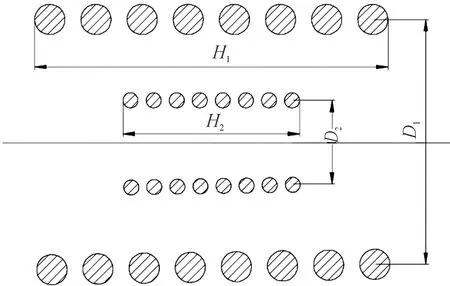
图3 初次级线圈剖面示意图

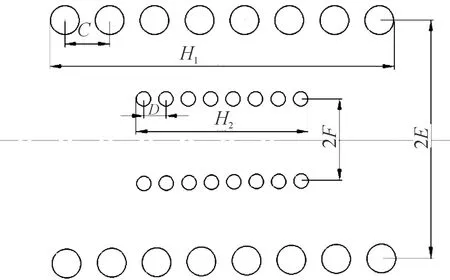
图4 控制因子示意图

根据不同控制因子组合，利用Maxwell软件进行仿真计算，仿真流程图如图5所示。

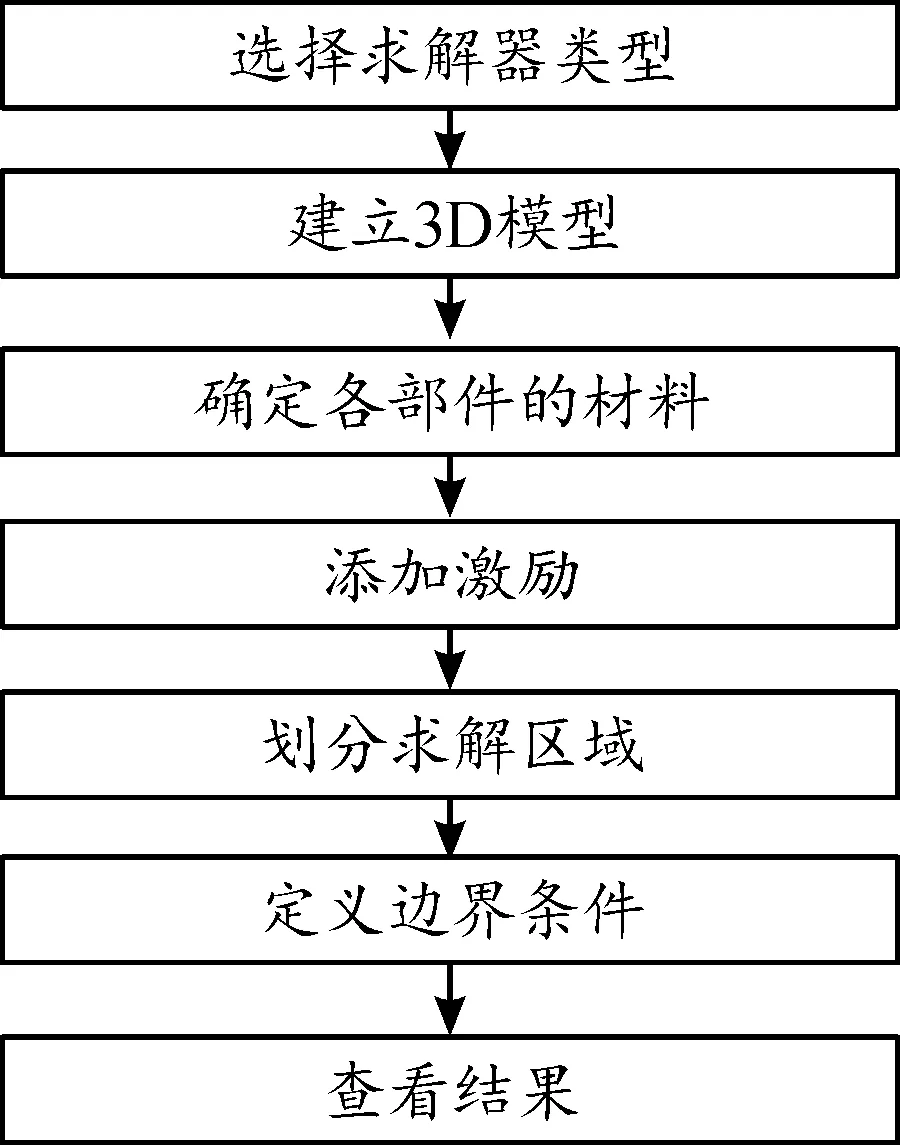
图5 仿真流程图

仿真计算时，求解器类型为涡流(Eddycurrent)，材料为铜(Copper)，初级线圈导线半径为1 mm,次级线圈导线半径为0.5 mm，两线圈为同轴螺线管，线圈为闭环设计，该仿真模型如图6所示。

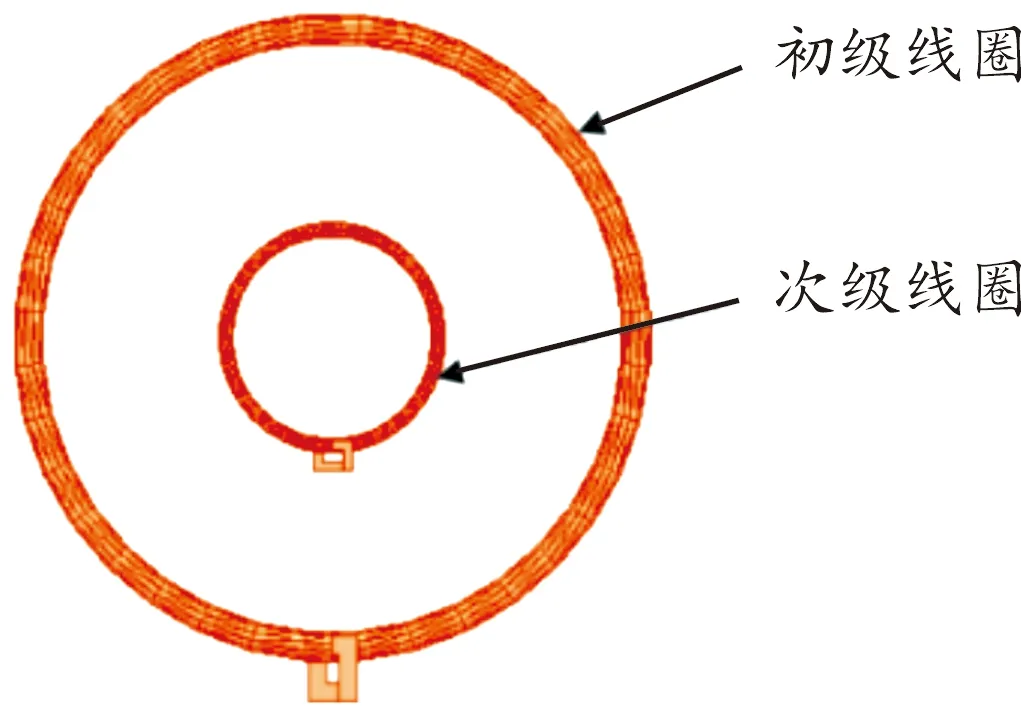
图6 仿真模型

初级线圈和次级线圈质心重合时磁通量最大[18]，当次级线圈沿线圈轴向发生移动时，穿过次级线圈的磁通量会产生变化，从而影响两者之间的互感大小。因此将次级线圈从质心重合位置沿线圈轴向的位移X选作噪声因子。六组控制因子及噪声因子的水平表如表1所示。

3.2 L25直角表的仿真分析

田口算法通过直角表设计实验并输入仿真计算结果，直角表中所有因子两两组合出现次数相同，全因子实验中，3个噪声因子、6个控制因子和5水平的组合需要15 625×3(56)次实验，使用田口法的正交试验表只需进行25×3次实验，具体直角表设计及对应有限元结果如表1所示。其中MX=i是表示X=i位置状态下，互感M在三组噪声因子下的仿真值, ηX = i是表示根据式(17)计算出对应的效率值。

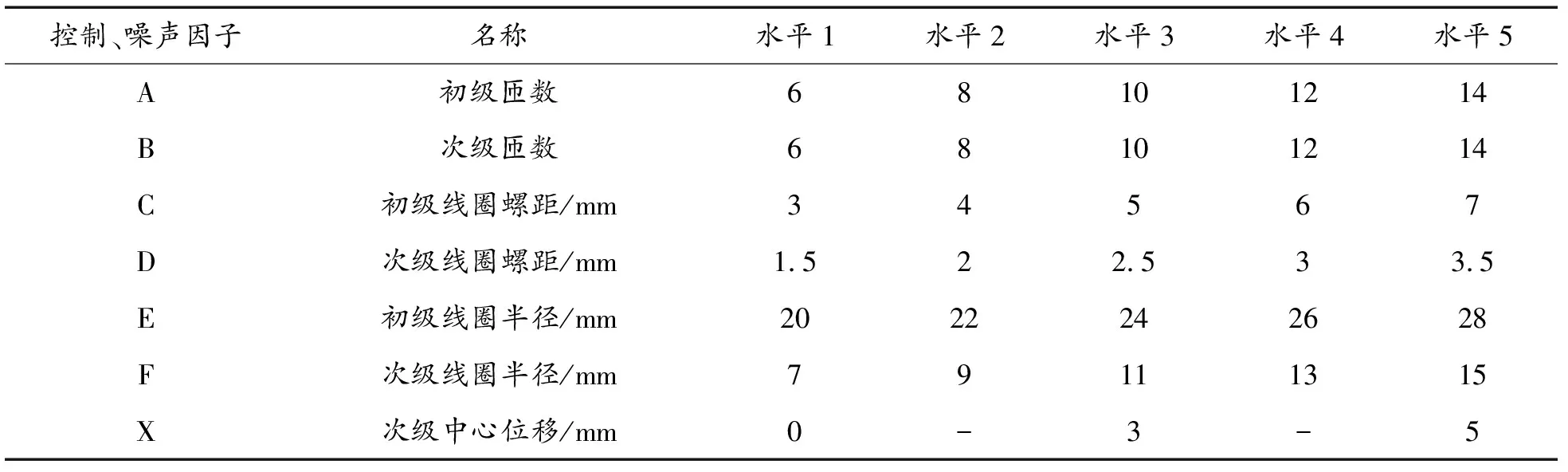
表1 控制因子及噪声因子的水平表

由于考虑了次级线圈沿轴向的位移X对互感的影响，因此使用信噪比对此影响进行定量表征，不同的组合对于噪声因子的抗干扰水平不一样。在田口法的工程实验中，对于效率的最优化设计属于望大特性研究，其信噪比计算公式为：

(20)

式中，n为总的次数，y为每次测得的互感值。

信噪比的大小表示了在设计过程中目标值受噪声因素干扰的程度。其值越大，目标值受噪声干扰影响越小[19]。利用Minitab对表2进行分析，得出信噪比主效应图，如图7所示。

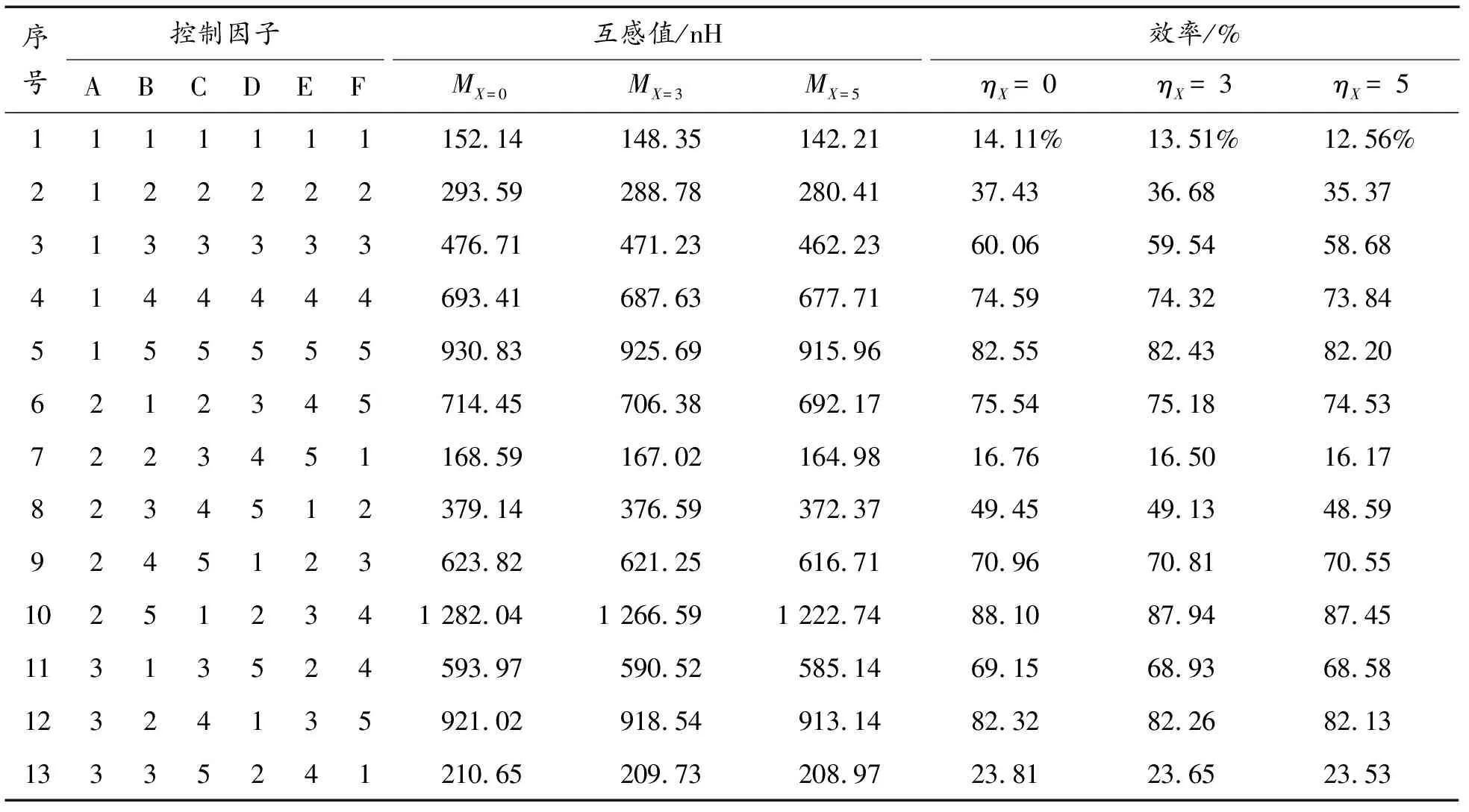
表2 L25直角表及仿真结果

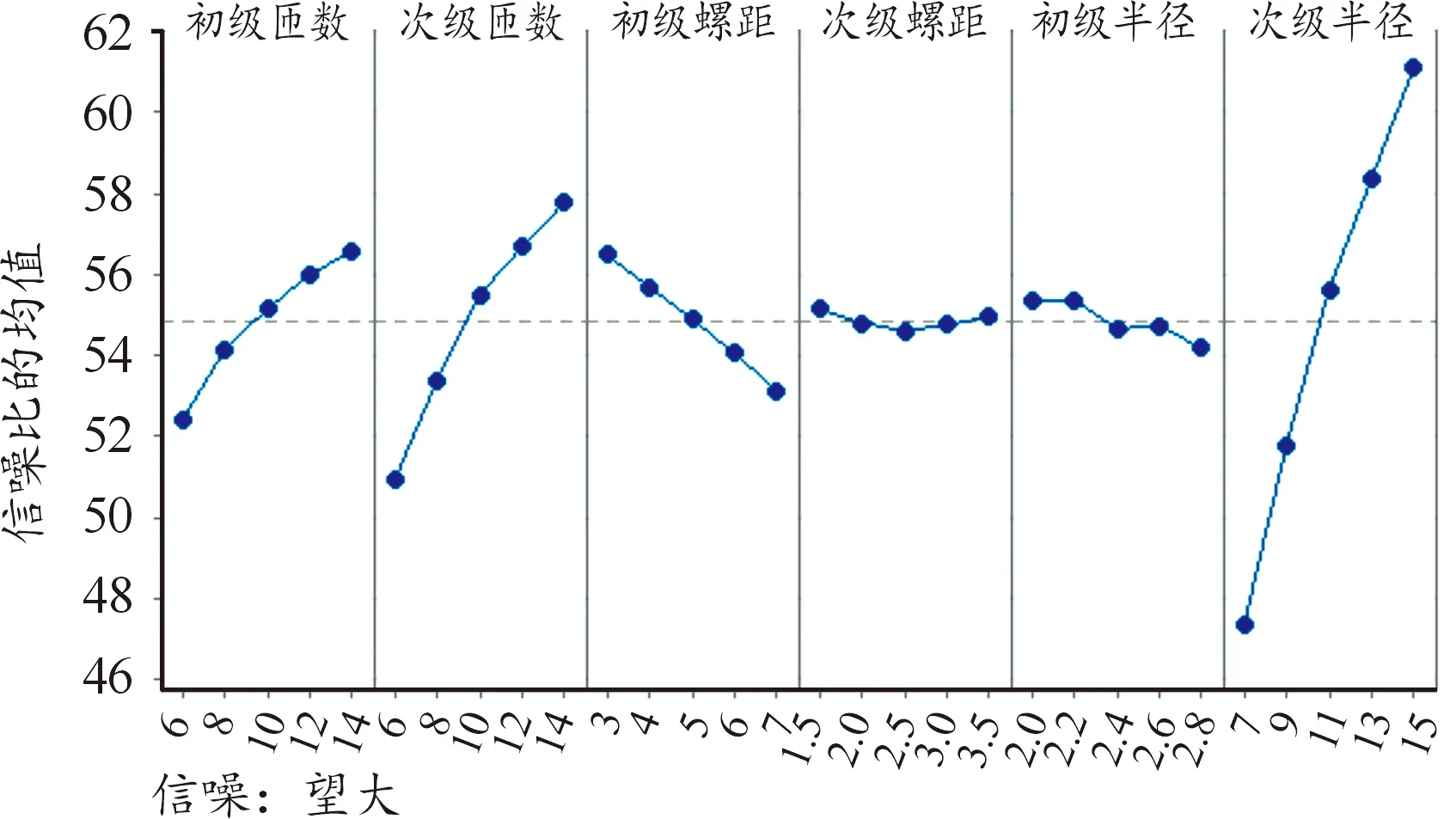
图7 信噪比主效应图

信噪比主效应图的效率大小表示影响程度,由图7可知，次级半径对互感的影响最大，次级匝数、初级匝数和初级螺距次之，初级半径和次级螺距影响最小。所以最佳影响组合为A5B5C1D1E1F5。经过田口优化后最终选取的参数及得出的互感值如表3所示。

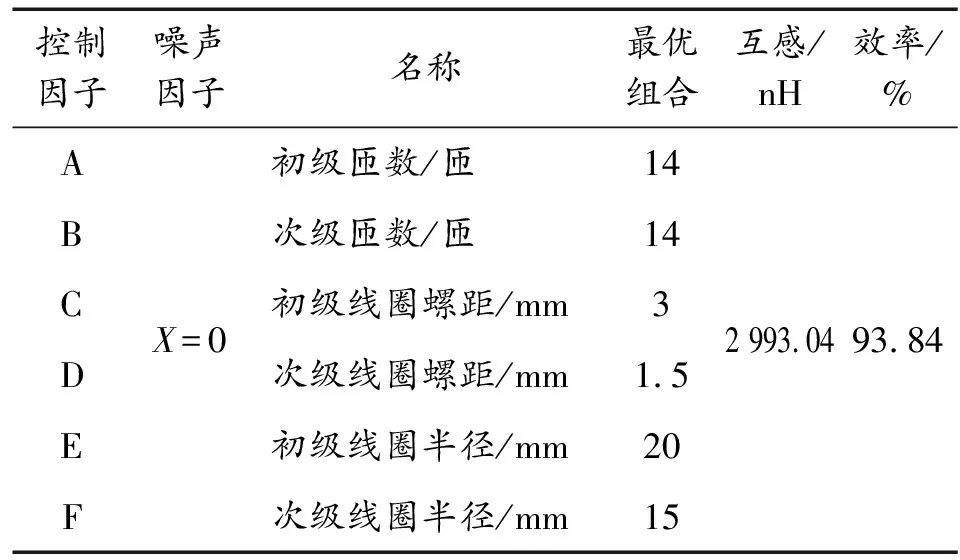
表3 优化后参数值与仿真结果

由最优结果可知，田口设计法选择的最优组合下，互感值是2 993.04 nH，代入式(15)，即可得出效率为93.84%。效率有效提高，证明该优化方案可行。

4 实验验证

当线圈结构一定时，自感值固定，两线圈相对位置确定，两者之间的互感值即为固定值。将初级线圈与次级线圈分别串接同名端与异名端，二者相减即为4倍的互感值。将数字电桥调为工作频率为100 kHz，线圈参数与表3一致。实验装置如图8所示，初次级线圈中心对正放置，使用TH2832测量互感值，所测互感值为3 014.78 nH，即可得出效率值为93.86%，与仿真结果具有较好的一致性,验证了仿真计算的正确性。

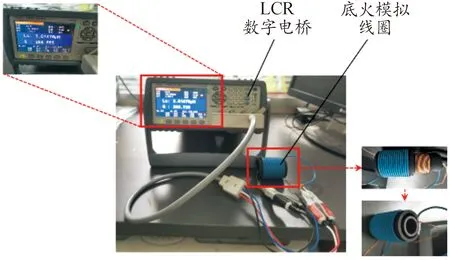
图8 模拟实验装置图

由于项目结构的限制，线圈半径不可减小，且螺距相较匝数的影响小，故选择匝数进行实验。实验将线圈直径、线径固定，调节匝数来得出不同匝数下初次级线圈的效率实验值。如图9所示。

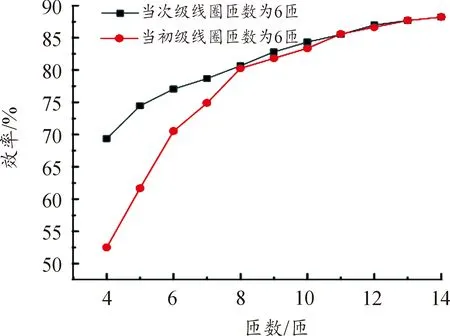
图9 匝数与效率试验图

由图9可知，次级线圈固定为6匝时，随着初级线圈匝数的增加，初次级线圈之间的效率逐渐增大；初级线圈固定时，随着次级线圈匝数的增加效率亦随之增大，与仿真分析所得趋势具有较好的一致性。

5 结论

本文对感应点火系统中各参数与能量传输效率间变化规律，以及不同参数对能量传输效率影响的强弱关系进行了数值模拟研究，并通过实验验证了仿真计算的正确性，研究结果表明：

1)感应点火能量传输效率与无线传输电路互感有关，互感值越大，效率越高，当互感值大到一定程度时效率趋近于1，增长速率明显降低；

2)感应底火中不同线圈参数对感应点火能量传输效率影响程度先后顺序为次级半径>次级匝数>初级匝数>初级螺距>初级半径>次级螺距；

3)考虑初次级线圈中心是否对正时，感应底火中最优线圈组合为次级半径15 mm，次级匝数14匝，初级匝数14匝，初级螺距3 mm，初级半径15 mm和次级螺距1.5 mm，优化后效率为93.84%。