例谈初中数学几何教学中发散性思维的培养

滕莉祥

［摘要］ 发散性思维是创造性思维的核心。在数学课堂中训练学生的发散性思维，是培养学生创造能力的关键。笔者在初中几何教学中通过训练学生思维的变通性、流畅性、联想性、广阔性来培养学生的发散性思维能力，从而让学生轻松地掌握数学知识间的内在联系，更好地认识和理解数学。

［关键词］ 创新能力；发散性思维；几何教学

一、转换思维角度，训练思维的变通性

发散性思维活动的展开需要突破学生固有的思维定式，从多方位及不同的角度去思考问题、解决问题。初中生的抽象思维正处于发展阶段，囿于固有思维方式，遇到新问题不能很好地转化和运用，因此教师要通过训练学生思维的灵活性和变通性来逐步培养和发展思维变通能力，使学生在数学课堂中逐渐形成具有多角度、全方位的思维视角和思维习惯。在执教苏教版八年级下册几何复习课时设计了这样一道题：

如图1，在正方形ABCD中，E，F分别是边AD，DC上的点，且AF⊥BE，求证：AF=BE。

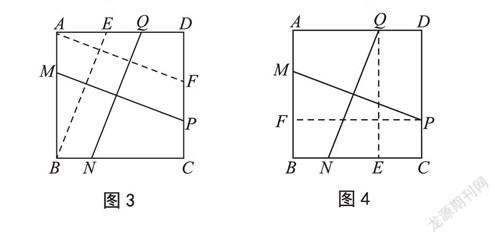
变式：如图2，在正方形ABCD中，M，N，P，Q分别是边AB，BC，CD，DA上的点，且MP⊥NQ。那么MP与NQ是否相等？并说明理由。

多数学生都可以快速地完成第一小问，因为这是通法。要证AF=BE，只需把这两条线段对应放到△DAF和△ABE中，通过寻找证明三角形全等的条件：∠BAE=∠ADF；∠ABE=∠DAF；AB=AD，证明△ABE≌△DAF即可解决。紧接着，在课堂教学过程中引出该题变式图2，保持垂直条件不变，使点M，P，N，Q与正方形的四个顶点不重合。此时，教师适时介入，学生们想到了多种方法：

法一：如图3，过点A作AF∥MP交CD于F，过点B作BE∥NQ交AD于E，通过平移线段将图2的问题转化为图1的问题，将未知问题转化为已解决的问题，充分利用转化的数学思想方法提升学生的变通能力。

法二：如图4，类比第一小题构造直角三角形，分别过Q作BC的垂线交BC于点E，过P作AB的垂线交AB于点F，类比图1转化为证明△NQE≌△MPF来解决。从解题优化的视角来分析，我们发现法一比法二更简洁方便。

二、一题多变，训练思维的流畅性

思维的流畅性是创造性思维的又一特征。在解决问题的过程中思维不受阻碍，能融会贯通，在较短的时间内选择恰当的方法解决问题。为了帮助学生实现这样的效果，在几何教学过程中反复进行一题多解、一题多变的训练，是行之有效的方法。在八年级下册第九章中心对称图形（第一课时）时设计的教学例题：

如图5，在四边形P中，点E，F在BD上且BE=DF，若四边形ABCD是平行四边形，求证：四边形AECF是平行四边形。

本题考查平行四边形的性质和判定，判定四边形AECF是平行四边形的方法有很多。法一：根据平行四边形的性质证明△ABE≌△CDF，得AE=FC，∠BEA=∠DFC，推出AE∥FC。利用AE平行且等于FC判定四边形AECF是平行四边形。法二：根据平行四边形性质证明△ABE≌△CDF和△ADF≌△CBE，从而推出AE=FC，AF=CE。利用两组对边分别相等的四边形是平行四边形判定。法三：由全等证明AE∥FC，AF∥CE判定平行四边形。法四：连接对角线AC，利用对角线AC，EF互相平分来判定。

在一题多解的教学过程中，教师要善于引导学生总结和提炼解题方法，优化方法寻找最优解。在接下来的教学过程中，笔者又继续设计了如下变式：

变式1：在四边形ABCD中，点E，F在BD上且BE=DF，若四边形AECF是平行四边形，则四边形ABCD是平行四边形吗？

变式2：如果在原条件基础上增加AB=AD，那么四边形AECF是什么图形？

变式3：在原条件基础上增加什么条件可使四边形AECF变成一个矩形？

变式1改变条件和结论继续巩固平行四边形的判定方法，深刻理解直接条件和间接条件间的相互转化，变式2和变式3通过强化条件巩固矩形和菱形的判定和性质，理解平行四边形、矩形、菱形间的内在联系。通过这样的变式训练，层层递进，环环相扣，紧紧围绕一个例题展开把平行四边形的性质和判定、矩形菱形的性质判定呈现出来，既巩固数学知识又锻炼思维能力，使学生思维流畅性得到发展。通过训练，让学生不断地探索解题的捷径，培养发散性思维能力。

三、善于联想，训练思维的联想性

联想思维是发散思维的显著标志。联想是发散的基础，培养学生善于联想的习惯是提升学生发散性思维的重要途径。通过广阔思维的训练，学生的思维可达到一定广度，通过联想思维的训练，学生的思维可达到一定深度。在联想的过程中，不断丰富学生的内在世界，提升思维水平。笔者就如何添加辅助线作如下教学尝试：

已知：如图6，AB=AE，BC=ED，AF是CD的垂直平分线，求证：∠B=∠E。

根据条件中的垂直平分线联想垂直平分线定理，自然连接AC，AD（如图7），得AC=AD，要证明∠B=∠E，只需证明△ABC≌△AED解决问题。突破这道题的关键是从已知条件垂直平分联想到与之相关的定理和知识点，本题中利用定理垂直平分线上的点到线段两端的距离相等。初中几何教学中需要培养学生联想与关联的思维，学生对数学定理及定理间的关联越熟悉，解题的效率就越高。

在几何教学中，教师可以基于某些特定的关键词激发学生的联想能力，如联想相关知识点、相关定理、联想相似的模型和图形，联想曾经见过的类似题目等。通过这样的联想训练，学生对所学内容有了整体把握，使所学的知识点形成一个结构体系，学会融会贯通、举一反三，促进创新思维的生长和发展。通过不断开发学生潜能，增强学生的发散思维意识。

四、基于单元整体强化条件，训练思维的广阔性

在数学课堂教学过程中，教师应重视从单元整体的视角训练学生的发散性思维。通过数学单元整体知识点间的系统联系和条件把握，以问题驱动促进学生的思维发展，强化和弱化某些条件，挖掘题目中条件和结论之间的关系来解决问题。丰富学生的数学思维，培养学生思维的严谨性和广阔性。笔者在执教苏科版八年级下册“中心对称图形”复习课（第二课时）设计了如下例题：

如图8，已知任意四边形ABCD，E，F分别为边AD，BC的中点，G，H分别为对角线BD，AC的中点，顺次连接E，G，F，H，判断四边形EGFH的形状。

仔细分析题干中给出的条件最突出的就是“中点”二字，在一个任意的四边形中存在多个中点，其指向性明确地引导我们要考虑使用三角形的中位线定理解决问题。该定理从数量和位置两个角度刻画两条线段的关系，在△DAB中，GE平行且等于AB；在△CAB中HF平行且等于AB，推出GE平行且等于HF，因此

证明四边形EGFH是平行四边形。接下来，我们通过强化条件关联整个单元的核心知识点。

强化条件1：当四边形ABCD具备什么条件时，四边形EGFH是菱形？关联点1：从平行四边形到菱形的路径有哪些？数量关系：一组邻边相等；位置关系：对角线互相垂直。根据已知条件，最后选择关联1中的数量关系解决问题。强化条件2：当四边形ABCD具备什么条件时，四邊形EGFH是矩形？关联点2：从平行四边形到矩形的路径有哪些？数量关系：对角线相等；位置关系：有一个角是直角。根据题目中的已知条件，选择关联2中的位置关系解决即当边AB与边CD是垂直关系时。强化条件3：当四边形ABCD具备什么条件，四边形EGFH是正方形？关联点3：从平行四边形到正方形、从矩形到正方形、从菱形到正方形的路径是什么？也可以理解为强化2与强化3的条件融合。

基于单元整体，强化条件，关联单元核心知识点，从数量关系和位置关系两种角度分析思维，始终做到前后一致，逻辑连贯，一以贯之，培养学生思维的严谨性和广阔性，提高学生的学习力和创造力。